Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-15 4/6/2004 17: 29 page 388

388 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

of two-dimensional landmarks. The main consequence of having an extra column is that

the computations are more tedious (especially for the programmer).

Below, we briefly review the operation (translation, scaling or rotation) that is per-

formed to superimpose configurations of two-dimensional landmarks, then present the

expanded form of the operation that applies to three-dimensional landmarks.

Centering

The first step of the superimposition is centering – translation of each configuration so

that its centroid is located at the origin of the coordinate space. In two dimensions, the

centroid (like the landmarks) has two original coordinates (X and Y). Each coordinate of

the centroid is the average of the corresponding coordinates of the landmarks. Centering

is accomplished by subtracting the coordinates of the centroid from the corresponding

coordinates of each landmark, yielding new centroid coordinates of (0, 0). To superimpose

three-dimensional configurations, we simply include the third (Z) coordinate in the same

series of calculations. Thus, the original coordinates of the centroid are the averages of the

corresponding coordinates of the landmarks:

+ X

+···+X

)

+ Y

+···+Y

)

+ Z

+···+Z

)(15.2)

To center the configuration we again subtract the values of the centroid coordinates from

the corresponding values of the landmark coordinates, but there are now three sets of

subtractions:

centered







−X

)(Y

−Y

)(Z

−Z

)

−X

)(Y

−Y

)(Z

−Z

)

−X

)(Y

−Y

)(Z

−Z

)

−X

)(Y

−Y

)(Z

−Z

)







(15.3)

When the operation is complete, the new coordinates of the centroid will be (0, 0, 0).

Scaling

The next step of the superimposition is scaling each centered configuration to unit centroid

size. In three dimensions, as in two, centroid size is defined as the square root of the sum of

the squared distances of the landmarks from the centroid. To compute the distance between

two points in three dimensions, we simply include the difference in the Z-coordinates along

with the differences in the X- and Y-coordinates:

D =



−X

)

+(Y

−Y

)

+(Z

−Z

)

(15.4)

Thus centroid size would be the square root of the sum of these squared distances. However,

after centering the configuration (X

=0), we can simplify the computation to

chap-15 4/6/2004 17: 29 page 389

BEYOND TWO-DIMENSIONAL CONFIGURATIONS OF LANDMARKS 389

the square root of the sum of the squared coordinates:

CS =









i=1

(15.5)

Then, to rescale the entire configuration to a centroid size of one, every coordinate in

centered

is divided by CS.

Rotation

As in the two-dimensional case, we are going to rotate the three-dimensional configuration

to the orientation that minimizes its partial Procrustes distance from a reference. At first

glance this might seem to be a simple extension of what we have done before – we just

include the third dimension in the calculations of the partial Procrustes distance and the

angle that minimizes that distance. As explained in Chapter 4 (Equation 4.12), the partial

Procrustes distance between two-dimensional configurations of K landmarks is:



j=1

−(X

cos θ −Y

sin θ))

+(Y

−(X

sin θ +Y

cos θ))

(15.6)

in which the coordinates of the target (X

, Y

) are related to the coordinates of the

reference (X

, Y

) by the angle θ. On closer inspection the problem turns out to be a

little more complex than just adding the difference in Z-coordinates to Equation 15.6,

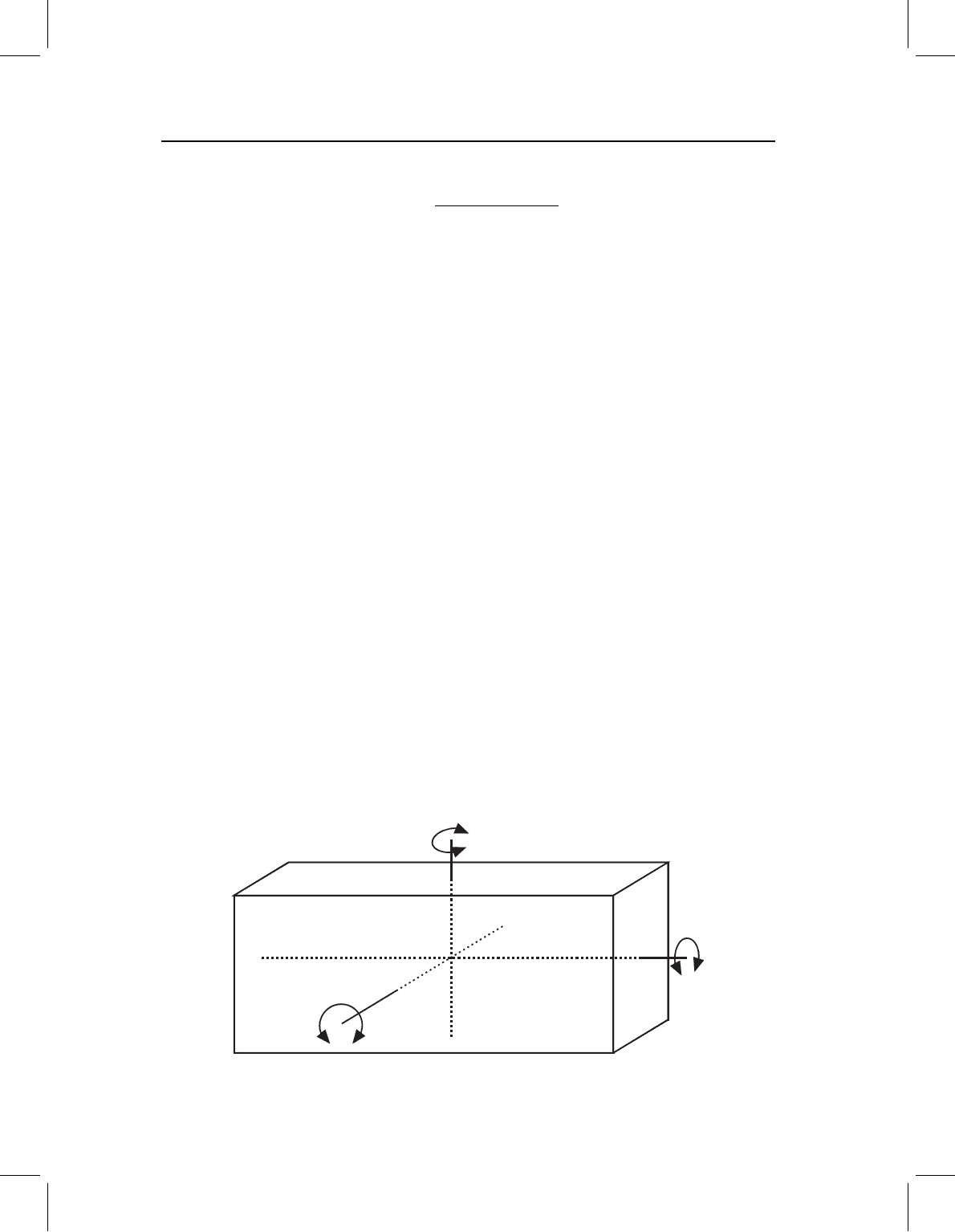
due to the fact that a three-dimensional object like the marmot skull can be rotated on

three orthogonal axes (Figure 15.2). This means there are three angles involved in the

computation of the partial Procrustes distance, and we have to solve for the particular

combination of angles that minimizes that distance. Still, the solution remains conceptually

simple, a singular value decomposition (SVD) of the matrix X

in which X

and X

are the centered and scaled configuration matrices of the reference and target, respectively

(Rohlf, 1990). As Rohlf points out, this is just one example of the general utility of SVD

for finding the angular relationship between two matrices.

Figure 15.2 Three orthogonal axes of rotation for a three-dimensional shape.

chap-15 4/6/2004 17: 29 page 390

390 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

The spaces of three-dimensional configurations

As discussed in Chapter 4, the set of all possible configurations of K landmarks with M

coordinates is called a configuration space, and this space has K ×M dimensions. Center-

ing, scaling and rotating to a specific alignment all select subspaces with fewer dimensions.

Because the same operations were used to select these subspaces, the same formulae can

be used to determine their dimensions. Centering removes M dimensions because the cen-

troid has M coordinates, so the space of centered coordinates has KM – M dimensions,

which is 3K −3 when M =3. Scaling removes one dimension because we are still using

centroid size, which is a one-dimensional scalar. Consequently, the space of centered and

scaled configurations (pre-shapes) has KM – M −1 dimensions (Equation 4.9), which is

3K −4 when M =3. Rotation to a standard orientation removes M(M −1)/2 dimensions

(Equation 4.10), which are the number of orthogonal axes on which an M-dimensional

configuration can be rotated. When M =3 there are three axes, and the space of aligned

configurations (a shape space) has 3K −7 dimensions.

When we impose on two-dimensional configurations of landmarks (K ×2 matrices) the

requirements of centering at the origin and scaling to unit centroid size, we generate a

pre-shape space that has the form of the surface of a hypersphere with a radius of one,

centered on the origin. When we impose the same requirements on three-dimensional

configurations, we again get a pre-shape space that is the surface of a hypersphere with

a radius of one, centered on the origin. Pre-shape spaces generated by these operations

have the same general shape (differing only in the number of dimensions), regardless of

the values of K and M.

The pre-shape spaces described above contain every possible rotation of every possible

M-dimensional shape that can be formed of K landmarks. Each shape is represented by the

set of all possible rotations of that shape, and the distance between shapes is the minimum

distance between these sets. As mentioned in Chapter 4, the set of all possible rotations of a

shape is called a fiber. This name seems apt when M =2; there is only one axis of rotation,

so we can visualize a one-dimensional string lying in the pre-shape space. When M =3,

calling the set of rotations a fiber may seem less appropriate because there are now three

orthogonal axes of rotation, which does not fit our mental image of a one-dimensional

string. However, the actual concept is still the same (the set of all possible rotations), and

it is just as useful. Because different fibers represent different shapes, they do not intersect;

and if they do not intersect, we can find the shortest distance between them. That distance

is the difference between centered and rescaled configurations that is not due to the rotation

of one relative to the other. Therefore, regardless of the values of K and M, the distance

between two shapes in the same pre-shape space is the distance between two points on the

surface of a hypersphere. Now that we are again on (relatively) familiar ground, we can see

that we must solve for the rotation of the target that minimizes the partial Procrustes dis-

tance (the chord length), which can then be converted to the Procrustes distance (arc length)

or the full Procrustes distance (the cosine of the angle subtended by the arc). Having a third

set of coordinates makes the computation more tedious, but the procedure is the same.

The shape spaces we generate by the operations described above are hyperspheres tan-

gent to their respective pre-shape spaces at the location of the reference shape. If centroid

size is fixed at one, the space is the surface of a hypersphere of radius one. If centroid size

is scaled to the cosine of the Procrustes distance, the space is Kendall’s shape space, the

surface of a hypersphere of radius one-half.

chap-15 4/6/2004 17: 29 page 391

BEYOND TWO-DIMENSIONAL CONFIGURATIONS OF LANDMARKS 391

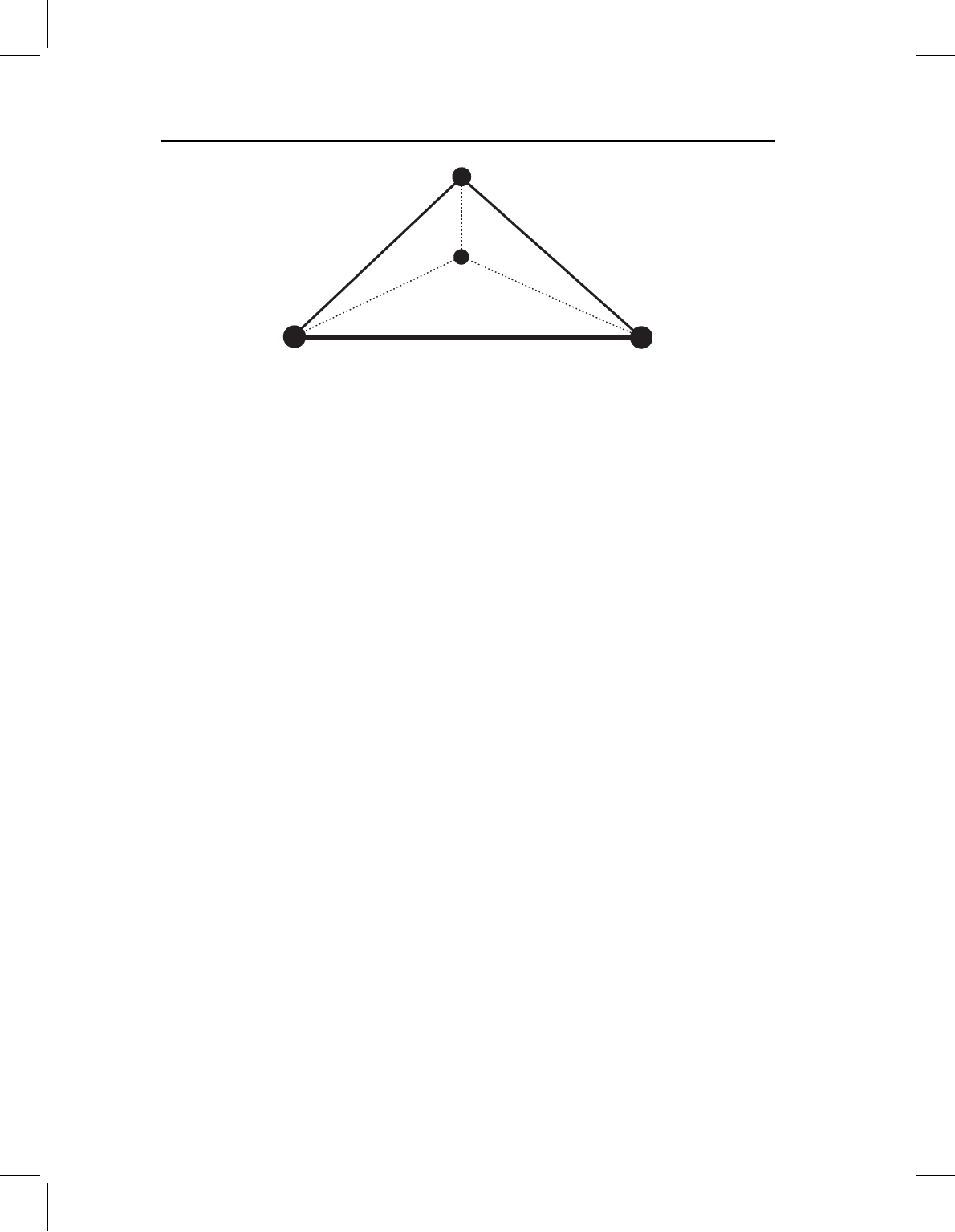
Figure 15.3 The simplest three-dimensional configuration of landmarks: a tetrahedron.

Decomposing the deformation

As in the two-dimensional case, the difference between three-dimensional configurations

of landmarks can be described as a deformation of one shape (reference) into the other

(target). This deformation can be decomposed into uniform and non-uniform parts (or

affine and non-affine). The non-uniform part can be further decomposed into 3(K −4)

independent components. The uniform part can be further decomposed into twelve

independent components; but only five of these change shape.

The numbers of uniform and non-uniform components can be explained if we consider

the possible deformations of the simplest three-dimensional shape, a tetrahedron of four

landmarks (Figure 15.3). All deformations of a tetrahedron, like all deformations of a

triangle, must be uniform; only when a fifth point is added can we detect non-uniform

transformations (i.e. transformations that differ between regions of the tetrahedron). With

just four landmarks a deformation can have twelve components, all of them uniform.

Seven of the uniform components do not change shape – they are the ones removed by

superimposition – which leaves five uniform components that do change shape. With each

additional landmark beyond the fourth, there are three possible non-uniform components

of deformation (because there are three directions in which that point might move relative

to the others), hence 3(K −4).

The components of the non-uniform part of a three-dimensional deformation are defined

in nearly the same terms as the components of the non-uniform part of a two-dimensional

deformation. Again, we use the thin-plate spline model to describe the deformation at

any point in space as f

, f

and f

, which describe the X-, Y- and Z-components of the

deformation:

(X, Y, Z) = A

X +A

Y +A

Z +



i=1

U(X −X

, Y − Y

, Z −Z

)

(X, Y, Z) = A

X +A

Y +A

Z +



i=1

U(X −X

, Y − Y

, Z −Z

)

(X, Y, Z) = A

X +A

Y +A

Z +



i=1

U(X −X

, Y − Y

, Z −Z

)

(15.7)

chap-15 4/6/2004 17: 29 page 392

392 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

where U(X −X

, Y −Y

, Z −Z

) is a function of the interlandmark distances given by:



(X −X

)

+(Y −Y

)

+(Z − Z

)

(15.8)

Again, we have more columns to accommodate the third dimension. The more substantive

difference is that U =R, in contrast to the two-dimensional case in which U =R

ln R

As in the two-dimensional case (see Chapter 6), the next steps are to solve for the spline

coefficients (the values of A and W) and the eigenvectors of the bending energy matrix (the

partial warps).

In both the two-dimensional and three-dimensional cases, the thin-plate spline is

only used to solve for the non-uniform components of the deformation; a different

approach is taken to solve for the uniform components. Bookstein (1996b) shows that

the approach he developed to construct a pair of basis vectors for the uniform part

of a two-dimensional deformation can be extended to the three-dimensional case. This

approach yields three pairs of vectors describing shear and compression/dilation in each

of the three two-dimensional planes (XY, YZ and XZ). But remember, there are only

five possible shape variables for the uniform part; therefore, the six vectors are not all

completely independent. In fact, the problem lies in the three compression/dilation vec-

tors; these three vectors actually describe a two-dimensional space. Bookstein suggests

several methods to rectify this problem by constructing an orthonormal basis for this

subspace (the current IMP software uses the Gram-Schmidt technique – cf. Axler 1996).

These two vectors, combined with the three shear vectors, provide an orthonormal basis

for the entire uniform subspace. More recently, Rohlf and Bookstein (2003) have pre-

sented two other methods, both using an SVD to compute an orthonormal basis for the

entire uniform subspace (without dividing it into shear and compression/dilation sub-

spaces). The methods differ in how they extract the uniform variation from the total

variation. In one, a technique used to compute residuals from a regression is used to

compute the uniform component as the residuals from the non-uniform (as the differ-

ence between the total deformation and the non-uniform part). In the other, a technique

used by Rohlf and Slice (1990) to compute the uniform component directly from super-

imposed two-dimensional coordinates is extended to three-dimensional coordinates. The

new methods differ from that proposed by Bookstein (1996b) only in the simplicity of the

algorithms; all lead to the same conclusions regarding the differences among populations

of shapes.

The result of the completed decomposition (of both uniform and non-uniform

components) is an orthonormal basis for the Euclidean space that is tangent to the

shape space at the location of the reference shape. Every configuration of land-

marks in a data set can be described as a deformation of the reference shape; and

that deformation is represented by the full set of scores on the five uniform compo-

nents and 3(K −4) non-uniform components. These scores preserve Procrustes distances

and express shape differences as scores on the same number of orthogonal axes as

there are dimensions of the shape space (which is equal to the number of statistical

degrees of freedom). Consequently, these scores can be used in standard multivariate

analyses.

chap-15 4/6/2004 17: 29 page 393

BEYOND TWO-DIMENSIONAL CONFIGURATIONS OF LANDMARKS 393

Ordinations and statistics

All of the analytic techniques discussed in Chapters 7–12 can be performed on data from

three-dimensional landmarks. This includes analyses performed on the partial Procrustes

distances of individual specimens from a reference shape (e.g. Goodall’s F-test) and anal-

yses performed on the full set of scores over all of the axes of the tangent space (e.g.

principal components analysis). None of these analyses is materially altered by the use of

three-dimensional coordinates. The transition from univariate to multivariate requires

changes in analytic tools, but after this transition has been made, no further methodolog-

ical changes are required to accommodate further increases in the number of variables.

The crucial thing to remember is that an analysis of three-dimensional shapes will have

more shape variables than an analysis of two-dimensional shapes with the same number

of landmarks. You will need larger sample sizes to perform comparable tests.

Illustrating shape differences

Although the mathematics of comparing three-dimensional shapes is well established, the

difficulties of illustrating those comparisons on static two-dimensional media (like the

pages of this book) have not been resolved to our satisfaction. The problem is not one of

illustrating a single, solid three-dimensional object–askilled artist or photographer can

produce very convincing two-dimensional images. Instead, the problem is that the process

of creating the illusion of three dimensions necessarily entails omission or distortion of

some information. For example, lengths and angles are distorted (by foreshortening) to

create the illusion of depth, and illustration of a fully rendered surface precludes illustration

of internal details or the other side of the object.

The problems of illustrating three-dimensional objects are exacerbated when the objects

are superimposed. If the surfaces are rendered, they will interpenetrate (i.e. only parts of

each will be shown – the parts that are “in front”); consequently, the viewer does not

see all of either object, and so cannot fully appreciate the shape difference. To illustrate

differences at all landmarks, the images of the objects must be simplified in some way.

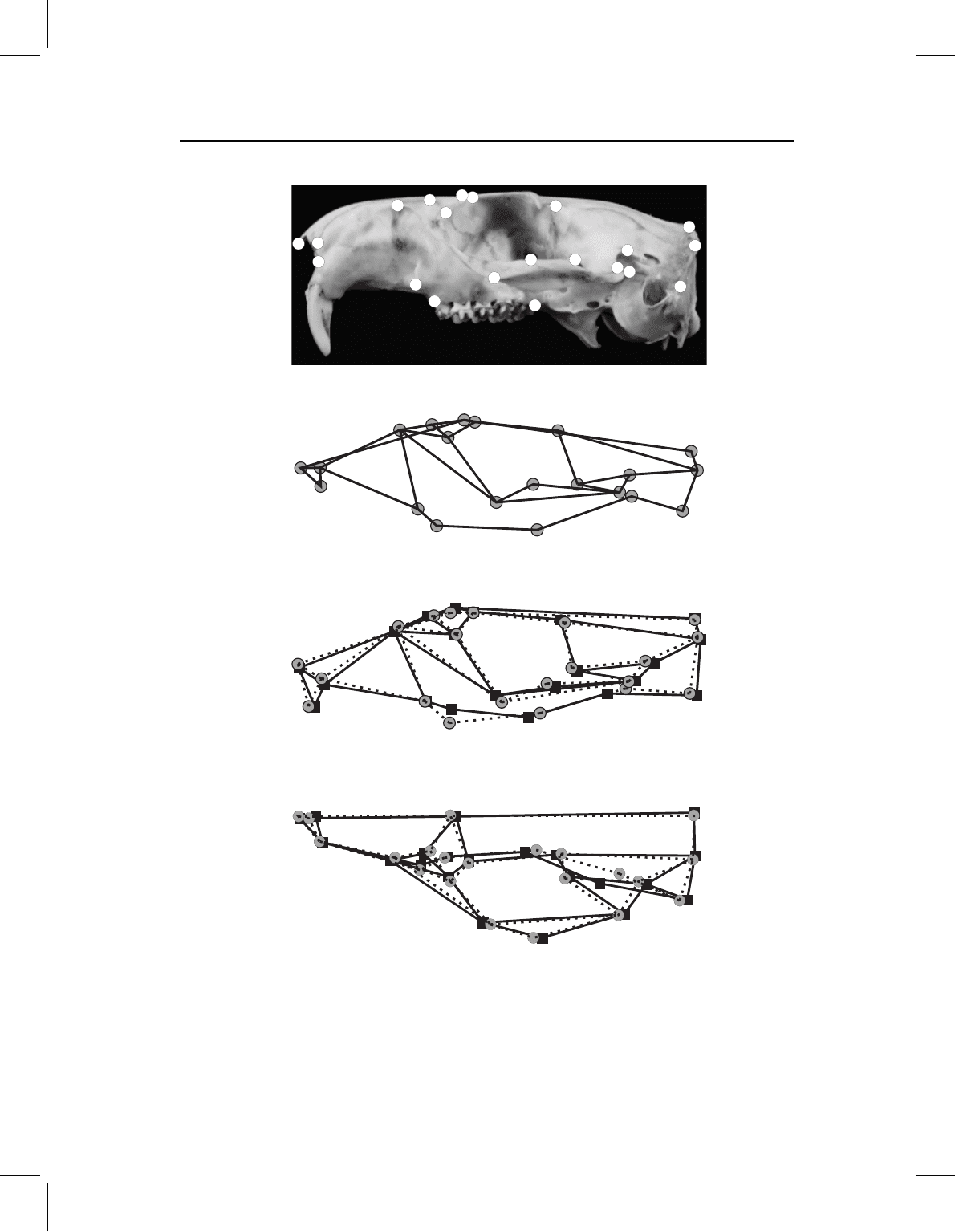
Figure 15.4A shows a photograph of a skull with a selection of landmarks. In Figure 15.4B,

the landmarks are projected onto the plane of the page and are connected by a wireframe,

a set of straight lines chosen to approximate salient features of the skull. With judicious

selection of line weights or colors, wireframes can be used to illustrate two superimposed

configurations of landmarks (Figure 15.4C), but even with the most lurid color scheme

a wireframe illustration of more than two configurations would be too confusing to be

useful. Furthermore, a single view of the wireframe cannot convey differences in depth; at

least one other view is needed, as in Figure 15.4D.

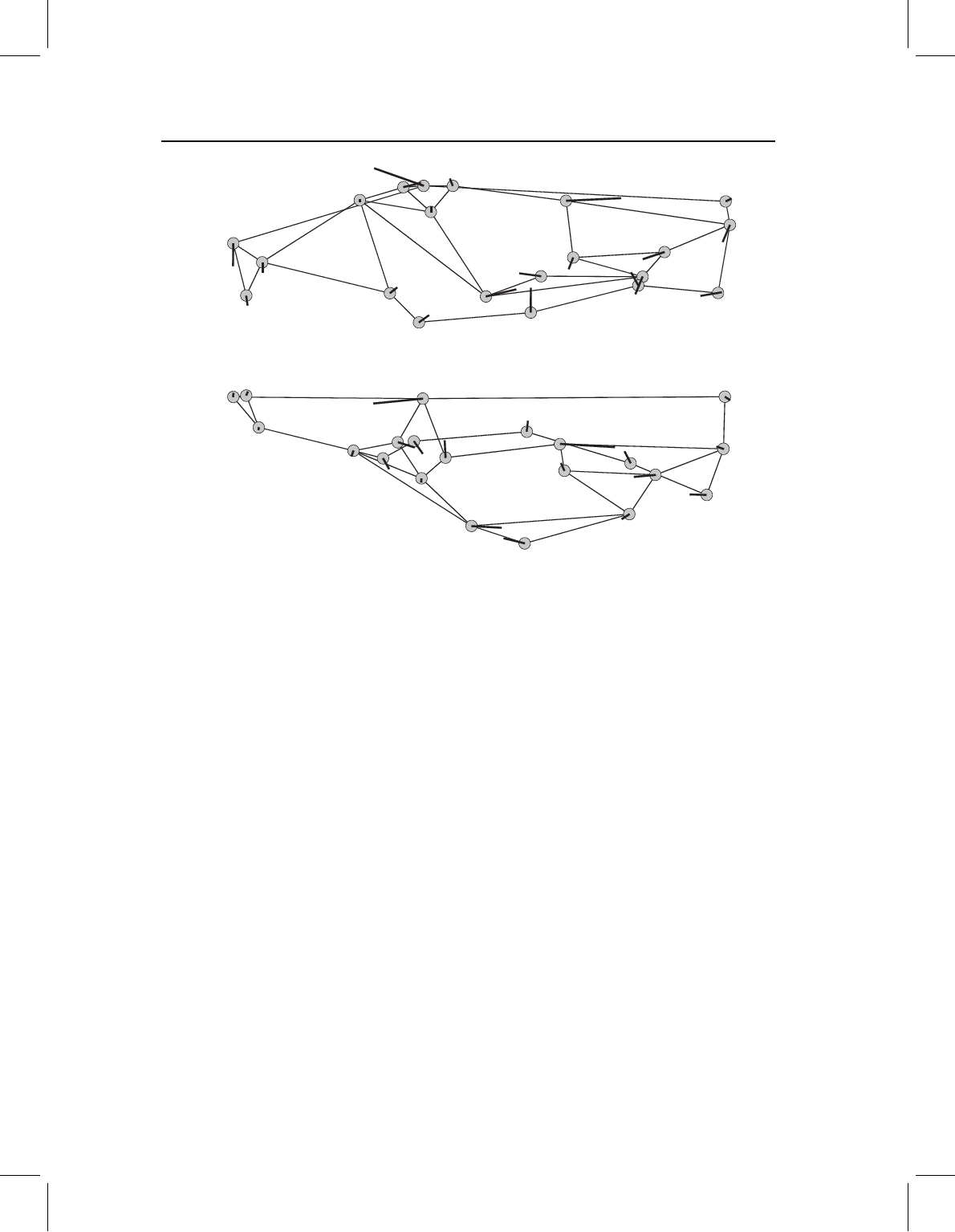
Illustrating a three-dimensional deformation on static two-dimensional media is even

more difficult than illustrating two superimposed objects. A variety of devices can be used

to draw the three-dimensional spline interpolation (e.g. the deformed grid or a series of

arrows on the nodes of an undeformed grid), but all have the same limitation – any dia-

gram displaying enough data to be useful contains too many data to be interpretable. The

simplest useful approach appears to be placing arrows on the wireframe of the reference

form (in two views) to indicate directions of relative landmark displacement (Figure 15.5).

Although this approach requires viewers to do the interpolation in their heads it does

chap-15 4/6/2004 17: 29 page 394

394 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

1213

(A)

(B)

(C)

(D)

Figure 15.4 Illustration of three-dimensional shapes using wireframes: (A) lateral view of a mar-

mot skull, with some possible landmarks; (B) the same landmarks in lateral view connected by a

wireframe; (C) two superimposed configurations and their wireframes, in lateral view; (D) the same

two configurations in dorsal view.

chap-15 4/6/2004 17: 29 page 395

BEYOND TWO-DIMENSIONAL CONFIGURATIONS OF LANDMARKS 395

(A)

(B)

Figure 15.5 Illustration of a deformation of a three-dimensional shape, using vectors at landmarks

connected by a wireframe: (A) lateral view; (B) dorsal view.

convey the localization of shape change, which may be the most important information

that can be gleaned from the spline.

Curves without landmarks

Many features of interest to biologists are curves that lack landmarks, such as short seg-

ments of edges or ridges between landmarks, or outlines encompassing whole organisms.

(Similar problems and methods apply to comparisons of three-dimensional surfaces like the

cranial vault, but for the sake of simplicity we return here to two-dimensional shapes.) The

lack of landmarks is a problem because the entire mathematical framework of geometric

morphometrics rests on the comparability of landmarks from specimen to specimen. With-

out comparable landmarks there is no justification for the Procrustes distance metric, or

for the superimpositions and shape spaces founded on that distance. Without landmarks,

we cannot apply the mathematical theory of shape spaces.

There are methods of analysis that do not require comparable points along the curve

of interest (Rohlf and Archie, 1984; Ferson et al., 1985; Lohman and Schweitzer, 1990;

MacLeod and Rose, 1993). In these approaches, points digitized along the curve serve only

as local estimates of the location of the curve. A function is fitted to the digitized points,

producing a set of coefficients representing the shape of that curve, and these coefficients

are used as variables in any subsequent comparative analysis. Although this appears to

be a clever way to circumvent the lack of landmarks, it is important to remember that

the configurations represented by the coefficients are not shapes as defined by Kendall.

chap-15 4/6/2004 17: 29 page 396

396 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

The configurations may have been aligned and scaled by precise and rigorous methods (cf.

Ferson et al., 1985), but a Procrustes superimposition is precluded by the lack of corre-

sponding points, and perhaps by the nature of the curve-fitting algorithm. Consequently,

the spaces occupied by these configurations are not the spaces covered by the theory of

geometric morphometrics. In addition, the descriptions of curves produced by these meth-

ods are incommensurate with descriptions of shapes based on configurations of landmarks.

This means that the coefficients of the curve-fitting function and shape variables computed

from Procrustes superimposed landmarks cannot be combined into a single shape analysis.

The best that can be done is to use PLS to look for correlations between the two sets of data.

Defining comparable points along a curve

To analyze curves in the same analytical framework as landmarks, and especially in a study

simultaneously with landmarks, we need a way to identify points on the curve that can

be treated as though they were landmarks. This means that we need to supply criteria for

recognizing or selecting points that are not specific to the region immediately surrounding

the curve (otherwise we would have landmarks). One such criterion would be to select

points that are at equal intervals along the curve (e.g. 10% of the length of the curve). In

Bookstein’s (1991) typology of landmarks, Type 3 encompasses points that are defined

by these sorts of extrinsic criteria. Subsequently, the term semilandmarks was used by

Bookstein (1997a, 1997b) to refer to a series of points that are located along a curve using

these kinds of criteria to define their positions along the curve. As Bookstein points out in

all three cited references, semilandmarks and similarly defined points do not have as many

degrees of freedom as the number of coordinates describing their location. The reduced

degrees of freedom are a consequence of defining the semilandmark in terms of its position

relative to other features. For example, a semilandmark defined to be halfway between the

ends of a curve that connects two landmarks can only tell us one thing about the curve that

we could not have inferred from the coordinates of the landmarks: the bowing of the curve

(i.e. the amplitude of its deviation from a straight line). Consequently, the semilandmark

has only one degree of freedom even though it has two coordinates.

There are a number of ways to delimit segments of the curve under analysis, and

Figure 15.6 shows three possibilities: by increments along the length of the curve (Fig-

ure 15.6A); by increments along the length of a chord connecting the ends of the curve

(Figure 15.6B); or by increments of an angle subtended by the curve (Figure 15.6C). In

addition, the increments might all be equal, or they might vary in a way that reflects the

complexity of the curve they are sampling. The combination of choices that produces the

most satisfactory sampling of the curve will depend on the geometry of the curve and its

relationship to other features represented by landmarks. This is not just a matter of aes-

thetics; the results of subsequent analyses can depend on the sampling of the curve, just as

the results of landmark-based studies can depend on the selection of landmarks.

Superimposing configurations with semilandmarks

Choosing a general approach to selecting semilandmarks is only one of the decisions that

must be made. Because semilandmarks are not locally defined and have reduced degrees

of freedom, users must also decide how to adjust several steps in the analysis of shape

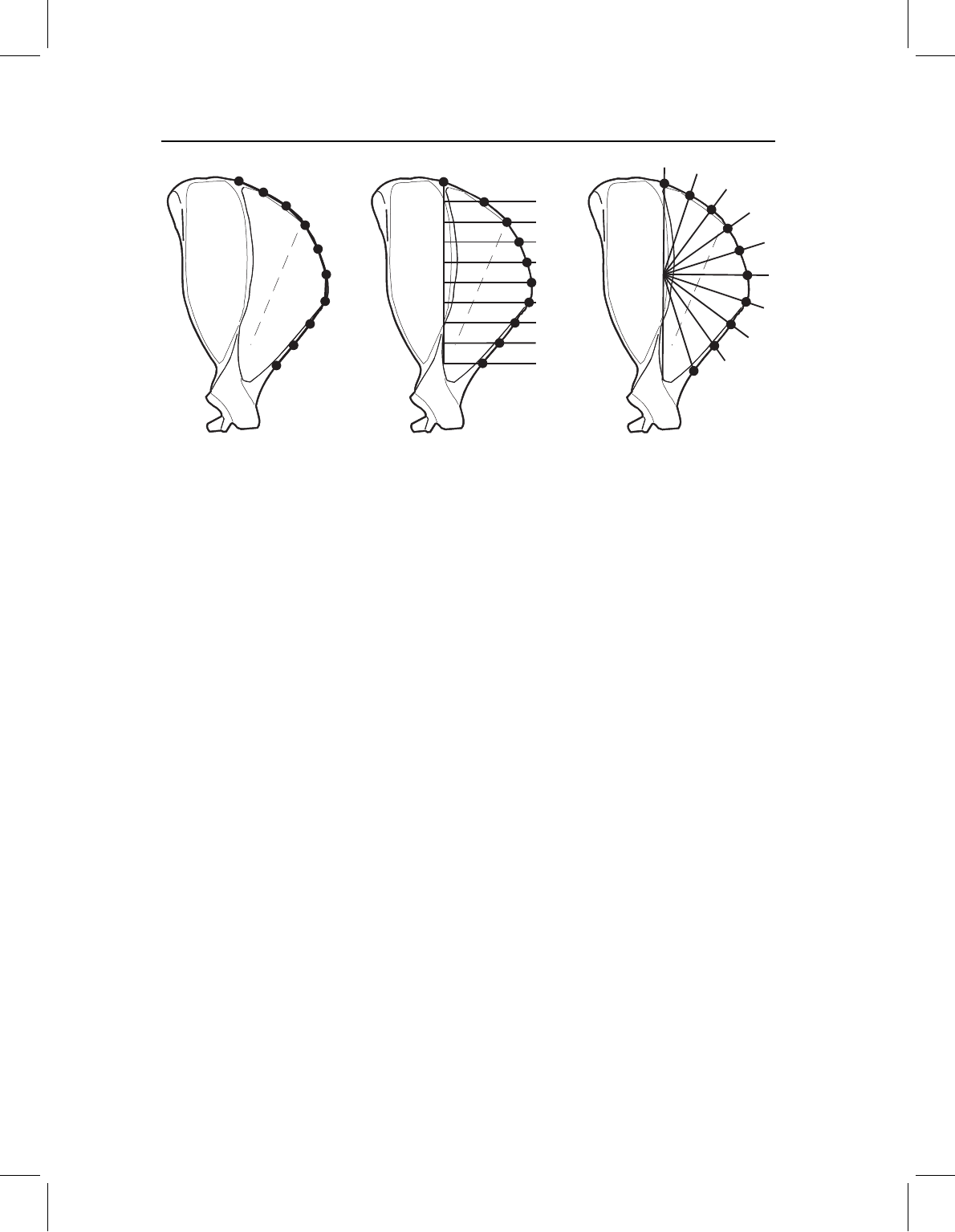
chap-15 4/6/2004 17: 29 page 397

BEYOND TWO-DIMENSIONAL CONFIGURATIONS OF LANDMARKS 397

(C)(B)(A)

Figure 15.6 Some general approaches to selecting semilandmarks on a curve, illustrated on the

anterior edge of a tree squirrel scapula: (A) increments of curve length; (B) increments of the chord;

differences. In this section we discuss possible adjustments to the process of computing GLS

Procrustes superimpositions of configurations of landmarks and semilandmarks (including

the option of making no adjustment); in the next section we discuss possible adjustments

to methods of ordination and statistical analysis. All of these issues are illustrated using

an artificial data set designed to represent a hypothetical pattern of shape variation in the

scapula of a tree squirrel (Figure 15.7).

No adjustment or weighting

In this simplistic approach, the semilandmarks are treated as equivalent to landmarks for

the purpose of computing superimpositions. (Treating the two as equivalent at this point is

independent of any differential weighting that might be applied subsequently in ordinations

or statistical tests, and does not preclude such weighting.) In this superimposition, the

semilandmarks of each specimen remain in the same positions relative to the landmarks

of that specimen. Figure 15.8A shows a GLS superimposition of the artificial scapula

data using this simplistic approach. The first principal component of variation (PC1) for

these data is primarily a change in the curvature of the anterior edge (Figure 15.8B): as

the anterodorsal corner becomes more squared, the ventral end becomes narrower. This

change in the anterior edge is correlated with a general change in the relative height of

the scapula and a rather small change in the anteroposterior lengths of the acromion and

metacromion (landmarks 2–5).

Because landmarks and semilandmarks are treated as equivalent, the configurations that

come out of the superimposition have the same shapes as the configurations that went into

the superimposition (which is not true of some alternative methods). In addition, the con-

figurations that come out represent shapes in Kendall’s shape space. At first glance these

appear to be clear advantages over any possible alternative method, but they could also be

considered disadvantages because they reflect a disregard for the fact that semilandmarks

are not equivalent to landmarks. Because landmarks and semilandmarks are treated as