Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

chap-13 4/6/2004 17: 28 page 328

328 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Table 13.2 Allometric coefficients, k, computed by multi-

variate regression (R) and PCA (variable 1 is the independent

variable in the multivariate regression; its value of k must be

included to make these vectors comparable)

Variable R PCA

v1 1.000 0.694

v2 0.806 0.559

v3 0.885 0.614

v4 0.850 0.589

v5 1.225 0.851

v6 1.042 0.723

v7 1.002 0.696

v8 0.928 0.644

v9 1.104 0.766

v10 1.220 0.847

v11 1.198 0.832

v12 1.136 0.789

v13 1.186 0.823

v14 1.116 0.775

v15 1.210 0.840

v16 1.225 0.850

v17 1.171 0.813

v18 1.170 0.812

v19 1.085 0.753

v20 1.104 0.766

v21 1.225 0.850

v22 1.217 0.845

v23 1.072 0.744

v24 0.939 0.651

v25 1.120 0.777

v26 1.129 0.783

v27 0.898 0.623

v28 0.811 0.563

v29 0.751 0.522

v30 0.903 0.627

regressed on SL. We should note that the literature is inconsistent on the symbols used for

these two coefficients.

Usually, the coefficients are estimated by simple bivariate regression (both ordinary

least squares, OLS, and reduced major axis, RMA, regression). As shown in Chapter 10,

multivariate least squares regression yields the same estimates as obtained from bivariate

analysis so we can treat the bivariate estimates of k as components of the vector {k

, k

,…k

} (where P is the number of measurements) and those of log(b) as components of

the vector {log(b

), log(b

), … log(b

)}. Another common multivariate approach

is principal components analysis (PCA); Jolicoeur (1963) first proposed that PC1 is a

multivariate allometry vector when PC1 is extracted from a variance–covariance matrix

of log-transformed measurements. Conceptually, multivariate regression and PCA differ

in that PCA does not single out one variable as independent. Instead of treating one of

chap-13 4/6/2004 17: 28 page 329

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 329

Table 13.3 Ratios between allometric coefficients, k, of each

variable and standard length (v1), for the coefficients computed

by multivariate regression (R) and PCA

Variable R PCA

v2 0.81 0.81

v3 0.89 0.88

v4 0.85 0.85

v5 1.23 1.23

v6 1.04 1.04

v7 1.00 1.00

v8 0.93 0.93

v9 1.10 1.10

v10 1.22 1.22

v11 1.20 1.20

v12 1.14 1.14

v13 1.19 1.19

v14 1.12 1.12

v15 1.21 1.21

v16 1.23 1.22

v17 1.17 1.17

v18 1.17 1.17

v19 1.09 1.09

v20 1.10 1.10

v21 1.23 1.22

v22 1.22 1.22

v23 1.07 1.07

v24 0.94 0.94

v25 1.12 1.12

v26 1.13 1.13

v27 0.90 0.90

v28 0.81 0.81

v29 0.75 0.75

v30 0.90 0.90

the observed variables as the measure of size, PCA constructs a multivariate size measure

from the observed variables; scores on PC1 are the measures of size. Also, OLS multivariate

regression presumes that the independent variable is measured without error, whereas PCA

does not.

Regression (both OLS and RMA) and PCA tend to give very similar results when mea-

surements are highly correlated, which they usually are in studies of ontogenetic series. For

example, Table 13.2 shows the estimates of the slope for the measurements of S. gouldingi

obtained by Model I regression (OLS) and PCA. The numbers may appear to be quite

different, but these differences disappear when the coefficients are rescaled so that each is

the ratio between the k for one variable and the k for SL. Because SL is the independent

variable, k

=1.

Rescaling the coefficients of PC1 by dividing each coefficient by that for SL gives the

values shown in Table 13.3. The estimates obtained by multivariate regression and PCA

chap-13 4/6/2004 17: 28 page 330

330 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

are identical. Perhaps the most important distinction between regression and PCA is that

PCA does not provide estimates of b.

Interpreting allometric coefficients

The interpretation of k is straightforward – it is the growth rate of one measurement

relative to that of a standard, the growth rate of X. When k is 1.0, the growth of the part

keeps pace with that of X, which we will take as the whole body – i.e. their proportions

are constant throughout growth. Such measurements are termed “isometric.” When k

is greater than 1.0, the part increases its size relative to overall body size; these parts

are termed “positively allometric.” When k is less than 1.0, the part decreases in its size

relative to body size; these measurements are termed “negatively allometric.” Only one

measurement in Table 13.1 is isometric, but many coefficients are equal to each other, so

we could view them as isometric relative to each other. We are not constrained to think of

solely in terms of growth rates of each part relative to body size – all ratios among the k

are relative growth rates as well. Several measurements are isometric relative to each other,

including the four measurements of body depth (measured from landmarks 4 and 5, which

are at the anterior and posterior bases of the dorsal fin). These four (v15, v16, v21 and

v22) grow at equal rates relative to each other, so relative to each other their proportions

do not change over ontogeny. All four are positively allometric relative to body length, so

the body (in that region) deepens relative to its length. Among the negatively allometric

measurements are the most anterior lengths (v2, v3, v4, v8, v28, v29, v30) and the two

most posterior ones (v24, v27). This means that measurements in the anterior head and

caudal regions shorten relative to the whole body (of course they do not actually shorten –

they lengthen in an absolute sense, it is just that they shorten relative to the length of the

body). Consequently, the head and caudal region form a relatively smaller fraction of body

length in adults than in juveniles.

The interpretation of b is less straightforward, and there has been some controversy

about its biological meaning. One reason for doubting that b has any general biological

significance is that its value depends on the units of measurement; unlike k, b is not a

dimensionless quantity. However, a more important one is that log(b) is the value of

log(Y) when log(X) is zero, a size at which Y might not yet exist. For example, when

the body is 1 mm long, the dorsal fin might not have developed yet so it cannot have a

meaningful size. Additionally, log(b) is estimated under the assumption that k is constant

from log(X) =0, not just that it is constant over the range of values actually sampled.

Under one condition, b does have a simple interpretation. When populations do not

differ in k, a difference in b does have a meaning because the difference in b will persist

throughout the entire ontogeny. Even if we hesitate to infer a value for log(Y) when

log(X) =0, under the condition that both species have the same value of k, the regression

lines would differ only in elevation. So at any point in ontogeny, they will differ in elevation

according to their difference in b. We might reasonably hesitate to claim that they have

diverged by the time that log(X) =0, but we could claim that the difference between the

species arose prior to the stage when we first observe them, and it is invariant throughout

the rest of ontogeny. That difference in b says how those populations will differ at any

given value of X. For example, if we are comparing the brains of several species that do

not differ in k, we can determine their relative brain size at all body sizes by comparing

chap-13 4/6/2004 17: 28 page 331

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 331

1.17

1.10

1.12

1.09

.94

.90

1.12

1.07

.93

.81

1.14

1.22

1.23

1.17

.75

1.20

.90

1.04

1.22

1.21

1.23

1.13

1.10

.89

1.00

.81

.85

1.23

1.19

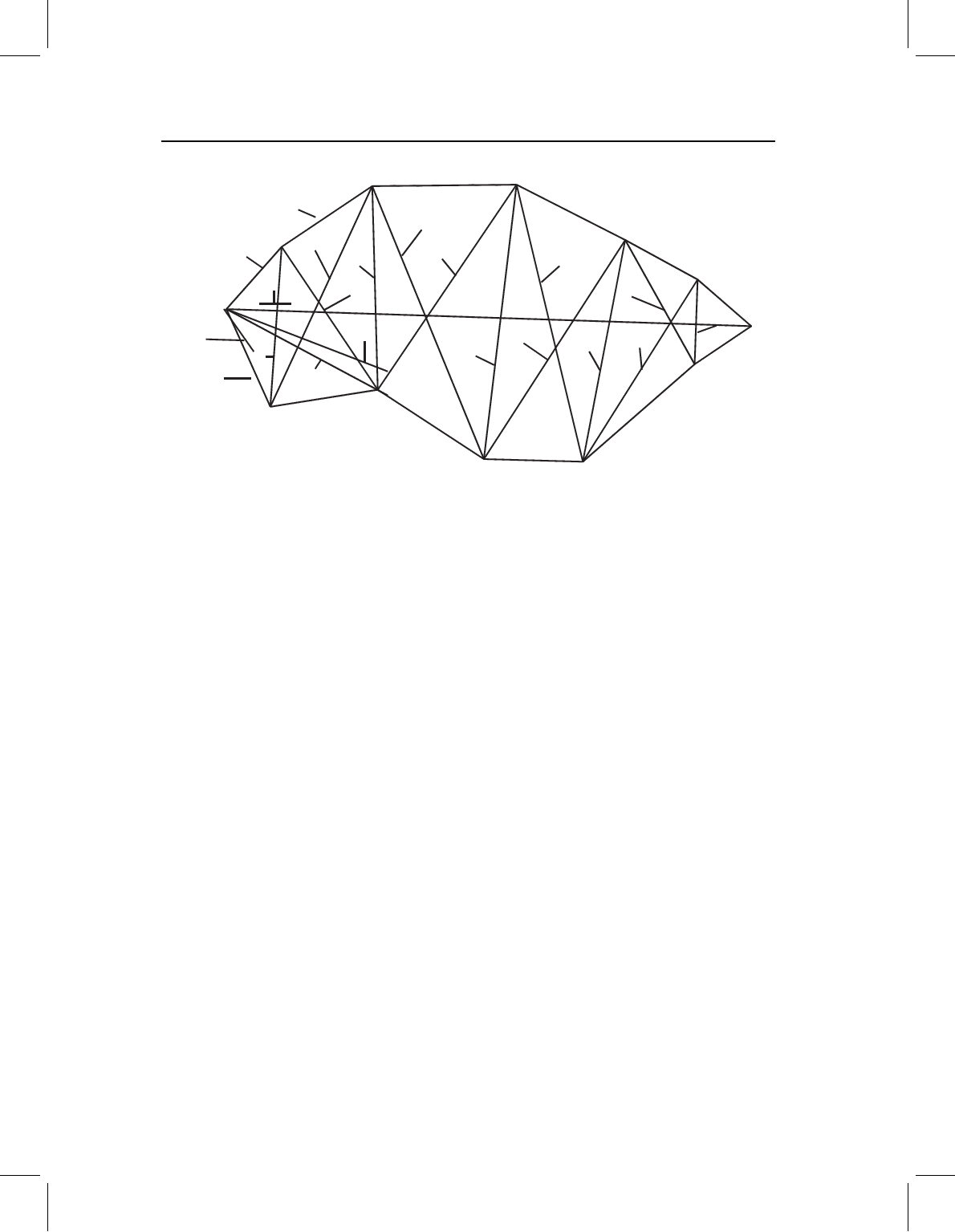
Figure 13.4 Allometric coefficients of Serrasalmus gouldingi. Coefficients significantly higher than

1.0 indicate positive allometry, coefficients significantly lower than 1.0 indicate negative allometry,

and those between that cannot be distinguished statistically from 1.0 indicate isometry.

b; in this specific context, b has been termed an “index of cephalization” (see White and

Gould, 1965). When k does not differ, b can be viewed as a scaling parameter. Under

other conditions, b is just a parameter needed to predict Y at a given value of X.

The developmental meaning of b and k

Having defined b and k mathematically, and discussed how to estimate and interpret them,

we can now consider their developmental meaning. Most of the theoretical literature has

focused on k because b is static – it is not a descriptor of development, just of where the

regression line intersects the Y-axis. At the heart of the literature is the view of growth as

a multiplicative process. This was the rationale given by Huxley (1932) for the power law,

and it is the basis for cellular models of allometric growth (e.g. Katz, 1980). Within that

context, the meaning of k has been viewed from both spatial and temporal perspectives.

Huxley (1932) emphasized the spatial interpretation of k, proposing that changes in k

over the organism indicate spatially organized “growth intensities.” He noted that values

of k tend to be spatially coherent, rising and falling in organized patterns across the body.

To help visualize spatial patterns in k, we can first put the coefficients on the organism

rather than in a table (Figure 13.4). We can see that they increase from the head to the

middle of the body, then fall towards the tail, although not to a level as low as found

in the head. This is (approximately) an inverted U-shaped gradient, which is interesting

because it is the inverse of the gradient found in several teleost larvae (Fuiman, 1983).

This suggests that the allometry of juvenile growth, in effect, compensates for that of

larval growth: the head and caudal body initially grow very rapidly, and the middle of the

body catches up during juvenile growth. Growth rates can also suggest anteroposterior

gradients, which means that they fall off linearly from the head to the tail. To analyze

chap-13 4/6/2004 17: 28 page 332

332 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

0.8

0.9

1.0

1.1

1.2

1.3

Position along anteroposterior axis

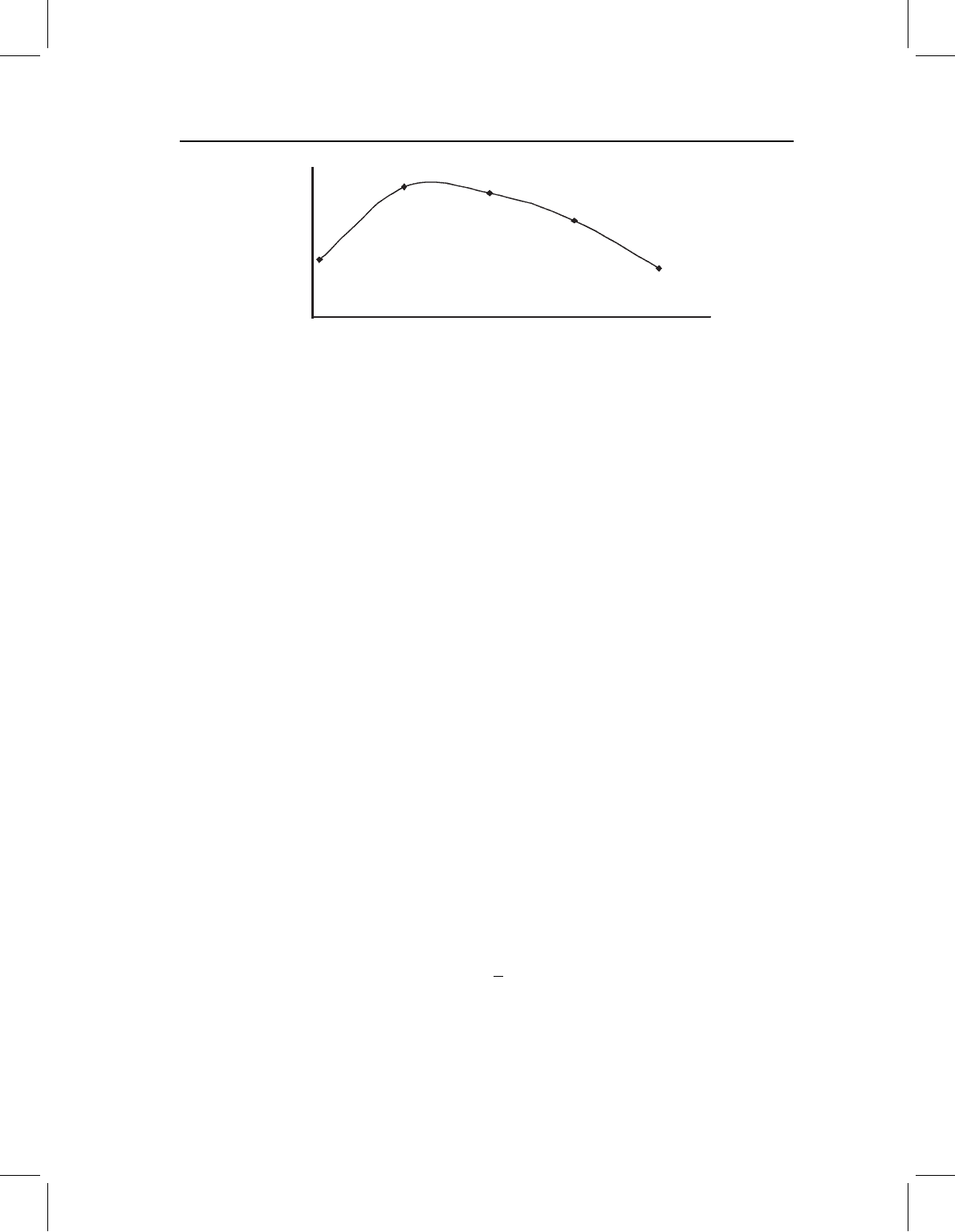
Figure 13.5 Growth profile for relative growth rates along the anteroposterior axis of S. gouldingi.

Allometric coefficients for measurements of growth along the anteroposterior axis are plotted as a

function of the ordinal position of the measurement (anterior is to the left of the plot, posterior to

the right).

these patterns more rigorously Huxley constructed “growth profiles,” which are plots of

allometric coefficients as a function of their position along body axes. Unfortunately, few

studies record the position of a measurement along a body axis (they were not recorded for

the measurements shown in Figure 13.3, for example). As a crude approximation we can

order the measurements in a linear sequence, ordered from anterior to posterior, and plot

allometric coefficients at each ordinal position (Figure 13.5). Although it would clearly be

better to have more accurate estimates of position along the body, the plot is nonetheless

intriguing because it suggests a spatial ordering to the coefficients. Remarkably few recent

studies have used growth profiles to understand developmental spatial patterning or its

evolution (one exception is the analysis by Fuiman mentioned above, another is Zelditch

et al., 2001).

Laird and colleagues have stressed the temporal significance of allometric coefficients

(e.g. Laird 1965; Laird et al., 1968). Even though time is not explicitly incorporated in

studies of allometry, it is nonetheless implicit. This becomes evident when considering

why the power law holds in the first place. As mentioned before, the primary biological

explanation for allometry is that growth is a multiplicative process. When analyzing the

relationship between size and time, the best-fitting models are usually not linear but rather

are sigmoidal in form. An important feature of these models is that growth rates decay

over time. Similarities in decay rates are interpreted by Laird (1965) as the explanation for

the linear relationship among log-transformed measurements. In effect, all measurements

follow the same growth curve; their differing values of k tell us how they are displaced

relative to each other in time – different parts of the body reach the same point on their

growth curves at different times. Laird et al. (1968) elaborated on this theory, stating the

relationship between k and lag time (T) as:

T =−

ln(k)(13.3)

where α is the decay rate and k is an allometric coefficient.

We cannot measure decay rates without information on age, but we can use Equa-

tion 13.3 to understand the temporal relationships among growth curves so long as we are

willing to assume that decay rates are the same for all measurements whose logs are linearly

chap-13 4/6/2004 17: 28 page 333

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 333

related. Because growth rates decay over time, we would intuit that a more negatively allo-

metric part has decayed over a longer time, and that it has decayed for longer because it

began growing earlier. The increment of time by which we need to shift one curve to match

another that starts growing later is T. Based on this interpretation of allometric coeffi-

cients, we would conclude that the head and caudal peduncle develop before the midbody,

that the eye is the first structure to develop, and that the body elongates before it deepens.

The spatial and temporal perspectives on allometric coefficients are not antagonistic.

The spatial coherence noted by Huxley, interpreted within the temporal framework of

Laird, suggests that growth is spatiotemporally organized. There is no reason to think

that either space or time is primary. We do not need to adopt one view over the other –

they are mutually consistent, and help explain each other. With increasing information

about the spatial determination of development, in conjunction with that on its tempo-

ral organization, we can relate allometric coefficients to the underlying developmental

processes that explain them. Because these theories of developmental controls over the

spatiotemporal organization of relative growth may be most easily expressed in terms

of traditional morphometric measurements, studies of allometry using traditional mor-

phometric measurements will remain an important part of evolutionary developmental

biology.

Of course, allometric coefficients are also informative about the relationship between

form and function. The literature on biomechanics is filled with theories that predict scal-

ing relationships among measurements. Applied to ontogenetic series, such theories may

explain ontogenetic allometry in terms of the ontogeny of function. For example, in many

larval teleosts the head and caudal region are highly positively allometric, which is due

to the early demands imposed by swimming, feeding and respiratory systems (see, for

example, van Snik et al., 1997). The converse allometric pattern is seen later, in juvenile

growth, as exemplified by the coefficients of S. gouldingi. These patterns are hardly surpris-

ing, which is reassuring if our aim is to make sense of ontogenetic allometry in functional

and ecological terms.

Comparative analysis of ontogenetic allometry: traditional

morphometric data

Comparative studies of ontogenetic allometries serve two primary purposes. First, they

test general theories about the relationship between form, function and development. For

example, considerations of function suggest that, generally, teleosts ought to share the pos-

itive allometry of the head and caudal body during larval growth, with postlarval growth

being characterized by positive allometry of the region between. Comparative studies can

test that general hypothesis, and pursue more refined theories of the ontogeny of func-

tion should the expected pattern be less general than anticipated. Second, comparative

studies test theories about the evolution of development and the impact of evolving devel-

opmental systems on morphological diversity (= disparity; see Chapter 12). For example,

we might anticipate that early development is more conservative than later development

because modifications of early development are likely to have dramatic consequences for

later phases. Of course, we would not anticipate that this would be the case for organisms

that have distinct metamorphic phases, because metamorphosis can decouple phases of

chap-13 4/6/2004 17: 28 page 334

334 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

development. Consequently, each could evolve independently. Therefore we could state

the theory as comprising two parts: (1) in organisms that have continuous development,

early stages are more conservative than later ones; and (2) early development is more

conservative in organisms that have continuous development than in those with distinct

metamorphoses. Testing such general theories about the evolution of growth and morpho-

genesis, including theories about heterochrony, is another major rationale for comparative

allometric studies.

Below we have classified a variety of evolutionary patterns according to the changes in

development producing them and the resultant relationship between ontogeny and phy-

logeny. We first discuss parallelism or channeling (for the remainder of this chapter we will

use the term “channeling” rather than parallelism, because we are talking about coinci-

dent rather than parallel lines). This pattern is characterized by species that have the same

shape at the outset of differential growth, as well as a common direction of allometry.

Biologically, channeling results from changes in the rates or timings of development along

a conservative ancestral ontogeny. The second class includes modifications of the onto-

genetic trajectory itself – not just its relationship to growth or age. These involve changes

in the spatiotemporal organization of development, and we can subdivide them according

to the phases affected: (1) changes confined to early morphogenesis (which we typically

infer only by their affects on proportions at the outset of allometric growth); (2) changes

in the spatiotemporal organization of growth from the outset to end of allometric growth;

and (3) changes in spatiotemporal organization of growth confined to late development.

There is an additional, heterogeneous category: complex changes in multiple processes

and stages.

Below, we describe several patterns in more detail, focusing first on the relationship

between ontogeny and phylogeny engendered by each and their consequences for disparity,

and finally on the criteria whereby they can be distinguished empirically.

Channeling

Channeling refers to the case in which the descendant adult morphology lies along the

ancestral ontogeny because the ancestral and descendant ontogenies begin at the same

starting point and proceed in the same direction. Representing this pattern in terms of

a plot of log(Y)onlog(X), channeling occurs when the descendant merely extends or

truncates the ancestral ontogeny; graphically, scaling can be seen in plots of log(Y)on

log(X) – both ontogenetic series start at the same point and lie on the same line, it is just

that one species extends that line further (Figure 13.6A). Consequently, the direction of

evolutionary change lies along the vector describing the ancestral ontogeny (Figure 13.6B).

This is the pattern that Gould calls “parallelism” (Gould, 1977), and it is expected when

the species differ solely in rate or timing of either growth or development. It implies that

rate or timing evolve, but the ancestral pattern of relative growth rates (both larval and

postlarval) is conserved.

We subdivide channeling into two types because growth and development can either

be associated or decoupled. If they are associated, the descendant has the shape expected

for its size – e.g. it looks young for its age because it is small for its age. Organisms that

look young for their age are called paedomorphic (from “child-like”). Descendants might

also look old for their age because they are large (they are called peramorphic because

chap-13 4/6/2004 17: 28 page 335

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 335

log(X )

log(Y )log(Y )

(A)

(B)

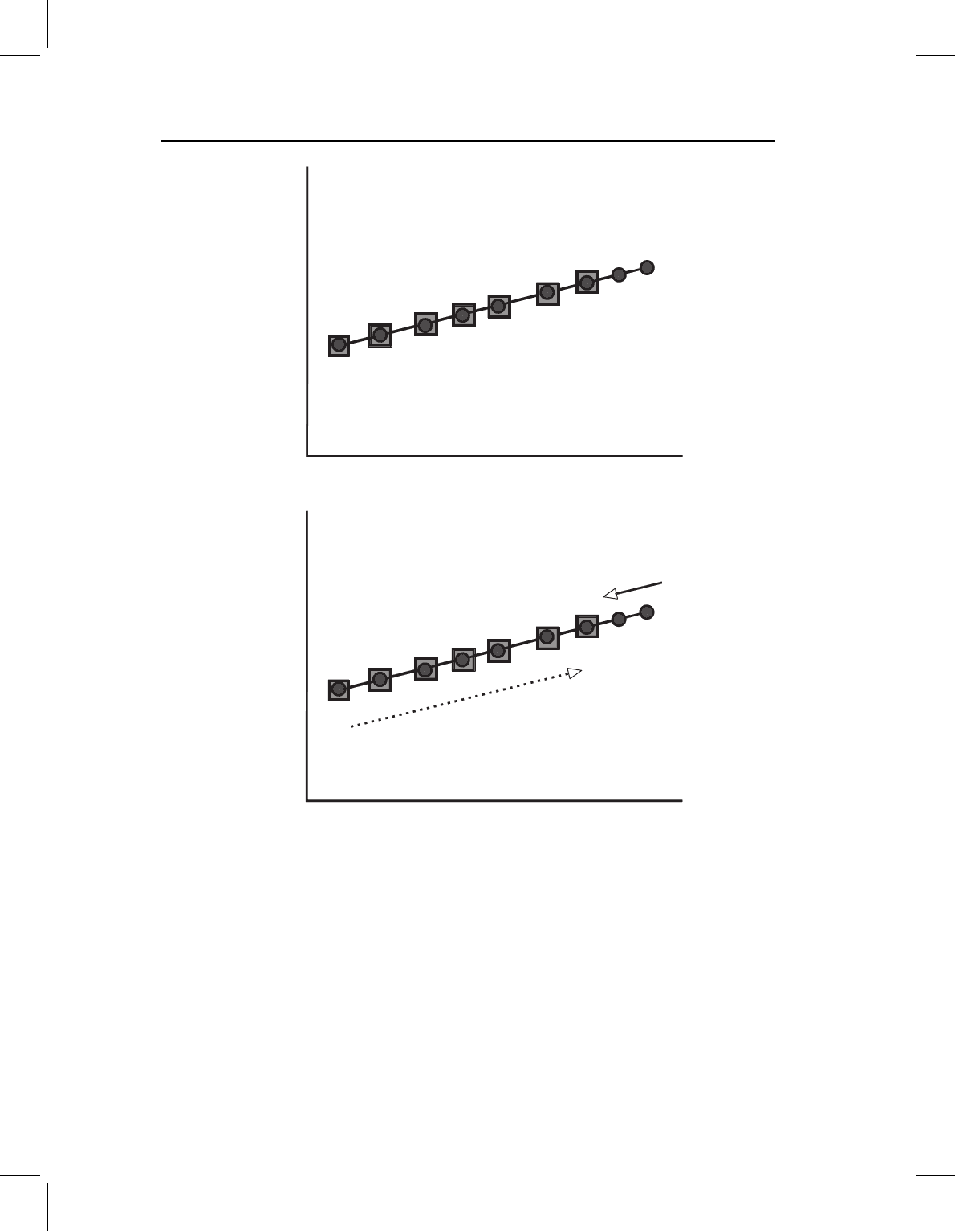
Figure 13.6 Channeling by ontogenetic scaling, depicted by a bivariate plot of log(Y)onlog(X).

The same pattern will be found for all the measured Y variables, thus the pattern can be represented

by a single bivariate plot. (A) Ontogenetic allometries of ancestor (circles) and descendant (squares);

(B) the directions of ontogenetic (O) and evolutionary change (E).

they go through and beyond the endpoint of the ancestral ontogeny). In the latter case,

the descendant adult morphology does not actually appear in the ancestral ontogeny, but

it results from extending it. However, it is possible to be paedomorphic and large, and

also to be peramorphic and small. These are cases in which growth and development are

decoupled – for example, developmental rates might be reduced without a corresponding

reduction in growth rates, so the descendant reaches maturity before it attains the ancestor’s

adult morphology even though it reaches the ancestor’s adult body size. The empirical

chap-13 4/6/2004 17: 28 page 336

336 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

criteria for documenting ontogenetic scaling differ in an important respect from those that

document channeling via decoupling of growth from development. For that reason, we

discuss the empirical criteria separately.

Empirical criteria for documenting ontogenetic scaling

Of all the various modifications of development, ontogenetic scaling is the easiest to detect,

at least in principle. The biological hypothesis predicts that species differ only in adult body

size, not in either {b

, b

,…b

}or{k

, k

,…k

}. For the remainder of this chap-

ter, we will refer to {b

, b

,…b

} rather than {log(b

), log(b

), … log(b

)} to

simplify the presentation. Given this hypothesis, we can use MANCOVA to test it. How-

ever, given our expectations of no evolutionary change in either vector, using MANCOVA

poses a problem – the substantive biological hypothesis is equivalent to the statistical null.

Normally we think of the null as the hypothesis we would like to reject, and we use various

strategies to ensure that we do not reject it too readily. However, the hypothesis of scaling

is the one we wish to accept, so we are put in an odd position. One consequence is that

all the factors that normally can prevent us from rejecting a false null hypothesis, such as

lack of statistical power/small sample size, favor accepting a false hypothesis of scaling.

A second problem that arises in many studies is that many of the variables imply scaling,

but a few others do not. Viewed from a bivariate perspective, this means that many traits

undergo scaling but a few do not. However, viewed from a multivariate perspective, it

means that the organism is not a scaled up or down version of its ancestor because not all

traits are scaled up or down. It also means that either early or late development is altered,

depending on whether the departures from scaling involve {b

, b

,…b

}or{k

, k

,…k

} (and they could both be involved). Whether those modifications are trivial or

consequential depends on how far they deviate from scaling, and what their consequences

are for morphology. We therefore need measures of the deviations from the expectations

under the hypothesis, as well as measures of the impact of those deviations on {y

, y

, ...y

Because the hypothesis predicts that both species will have the same vector {k

, k

,…k

}, we would predict that the interspecific angle between those vectors will be 0.0

◦

;

we can test that hypothesis using the methods introduced in Chapter 10. However, we

also need to have a feel for the magnitude of the angle. In analyses based on traditional

morphometric data, angles will rarely be large, even if the vectors are no more similar

than expected by chance. Being no more similar than expected by chance does not mean

that the angle will be 90

◦

. To understand why that is the case, it is necessary to recall

how those angles are calculated, as well as to appreciate the meaning of k. The angles are

computed by taking the dot product between the two vectors, which means we multiply

of one species by k

of the other, and add that to the product of k

in one species by

of the other, and so forth; so we are summing products of corresponding allometric

coefficients. These coefficients are the power to which body size is raised in the power

law (Equation 13.1). So long as structures grow over ontogeny, k is invariably a positive

number. The coefficients rarely differ by much – the most extreme values for S. gouldingi

are 0.75 (for eye diameter) and 1.23 (for midbody depth and posterodorsal head length).

That difference may seem very large because one is highly negatively allometric whereas

chap-13 4/6/2004 17: 28 page 337

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 337

the other is highly positively allometric, but the difference is still numerically very small

(in this case, it is less than 0.5).

Because all the elements of both vectors are positive numbers, the sum of their products

cannot be zero – much less negative. To produce an angle of 90

◦

, the sum would have to be

zero (because the cosine of 90

◦

is zero). The angle is necessarily smaller than that – often

very much smaller. To appreciate how small it can be when vectors are independent, we

can compare a vector of ontogenetic allometric coefficients to 400 random permutations

of it. In the case of S. gouldingi the average vector correlation over those 400 random

permutations is 0.9812 with a confidence interval of 0.9754–0.9874, corresponding to an

angle of 11.13

◦

with a confidence interval of 9.10

◦

–12.74

◦

. Therefore, only correlations

higher than 0.9874 (or, equivalently, angles smaller than 9.10

◦

) indicate any greater sim-

ilarity than expected by chance. It may seem unreasonably strict to insist that the angle

cannot be much greater than 0

◦

, but in light of the large differences implied by very small

angles, we cannot document scaling if angles much exceed 0

◦

If the vectors of allometric coefficients are different, we cannot compare the vectors

of b by MANCOVA. However, we do not actually need to compare them because we

have already rejected the hypothesis of scaling by finding a significant difference in {k

, k

,…k

Empirical criteria for documenting a decoupling of growth from development

When growth and development are decoupled, we anticipate changes in {k

, k

,…k

but only those consistent with the hypothesis that development is conserved. The specific

expectations may seem strikingly counterintuitive; rather than simply stating them, we

will derive them from the meanings of paedomorphosis and peramorphosis. Paedomor-

phosis means that the descendant adult resembles the ancestral juvenile morphology – over

ontogeny it does not depart as far from the shared juvenile morphology. The extreme case

is an adult that does not depart at all from the juvenile morphology, meaning its growth

is isometric (it does not change shape as it grows). In less extreme cases, we expect the

descendant ontogeny to be more nearly isometric than the ancestor’s. Based on that rea-

soning, we can predict that positively allometric coefficients will decrease in slope whereas

negatively allometric coefficients will increase because positively and negatively allometric

coefficients approach isometry from opposing directions. An example of a pattern expected

under this hypothesis is shown in Figure 13.7.

Of course, the coefficients must all change by the appropriate amount. Considering

that paedomorphosis results from truncating the ancestral ontogeny, and peramorphosis

from extending it, we would anticipate only a change in the length of the ontogenetic

trajectory – the two vectors of allometric coefficients should otherwise be the same. Thus,

we anticipate an angle of 0.0

◦

between vectors. Framing the hypothesis of a conserved

larval morphology is more complicated because we cannot test the coefficients {b

, b

,…b

} owing to the differences in {k

, k

,…k

}. Above, we determined that we do

not need to test the hypothesis that {b

, b

,…b

} does not differ because the differences

in {k

, k

,…k

} rule out the hypothesis of scaling. However, we are no longer asking

whether size predicts shape. It is possible that species do not differ in proportions at

the smallest observed stage (even if they differ in proportions at any given size). Thus,

instead of comparing {b

, b

,…b

} we compare the expected shapes at a comparable

Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.