Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-12 4/6/2004 17: 27 page 298

298 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

where D

is the distance of species j from the overall centroid (which is the grand mean

calculated over the n species or other groups being analyzed). We can use Equation 12.1

to calculate both size and shape disparity. For size data, D

is the difference between the

centroid size of an individual species and the grand mean centroid size. For shape data,

is the Procrustes distance between the average shape of an individual species and the

grand mean shape. We can compute shape disparity directly by estimating those Procrustes

distances, or we can calculate the variances of coordinates obtained by a generalized least

squares Procrustes superimposition (GLS) or variances of partial warp scores (including

scores on the uniform component). All three approaches yield the same results because the

sum of squared coordinates obtained by GLS equals the squared Procrustes distance to the

mean, as does the sum of squared partial warp scores. In those analyses the grand mean

shape is the consensus, so if we are using partial warps we can use the formula:

MD =



j=1

(N − 1)

(12.2)

where PW represents the partial warp scores for an individual, so the formula tells us to

sum all the squared partial warp scores for each individual over all individuals. Because

the grand mean shape is the consensus, its partial warp scores are all zeros, so Equation

12.2 is equivalent to Equation 12.1.

Both are also equivalent to:

MD = Tr{S} (12.3)

where Tr is the trace of a matrix (the sum of its diagonal elements) and S is the variance–

covariance matrix of the partial warp scores (including the uniform component, and

computed using the grand mean as the consensus). The diagonal elements of a variance–

covariance matrix are the variances, so this formula tells us to sum the variances of the

variables, which takes us back to the squared distances from the consensus.

To exemplify the analysis of disparity, we will measure the disparity of adult body shape

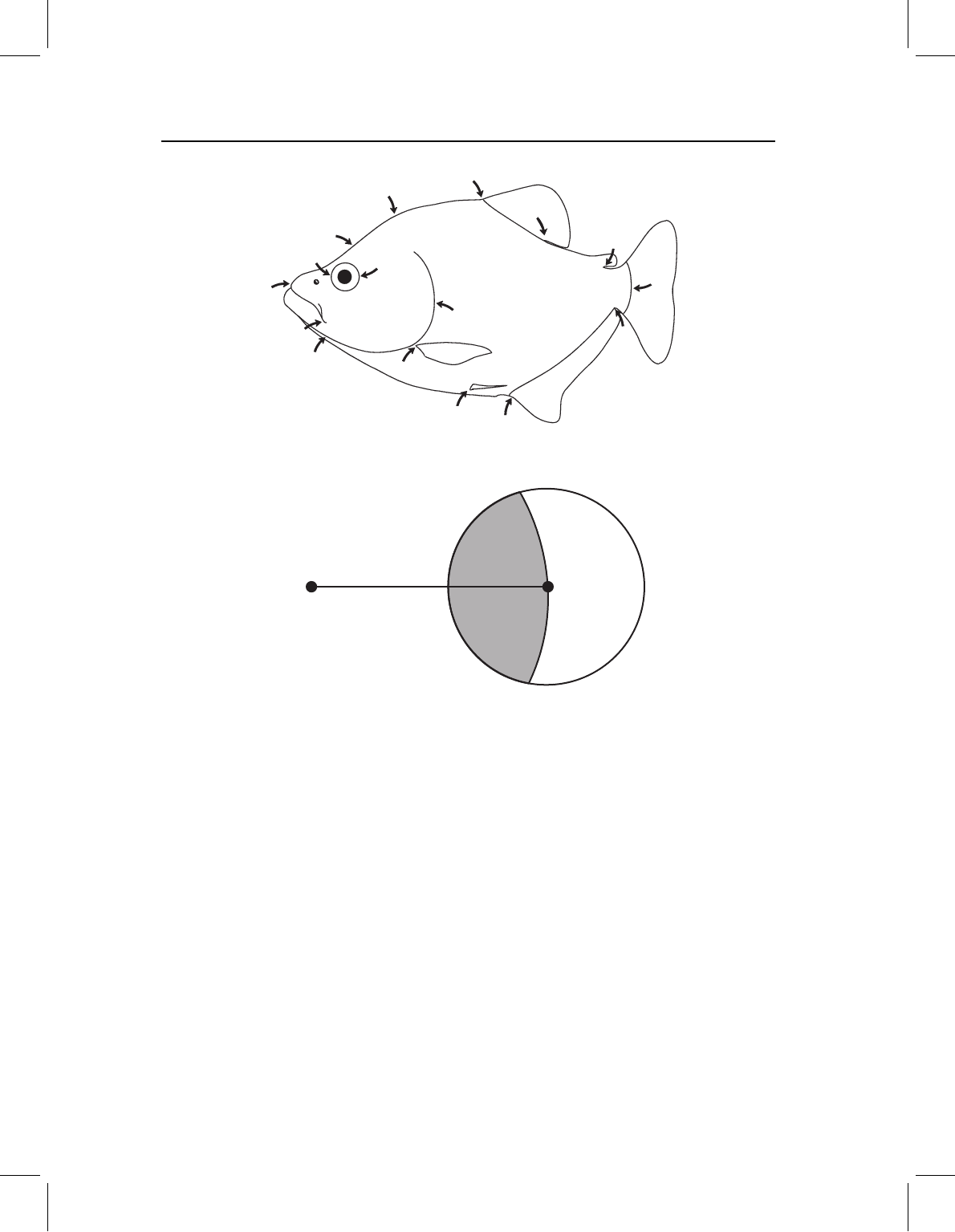
of nine species of piranhas sampled at the 16 landmarks shown in Figure 12.1. Before doing

this analysis, we remove the shape variance within each species that is due to ontogeny,

allowing us to estimate the shape of an average adult (this is done by standardizing each

species to its maximum adult size, as explained in Chapter 10). Each species is represented

by a single data point, the mean shape for that species. There are nine species, so N =9.

The result of the analysis is that MD =0.00398. Of course, we cannot yet interpret this

number – we cannot say if that value is large or small, or how uncertain it is. Before we

can go any farther, we need to deal with the issue of uncertainty.

Placing confidence intervals on morphological disparity (MD)

To construct the confidence interval, we need first to consider the various parameters

being estimated. In general, there is uncertainty in the estimate of the mean shape of each

species, and in the estimate of the consensus. Both uncertainties must be taken into account

when putting confidence intervals around MD. Additionally, when the mean shape of each

species is calculated by removing the variance due to ontogeny (or some other factor) we

must also account for the uncertainty of the regression model used to standardize the

chap-12 4/6/2004 17: 27 page 299

DISPARITY AND VARIATION 299

Figure 12.1 Landmarks sampled on the external body form of piranhas.

Grand

mean

Species’

mean

Figure 12.2 The line joining a species’ mean to the grand mean; random variation in the position of

the mean only rarely lies along the line within the shaded region. Changes in the position of shapes

orthogonal to that line or within the unshaded region increase the distance to the mean.

shapes. We may also need to take a further source of uncertainty into account – the samp-

ling of species, because unless we have measured them all we must consider the uncertainty

of the grand mean that arises from our sampling of species. If we do not consider this par-

ticular source of uncertainty, we cannot generalize from our sample of species to the larger

group that includes them, although we can make statements about our particular sample

of species that takes the uncertainty of our sampling of them into account.

The confidence intervals might look odd because they frequently are not symmetric

about the mean, even when the distribution of shapes around the GLS consensus is sym-

metric. That symmetric distribution of shapes implies that the uncertainty in the estimate

of the mean is roughly equal in all directions (i.e. it is a hyperspherical solid). Turning

to the estimates of disparity, we can see why the uncertainty in the distance of a species

from grand mean is not symmetric about the mean distance even then. The hyperspherical

distribution of uncertainty in the mean yields a non-symmetric distribution of distances –

there are many more possible locations of a species’ mean that increase the distance than

there are that decrease it. As we can see in Figure 12.2, the line joining the grand mean to a

chap-12 4/6/2004 17: 27 page 300

300 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

species’ mean is in a single direction in a high dimensional space; random variation in the

position of the sample mean rarely lies along the line between the species’ mean and grand

mean. In Figure 12.2, D is the distance from the species’ mean to the grand mean shape,

and the circle around X represents the range of uncertainty about the species’ mean. The

region within the circle that is a distance D or less from the grand mean is shaded, and this

region is clearly smaller than the unshaded region that is farther than D from the grand

mean. This effect is even more pronounced in higher dimensions.

We can construct confidence intervals and standard errors for MD by bootstrapping.

When we need to take the uncertainty of the regression into account, we first fit a regression

model to the data, then use the procedure described in Chapter 10 – determining the

residuals, predicting the shape expected for each size, bootstrapping the residuals and

randomly allocating them to each predicted shape, then refitting the regression model to

the data to generate a standardized data set for the bootstrap set. This is iterated N times

(where N is the number of bootstrap sets). If we do not need to take the uncertainty

of the regression into account, we simply resample (with replacement) from each of the

samples. For each bootstrap set of standardized values, we calculate the disparity of that

sample using the formula for MD above. In the case of the adult piranhas discussed above,

the estimate of MD =0.00398; the 95th percentile over the bootstrap sets gives us the

two-tailed confidence interval on that estimate, 0.00377 to 0.00440.

We still do not know if that value is large or small because we have still not compared it

to the disparity of anything else. We will thus continue the analysis, comparing the levels

of adult disparity to that of juveniles, and comparing the disparities of several piranha

clades (Figure 12.3).

Example: ontogenetic and interclade comparisons of disparity

Table 12.1 gives the disparities (MD) of juvenile and adult shapes, as well as the standard

errors (SE) for the estimates. As explained in Chapter 9, we can use a t-test to determine

whether derived traits like mean disparities are significantly different:

t =

−MD









−1)N

+(N

−1)N

−2







(12.4)

with (N

−2) degrees of freedom. Because MD is computed from the mean shapes

of species, N

and N

are the numbers of species in the respective clades. We can also use

a bootstrap procedure like that used to test whether two Procrustes distances are different.

We begin by computing the disparities of the two groups and the difference between those

disparities, then we resample each data set with replacement and repeat the calculation of

the disparities and the difference between them. After a sufficient number of bootstraps,

we can determine the 95% interval for the range of differences. If this range excludes zero,

we can conclude that the observed difference is significant at the 95% level.

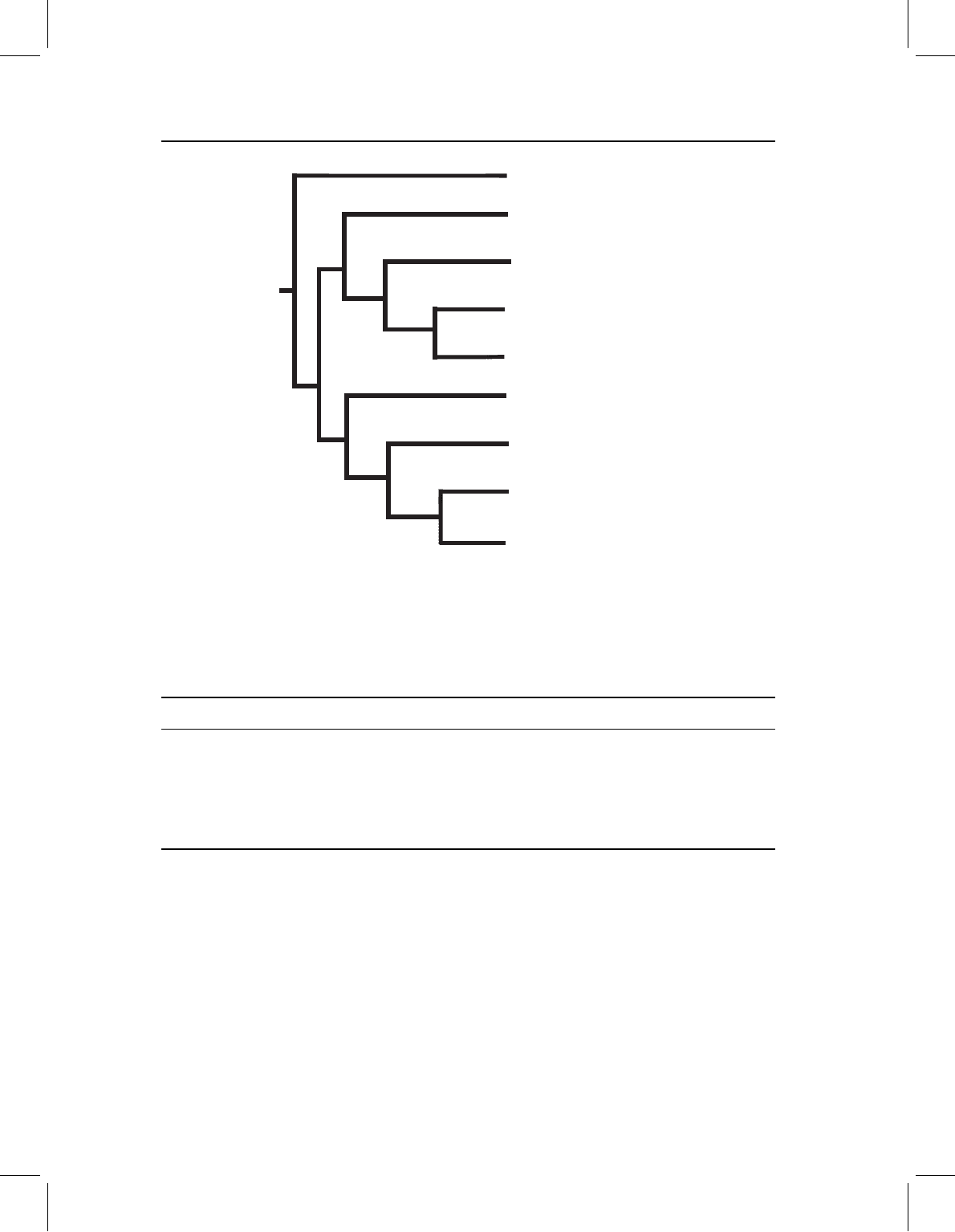
For the most inclusive piranha group (Clade 1), disparity decreases significantly over

ontogeny, as it does in Clade 2. In Clade 3, disparity increases statistically significantly,

but the change is slight – in contrast to the dramatic increase in Clade 4. In Clades 5 and 6,

chap-12 4/6/2004 17: 27 page 301

DISPARITY AND VARIATION 301

Pygopristis denticulat

S. gouldingi

S. manueli

S. elongatus

Pygocentrus piraya

P. nattereri

P. cariba

S. spilopleura

Serrasalmus altuvei

Figure 12.3 Cladogram of the piranhas analyzed in this chapter; nodes are numbered to designate

clades.

Table 12.1 Disparities of clades (numbered as in Figure 12.3), measured at two ontogenetic stages

(disparities of juveniles are measured at the transition from larval to juvenile growth; those of adults

are measured at maximum body size attained by each species)

Taxon Juvenile disparity Standard error Adult disparity Standard error

Clade 1 0.00543 0.0003 0.00398 0.0002

Clade 2 0.00575 0.0003 0.00405 0.0002

Clade 3 0.00431 0.0004 0.00550 0.0003

Clade 4 0.00229 0.0002 0.00603 0.0004

Clade 5 0.00116 0.0002 0.00151 0.0001

Clade 6 0.00073 0.0002 0.00051 0.0002

disparity is constant throughout ontogeny. A perhaps counterintuitive result is that adult

disparities of Clades 3 and 4 are significantly greater than that of the group as a whole

(Clade 1), which may seem impossible, but disparities measured this way are not additive.

In these analyses, we are measuring the disparity of each clade relative to that clade’s own

mean – hence a low disparity indicates that few species differ by much from the mean of that

clade. Consequently, a group comprising three or four species that differ a great deal from

each other (and from the group mean) can have a much higher disparity than a larger group

that includes those species. That is because the additional species in the larger group may all

be much closer to the grand mean. Consequently, their values of D

are small and contribute

relatively less to



, whereas the addition of each species increases N −1 by one.

chap-12 4/6/2004 17: 27 page 302

302 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Table 12.2 Partial disparities (PD) of adults, and the standard

errors of PD

Species PD % MD Standard error

P. denticulata 0.00039 9.82 0.00032

S. elongatus 0.00144 36.27 0.00029

S. gouldingi 0.00026 6.55 0.00031

S. manueli 0.00033 8.31 0.00032

S. altuvei 0.00014 3.53 0.00032

S. spilopleura 0.00023 5.79 0.00032

P. cariba 0.00036 9.07 0.00028

P. nattereri 0.00039 9.82 0.00027

P. piraya 0.00043 10.83 0.00031

The net effect is that MD decreases. For that reason, a large group containing only a

few species that are far from the grand mean can be less disparate than a small group with

the same number of species far from the mean. That is one reason why morphological

disparity can decrease while taxonomic diversity increases.

Partial disparity

When we want to quantify the contribution that a particular taxon makes to the overall

disparity of a larger group, we want a metric that allows us to partition disparity additively.

Therefore, we need an alternative to the method discussed above. The alternative does

allow us to estimate partial disparity (PD) of the species, and the partial disparities sum to

the total disparity. We estimate partial disparities (PD), following the procedure outlined

by Foote (1993a), in terms of the variance contributed by each individual species:

PD =

N − 1

(12.5)

where D

is the distance of the ith species from the grand mean and N is the total number

of species (or other groups). If we wish to calculate the partial disparity of several species

(e.g. a subclade in a larger clade) we can sum their individual partial disparities, yielding

the partial disparity of that group.

We can see the difference between the two approaches by comparing results (for adults)

in Tables 12.1 and 12.2. The total disparity over all nine species (Clade 1) is the same for

both. By estimating the partial disparities for all the species, we can determine that the par-

tial disparity of Clade 4 is 0.00203, which is 52.6% of the total. The partial disparity of a

single species, S. elongatus, accounts for 36.3% of the total disparity of adults of these nine

species. Quantifying partial disparities is one method for estimating the phenotypic distinct-

ness of a particular taxon, which may have a practical application in conservation biology.

Variation

Studies of variation, like those of disparity, use a variance as a metric. The major computa-

tional difference between analyses of disparity and variance are that (1) studies of variance

chap-12 4/6/2004 17: 27 page 303

DISPARITY AND VARIATION 303

use the mean of a single homogeneous population as the grand mean, and (2) individuals

(rather than mean shapes of species) are the data points in studies of variance. One quick

method for estimating the variance in shape is to calculate the variance for all the coor-

dinates obtained by a GLS superimposition and sum those variances over all landmarks

(this is exactly the same as calculating the trace of the variance–covariance matrix, and

can be done in any spreadsheet). This method, while quick and intuitive, will not provide

confidence intervals. It can also be risky if it leads to thinking of variances as being at land-

marks (recall that changes in relative landmark positions are distributed across landmarks,

a topic discussed in context of superimposition methods, Chapter 3). Just as change is not

located at a landmark, neither is variance.

We exemplify an analysis of the ontogeny of variation by comparing the variance of

skull shape across four ages, 10-, 15-, 20-, and 25-days postnatal, of the house mouse

(Mus musculus domesticus). The superimposed landmarks for each sample are shown in

Figure 12.4; the estimates for the variance in shape at each age, and standard errors of

the estimate, are given in Table 12.3. To compare the levels of variance between suc-

cessive ages, we again use the t-test to evaluate the difference between variances relative

to the pooled standard errors of those variances (the same procedure discussed above

for comparing levels of disparity). Over the initial 5-day interval variance is halved, but

it is subsequently stable. The loss of variance, in the absence of any selective deaths in

the colony, indicates that variation is developmentally regulated and the later stability of

the variance also suggests canalization because we would expect continued production of

variation by the ongoing process of skeletal development.

Analyzing the structure of disparity

To this point we have talked solely about the magnitudes of disparity and variance; in this

section, we discuss methods for analyzing their structure. We address two questions about

that structure:

1. Are shapes randomly distributed throughout the morphospace?

2. Do two samples occupy the same subspace?

The first question is answered using nearest-neighbor analysis, the second by comparing

occupied subspaces or variance–covariance matrices.

Nearest-neighbor analysis

Nearest-neighbor analysis, as the term implies, examines the smallest distances between

shapes. From those distances, we can ask whether shapes are more (or less) similar than

expected by chance. If they are closer than expected by chance, we would reject the null

hypothesis in favor of one of clustering; conversely, if they are further apart than expected

by chance, we would reject the null model in favor of a hypothesis of “over-dispersion” (or

“repulsion”). Because the null model is the distribution expected by chance, it is important

to consider what the reasonable null model might be. One reasonable null model is that the

probability of being at any location in the morphospace is equal (uniform) over the entire

space, and is independent of the shape of any other species. Another reasonable null model

chap-12 4/6/2004 17: 27 page 304

304 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(D)

(C)

(B)

Figure 12.4 Superimposed landmarks of M. m. domesticus: (A) 10-day-olds; (B) 15-day-olds;

Table 12.3 Skull shape variance of M. m. domesticus sam-

pled at four ages (given in days after birth), and the standard

errors of the variance (the superimposed landmarks are shown

in Figure 12.4)

Age Variance Standard error

10 0.000628 0.0001

15 0.000349 0.00005

20 0.000316 0.0001

25 0.000410 0.0001

chap-12 4/6/2004 17: 27 page 305

DISPARITY AND VARIATION 305

is that shapes follow a normal (Gaussian) distribution. The uniform model is a reasonable

null for comparisons among species, whereas the Gaussian model is more reasonable when

analyzing distributions of individuals around the mean of a homogeneous sample. Having

two null models allows us to guard against accepting a hypothesis of a particular random

distribution.

Nearest-neighbor analysis is another method pioneered by Foote (1990), so we begin

by reviewing his approach, and then we extend it to geometric shape data.

Foote’s approach to nearest-neighbor analysis The first step in a nearest-neighbor analysis

is to compute the nearest-neighbor distance D

for each of the N species (or other groups)

in the study. For the sake of brevity, we will refer to “species” as the units of analysis,

but the analysis follows the same protocol even when the units are individual specimens.

The next step is to construct a second data set using Monte Carlo simulations. That is

done by estimating the mean and range of each variable; from the data, N −1 simulated

specimens are generated with values randomly drawn from the observed range. Monte

Carlo simulations are similar to bootstraps in that they simulate data based on a given null

model and an observed set of data, but they differ in that bootstrapping is carried out using

a non-parametric resampling procedure whereas Monte Carlo simulations are based on a

distributional model. The distribution of the original data set is parameterized, and those

parameters are used to generate a simulated dataset having the distribution of the obser-

vations (see Chapter 8). Given the simulated data, a second nearest-neighbor distance, R

is computed between each observed specimen and the one closest to it in the Monte Carlo

set (note that R

is not a nearest-neighbor distance between Monte Carlo specimens, but

rather the distance between an observed specimen and the nearest Monte Carlo simulated

specimen).

Foote provides a measure that allows us to compare the fit of the simulated distances to

the observed ones, the proportional distance P

for the ith specimen. This is a ratio whose

numerator is the difference between the two distances (D

, the observed nearest neighbor

distance, and R

, the Monte Carlo nearest neighbor distance) and whose denominator is

the Monte Carlo nearest neighbor difference:

−R

(12.6)

If the random model fits the data, we would expect that, on average, D

would equal

, and hence the mean P

over all specimens (P

mean

) is zero. When P

mean

is less than zero

the observed specimens are more clustered than expected by chance; conversely, if P

mean

is greater than zero they are further apart than expected by chance. To determine whether

zero lies within the confidence interval, we estimate the range of P

mean

by running the

Monte Carlo simulation many times.

To generate a Monte Carlo set under a multivariate normal (Gaussian) model, we must

estimate the mean and standard deviation of each variable; to generate a Monte Carlo

set under a uniform distribution model, we must estimate the upper and lower bounds

of the range for each variable. It can be difficult to estimate the range accurately when

sample sizes are small because, at small sample sizes, the observed minimum and maximum

will underestimate the “true” range. Thus, rather than using the observed minimum and

maximum values to estimate the range, Foote uses estimators developed by Strauss and

chap-12 4/6/2004 17: 27 page 306

306 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Sadler (1989) for the “true” minimum (Y) and the “true” maximum (Z) of a distribution:

Y =

NA −B

N − 1

(12.7)

Z =

NB −A

N − 1

(12.8)

where A is the lowest observed value and B is the highest observed value in N specimens.

Rather than use the observed minimum and maximum values, Foote determines the mean

and the standard deviation of a normal distribution fitted to the data. He uses normal

theory (citing Feller, 1968) to predict the mean and standard deviation:

mean

= Y +

(Z − Y)

(12.9)



(Z − Y)



(12.10)

and he uses those to estimate the range parameters:

Y = X

mean

−3

(12.11)

Z = X

mean

(12.12)

The geometric approach to nearest-neighbor analysis Extending nearest-neighbor analy-

sis to geometric data is straightforward. Distances D

and R

are measured by Procrustes

distance; estimates of means, standard deviations or ranges used in the Monte Carlo sim-

ulation are obtained by calculating the statistics from the coordinates of each landmark.

The rest is straightforward: a Monte Carlo data set is generated and R

is calculated for

each specimen, and these are used to estimate P

mean

. The simulation is reiterated numer-

ous times, yielding the distribution of P

mean

values over the Monte Carlo sets. It is then

possible to carry out all the usual statistical tests using this distribution.

Nearest-neighbor analysis of piranha disparity

We will test two hypotheses:

1. Piranha body shapes, both juvenile and adult, are further apart than expected.

2. Those shapes are more clumped than expected.

The reason for testing these hypotheses separately is that a conservative test of one is a

liberal test of the other. For the hypothesis of over-dispersion, the conservative approach

uses the Strauss and Sadler estimator of the range – the estimator enlarges the range so

that large distances between points will not necessarily be further apart than expected.

However, that expansion of the range can lead to a liberal test of clumping because, within

that expanded range, observations may be closer than expected. To be conservative, we

would test the hypothesis of over-dispersion using the enlarged range, but we would use

parameters of the observed range to test a hypothesis of clustering. Each hypothesis will

be tested using two null models, one uniform and the other Gaussian, because we have no

good reason to view one as a more plausible random model.

chap-12 4/6/2004 17: 27 page 307

DISPARITY AND VARIATION 307

Testing over-dispersion Using the uniform model, the average P

mean

of the juveniles is

−0.2810 and the 95% range of P

mean

is from −0.3551 to −0.1792, an interval that

excludes zero. This result suggests a non-random distribution, with distances being smaller

than expected under a random uniform model. Using the Gaussian model, the average

mean

=−0.2758 and its range is from −0.3450 to −0.1950, an interval that again excludes

zero. Both results thus argue against the hypothesis of a random distribution and also

against over-dispersion. Instead they suggest clustering, the hypothesis we will explicitly

test after we have tested the hypothesis of over-dispersion for adults.

Using the uniform null model, the average P

mean

of the adults is −0.267 and the range

is from −0.3365 to −0.1689, an interval that excludes zero. This result also suggests

a non-random distribution, with distances being smaller than expected under a random

uniform model. Using the Gaussian model, the average P

mean

=−0.2636 and the range

is from −0.3312 to −0.2036, an interval that also excludes zero. As we found for the

juveniles, the data argue against the null hypothesis of a random distribution, and also

against over-dispersion. Therefore, we now explicitly test the hypothesis of clustering.

Testing clustering We now test the hypothesis of clustering using the narrower estimate

of the range. For the juveniles, based on the uniform model, the average P

mean

=−0.3172

with a range from −0.3813 to −0.2247, an interval that excludes zero and supports the

hypothesis of clustering. Analyzing the data under the null Gaussian model, the average

mean

=−0.3006 with a range from −0.3700 to −0.2372, an interval that again excludes

zero. Taking these results altogether, they suggest that juvenile piranha body shapes are

more tightly clustered than expected under either null model.

For the adults, using the uniform null model, the average P

mean

=−0.2537 with a range

from −0.3092 to −0.1788, an interval that excludes zero. These results again support the

inference of clustering. Analyzing the data under the Gaussian null model, the average

mean

=−0.2388 with a range from −0.3091 to −0.1598, an interval that once again

excludes zero. Taking these results altogether, they suggest that adult piranha body shapes

are more tightly clustered than expected under either null model.

While both developmental stages seem to exhibit clustering, that does not mean that they

are otherwise similar in their patterns of disparity. Later in this chapter we will compare

the subspaces of morphospace they occupy to determine if they are the same.

Nearest-neighbor analysis of 10-day-old house mouse skull shape variation

Nearest-neighbor analysis can be used to examine patterns of variation as well as disparity.

To exemplify this, we will analyze the variation in 10-, 15-, 20- and 25-day-old mouse

skulls. The superimposed landmarks for these ages were shown in Figure 12.4. Considering

that each sample comprises individuals from a single homogeneous population, we would

expect random variation to follow a Gaussian distribution. Results of analyses based on

both range estimators (i.e. the parameter values estimated using the Strauss–Sadler estimate

of the range (SS), and those estimated from the data (DP)) are given in Table 12.4. It is

difficult to argue that the data suggest a departure from random variation. When the

parameter estimates are based on an expanded range, the two youngest samples seem

to be more clustered than expected under the null hypothesis of a Gaussian distribution.

That expansion seems appropriate in light of the small sample sizes, but using it could be