Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

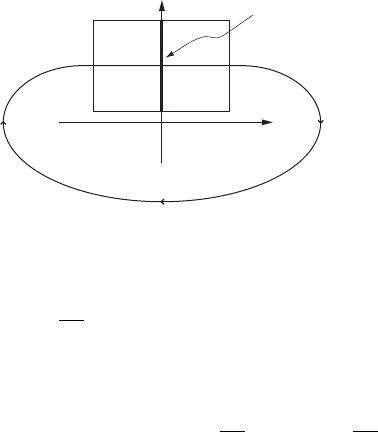
VIII.4. Poincaré’s continuation method 331

D 0g

†



x.t/

Figure VIII.9. The local situation in the coordinates x D .x

;:::;x

in which p D 0 2 R

and

.0/ ¤ 0 using that dH ¤ 0. In these coordinates

we introduce the function F W R

 R ! R deﬁned by

F.y;E/ D H.y/  E:

It satisﬁes F .0; E



/ D H.0/  E



D 0 and

F .0; E/ D

.0/ ¤ 0. The

implicit function theorem guarantees a unique function

D f.E;y

;:::;y

/ D f.E;y

/; y

´ .y

;:::;y

solving the equations



f.E;y

/; y



D H



f.E;y

/; y



 E D 0;

f.E



;0/D 0:

Near y D 0 we introduce the new coordinates x D .x

;:::;x

/ D .x

by means of the local diffeomorphism

y D .y

/ D '.x/ D .f .x

/; x

where x

D E and x

D y

. In the new coordinates, the function H has the

desired representation

H.x/ D H



f.x

/; x



D H



f.E;y

/; y



D E D x

For the function

H we shall again write H . From H.x/ D x

we deduce

0 D dH.X

/ D dx

/ D

;

where

is the ﬁrst component of the vector ﬁeld. Since X

¤ 0 near

p D .E



;0/, we can assume without loss of generality that

¤ 0:

332 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

Therefore, the set fx j x

D 0g represents a local transversal section of x.t/

near .E



;0/and the coordinates .x

;:::;x

/ have the desired properties (i), (ii)

and (iii).

Recall that H.'

.x// D H.x/ for all x 2 M . Then the transversal map

W † ! †; † Dfx j x

D 0g

has, in the local coordinates

x D .x

/ 2 †; x

D x

D .x

;:::;x

2n1

and considering the energy conservation

D x

D H.x/ D H.'

.x/

.x// D H. .x// D . .x//

.x/;

the representation













We are looking for ﬁxed points of the map near the ﬁxed point .E



;0/ D



;0/, that is, for points .x

/ satisfying

The ﬁrst equation has already been solved by our choice of the coordinates. The

second equation,

/  x

D 0;

possesses the solution .x

/ D .E



;0/, so that



;0/ 0 D 0:

In view of

/ D x

, the linearized map at the point x



´ .E



;0/has the

form

d .x



/ D







By assumption, the linear map d'



/ has precisely two eigenvalues equal

to 1. From Proposition VIII.13 it therefore follows that 1 is not an eigenvalue of

the matrix



/, so that the linear map



/  1

2n2

VIII.5. Transversal sections on energy surfaces 333

is an isomorphism. The implicit function theorem, therefore, guarantees a unique

smooth function x

D a.x

/ satisfying a.E



/ D 0 and

;a.x

//  a.x

/ D 0;

for x

D E near E



. We have constructed a smooth family .E; a.E// 2 † of ﬁxed

points of the section map W † ! † for energies E close to E



. These ﬁxed

points are the initial conditions of the desired periodic solutions having energies

E near E



and periods T D .x/ near T



. In addition, these solutions are the

only such solutions near the reference solution. The proof of Theorem VIII.14 is

complete. 

We see that typically, in (time independent) Hamiltonian systems the periodic

solutions appear in 1-parameter families, parametrized by the energies and having

similar periods. On the other hand, on a ﬁxed energy surface the periodic solutions

are isolated among the periodic solutions having similar periods.

This applies not only to Hamiltonian vector ﬁelds. The same statements hold

true for every time independent vector ﬁeld X, possessing a regular integral F .

All one needs to do is to replace in the proof the Hamiltonian function H by the

integral F .

VIII.5 Transversal sections on energy surfaces

As in the previous section, we consider a periodic solution x.t/ of the Hamiltonian

vector ﬁeld Px D X

.x/ on the symplectic manifold .M; !/ having the energy

E D H.x.t//, and we assume that the energy surface

S Dfx 2 M j H.x/ D Eg

is regular and hence a submanifold of dimension 2n 1.If†  M is a transversal

section of the periodic orbit x.t/, it follows from the energy conservation that the

section map D '



W † ! † leaves the energy surface invariant,

W † \ S ! † \ S:

We can, therefore, introduce the transversal sections †

on the energy surface S

and the associated restricted section map by

†

´ † \ S and W †

! †

Theorem VIII.14. The transversal section †

D † \ S of the periodic solution

x.t/ in the energy surface S is a symplectic submanifold of .M; !/ of dimension

2n  2 equipped with the symplectic form !

D !j

†

D j



!, where j W †

! M

is the inclusion map. The transversal section map W †

! †

is symplectic and

hence satisﬁes



D !

334 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

Proof. (1) We ﬁrst show that !

is a symplectic form. The 2-form !

is, of course,

closed, because dj



! D j



d! D 0 and we have to show that !

is nondegenerate.

We recall that the tangent space of S has the representation

S D ker dH.x/ D ker !.X

; / Df 2 T

M j !.X

;/ D 0g:

Since †

in S is transversal to X

S D T

†

˚ spanfX

.x/g:

Assuming that the tangent vector v 2 T

†

satisﬁes

!.v; u/ D 0 for all u 2 T

†

;

we shall show that v D 0. The tangent vector  2 T

S has the representation

 D u C˛X

for an ˛ 2 R and a tangent vector u 2 T

†

. In view of †

 S and

using the deﬁnition of a Hamiltonian vector ﬁeld, we conclude that

!.v; / D !.v; u/ C ˛!.v; X

.x// D 0 C 0:

This holds true for every tangent vector  2 T

S, so that v lies in the 1-dimensional

subspace ker.!j

/ D spanfX

g. Since v 2 T

†

and X

… T

†

we conclude

that v D 0. Consequently, !

D !j

†

is nondegenerate.

(2) It remains to verify that



D !

, explicitly,

!.; / D !



d .x/; d .x/



for all ;  2 T

†

We recall that

d .x/ D

.x/

.x/ D X



.x//d  .x/ C d'



.x/

for  D .x/. Since d'



.x/ is symplectic, it follows, abbreviating l ´ d .x/ and

y ´ '



.x/, for all ; 2 T

†

!.; / D !





.x/; d'



.x/



D !



d .x/  l./ X

.y/; d .x/  l./ X

.y/



D !



d .x/; d .x/



We have used that !.X

.y/; d .x// D 0, in view of d .x/ 2 T

†

 T

and similarly for . 

Example. If dim M D 4, the energy surface S has dimension 3 and the transversal

section †

on S has dimension dim †

D 2. Near p D x.0/ 2 †

we choose a

Darboux chart for †

in which the symplectic structure !

of †

has the form

D dy ^ dx:

VIII.5. Transversal sections on energy surfaces 335

In these local coordinates the transversal map W †

! †

is an area preserving

local diffeomorphism in the plane R

near the ﬁxed point .p/ D p D x.0/ 2 R

Instead of studying the solutions of the Hamiltonian vector ﬁeld X

on the

energy surface S near the periodic reference solution x.t/ for all times, we can as

well study the map and all its iterates on †

By the spectral theorem for linear symplectic maps the Floquet multipliers of

x.t/ are given by

f1; 1; ; 

1

where  and 

1

are the eigenvalues of the linearization d .p/. Assuming, for

example, that  is real and that jj¤1, we conclude that p is a hyperbolic ﬁxed

point of the map . Therefore, the periodic solution x.t/ is unstable on S, in view

of the hyperbolic phenomena described in Chapters II and III.

p D .p/

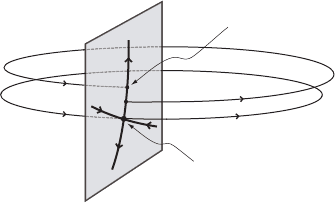
.x/

†

Figure VIII.10. Hyperbolic ﬁxed point p of the section map with invariant manifolds on

†

. The whole picture is contained in the energy surface S .

We next study the relation between Floquet multipliers and integrals for a vector

ﬁeld X which is not necessarily a Hamiltonian vector ﬁeld. We look at the periodic

solution x.t/ having period T>0of the vector ﬁeld on the manifold M of dimen-

sion dim M D n and denote by '

the ﬂow of X. We assume that the vector ﬁeld

X possesses r smooth integrals

W M ! R;˛D 1;:::;r;

in a neighborhood of the periodic solution x.t/, so that dG

.X/ D 0 and hence

.x// D G

.x/; ˛ D 1;:::;r

for all x near x.t/ and all times t as long as the ﬂow is deﬁned. We assume that

the integrals are independent, assuming that the 1-forms dG

.x/ D 0 are linearly

independent. The integral surfaces

N D N

Dfx 2 M j G.x/ D cg

336 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

where G is the map deﬁned by G D .G

;:::;G

/ and where c D .c

;:::;c

/, are

invariant under the ﬂow and of dimension

dim N

D n  r:

At the point x in the integral surface N

the tangent space is equal to

D ker dG.x/:

In particular, X.x/ 2 T

.Ifˆ ´ d'

.p/ is the linearized map at the point p

belonging to the periodic solution x.t/, then

.ˆ/ D dG

./

for all  2 T

M and therefore

ˆ.T

N/ D T

N being the integral surface of the periodic orbit x.t/. In order to compute the

eigenvalues of ˆ we choose local coordinates in a neighborhood of x.0/ in which

the integrals

.x/ D x

for all ˛ D 1;2;:::;r;

become coordinate functions. If we split the coordinates x D .x

;:::;x

/ into

D .x

;:::;x

/ and x

D .x

rC1

;:::;x

/, the map ˆ has, with respect to this

splitting, the form

ˆ D







where

ˆ D ˆj

is the restriction of ˆ to the tangent space T

N .Wenow

proceed as before by considering the ﬂow '

of the vector ﬁeld X restricted to the

integral surface N . Clearly,

ˆX.p/ D X.p/

and choosing a transversal section †  N in the integral surface N , we ﬁnd with

respect to the splitting

D spanfX.p/g˚T

†

the representation of

ˆ as the .n  r/  .n  r/-matrix

ˆ D

l

d .p/

From this matrix we read off the following theorem.

VIII.5. Transversal sections on energy surfaces 337

Theorem VIII.15. We consider a non-constant periodic solution x.t/ of the vector

ﬁeld X on the manifold M .IfX possesses r independent integrals near x.t/, then

r C 1 Floquet multipliers of x.t/ are equal to 1. The other Floquet multipliers

are the eigenvalues of the derivative d .x.0// of the section map W † ! †

of a transversal section †  N

of x.t/, where N

is the integral surface on

which x.t/ lies. The characteristic polynomials are related by det.  ˆ/ D

.  1/

rC1

det.  d .x.0//.

Analogous to the proof of Theorem VIII.14, we can introduce new coordinates

x D .x

/ in which the integrals G.x

/ D x

become coordinate functions

and fx j x

D 0gR

deﬁnes a local transversal section. Solving the ﬁxed point

equation x D .x/ near the reference solution by means of the implicit function

theorem, we obtain the following result.

Theorem VIII.16. We assume that the vector ﬁeld X on the manifold M possesses

r independent integrals G

;;G

near a given periodic solution x.t;c



/ of period



>0which lies on the integral surface N



Dfx 2 M j G.x/ D c



g for the

map G D .G

;;G

/ and for the constants c



2 R

If x.t/has exactly r C1 Floquet multipliers equal to 1, then there exists a smooth

r-parameter family x.t;c/ of periodic solutions for c near c



having periods T.c/

near T



D T.c



/. They are parametrized by the integral values c D G.x.t;c// 2

. In view of these properties, the family is unique. The periods T.c/ depend

smoothly on the parameter c. In particular, T.c/ ! T



as c ! c



Geometrically the family forms an embedded (generalized) cylinder S

 B

where B

 R

is an open ball.

As a side remark we observe that an additional integral of a Hamiltonian vector

ﬁeld X

frequently gives rise to two Floquet multipliers equal to 1 and not just

one, so that the assumptions of Theorem VIII.16 are not met. In this case we cannot

apply the continuation method used above in order to ﬁnd periodic orbits.

Proposition VIII.17. Suppose that the Hamiltonian vector ﬁeld X

on the sym-

plectic manifold .M; !/ possesses the r integrals H

for 1  ˛  r, that is,

gD0;

and assume that the 1-forms dH

are linearly independent. If, at some point p

contained in the periodic solution x.t/ of the Hamiltonian vector ﬁeld X

,we

have

g.p/ D 0 for 1  ˛  r and 1  ˇ  s;

for some s  r, then the periodic orbit x.t/ has r C s Floquet multipliers equal

to 1.

338 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

Proof. Introducing locally near the point p the integrals as coordinates, in the

notation of Theorem VIII.17 we have

ˆ D







;

where

ˆ D ˆj

, the manifold N being the integral surface of the periodic

solution x.t/ whose tangent space at the point p is equal to

N Df 2 T

N j !.X

;/ D 0; for ˛ D 1;2;:::;rg:

It sufﬁces to prove that the matrix

ˆ has s eigenvalues equal to 1 belonging to the

eigenvectors X

for 1  ˛  s. Since

ŒX

 D X

D 0;

the ﬂow '

of X

and the ﬂow

of X

.p/ do commute, so that

B '

Differentiating in s at s D 0 gives

.p/ X

.p/ D X

.p//:

Hence, if t D T is the period of the periodic solution x.t/,

ˆ.X

.p// D X

.p/

for every ˛ D 1;2;:::;r. It remains to prove that

.p/ 2 T

N D

˛D1

ker dH

.p/

for all 1  ˇ  s. But this is precisely our second assumption, because at the

point p,

/ D !.X

/ DfH

gD0

for all 1  ˛  r and 1  ˇ  s. The proof of PropositionVIII.17 is complete. 

From Proposition VIII.17 we conclude in particular that all the 2n Floquet

multipliers of a periodic solution of an integrable Hamiltonian system are equal

to 1. This situation is, of course, not stable under a perturbation.

Literature. Chapter VIII is, like Chapter VII, also partly based on the book [52]

by H. Hofer and E. Zehnder and makes use of the notes on dynamical systems [74]

by J. Moser and E. Zehnder. For a recent account of the problem of periodic orbits

of Hamiltonian systems having prescribed energies, we refer to [41] and [42]by

V. Ginzburg.

Bibliography

The numbers at the end of each item refer to the pages on which the respective work is cited.

[1] A. Abbondandolo, Morse theory for Hamiltonian systems. Chapman and Hall/CRC,

Boca Raton, Fl., 2001. 181

[2] R. Abraham and J. Marsden, Foundations of mechanics. 2nd edition. The Benjamin

Cummings Publishing Company, Inc., Reading, Mass., 1978. 238

[3] S. Alpern and V. S. Prasad, Typical dynamics of volume preserving homeomorphisms.

Cambridge Tracts in Math. 139, Cambridge University Press, Cambridge, 2000.

[4] H. Amann, Lectures on some ﬁxed point theorems. IMPA monograﬁas de matemátika.

299

[5] H. Amann, Ordinary differential equations. De Gruyter Stud. Math. 13, Walter de

Gruter, Berlin, 1990. 80, 127, 130, 148, 299

[6] K. G. Anderson, Poincaré’s discovery of homoclinic points. Arch. History Exact Sci.

48 (2) (1994), 113–147. 80

[7] D. V. Anosov, Geodesic ﬂows on closed Riemann manifolds with negative curvature.

Trudy Mat. Inst. Steklov 90, 1967; English translation in Proc. Steklov Inst. Math. 90,

Amer. Math. Soc., Providence, RI, 1969. 126

[8] V. I.Arnold andA.Avez, Ergodic problems of classical mechanics.Adv. Book Classics,

Addison-Wesley, Redwood City, Cal., 1989. 237, 238

[9] A. Banyaga and B. Hurtubise, Lectures on Morse homology. Kluwer Academic Pub-

lishers, Dordrecht, 2004. 180

[10] M. Berger and B. Gostiaux, Differential geometry: manifolds, curves, and surfaces.

Grad. Texts in Math. 115, Springer-Verlag, New York, 1988.

[11] S. V. Bolotin, Libration motions of natural dynamical systems. Moscow Univ. Math.

Bull. 33 (1978), 49–53. 327

[12] R. Bott, Lectures on Morse theory, old and new. Bull. Amer. Math. Soc. (N.S.) 7 (1982),

331–358. 181

[13] R. F. Brown, A topological introduction to nonlinear analysis. Birkhäuser, Boston,

Mass., 1993. 299

[14] K. C. Chang, Inﬁnite dimensional Morse theory and multiple solution problems. Progr.

Nonlinear Differential Equations Appl. 6, Birkhäuser, Boston, Mass., 1993. 181

[15] M. Chaperon, Stable manifolds and the Perron-Irwin method. In Dynamical systems,

ed. by A. Fathi and J.-C. Yoccoz, Cambridge University Press, 2006, Cambridge,

89–124. 80

[16] M. Chaperon, Invariant manifold theory via generating maps. C. R. Acad. Sci. Paris,

Ser. I 346 (2008), 1175–1180. 80

340 Bibliography

[17] A. Chenciner, Le dynamique au voisinage d’un point ﬁxe elliptique conservatif: de

Poincaré et Birkhoff à Aubry et Mather. Séminaire Bourbaki, Astérisque 121/122

(1984), 147–170. 238

[18] K. Cieliebak, H. Hofer, J. Latschev and F. Schlenk, Quantitative symplectic geometry.

In Dynamics, ergodic theory, and geometry, Math. Sci. Res. Inst. Publ. 54, Cambridge

University Press, Cambridge, 2007, 1–44. 306

[19] C. Conley, Isolated invariant sets and the Morse index. CBMS Reg. Conf. Ser. in

Math. 38, Amer. Math. Soc., Providence, RI, 1978. 181

[20] C. Conley and E. Zehnder, Morse-type index theory for ﬂows and periodic solutions

for Hamiltonian equations. Comm. Pure Appl. Math. 37 (1984), 207–253. 181

[21] L. Conlon, Differentiable manifolds. 2nd edition, Birkhäuser Adv. Texts, Birkhäuser,

Boston, Mass., 2001. 164, 180, 206, 229

[22] O. Cornea, G. Lupton, J. Oprea, and D. Tanré, Lusternik–Schnirelman category. Math.

Surveys Monogr. 103, Amer. Math. Soc., Providence, RI, 2003. 160, 161

[23] I. P. Cornfeld, S. V. Fomin, and Ya. G. Sinai, Ergodic theory. Grundlehren Math. Wiss.

245, Springer-Verlag, Berlin, 1982. 45

[24] R. H. Cushman and L. M. Bates, Global aspects of classical integrable systems. Birk-

häuser, Basel, 1997. 194

[25] B. Dacorogna and J. Moser, On a partial differential equation involving the Jacobian

determinant. Ann. Inst. H. Poincaré Anal. Non Linéaire 7 (1) (1990) 1–26. 240

[26] K. Deimling, Nonlinear functional analysis. Springer-Verlag, Berlin, 1985. 159, 160,

161, 299

[27] R. L. Devaney, An introduction to chaotic dynamical systems. 2nd edition, Stud.

Nonlinearity, Westview Press, Boulder, CO, 2003.

[28] A. Dold, Lectures on algebraic topology. 2nd edition, Grundlehren Math. Wiss. 200,

Springer-Verlag, Berlin, 1980.

[29] J. Duistermaat, Stable manifolds. Preprint No. 40, Department of Mathematics, Uni-

versity of Utrecht, 1976. 80

[30] J. Duistermaat, Fourier integral operators. Progr. Math. 130, Birkhäuser Verlag,

Boston, Mass., 1996. 238

[31] H. Dym and H. P. McKean, Fourier series and integrals. 2nd print., Academic Press,

New York, 1974. 35

[32] R. W. Easton, Geometric methods for discrete dynamical systems. Oxford Engrg. Sci.

Ser. 50, Oxford University Press, New York, 1998.

[33] I. Ekeland and H. Hofer, Symplectic topology and Hamiltonian dynamics. Math. Z.

200 (1989), 355–378. 252

[34] I. Ekeland and H. Hofer, Symplectic topology and Hamiltonian dynamics II. Math. Z.

203 (1990), 553–567. 252

[35] B. Fiedler (ed.), Handbook of dynamical systems

. Vol. 2, North-Holland, Amsterdam,

2002. 45