Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

VII.4. The functional analysis of the action functional 291

The vector ﬁeld rˆW E ! E is globally Lipschitz-continuous. Indeed, rˆ D

ra rb where ra D .P

 P



/ is a bounded linear operator and where rb is

Lipschitz-continuous by Proposition VII.23. Thus, the gradient equation

Px Drˆ.x/; x 2 E

generates a global ﬂow '

.x/ which is deﬁned for all x 2 E and t 2 R. The map

' W R  E ! E; .t; x/ ! '

.x/ μ x  t

maps bounded sets onto bounded sets and possesses, in addition, the following

compactness property.

Proposition VII.26 (Representation formula for the ﬂow). The ﬂow '

.x/ of the

gradient equation Px Drˆ.x/ on E has the representation

.x/ D e



C x

C e

t

C K.t; x/

for all t 2 R and all x D x



2 E, where the rest term K W R E ! E

is a compact map, that is, it maps bounded sets onto relatively compact sets.

Proof [Duhamel’s variation of the constants formula]. The ﬂow '

.x/ of a Lip-

schitz-continuous ordinary differential equation in E of the form

Px D Ax C f.x/

where A 2 L.E/ satisﬁes the formula

.x/ D e

x C

.ts/A

f.'

.x// ds:

Indeed, the right-hand side, denoted by .t/, solves the equation

 D A.t / C

f.'

.x// and the initial condition .0/ D x, as can easily be veriﬁed. Because the

ﬂow '

.x/ solves the same initial value problem, the uniqueness of the solution

implies that .t/ D '

.x/. Applied to our gradient equation

Px Drˆ.x/ D .P



 P

/x Crb.x/

we obtain for the ﬂow '

.x/ the desired representation formula with the rest term

K deﬁned by

K.t; x/ ´



ts



C P

C e

tCs



rb.'

.x// ds:

We have used that if x D x



C x

2 E, then, in view of the orthogonality

of the projectors,

t.P



P

x D e

t.P



P



C P

D .e



C P

C e

t

D e



C x

C e

t

292 Chapter VII. Symplectic invariants

It remains to verify that K.t; x/ is a compact map. Recalling

rb.x  s/ D j



rH.j.x  s//

where j



2 L.L

;E/and x  s D '

.x/, we can write the map K as

K.t; x/ D j





ts



C P

C e

tCs



rH.j.x  s// ds



We see that the map K is the composition of a continuous, bounded map RE ! L

with the compact map j



W L

! E, so that K is also a continuous and compact

mapping, as claimed in the proposition. 

VII.5 Existence of a critical point of ˆ

In this section we ﬁnally establish a critical point x of the function ˆ W E ! R

which satisﬁes ˆ.x/ > 0 by means of a special minimax argument.

Let us brieﬂy recall our strategy. We started with the action functional ˆW  D

; R

/ ! R of classical mechanics,

ˆ.x/ D

hJ Px; xidt 

H.x.t//dt

having the formal L

gradient

rˆ.x/ DJ Px rH.x/:

The functional ˆ wasextended to a continuously differentiablefunction ˆ W E !

R, deﬁned on the Hilbert space E D H

  by

ˆ.x/ D a.x/  b.x/ D







H.x.t//dt

where kkdenotes the norm of H

and where the splitting x D x



E D E



˚ E

is deﬁned by means of the Fourier coefﬁcients. The E

gradient of ˆ is equal to

rˆ.x/ Dra.x/ rb.x/ D x

 x



 j



rH.j.x//:

The function H 2 C

; R/ is non-negative and has, in addition, the special

properties that H vanishes in a neighborhood of z D 0 and is equal to the quadratic

form

H.z/ D . C "/q.z/; jzjR

outside of a large ball.

VII.5. Existence of a critical point of ˆ 293

We should point out that the functional ˆ W E ! R has many critical points,

but most of them are uninteresting! Examples are the critical points z



of the

Hamiltonian function H W R

! R satisfying rH.z



/ D 0. These points are

constant loops and therefore solve the equation

rˆ.z



/ Dra.z



/  j



rH.z



/ D 0:

Moreover,

ˆ.z



/ D a.z



/  b.z



/ D 0  H.z



/  0:

The goal of this section is the proof of the following result.

Theorem VII.27. There exists a critical point x 2 E satisfying

rˆ.x/ D 0 and ˆ.x/ > 0:

By the regularity theorem (Proposition VII.24) the critical point x belongs to

; R

/ and solves the Hamiltonian equation

Px.t/ D J rH.x.t//:

In view of ˆ.x/ > 0 and by Lemma VII.16 the loop x.t/ is a non-constant 1-pe-

riodic solution, lying in the ellipsoid E  Z.1/ where H D

H agrees with the

original Hamiltonian function. Therefore, Theorem VII.27 above completes the

proof of Theorem VII.15. Consequently, also Theorem VII.10 is herewith proved

and shows that the map

.M; !/ 7! c

.M; !/

is, indeed, a symplectic capacity. Together with the existence proof of the sym-

plectic capacity c

, also all its consequences in symplectic geometry, in particular,

Gromov’s non-squeezing theorem (Theorem VII.5), are proved. We see that all the

results in symplectic geometry so far follow from the existence of a special critical

point of the old action functional of classical mechanics.

Before presenting a detailed proof of Theorem VII.27 we shall brieﬂy sketch

the argument. We deﬁne for   0 the bounded subset † D †



 E by

†



x 2 E j x D x



C x

C se

where kx



C x

k and 0  s  



Here e

2 E

denotes the special loop

.t/ ´ e

2tJ

where e

D .1;0;:::;0/ 2 R

. In addition, we deﬁne for ˛>0the bounded

subset  D 

 E



Dfx 2 E

jkxkD˛g:

It is the sphere of radius ˛ in E

centered at the origin.

294 Chapter VII. Symplectic invariants



˚ E

†

@†



Figure VII.13. The subsets † and  of E.

Lemma VII.28. On the boundary @†



of †



 E



˚ E

˚ Re

the function ˆ

satisﬁes the estimate

ˆj

@†



 0

if >0is sufﬁciently large. In addition, there exist real numbers ˛>0and ˇ>0

such that

ˆj



 ˇ>0:

We postpone the proof of the lemma which uses the pointwise behavior of the

function H .

Continuing with the proof of Theorem VII.27 we now let the set † move under

the gradient ﬂow 

of Px Drˆ.x/. Since the function ˆ.'

.x// is decreasing

in t for t  0, we conclude from Lemma VII.28 not only ˆj

@†

 0, but also

ˆj

.@†/

 0 for all t  0:

It therefore follows from ˆj



 ˇ>0, where  D 

, that

.@†/ \  D; for all t  0:

We see that the deformed frame '

.@†/ never intersects the sphere  for t  0.

On the other hand, the two sets  and † do intersect in the point se

2 † \ 

where s D ˛=ke

k if  is sufﬁciently large. Since the frame '

.@†/ cannot be

pulled through the sphere as t increases, one expects the surface '

.†/, spanned

VII.5. Existence of a critical point of ˆ 295

by the frame, to intersect the sphere for every t  0. This is intuitively quite clear

looking at Figure VII.13 where the sphere is depicted as a circle.

Lemma VII.29 (Topological linking).

.†/ \  ¤;

for all t  0,if>0is sufﬁciently large.

The proof of this lemma will be based on the Leray–Schauder degree. We

postpone it and ﬁrst complete the proof of Theorem VII.27.

Proof of Theorem VII.27 [Lemmata VII.28 and VII.29, Propositions VII.23 and

VII.25, minimax principle]. In order to apply the minimax principle to the function

ˆ on the Hilbert space E we take as family F of sets the following one-parameter

family

.†/; t  0

of subsets of E and deﬁne the minimax

c.ˆ; F/ D inf

t0

sup

x2'

.†/

ˆ.x/:

We verify the assumptions of the minimax principle (Proposition VII.17) and ﬁrst

observe that the family F is positively invariant under the gradient ﬂow, because

of '

.†// D '

sCt

.†/. In view of Proposition VII.25 the functional ˆ satisﬁes

the P.S.-condition and, due to the global Lipschitz continuity, the gradient equation

generates a global ﬂow. It remains to show that c.ˆ; F/ is ﬁnite. Here, the two

lemmata above play a decisive role.

Since '

.†/ \  ¤;for all t  0 by Lemma VII.29, it follows from

Lemma VII.28 that

ˇ  inf

x2

ˆ.x/  inf

x2\'

.†/

ˆ.x/  sup

x2'

.†/

ˆ.x/ < 1

for every t  0. We have used that '

.†/ is a bounded set and that ˆ maps

bounded sets onto bounded sets, in view of Proposition VII.23. Hence c.ˆ;F/ is

a real number so that all the assumptions of the minimax principle are met. The

minimax principle now guarantees a critical point x 2 E satisfying

rˆ.x/ D 0 and ˆ.x/ D c.ˆ;F/  ˇ>0

and Theorem VII.27 is proved. 

It remains to prove Lemma VII.28 and Lemma VII.29.

296 Chapter VII. Symplectic invariants

Proof of Lemma VII.28. The lemma follows from the properties of the Hamiltonian

function H . We recall that

ˆ.x/ D a.x/  b.x/





 b.x/

where b.x/  0. Hence, if x satisﬁes x

D 0, then ˆ.x/  0.

(1) We ﬁrst verify that

ˆj

@†



 0

if  is sufﬁciently large. For this purpose, we use the behavior of the function H

at inﬁnity. On the part @† \ .E



˚ E

/ of the boundary where s D 0,wehave

ˆ  0, as already observed above.

On the other parts of the boundary @†



we have either s D  or kx



kD.

By construction of H there exists a constant   0 such that

H.z/  . C "/q.z/  ; for all z 2 R

and therefore,

ˆ.x/  a.x/  . C "/

q.x/ C ; x 2 E:

If x D x



Cse

2 † we obtain, using the orthogonality of the decomposition

that

q.x



C x

C se

/dt D

q.x



/ C

q.x

/ C

q.se

Since x

is constant and q.x



/  0, one concludes that

ˆ.x/  a.x/. C"/q.x

/. C"/

q.se

/C; x D x



Cse

2 †:

Recalling

D e

2tJ

D cos.2t/e

C sin.2t/Je

D cos.2t/e

 sin.2t/e

nC1

and the deﬁnition of the quadratic form q one sees that

q.se

/ D s

Œcos.2t/

C sin.2t/

 D s

For the next estimate we note that

D 2; ke

D 1

VII.5. Existence of a critical point of ˆ 297

and compute

ˆ.x/ 





 . C "/q.x

/  . C "/

q.se

/ C 

D



 "s

 . C "/q.x

/ C 

   ckx



C x

 ckse

for a constant c>0. In both cases, namely kx



C x

kD and s D  , it follows

that ˆ.x/  0 for sufﬁciently large .

(2) In order to verify the second statement of the lemma,

ˆj



 ˇ>0

for suitable positive numbers ˛; ˇ > 0, we use the behavior of the Hamiltonian

function H near z D 0. Since   E

,wehavea.x/ D

kxk

for x 2 .We

now make use of the following Sobolev estimate, the proof of which can be found

in Appendix C in [52].

Lemma VII.30. The embedding H

 L

/ is continuous for every 1  p<

1. In other words, there are constants M

such that

kuk

 M

kuk

for all u 2 H

Since H vanishes in a neighborhood of z D 0 and is quadratic at inﬁnity, it

follows that H.z/  cjzj

for all z 2 R

, for a constant c. Therefore, the Sobolev

estimate above leads to the estimate

b.x/ D

H.x.t//dt

 c

jx.t/j

D ckxk

 Kkxk

;

for all x in E, with a constant K>0.Ifx 2 E

, then

ˆ.x/ 

kxk

 Kkxk

Dkxk



 Kkxk



Choosing

˛ ´

;

298 Chapter VII. Symplectic invariants

we obtain the desired estimate

ˆ.x/ 

μ ˇ>0 for all x 2 

The proof of Lemma VII.28 is complete. 

The proof of Lemma VII.29 is of topological nature and based on the Leray–

Schauder degree which we shall brieﬂy recall next. We start by recalling the

Brouwer mapping degree which is probably known to most our readers. It counts the

algebraic number of the solutions of an equation f.x/D y in an open bounded set

  R

where f W

 ! R

is a continuous mapping and where y 2 R

nf.@/.

Thus we consider triples .f;;y/consisting of an open bounded subset   R

a continuous map f W

 ! R

and a point y 2 R

nf.@/. Such a triple is called

admissible.

Proposition VII.31 (Brouwer). There exists a unique map d associating with ev-

ery admissible triple .f;;y/ an integer d.f; ; y/ 2 Z satisfying the following

properties.

(d1) Normalization. d.Id;;y/D 1 for all y 2 .

(d2) Additivity. If 

and 

are two disjoint open subsets of  and if y …

 n 

[ 

/, then d.f; ; y/ D d.f; 

;y/Cd.f; 

;y/.

(d3) Homotopy invariance. If h W

  Œ0; 1 ! R

is a continuous map and

y W Œ0; 1 ! R

a continuous curve satisfying y.t/ … h.@; t / for all t, then

d.h.; t /; ; y.t// is independent of t.

(d4) Existence principle. If d.f; ;y/ ¤ 0, then there exists a solution of f.x/ D

y in .

(d5) Continuity. The map f 7! d.f; ; y/ 2 Z is continuous with respect to

the supremum norm. More explicitly, d.f;;y/ D d.g; ; y/ for all g

satisfying the estimate kf  gk

/

< dist.y; f .@//.

The map d in the proposition is called a Brouwer mapping degree.

Proof. We merely give a rough sketch of the proof. We consider an admissible

triple .;f;y/ and approximate the continuous map f by a smooth map g 2

.; R

/ \ C

; R

/, so that kf  gk

/

<rwhere r ´ dist.y; f .@//

is a positive number, since f.@/ is a compact set. If y is a regular value of the

function g, so that dg.x/ is a linear isomorphism at every preimage x 2 g

1

.y/,

then one deﬁnes the integer

d.f; ; y/ ´

x2f

1

.y/

sign det dg.x/:

By the implicit function theorem the set f

1

.y/ is ﬁnite. If y is not a regular value

one chooses a regular value y

near y in the same component of R

nf.@/making

VII.5. Existence of a critical point of ˆ 299

use of Sard’s theorem. One proves that the integer d.f; ; y/ is independent of the

choice of the smooth function g and the regular value y

near y and satisﬁes the

desired properties. This ﬁnishes the sketch of our proof. 

For detailed proofs we refer to the monographs [26] by K. Deimling, [5]by

H. Amann and [13] by R. Brown. We also recommend the IMPA- lectures [4]by

H. Amann. A classic are the marvelous lectures [67] by J. Milnor. A homological

construction of the Brouwer mapping degree can be found in Appendix 7 in [52]

by H. Hofer and E. Zehnder.

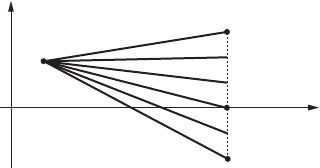
We illustrate the Brouwer degree by a simple example.

Example. We consider the open set  D .a; b/  R whose closure is equal to

 D Œa; b and a smooth function f W Œa; b ! R. We would like to count the

solutions of f.x/ D 0 and hence consider the triples .f;;0/. For such triples to

be admissible, we have to require that 0 … f.@/, so that f.a/ ¤ 0 ¤ f.b/.In

addition, we assume that y D 0 is a regular value of f , so that

d.f; ; 0/ D

x2f

1

.0/

sign f

.x/:

In order to compute the index we deform the function f to the afﬁne linear function

W Œa; b ! R, determined by f

.a/ D f.a/ and f

.b/ D f.b/, by means of

the admissible homotopy h.x; t / D tf

.x/ C .1  t/f.x/ for t in Œ0; 1 which is

illustrated in Figure VII.14. Using the homotopy invariance of degree 1 obtains

d.f; ; 0/ D d.f

;;0/D

1; f.a/>0>f.b/;

C1; f.a/<0<f.b/;

0; f .a/  f.b/>0:

h.x; t/

C1C1 11

Figure VII.14. Using the homotopy invariance for the calculation of d .

We point out that the index can change during a non-admissible homotopy

as the following example illustrates. We choose the functions f

and f

as il-

lustrated in Figure VII.15 and deﬁne the homotopy between them by h.x; t / D

300 Chapter VII. Symplectic invariants

.x/C.1t/f

.x/. Since there exists a parameter value t

satisfying h.t

;b/ D 0,

the homotopy is not admissible and the invariance of the degree is lost, since

d.f

;;0/D 0 and d.f

;;0/D1.

h.x; t/

.b/

h.b; t

Figure VII.15. An example of a non-admissible homotopy.

In order to deﬁne the mapping degree in an inﬁnite dimensional normed real

vector space F , the class of maps under consideration has to be restricted. We

consider triples .f;;y/where   F is an open and bounded subset, f W

 ! F

a continuous map, such that, in addition, the map f  Id is a compact map, hence

mapping bounded sets onto relatively compact sets. Moreover, y 2 F satisﬁes

y … f.@/. These maps f are sometimes called compact vector ﬁelds and we

abbreviate the set of compact vector ﬁelds f W

 ! F by KV.

; F /.

Remark. If  is bounded and if f W

 ! F is a compact vector ﬁeld, then f is a

closed map, that is, if A 

 is a closed set, then its image f .A/ is also a closed

set.

Proof. We assume that A 

 is a closed set and that the sequence f.x

/ of points

in f .A/ converges to a point y in F . Since A is a bounded set and f  Id is

a compact map, the image set .f  Id/.A/ is relatively compact. Therefore, the

sequence f.x

/ x

possesses a convergent subsequence and hence the sequence

has a convergent subsequence x

which necessarily converges to an element

x in A, because A is a closed set. The continuity of the map f implies that

y D lim f.x

/ D f.x/ 2 f .A/ which proves the remark. 

Theorem VII.32 (Leray–Schauder). There exists a unique map D associating with

every admissible triple .f;;y/in which

  F is open and bounded, f 2 KV.

; F / and y 2 F n f.@/

an integer D.f; ; y/ in Z satisfying the following axioms.

(D1) Normalization. D.Id;;y/D 1 for all y 2 .