Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

VII.5. Existence of a critical point of ˆ 301

(D2) Additivity. If 

and 

are two disjoint open subsets of  and if y …

 n 

[ 

/, then D.f; ; y/ D D.f; 

;y/CD.f; 

;y/.

(D3) Homotopy invariance. If h W

  Œ0; 1 ! F is a continuous map such that

the map .x; t/ 7! h.x; t/x is compact and if y W Œ0; 1 ! F is a continuous

curve satisfying y.t/ … h.@; t/ for all t , then the integer D.h.; t/; ; y.t//

is independent of t .

This map D is called the Leray–Schauder degree.

Postponing the proof of this theorem, we shall ﬁrst derive some consequences

of the axioms.

Proposition VII.33. The axioms (D1)–(D3) of the Leray–Schauder degree imply

the following additional properties:

(D1

) D.Id;;y/ D 1 for y 2  while D.Id;;y/ D 0 for y …

.

(D4) D.f; ;;y/ D 0 for all y 2 F .

(D5) Excision property. For an open set 

  satisfying y … f.

 n 

/ we

have D.f; ; y/ D D.f; 

;y/.

(D6) Existence principle. If D.f; ; y/ ¤ 0, then y 2 f ./, i.e., there exists a

solution of f.x/ D y in .

(D7) Continuity. The map f 7! D.f; ; y/ 2 Z is continuous with respect

to the supremum norm. More explicitly, D.f; ; y/ D D.g; ; y/ for all

g 2 KV.

; F / satisfying the estimate kf  gk

/

< dist.y; f .@//.

(D8) Translation invariance. D.f; ; y/ D D.f  y; ; 0/ for all y 2 F .

(D9) Boundary value property. If f; g 2 KV.

; F / satisfy f j

@

D gj

@

, then

D.f; ; y/ D D.g; ; y/.

Proof. The property (D1

) follows from the axioms (D2) and (D1) by choosing



D  and 

a small ball around y satisfying 

\ 

D;. From the axiom

(D2) we conclude the property (D4) by choosing 

D  and 

D;.As

a consequence, the property (D5) now follows from axiom (D2) and from (D4)

by choosing 

D;. Property (D9) is deduced from axiom (D3) by using the

homotopy h.x; t/ D tf .x/ C .1  t/g.x/, and property (D8) follows from axiom

(D3) choosing the homotopy h.x; t/ D f.x/ty and the continuous curve y.t/ D

.1  t/y.

In order to prove property (D6) indirectly we assume that D.f; ; y/ ¤ 0

and y … f ./. Then y … f.

/, since by assumption y … f.@/. Choosing



D 

D;in axiom (D2) we conclude by property (D4) that D.f; ; y/ D 0

contradicting our assumption.

Finally, in order to verify property (D7) we recall that f is a closed map, so

that r D dist.y; f .@// is positive, if y … f.@/.Ifg 2 KV.

; F / satisﬁes

kf  gk

.;F /

<r, then the homotopy h.x; t/ D f.x/ C t.g.x/  f.x// is

admissible and hence, by axiom (D3), D.f; ; y/ D D.g; ; y/. Thus the map

302 Chapter VII. Symplectic invariants

D.;;y/ is locally constant in f and hence continuous in the supremum norm.

This completes the proof of Proposition VII.33. 

The proof of Theorem VII.32 follows from the properties of the Brouwer map-

ping degree together with the following two technical lemmata.

Lemma VII.34. If B  F is a closed and bounded subset of the normed space F ,

then a continuous and compact mapping g W B ! F can be approximated in the

supremum norm by continuous compact maps whose images are contained in ﬁnite

dimensional subspaces of F .

Proof. Let ">0. Since

g.B/iscompact, there exist ﬁnitely many points y

;:::;y

in the image g.B/ such that

g.B/ 

[

iD1

Introducing the continuous functions '

.y/ ´ maxf0; " ky  y

kg for y 2

g.B/ we observe that the functions

.y/ D '

.y/=

j D1

.y/ are well deﬁned

continuous functions on

g.B/ and we deﬁne the map g

on B into F by

.x/ ´

iD1

.g.x//y

;x2 B:

The map g

is continuous and compact and its image g

.B/ is contained in the ﬁnite

dimensional subspace spanfy

;:::;y

gof F . Further, in view of

iD1

.y/ D1

for y in

g.B/,

sup

x2B

kg.x/  g

.x/k";

as is readily veriﬁed. 

Lemma VII.35. Let   F

D R

be an open and bounded subset, and let

f W

  F

! F

be a continuous map satisfying

.f  Id/.

/  F

;

where F

 F

is a linear subspace of F

.Ify 2 F

n f.@/, then the Brouwer

degree satisﬁes

d.f; ; y/ D d.f j

\F

;\ F

;y/:

Proof. If m D dim F

we can assume without loss of generality that the subspace

is represented as

Dfx 2 F

j x

mC1

DDx

D 0g:

VII.5. Existence of a critical point of ˆ 303

In view of the construction of the Brouwer degree we may assume that the map

f is smooth and that y is a regular value of f . The map g ´ f  Id has the

representation g.x/ D .g

.x/;:::;g

.x/;0;:::;0/. Thus

df .x/ D dg.x/ C 1



d.gj

/.x/ 

0 0



C 1



d.f j

/.x/ 

0 1

nm



We read off that det df .x/ D det d.f j

/.x/ and the claim is proved. 

Proof of Theorem VII.32. Again we merely sketch the construction of the Leray–

Schauder degree. Considering admissible triples .f;;y/ we ﬁrst observe that

it sufﬁces to consider the special case y D 0. Indeed, if we have deﬁned the

degree D.f; ; y/ satisfying the axioms (D1)–(D3) of the theorem and then use

the translation invariance of KV.

; F /, we obtain the general case by setting

D.f; ; y/ ´ D.f y; ; 0/. By assumption, the map g D f Id W   F ! F

is continuous and compact and by Lemma VII.34 there exists a continuous and

compact map g

close to the map g in the supremum norm whose image lies in a

ﬁnite dimensional subspace F

 F . Introducing the open set 

´  \ F

we consider the continuous map f

´ g

C Id W



 F

! F

and deﬁne

D.f; ; 0/ D d.f



;

;0/

where d is the Brouwer degree.

If we take another approximation g

of f Id having its image in the ﬁnite di-

mensional subspace F

we can similarly deﬁne the Brouwer degree d.f



;

;0/.

Take now the ﬁnite dimensional subspace F

D spanfF

gand set 

D \F

Then it follows from Lemma VII.35 together with the continuity of the Brouwer

degree that

d.f



;

;0/D d.f



;

;0/D d.f



;

;0/D d.f



;

; 0/;

so that D.f; ; 0/ is well deﬁned. One can demonstrate that the axioms (D1)–(D3)

for D.f; ; 0/ follow from the properties of the Brouwer degree simply by applying

its properties to the ﬁnite dimensional approximations. 

We now use the Leray–Schauder degree in order to prove Lemma VII.29.

Proof of Lemma VII.29 [Degree theory]. We shall prove that '

.†



/ \  ¤;for

all t  0,if is large enough.

304 Chapter VII. Symplectic invariants

(1) By deﬁnition of  we look for a point x 2 † satisfying '

.x/ 2 E

and

.x/kD˛. We abbreviate the ﬂow by 

.x/ D x  t . Then, we have to solve in

view of the orthogonal decomposition E D E



˚ E

, the equation

0 D .P



C P

/.x  t/;

˛ Dkx  tk;

x 2 †:

Using the representation

x  t D e



C x

C e

t

C K.t; x/

of the ﬂow from Proposition VII.26, this is equivalent to solving the equation

0 D e



C x

C .P



C P

/K.t; x/;

0 D ˛ kx  tk;

x 2 †:

Since an element x of † is by deﬁnition of the form x D x



Cse

where

0  s  , we can rewrite the previous equation as an equation of the form

0 D x C B.t; x/ for x 2 †

in the normed space F ´ E



˚ E

˚ Re

, where the map B W R  F ! F is

deﬁned by

B.t; x/ D .e

t



C P

/K.t; x/ C P

Œ.kx  t k˛/e

 x:

In view of Proposition VII.26, the map B W R F ! F is continuous and compact.

We are faced with the following situation. For every ﬁxed t  0 we consider the

map

W †  F ! F; f

.x/ D x C B.t; x/

and look for a solution x 2 † of the equation

.x/ D 0;

where f

.x/  x D B.t; x/ is a continuous and compact mapping. We know from

Lemma VII.28 and the following discussion that '

.@†/ \ D;for all t  0,so

that there are no solutions x 2 @† of f

.x/ D 0 on the boundary, that is,

0 … f

.@†/ for all t  0:

(2) We can, therefore, apply the Leray–Schauder degree in order to show that

D.f

;

†; 0/ ¤ 0 for all t  0;

VII.5. Existence of a critical point of ˆ 305

where

† denotes the interior of †. Using the homotopy invariance of the degree

we conclude

D.f

;

†; 0/ D D.f

;

†; 0/; t  0:

In view of K.0; x/ D 0, the map f

W † ! F has the representation

.x/ D x C P

Œ.kxk˛/e

 x; x 2 †:

We now deform the map f

using the homotopy



.x/ D x C P

Œ.kxk˛/e

 x; x 2 †

where  2 Œ0; 1, so that

.x/ D f

.x/;

.x/ D x  ˛e

if  D 1 resp.  D 0.

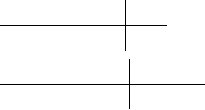
Claim. We claim that if  is sufﬁciently large, then g



.x/ ¤ 0 for all x 2 @† and

the homotopy is admissible.



˚ E

†

˛e

e

Figure VII.16. Illustrating the proof of Lemma VII.29.

Proof of the claim. If g



.x/ D 0 for a point x 2 †, then, necessarily, x D se

for

some s  0 and inserting x D se

into the equation

0 D g



.x/ D x C P

Œ.kxk˛/e

 x

we see that s solves the equation

sŒ.1  / C ke

k D ˛:

306 Chapter VII. Symplectic invariants

Recalling ke

2 > 1 and 0    1 it follows that

0<s ˛:

If x D se

2 @†, then s D 0 or s D . Thus, there exists no solution of



.x// D 0 on the boundary @†,if>˛. Finally, also the compactness condition

for the homotopy is satisﬁed, since the image of the map g



Id lies in the subspace

of dimension 1 and we have veriﬁed that the homotopy is indeed admissible,

as claimed. 

Consequently, using the homotopy invariance and the translation invariance of

the Leray–Schauder degree we obtain

D.f

;

†; 0/ D D.g

;

†; 0/

D D.g

;

†; 0/

D D.Id ˛e

;

†; 0/

D D.Id;

†; ˛e

From Proposition VII.33 we know that D.Id;

†; ˛e

/ D 1,if˛e

†. Since the

latter is equivalent to >˛, we have proved that

D.f

;

†; 0/ D 1 for all t  0;

if  is sufﬁciently large. In view of the existence principle in Proposition VII.33

there exists for every t  0 a point x in the interior of † which solves the equation

.x/ D 0. Therefore, '

.†/ \ ¤;for all t  0 and the proof of Lemma VII.29

is complete. 

With Lemma VII.29 the proofs of Theorem VII.27 and hence that of Theo-

rem VII.15 are complete and we have ﬁnally established the existence of the Hofer–

Zehnder symplectic capacity function c

. It does not only explain the rigidity

phenomena in symplectic geometry described above, but also helps to ﬁnd global

periodic solutions of Hamiltonian vector ﬁelds on compact energy surfaces, as the

next chapter will demonstrate.

Literature. Chapter VII is based on part of the book [52] by H. Hofer and E. Zehn-

der which contains many references and remarks about the history of the results. An

introduction to symplectic topology is the book [65] by D. McDuff and D. Salamon.

As for embedding problems in symplectic geometry we refer to the monograph [99]

by F. Schlenk. For recent developments and applications of symplectic capacities

as well as for all the references and many open problems we recommend [18]by

K. Cieliebak, H. Hofer, J. Latschev and F. Schlenk.

Chapter VIII

Applications of the capacity c

in Hamiltonian

systems

In Chapter VIII we use the dynamical capacity c

to tackle the problem of ﬁnding

periodic orbits of a Hamiltonian vector ﬁeld on a prescribed compact energy surface

S. We shall establish an abundance of periodic orbits in an open neighborhood U

of S if only the Hofer–Zehnder capacity c

.U; !/ is ﬁnite. However, in order

to guarantee periodic orbits on S itself, the class of energy surfaces has to be

restricted, for example to the class of contact type hypersurfaces introduced by A.

Weinstein. We shall recover, in particular, the pioneering results of A. Weinstein

and P. Rabinowitz for convex and starlike hypersurfaces. It turns out that compact

energy surfaces of classical mechanical systems of the form kinetic energy plus

potential energy always carry a periodic orbit. A classical result due to H. Poincaré

shows that, in general, a periodic solution belongs to a smooth family of periodic

solutions parametrized by the energy and having similar periods.

VIII.1 Global periodic solutions on prescribed energy

surfaces

The ﬂow '

of a Hamiltonian vector ﬁeld X

on a symplectic manifold .M; !/

leaves the level sets of the smooth Hamiltonian function H on M invariant because

H.'

.x// D H.x/ as long as the ﬂow is deﬁned. Fixing a value of the energy

function H which we may assume without loss of generality to be E D 0, we shall

require that the energy surface

S Dfx 2 M j H.x/ D 0g

is compact and regular requiring that dH.x/ ¤ 0 on S. Thus S  M is a smooth

and compact submanifold of codimension 1 (a compact hypersurface) whose tangent

space at the point x 2 S is given by T

S D ker dH.x/. By deﬁnition of a

Hamiltonian vector ﬁeld we have X

.x/ 2 T

S so that X

is a nowhere vanishing

vector ﬁeld on the energy surface S whose ﬂow does exist for all times, since S is

compact. Our aim is to ﬁnd periodic solutions of X

on the energy surface S.

It is useful to recall from Section VI.3 that the orbits of X

on S only depend on

the hypersurface and the symplectic form ! and not on the choice of the function

H which represents S as a regular energy surface. Indeed, if H and F are two

Hamiltonian functions representing S as

S DfH D c

gDfF D c

g;dH.x/¤ 0; dF .x/ ¤ 0; x 2 S;

308 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

then the tangent space T

S D ker dH.x/ D ker dF .x/  T

M is of codimension 1

and hence there exists a real number .x/ ¤ 0 satisfying dF .x/ D .x/dH.x/ for

x 2 S. Consequently,

.x/ D .x/X

.x/; x 2 S;

for a smooth nowhere vanishing function  W S ! R. Of course, this only holds

true on the given hypersurface S . The ﬂows '

of X

and

of X

on S are

related by

psi

s.t;x/

.x/ D '

.x/; x 2 S;

where the function s W R  S ! R satisﬁes

s.t;x/ D

d

.'



.x//

; s.0; x/ D 0;

as has already been mentioned in Chapter VI. We see that the orbits of the Hamilto-

nian vector ﬁelds X

and X

are indeed the same, only their parametrizations are

different. To formulate this fact geometrically we have introduced the canonical

line bundle L

of S whose ﬁbre over the point x is the line

.x/ D ker.!j

/ Dfu 2 T

S j !.u; v/ D 0 for all v 2 T

in the tangent space T

S. This line determines the direction of every Hamiltonian

vector ﬁeld whose Hamiltonian function has S as a regular energy surface. Con-

sequently, instead of looking for periodic solutions of X

on the hypersurface S

we can just as well look for closed characteristics of the canonical line bundle L

They agree with the set of unparametrized periodic solutions of every Hamiltonian

vector ﬁeld X

on S having S as a regular energy surface.

Our trick in the search for periodic solutions on S is to thicken the given energy

surface S Dfx 2 M j H.x/ D 0g and to consider a one-parameter family

of energy surfaces nearby. Since S is compact and regular there is an open and

bounded neighborhood U of S which is ﬁlled with compact and regular energy

surfaces having energy values near E D 0,

U ´

[

2I



where I D ."; "/ is an open interval around  D 0 and where



Dfx 2 U j H.x/ D g;2 I

is diffeomorphic to the given surface S D S

which corresponds to the parameter

value  D 0. Indeed, the following proposition holds true.

VIII.1. Global periodic solutions on prescribed energy surfaces 309



Figure VIII.1. Thickening of the compact energy surface S and the neighborhood U .

Proposition VIII.1. If I D ."; "/ is an open interval and ">0sufﬁciently small,

then

U ´

[

2I



is the image of a diffeomorphism W S  I ! U satisfying .S fg/ D S



where S



Dfx 2 U j H.x/ D g.

Proof. We choose a Riemannian metric h; i on the manifold M and deﬁne the

gradient rH.x/ of the function H at the point x 2 M as usual by

dH.x/v DhrH.x/; vi;v2 T

The smooth gradient vector ﬁeld rH on M does not vanish at any point in U so

that

dH.x/ rH.x/ DhrH.x/;rH.x/iDjrH.x/j

>0:

The vector rH.x/ is orthogonal to the tangent space T

S, since

hrH.x/;viDdH.x/v D 0 for all v 2 T

S D ker dH.x/:

Therefore the ﬂow

of the modiﬁed gradient equation

Px D

rH.x/

jrH.x/j

;x2 M near S

is transversal to the energy surface S and we claim that

.x// D t; x 2 S; jt j <"

for ">0small, as long as the gradient does not vanish. Indeed,

.x// D dH.

.x//

.x/



rH.

.x//;

rH.

.x//

jrH.

.x//j



D 1;

310 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

and hence

.x// D H.

.x// C

.x// ds D H.x/ C t:

If x 2 S , then H.x/ D 0 so that the claim is proved. The ﬂow

deﬁnes a

diffeomorphism W S  I ! U given by .x; t/ 7!

.x/ where I D ."; "/

is an open interval and ">0sufﬁciently small. The diffeomorphism satisﬁes

.S/ D S

, and .0; / is the identity map on S. The proof of Proposition VIII.1

is complete. 

If the capacity c

of an open and bounded neighborhood U of S is ﬁnite, the

following statement guarantees plenty of periodic solutions near S.

Theorem VIII.2 (Hofer–Zehnder). Let S Dfx 2 M j H.x/ D 0g be a compact

and regular energy surface of the Hamiltonian vector ﬁeld X

in the symplectic

manifold .M; !/ and let

U ´

[

2I



be the bounded open neighborhood of S from the previous proposition where I D

."; "/ is an open interval. If

.U; !/ < 1;

then there exists a dense subset ƒ  I in the parameter interval such that for every

parameter  2 ƒ the associated energy surface S



carries a periodic solution

of X

It should be emphasized that there are no assumptions required for the given

compact and regular energy surface S other than that the bounded open neighbor-

hood must have ﬁnite capacity c

. In the special case in which the symplectic

manifold is the standard space .R

/, the assumption c

.U; !/ < 1 is always

satisﬁed, because the relatively compact neighborhood U is contained in a large

ball B.R/ of capacity c

.B.R// D R

< 1 and because the capacity function

possesses the monotonicity property. Therefore, every compact regular energy sur-

face S  R

gives rise to an abundance of periodic solutions of the Hamiltonian

vector ﬁeld whose energies are near the prescribed energy of S.

Proof [Deﬁnition of c

]. The statement is an immediate consequence of the deﬁ-

nition of the capacity c

.If

2 I and ">0are given, we want to show that there

exists a parameter  2 I satisfying j

 j <", for which S



carries a periodic

solution. We can assume without loss of generality that 

D 0. In order to deﬁne

a special Hamiltonian function F 2 H.U; !/ that is constant on every surface S

