Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

VII.3. Minimax principles 271

and kI.e



/kDke





holds true. Therefore, there exists for every x 2 E a unique

v.x/ 2 E satisfying

df .x/y Dhv.x/;yi for all y 2 E

and kdf .x/k



Dkv.x/k, namely v.x/ D I.df .x//. The point v.x/ 2 E is called

the gradient of the function f at the point x with respect to the scalar product h; i

and denoted by v.x/ Drf.x/, so that

df .x/y Dhrf.x/;yi for all y 2 E:

The critical points of the function f are the zeroes of the gradient vector ﬁeld

x 7!rf.x/

on E and we can interpret the critical points of f dynamically as equilibrium points

of the gradient equation

Px Drf.x/; x 2 E

which is an ordinary differential equation in the Hilbert space E.

In the following we assume that the gradient equation generates a unique global

ﬂow '

satisfying

.x/ Drf.'

.x//; t 2 R;

.x/ D x; x 2 E;

by requiring that the initial value problem can be uniquely solved for all times and

for all initial conditions x 2 E. Such a global ﬂow does exist, for example, if the

gradient of the function f satisﬁes a global Lipschitz estimate krf.x/rf.y/k

M kx  yk for a constant M and all x; y 2 E, as we have seen in Chapter IV.

From Chapter IV we recall the crucial property of the gradient ﬂow. The function

t 7! f.'

.x// decreases along non-constant solutions, in view of

f.'

.x// D

krf.'

.x//k

, from which one obtains by integration the identity

f.'

.x// D f.x/

krf.'

.x//k

ds:

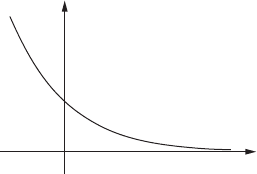
A differentiable function f W E ! R does not need to have critical points,

even if it is bounded below, because the space E is non-compact. The function

f.x/ D e

x

on R satisﬁes krf.x

/k!0 for every sequence x

!1, and

the sequence f.x

/ is bounded, however the sequence does not have a convergent

subsequence.

We introduce the so-called P.S.-condition, which goes back to R. S. Palais and

S. Smale. It is one of the classical compactness conditions of nonlinear functional

analysis which, in many cases, guarantees critical points.

272 Chapter VII. Symplectic invariants

Deﬁnition. A function f 2 C

.E; R/ satisﬁes the P.S.-condition, if every sequence

2 E satisfying

rf.x

/ ! 0 in E and jf.x

/jc for all j

possesses a convergent subsequence where c is a constant.

Then, the limit x



of such a subsequence is necessarily a critical point of f ,

rf.x



/ D 0;

because the function f is of class C

Deﬁnition. Let F be a family of subsets F  E and f 2 C

.E; R/. The minimax

c.f;F/ of the pair .f; F/ is deﬁned as

c.f;F/ ´ inf

F 2F



sup

x2F

f.x/



2 R [ f˙1g:

We shall apply the strategy of the following proposition later on in order to

guarantee a critical point of the action functional.

PropositionVII.17 (Minimax principle). We require that the function f 2C

.E; R/

and the family F meet the following conditions.

(i) f satisﬁes the P.S.-condition.

(ii) Px Drf.x/deﬁnes a unique global ﬂow '

.x/ on the Hilbert space E.

(iii) The family F is positively invariant under the ﬂow, i.e., for all t  0 we

conclude from F 2 F H) '

.F / 2 F:

(iv) The minimax is ﬁnite, 1 < c.f; F/<1.

Then the real number c.f; F/ is a critical value of f , i.e., there exists a point x



2 E

satisfying

rf.x



/ D 0 and f.x



/ D c.f; F/:

f.x/ D e

x

Figure VII.9. The function f.x/ D e

x

on E D R does not have a critical point, even

though rf.x/ ! 0 for x !1.

VII.3. Minimax principles 273

Proof. We abbreviate the minimax by c ´ c.f; F/. It sufﬁces to prove the follow-

ing claim.

Claim. For every ">0there exists a point x 2 E satisfying

c  "  f.x/  c C " and krf.x/k":

Indeed, if this holds true, the proposition follows, since taking the sequence

! 0 we obtain a sequence x

2 E satisfying

c 

 f.x

/  c C

and krf.x

/k

Because f satisﬁes the P.S.-condition, there exists a convergent subsequence of x

Its limit x



satisﬁes rf.x



/ D 0 and f.x



/ D c.f;F/, because the functions f

and rf are continuous.

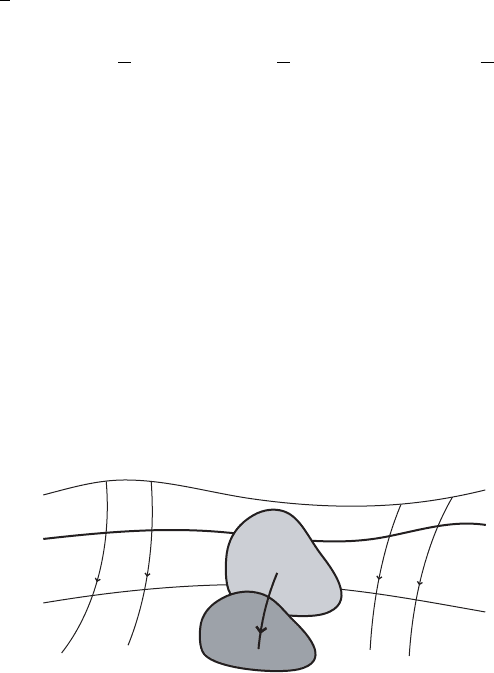
Proof of the claim. In order to prove the claim, we proceed by contradiction and

assume that there exists an ">0satisfying

krf.x/k >" for all x 2fx j c  "  f.x/  c C "g:

Using the deﬁnition of c we ﬁnd a set F 2 F satisfying sup

x2F

f.x/  c C ".

If x 2 F , then f.x/  c C " and we shall show that

./f.'



.x//  c  " for t



D 2"

1

c C "

c  "



Figure VII.10. The proof of the minimax principle by contradiction.

This produces the desired contradiction, since for the set F



D '



.F / 2 F it

follows that

sup

x2F



f.x/  c  ";

274 Chapter VII. Symplectic invariants

which is in contradiction to the deﬁnition of the minimax c. It remains to prove the

estimate ./.Iff.'

.x//  c " for some time t in the interval 0  t  t



, then,

indeed, f.'



.x//  c  ", because f.'

.x// is decreasing if t increases. If, on

the other hand

./f.'

.x// > c  " for all 0  t  t



;

then it follows from our assumption that krf.'

.x//k >"for all 0  t  t



Using the identity f.'

.x// D f.x/

krf.'

.x//k

ds we obtain the estimate

f.'



.x//  c C "  "



D c  ";

in contradiction to the estimate ./. Thus, the estimate ./ holds true and the

minimax principle is proved. 

Example. We assume that the function f on E satisﬁes the P.S.-condition and that

the corresponding gradient equation generates a unique global ﬂow, as speciﬁed

in the assumptions (i) and (ii) of the proposition. In addition, we require that the

function f is bounded below, so that 1 <˛ f.x/for all x 2 E. As a minimax

family F of sets we choose the family of all points, namely F Dfxg

x2E

. Then

˛  c.f; F/ ´ inf

x2E

f.x/ < 1

and therefore c.f; F/ 2 R. Since there is nothing to prove for (iii), we conclude

from the minimax principle the existence of a point x



2 E satisfying

f.x



/ D inf

f and rf.x



/ D 0:

We have proved that a global minimum of the function f exists!

As a further illustration we formulate the mountain pass lemma.

Deﬁnition. A subset R  E is called a mountain range for the function f ,

(i) if the restriction f j

is bounded below, so that inf

x2R

f.x/ μ ˛>1,

(ii) if the set E n R has at least two connected components and if in every com-

ponent there exists a point x satisfying f.x/<˛.

PropositionVII.18 (Mountain pass lemma). We assume that a function f W E ! R

is continuously differentiable and satisﬁes the P.S.-condition and that, moreover,

Px Drf.x/ generates a unique global ﬂow. If R  E is a mountain range for

f , then f has a critical value c 2 R satisfying

c  inf

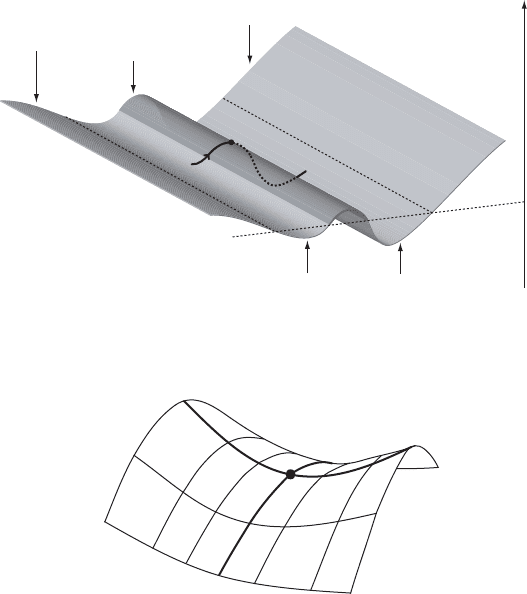
VII.3. Minimax principles 275

f.x/

Figure VII.11. A mountain range R and the connected components E

of E n R.

Figure VII.12. Saddle point on a path  2  over the mountain range.

Proof [Minimax principle]. If we choose two different connected components E

and E

of E nR according to the deﬁnition (ii) of a mountain range and if we deﬁne

for j D 0; 1 and ˛ D inf

x2R

f.x/the sublevel sets

Dfx 2 E

j f.x/<˛g;

then E

¤;. Next, we consider the set  of paths connecting the two valleys,

deﬁned by

 Df W Œ0; 1 ! E continuous j .0/ 2 E

and .1/ 2 E

and deﬁne the family F of subsets of E as

F Df.Œ0; 1/ j  2 g:

276 Chapter VII. Symplectic invariants

The sets .Œ0; 1/ are compact, because the curves are continuous. Since .0/

and .1/ belong to different components of E n R, there exists a parameter value

2 .0; 1/ satisfying .t

/ 2 R, so that

f..t

//  ˛:

Therefore, ˛  sup

x2.Œ0;1/

f.x/ < 1 for all paths  2 , so that

1 <˛ c.f;F/ D inf

2

sup

x2.Œ0;1/

f.x/ < 1:

Consequently, the minimax is ﬁnite. It remains to prove that F is positively invariant

under the ﬂow '

of the vector ﬁeld rf . Due to the monotonicity,

f.'

.x//  f.'

.x// D f.x/; x 2 E; t  0:

Hence, in view of the deﬁnition of R, the ﬂow cannot leave the sublevel sets of the

components E nR so that '

B 2  for  2  and t  0. Now, we can apply the

minimax principle from which the proposition follows. 

Our next task is to extend our action functional ˆ to a continuously differentiable

function deﬁned on a suitable Hilbert space E which contains the set C

; R/ of

smooth loops as a linear subspace. Moreover, we have to look for a suitable family

F, so that we can perform the minimax strategy.

VII.4 The functional analysis of the action functional

We return to the action functional ˆ W  D C

; R

/ ! R, deﬁned by

ˆ.x/ ´

hJ Px.t/; x.t/iH.x.t//dt;

where the smooth function H W R

! R has the properties

(i) H  0 near z D 0 and

(ii) H.z/ D Q.z/ for jzj large.

The quadratic form Q is deﬁned by

Q.z/ D . C "/ q.z/

for a small ">0. We shall extend the function ˆ onto a Hilbert space E   and

shall translate the pointwise properties (i) and (ii) of H into the qualitative behavior

of the extended function ˆW E ! R. In order to ﬁnd a suitable Hilbert space E,

we consider the dominant part of ˆ, namely

a.x; y/ ´

hJ Px.t/; y.t/idt:

VII.4. The functional analysis of the action functional 277

We represent the loops x; y 2 C

; R

/ by their Fourier series

x.t/ D

j 2Z

j2tJ

2 R

Since x belongs to C

/, its Fourier series does converge not only in L

,but

also in the supremum norm and even in every C

-norm. Inserting the Fourier series

of the loops x.t/ and y.t/ into a.x; y/, recalling that J

D1 and observing that

j2tJ

k2tJ

idt D ı

i, one obtains

2a.x; y/ D 2

j 2Z

j hx

D 2

j>0

jj jhx

i2

j<0

jj jhx

This representation shows that a.x; y/ can be extended to the Sobolev space

; R

/ as a continuous bilinear form.

Deﬁnition. The Sobolev space H

D H

; R

/ for a real number s  0 is

deﬁned as

x 2 L

; R

/ j

j 2Znf0g

jj j

< 1



;

where x

2 R

denote the coefﬁcientsof the Fourier series x.t/ D

j 2Z

j2tJ

which converges in L

. The space H

is a Hilbert space equipped with the scalar

product

hx; yi

´hx

iC2

j 2Znf0g

jj j

and the norm kxk

Dhx; xi

The norm kk

for s D 0 is equivalent to the L

norm, since, according

to the theorem of Plancherel, kxk

jx.t/j

dt D

j 2Z

and hence

kk

kk



2 kk

. In the following the Sobolev space H

will be the

desired Hilbert space E we shall work on and so we introduce the abbreviations

E ´ H

; R

hx; yi´hx;yi

;

kxk

´hx; xi

There exists an orthogonal splitting of E,

E D E



˚ E

;

278 Chapter VII. Symplectic invariants

into the closed subspaces consisting of the elements x 2 E which have non-

vanishing Fourier coefﬁcients only for j<0, j D 0 or j>0. The corresponding

orthogonal projectors are denoted by P

, P

and P



. Therefore, every x 2 E

has the unique decomposition

x D x



C x

2 E



˚ E

where x

D P

x, x

D P

x and x



D P



Deﬁnition. For x; y 2 E we deﬁne the continuous bilinear form a by

a.x; y/ D

i



h.P

 P



/x; yi:

The bilinear form a is an extension of the original bilinear form a deﬁned on

the subspace  of smooth loops. Indeed, for two smooth loops x; y 2   E we

have the representation

a.x; y/ D

hJ Px; yidt:

Deﬁnition. The corresponding quadratic form a W E ! R is deﬁned by

a.x/ D a.x; x/ D





;xD x

C x



The function a W E ! R is continuously differentiable and its derivative da.x/

in the point x 2 E is equal to

da.x/.y/ Dhx

ihx



Dh.P

 P



/x; yi:

By deﬁnition of the gradient, da.x/.y/ Dhra.x/; yi for all y 2 E, so that the

gradient of the function a is equal to

ra.x/ D .P

 P



/x D x

 x



2 E:

The map x 7!ra.x/ on E is linear and continuous.

Next, we shall prove some useful properties of the spaces H

. First we note

that these spaces decrease according to

 H

for t  s  0;

while the norms increase,

kxk

kxk

; if x 2 H

VII.4. The functional analysis of the action functional 279

From these estimates one reads off that the inclusion map

I W H

! H

;t s

is a bounded linear operator and therefore also continuous.

Remark. The loop space  D C

; R

/ is contained in the Sobolev space

and is dense, for every s  0.

Proof. The Fourier coefﬁcients x

2 R

of a smooth loop x 2  satisfy the

following estimates. For every integer k  0 there exists a constant c

such that

jc

jj j

for all j 2 Z:

Hence kxk

< 1 for every s. Since already the subset of  consisting of trigono-

metric polynomials x.t/ D

j DN

j2tJ

with N 2 N and x

2 R

is dense

in H

for s  0, the claim follows. 

Deﬁnition. A map between metric spaces is called compact, if it maps bounded sets

onto relatively compact sets, i.e., onto sets whose closure is compact. Equivalently,

the image of a bounded sequence possesses a convergent subsequence.

Since compact sets are bounded, the compact maps map bounded sets onto

bounded sets. In particular, compact linear maps between normed spaces are con-

tinuous maps.

Proposition VII.19. If t>s 0, the inclusion map I W H

! H

is compact.

Proof. If we deﬁne the map P

W H

! H

for the integer N 2 N by

x/.t/ ´

jj jN

j2tJ

for x.t/ D

j 2Z

j2tJ

;

then P

2 L.H

/ is a linear and bounded map. The image under the map P

is a ﬁnite dimensional space in which relatively compact sets and bounded sets are

the same. Therefore P

is a compact map. The set of compact linear operators is

closed with respect to the operator norm, as can be veriﬁed easily. The proposition

therefore follows if we show that

! I in L.H

/; N !1:

280 Chapter VII. Symplectic invariants

For this purpose we compute

k.P

 I/xk



jj j>N

j2tJ



D 2

jj j>N

jj j

D 2

jj j>N

jj j

2.st/

jj j

 N

2.st/

2

jj j>N

jj j

 N

2.st/

kxk

Because t>s,

 I k

L.H

 N

.st/

! 0

as N !1and the proposition is proved. 

Not all the elements of the space E D H

can be represented by continuous

functions. Yet for s>

the Sobolev space H

 C.S

; R

/ is continuously

embedded in the space of continuous functions equipped with the supremum norm.

Proposition VII.20. If s>

, then

x 2 H

H) x 2 C.S

; R

that is, there exists a continuous representative of x 2 H

 L

. Moreover, there

exists a constant c>0such that

sup

t2S

jx.t/jckxk

for all x 2 H

Proof. We shall show that the Fourier series

x.t/ D

j 2Z

j2tJ

of x 2 H

does not only converge in L

, but also in the supremum norm, so that

the limit function is, indeed, a continuous function. For s>

we compute, using