Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

VI.1. Geometric questions 241

We can ask the same question for symplectic instead of volume preserving

diffeomorphisms in the symplectic standard space .R

/.Ifn D 1 we do not

obtain anything new since here the concepts symplectic and area preserving are the

same. Therefore, we assume n  2 and consider two compact domains K

and

of R

which possess smooth boundaries and are diffeomorphic. Under which

conditions on K

and K

can we obtain a diffeomorphism W K

! K

satisfying



D !

;

or explicitly, solving the nonlinear partial differential equation

d .x/

Jd .x/ D J

for x 2 K

? From det d .x/ D 1 we conclude that vol.K

/ D vol.K

/ is again a

necessary condition. Is it also sufﬁcient?

Turning to a seemingly simpler problem we take two open sets U; V  R

and

look for conditions under which there exists a symplectic embedding ' W U ! V

that is a diffeomorphism ' W U ! '.U/  V satisfying '



D !

on U . Clearly,

vol.U / D vol.'.U //  vol.V /

is a necessary condition. Are there other obstructions than the volume?

Let us ﬁrst look at some examples and take the Euclidian open ball

B.R/ Df.x; y/ 2 R

 R

jjxj

Cjyj

gR

of radius R centered at the origin. Is it possible to embed this open ball symplecti-

cally into the isotropic cylinder

iso

.r/ Df.x; y/ 2 R

 R

j x

C x

gR

of a small radius r>0?

We point out that the coordinates refer to the symplectic basis

;:::;e

:::;f

which satisﬁes !

/ D ı

, !

/ D 0 and !

/ D 0. The plane

E D spanfe

g on which the cylinder stands satisﬁes !

D 0, so that the

symplectic form !

does not induce a symplectic structure on E.

For this isotropic cylinder the answer to our question is positive. Indeed, we

simply take the linear map

'.x; y/ D ."x; "

1

y/:

Then '.B.R//  Z

iso

.r/ for every radius r, if only the parameter ">0is chosen

sufﬁciently small. The map ' is symplectic, since it is of the matrix form



1



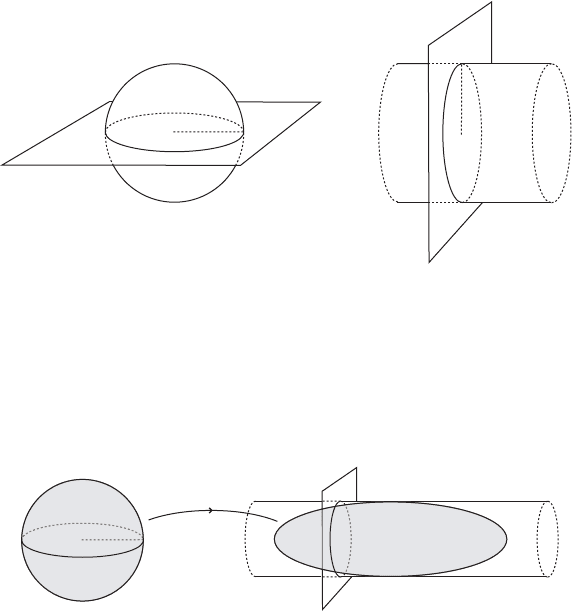
242 Chapter VI. Questions, phenomena, results

B.R/

iso

.r/

E D spanfe

Figure VI.1. The ball B.R/ and the isotropic cylinder Z

iso

.r/.

with respect to the splitting R

R

. We see that we can embed the open ball B.R/

symplectically into the open isotropic cylinder Z

iso

.r/, regardless of the smallness

of r.

B.R/

iso

.r/

E D spanfe

Figure VI.2. Symplectic embedding of a large ball B.R/ into a narrow isotropic cylinder

iso

.r/.

We next take a completely different cylinder, namely the symplectic cylinder

Z.r/ Df.x; y/ 2 R

 R

j x

C y

of radius r>0. This time the cylinder stands on the symplectic plane E D

spanfe

g, where !

/ D 1, so that !

is a symplectic form on E.

Analogous to the above example we are tempted to try with a map of the form

.x; y/ D ."x

1

;:::;x

;"y

1

;:::;y

Choosing " sufﬁciently small, one achieves indeed that .B.R//  Z.r/. The

map is volume preserving, since det d .x; y/ D ""

1

D 1. However,

is symplectic only if " D 1, in which case D Id and hence .B.R//  Z.r/

symplectically only if r  R.

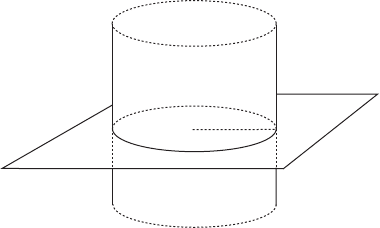
VI.2. Approximation of measure preserving diffeomorphisms 243

Z.r/

E D spanfe

Figure VI.3. The symplectic cylinder Z.r/.

Surprisingly, it is not possible to ﬁnd a symplectic diffeomorphism that does the

job in a more clever way, because M. Gromov discovered in 1985 his seminal non-

squeezing theorem which we shall prove in the next chapter. It says the following:

• If ' W B.R/ ! R

is a symplectic embedding satisfying '.B.R//  Z.r/,

then r  R.

Even though vol.B.R// is ﬁnite, while vol.Z.r// D1, the open ball can only

be embedded symplectically into the symplectic cylinder Z.r/, if the radius of the

cylinder is bigger than or equal to the radius of the ball. This holds true in particular

for every ﬂow map '

of a Hamiltonian differential equation, independent of the

choice of the Hamiltonian function. We see, in particular, that symplectic maps

constitute a much smaller class than volume preserving maps.

From the theorem we draw the conclusion that there must be other symplectic

invariants apart from the volume! Some of them will be constructed in the next

chapter.

VI.2 Approximation of measure preserving diffeomorphisms

Is it possible to approximate measure preserving diffeomorphisms of R

by sym-

plectic maps of .R

/ locally uniformly, that is, in the topology of C

loc

We look at the sequence '

W R

! R

of symplectic maps for j  1, so that

.x/

Jd'

.x/ D J; x 2 R

If the sequence converges to the map ' in the C

loc

-sense, then clearly

d'.x/

Jd'.x/ D J; x 2 R

so that the limit map is again symplectic.

244 Chapter VI. Questions, phenomena, results

If the sequence convergesmerely in the C

loc

-sense to the map ', then the limit ' is

a continuous map which is still measure preserving. Indeed, from det d'

.x/ D 1

for all j we deduce for every smooth function f 2 C

/ having compact

support that

f.'

.x// dx D

f.x/ dx:

Since f.'

.x// ! f.'.x//for every x 2 R

, we obtain in view of the Lebesgue

convergence theorem that

f.'.x//dx D

f.x/ dx:

This holds true for all functions f 2 C

/. Because C

 L

is dense, the

equation holds true for all integrable functions f 2 L

. Therefore, the limit map

' is measure preserving, as claimed.

However, it is a striking phenomenon that the limit map is even symplectic

if it is assumed to be differentiable. Hence the symplectic nature survives under

topological limits in view of the following theorem.

Theorem VI.3 (Eliashberg–Gromov–Ekeland–Hofer). We consider a sequence '

of symplectic mappings in the symplectic standard space, so that '



D !

, which

converges locally uniformly to the map '. If the limit map ' is differentiable in the

point x

, then

d'.x

/ 2 Sp.n/:

Explicitly, d'.x

/ is a linear symplectic map. If, in particular, the limit map is

differentiable, it is necessarily a symplectic map and hence satisﬁes '



D !

It follows that the group of symplectic diffeomorphisms of a compact symplectic

manifold is C

-closed in the group of all diffeomorphisms of the manifold. The

elegant proof by I. Ekeland and H. Hofer is based on the symplectic invariants which

will be introduced in the next chapter and we refer to [52, S. 59].

VI.3 A dynamical question

We recall that the smooth function H W R

! R determines the Hamiltonian vector

ﬁeld X

by the formula !

; / DdH . If the energy surface

S ´fx 2 R

j H.x/ D 0gR

is compact and regular, so that dH.x/ ¤ 0 on S, then X

.x/ ¤ 0 for all x 2 S .

In view of the energy conservation, the Hamiltonian vector ﬁeld is tangent to the

energy surface

.x/ 2 T

S; x 2 S

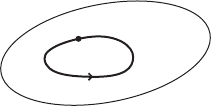
VI.3. A dynamical question 245

and its ﬂow '

leaves the surface invariant,

.S/ D S; t 2 R:

In view of Liouville’s theorem (Proposition V.31) there exists a ﬁnite measure

 on S , which is invariant under the ﬂow maps '

. Therefore, in view of Poincaré’s

recurrence theorem (Theorem I.14) almost every point is recurrent. Consequently,

there exists for almost every point x 2 S a sequence of times t

!1satisfying

lim

j !1

.x/ ! x:

The question arises whether there exists a point x 2 S and a time T>0satisfying

.x/ D x:

From the uniqueness of the solutions it then follows that

tCT

.x/ D '

.x/; t 2 R;

so that '

.x/ is a periodic solution of the vector ﬁeld X

on the energy surface S.

.x/

Figure VI.4. A periodic solution on the energy surface S.

Thickening the regular and compact hypersurface S by considering a whole

family of hypersurfaces



Dfx 2 R

j H.x/ D g;2 I;

parametrized by an open interval I D ."; "/ around 0 for some ">0, we shall

prove in Chapter VIII the following global existence theorem of periodic solutions

on energy surfaces (Theorem VIII.4).

• For almost every  2 I the energy surface S



carries a periodic solution of

the Hamiltonian vector ﬁeld X

We see that a compact regular energy surface S gives rise to an abundance of periodic

solutions of X

in the neighborhood of S ! However, we point out that the given

energy surface S does not necessarily carry a periodic solution, as examples show.

The above existence statement will be deduced from a distinguished symplectic

invariant which also explains the non-squeezing phenomenon of Gromov.

246 Chapter VI. Questions, phenomena, results

S D S



Figure VI.5. Thickening of the energy surface S.

It will be useful for the analysis later on to formulate the existence problem of

periodic orbits on a given hypersurface in more geometrical terms. In order to do

so we shall introduce the canonical line bundle of a hypersurface S  R

. The

hypersurface S is a submanifold of codimension 1, so that the dimension of the

tangent space at x 2 S is equal to dim T

S D 2n  1. Therefore, the restriction

of the symplectic structure !

onto T

S is necessarily degenerate. Because !

nondegenerate on the tangent space T

we conclude

dim



ker.!



D 1; x 2 S

for the kernel of the restriction of the symplectic form !

onto T

S, deﬁned by

ker.!

/ Dfu 2 T

S j !

.u; v/ D 0 for all v 2 T

SgT

This line in the tangent space T

S is denoted by L

.x/ and the canonical line

bundle of the hypersurface S is the subbundle of the tangent bundle TS deﬁned by

´ ker.!

/ ´f.x; u/ 2 TS j !

.u; v/ D 0 for all v 2 T

Sg:

The canonical line bundle of the hypersurface S gives at every point of S the

direction of every Hamiltonian vector ﬁeld X

which has S as its regular energy

.x/

Figure VI.6. Illustration of the line bundle L

VI.4. A connection between geometry and Hamiltonian dynamics 247

surface. Indeed, if

S Dfx 2 R

j H.x/ D cg;dH.x/¤ 0; x 2 S;

it follows for x 2 S that

.x/; v/ DdH.x/v D 0 for every v 2 T

S  ker dH.x/

and therefore X

.x/ 2 ker.!

/ D L

.x/.

As a consequence, the orbits of a Hamiltonian vector ﬁeld X

on a regular

energy surface S  R

depend only on the hypersurface S and on the symplectic

structure !

(except for the parametrization of the individual solutions) and do not

depend on the choice of the Hamilton function H which represents the hypersurface

S as

S Dfx 2 R

j H.x/ D cg;dH.x/¤ 0 if x 2 S

for a constant c.

This observation will allow us later on to choose a Hamiltonian function which

is well suited for the analysis. The orbits of the vector ﬁeld X

on S, that is the

images of the solution curves, lie on the characteristics of the line bundle L

characteristic of L

is a differentiable curve  W I  R ! S satisfying

0 ¤P.t/ 2 L

..t//; t 2 I:

The existence problem of periodic solutions can now be formulated purely geomet-

rically as follows. Does a compact smooth hypersurface S  .R

/ possess a

closed characteristic of the canonical line bundle L

VI.4 A connection between geometry and Hamiltonian

dynamics

If two compact domains with smooth boundaries in the symplectic standard space

are diffeomorphic by a symplectic diffeomorphism of R

, then the canonical line

bundles of their boundaries are isomorphic. Hence the actions of possible closed

characteristics on the boundaries are numerical invariants, as we shall brieﬂy explain

next. In order to deﬁne the action of a closed curve in R

we introduce the 1-form

 D

j D1

 x

on R

. Then

d D

j D1

^ dx

D !

248 Chapter VI. Questions, phenomena, results

is our canonical symplectic form on R

.IfuW R

! R

is a symplectic map of

, then the 1-form   u



 is closed, because

d.  u



/ D d  u



d D !

 u



D 0:

Thus, in view of the Poincaré lemma there exists a smooth function F W R

! R

satisfying

  u



 D dF:

Consequently, if  is a closed curve in R

, then



 





 D



dF D 0

and therefore



 D





 D

u./

:

The action of a closed curve  in .R

/ is deﬁned as the real number

A./ ´



:

We claim that a differentiable map uW R

! R

is symplectic if and only if

it leaves all actions invariant, that is,

A.u.// D A./

for all closed curves  of R

. Indeed, if u is symplectic, then

A./  A.u.// D



 

u./

 D 0;

as we have already seen. Conversely, if A./ D A.u.//, then



.  u



/ D 0

for all closed curves . Therefore, the 1-form u



 is exact and hence closed and

we conclude that !

u



D d d.u



/ D 0, as claimed. If  W Œ0; 1 ! R

is a closed curve so that .0/ D .1/, its action is represented as

A./ D

hJ P;idt

.; P/dt:

We return to the existence question of symplectic diffeomorphisms u W K

between two compact domains K

 R

having smooth boundaries @K

VI.4. A connection between geometry and Hamiltonian dynamics 249

and @K

. These boundaries are compact hypersurfaces.Ifu is a symplectic diffeo-

morphism of R

, then its linearized

duW L

! L

deﬁnes an isomorphism of the line bundles. Therefore u maps the characteristics

of @K

bijectively onto the characteristics of @K

.If

is a closed characteristic in

, then

A.u.

// D A.

Consequently, there exist symplectic invariants on the boundaries. We have numer-

ical conditions the domains K

and K

must satisfy, in order to be symplectically

diffeomorphic. The Hamiltonian ﬂows induced on the boundaries @K

and @K

must be equivalent up to reparametrization of the orbits. Therefore, the complete

Hamiltonian system on the boundary @K

is a symplectic invariant! This is why

we started with embeddings of open domains.

Finally, we present some examples of characteristics which will be useful later

on.

Examples. (1) Surface of a sphere. Let @B.R/ Dfz 2 R

jjxj

Cjyj

D R

be the sphere of radius R>0where z D .x; y/ 2 R

 R

. The Hamiltonian

systems deﬁned by the function

H.z/ D

.jxj

Cjyj

has the boundary @B.R/ Dfz j H.z/ D R

=2g as a regular and compact energy

surface. The Hamiltonian equation is linear and given by

Pz D J rH.z/ D Jz;

and the Hamiltonian ﬂow can be written explicitly as

.z/ D e

z D .cos t/z C .sin t/Jz:

All the solutions are periodic of the same period 2. The characteristics  on

the sphere @B.R/ are all closed and have the same actions equal to

A./ D

2

hJ Pz.t/; z.t/idt D

2

H.z.t//dt D R

(2) Symplectic cylinder. If Z.r/ Dfz 2 R

j x

g is the symplectic

cylinder we take the Hamiltonian function

H.z/ D

C y

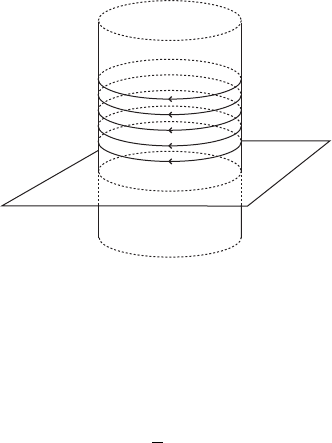
250 Chapter VI. Questions, phenomena, results

so that the boundary

@Z.r/ Dfz j x

C y

D r

gDfz j H.z/ D r

=2g

is a regular energy surface of the Hamiltonian system. The Hamiltonian equation

Pz D J rH.z/ D J.x

;0;:::;0;y

;0;:::;0/

is linear and looks explicitly as follows:

D y

;

Dx

;

D 0; 2  i  n;

D 0; 2  i  n:

We see that all the solutions on @Z.r/ are again periodic, lie on circles in planes

parallel to the plane E D spanfe

g and have the same action equal to

A./ D r

; @Z.r/:

Z.r/

E D spanfe

Figure VI.7. Some solutions on @Z.r/.

(3) Isotropic cylinder. If Z

iso

.r/ Dfz 2 R

j x

C x

g is the isotropic

cylinder, we take the Hamiltonian function

H.z/ D

C x

Then the boundary @Z

iso

.r/ Dfz j x

C x

D r

gDfz j H.z/ D r

=2g of the

cylinder is a regular energy surface. The Hamiltonian equation is again linear,

Pz D J rH.z/ D J.x

;0;:::;0/D .0;:::;0;x

; x

;0;:::;0/;