Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

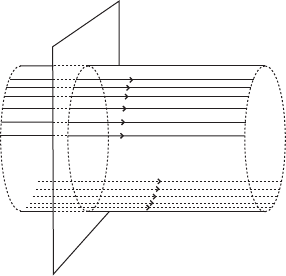
VI.4. A connection between geometry and Hamiltonian dynamics 251

and explicitly given by

Dx

;

Dx

;

D 0; 1  i  n;

D 0; 3  i  n:

This time the solutions are straight lines orthogonal to the plane E D spanfe

There are no closed characteristics and no ﬁnite actions!

iso

.r/

E D spanfe

Figure VI.8. Some solutions on @Z

iso

.r/.

In view of the examples above it is tempting to explain the non-squeezing

phenomenon of Gromov from the dynamical point of view as follows. On the

boundary @B.R/ of the open ball the characteristics are all closed and have actions

equal to R

. Similarly, on the boundary @Z

iso

.r/ of the symplectic cylinder

the characteristics are closed and their actions are equal to r

. If the map '

is a symplectic embedding of the closed ball of radius R, then on the boundary

of its image the characteristics are also closed and have actions equal to R

Imagine now that there is an optimal embedding of the open ball B.R/ into the

open symplectic cylinder, in which case one is inclined to think that the boundary

of the embedded ball touches the boundary of the cylinder and that this is happening

along a closed characteristic. We then conclude in view of the invariance of the

actions that r D R. A proof of the non-squeezing theorem of Gromov along these

lines does not exist and we shall prove it in the next chapter by means of a symplectic

invariant called symplectic capacity.

Chapter VII

Symplectic invariants

This chapter is devoted to a special class of invariants of symplectic manifolds,

introduced in the framework of subsets of the symplectic standard space .R

by I. Ekeland and H. Hofer [33] 1989 and [34] 1990. They are called symplectic

capacities. A symplectic capacity associates with every symplectic manifold a non-

negative real number or inﬁnity, so that three axioms are satisﬁed. In view of its

monotonicity axiom a symplectic capacity represents, in particular, an obstruction to

symplectic embeddings. The Gromov non-squeezing phenomenon is an immediate

consequence, as we shall ﬁrst demonstrate among other simple consequences. Then

we shall construct a special symplectic capacity c

, the so-called Hofer–Zehnder

capacity which is of dynamical nature. It measures the minimal oscillation of

Hamiltonian functions needed to conclude the existence of a fast periodic solution

of the associated Hamiltonian vector ﬁeld. In dimension 2, the capacity c

agrees

with the total area. The construction of c

is based on a variational principle for

the action functional of classical mechanics which is bounded neither below nor

above. Critical points can be guaranteed by mini-max arguments. The tools from

the calculus of variations will be developed in detail and from scratch. Applications

of the dynamical capacity c

to Hamiltonian vector ﬁelds are postponed to Chapter

VIII where it will be used to establish global periodic orbits on and near compact

hypersurfaces of symplectic manifolds.

VII.1 Symplectic capacities and ﬁrst applications

In the following we denote by SM.2n/ the class of all symplectic manifolds .M; !/

of dimension 2n. This includes compact and non-compact manifolds, manifolds

with boundaries and manifolds without boundaries. Examples are the symplectic

standard space .R

/, the manifold .U; !

/ where U  R

is an open subset,

the manifold .D; !

/ where D  R

is a domain having smooth boundaries, or

the same subsets of R

equipped with a different symplectic structure deﬁned by

a closed 2-form

!.x/ D

i;jD1

.x/dx

^ dx

;

where a

are smooth functions and where !.x/ is for every x a nondegenerate

skew symmetric bilinear form. In matrix notation,

!.x/.u; v/ DhJ.x/u; vi;

VII.1. Symplectic capacities and ﬁrst applications 253

with a skew symmetric matrix J.x/ DJ.x/

satisfying det J.x/ ¤ 0.

Deﬁnition. A symplectic capacity is a map

c W SM.2n/ ! Œ0; 1; .M; !/ 7! c.M;!/;

associating with a symplectic manifold of dimension 2n a non-negative real number

or inﬁnity, satisfying the following three axioms.

(A1) Monotonicity. If there exists a symplectic embedding .M; !/ ! .N; / into

a second symplectic manifold of dimension 2n, then

c.M;!/  c.N;/:

(A2) Conformality. For every symplectic manifold .M; !/ and for every real num-

ber ˛ ¤ 0 we have

c.M;˛!/ Dj˛jc.M;!/:

(A3) Normalization. If B.1/  R

is the open unit ball centered at the origin and

if Z.1/  R

is the symplectic open unit cylinder, then

c.B.1/; !

/ D  D c.Z.1/; !

We recall that B.R/ Df.x; y/ 2 R

 R

jjxj

Cjyj

g and Z.r/ D

f.x; y/ 2 R

 R

j x

C y

g with respect to the symplectic coordinates

.x; y/ D .x

;:::;x

;:::;y

/ of the symplectic standard space .R

/. The

map ' W .M; !/ ! .N; / is a symplectic embedding, if ' W M ! N is an injective

immersion satisfying '



 D !, and if ' W M ! '.M /  N is a homeomorphism

onto its image '.M/.

The three axioms (A1)–(A3) do not determine a unique capacity function. The

existence proof of a capacity function is neither trivial nor intuitive. We postpone

it for the moment, and assuming that the existence of a capacity is guaranteed, we

ﬁrst illustrate the concept and deduce some simple consequences.

Proposition VII.1. A symplectic capacity c is a symplectic invariant which differs

from the volume if n>1.

Proof [Monotonicity]. If ' W .M; !/ ! .N; / is a symplectic diffeomorphism,

then c.M;!/  c.N;/ in view of the monotonicity axiom (A1). Since the inverse

diffeomorphism '

1

W N ! M is also symplectic, the converse inequality holds

also true, so that c.M;!/ D c.N;/. From (A3) it follows that the volume is not a

symplectic capacity if n>1, because vol.Z.1// D1, while the capacity of Z.1/

is ﬁnite. 

254 Chapter VII. Symplectic invariants

In the special case n D 1, that is, dim M D 2, the total volume is an example

of a symplectic capacity c,

c.M;!/ D

; dim M D 2:

If, for instance, U  R

is an open set or a domain having smooth boundaries, then

c.U;!

/ D c.U;dx ^ dy/ Djarea.U /j is its symplectic capacity.

Lemma VII.2. If c is a symplectic capacity, U  .R

/ an open subset and

 ¤ 0 a real number, then

c.U;!

/ D 

c.U;!

Proof [Conformality]. This is a consequence of the conformality axiom. The dif-

feomorphism

' W U ! U; x 7! 

1

satisﬁes '



.

/ D 



D 



2

D !

: Therefore

' W .U; !

/ ! .U; 

is a symplectic diffeomorphism, so that

c.U;!

/ D c.U;

/ D 

c.U;!

by Proposition VII.1 and axiom (A2). 

Proposition VII.3. Let c be symplectic capacity. In the symplectic standard space

/ we have, for every r>0,

c.B.r// D r

;

B.r// D r

;

c.Z.r// D r

Proof. From Lemma VII.2 and (A3) we conclude

c.B.r// D c.rB.1// D r

c.B.1// D r

Analogously, one veriﬁes that c.Z.r// D r

.If">0, then B.r/  B.r/ 

B.r C "/ and, in view of the monotonicity axiom (A1),

r

D c.B.r//  c.B.r//  c.B.r C "// D .r C "/

This holds true for every ">0, so that c.

B.r// D r

, as claimed. 

VII.1. Symplectic capacities and ﬁrst applications 255

Remark. In R

it therefore follows for every symplectic capacity c that

c.B.r// D c.

B.r// D area.B.r//; n D 1:

One can conclude that for every bounded connected domain D  .R

/ with

smooth boundary, the symplectic capacity agrees with the area,

c.D/ D area.D/:

For a proof we refer to [52].

Proposition VII.4. If ;¤U  .R

/ is an open and bounded subset, then

0<c.U/<1

for every symplectic capacity c.

Proof. The set U contains a small open ball B

.r/ around a point x

2 U and

is contained in a large open ball B.R/ centered at 0. Since the translation in R

is a symplectic diffeomorphism, we have c.B

.r// D c.B.r// and conclude the

estimates

0<r

 c.U/  R

< 1

from the inclusions B

.r/  U  B.R/, using the monotonicity axiom. 

Examples. (1) If U  .R

/ is an open set satisfying

B.r/  U  Z.r/;

one concludes by the monotonicity and Proposition VII.3 for every symplectic

capacity c, that c.U / D r

– regardless of the volume, the geometrical properties

and the topological properties of U !

(2) Ellipsoid. We consider the ellipsoid E in .R

/ which is the set

E Dfz j q.z/<1gR

with the quadratic function q W R

! R deﬁned by

q.z/ D

j D1

C y

;zD .x

;:::;x

;:::;y

/ 2 R

where the constants r

D r

.E/>0are ordered according to 0<r

.E/ 

.E/. Then B.r

/  E  Z.r

/ and using the monotonicity one concludes that

the capacity of the ellipsoid is equal to c.E; !

/ D r

.E/

In view of their monotonicity properties the symplectic invariants c.M;!/ rep-

resent in particular obstructions to symplectic embeddings. For example, an imme-

diate consequence of the axioms is M. Gromov’s non-squeezing theorem.

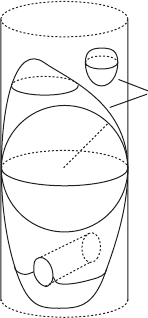
256 Chapter VII. Symplectic invariants

Z.r/

Figure VII.1. Illustration of example (1).

Theorem VII.5 (Gromov’s non-squeezing theorem, 1985). In the symplectic stan-

dard space .R

/ there exists a symplectic embedding

' W B.R/ ! Z.r/

if and only if r  R.

Proof [Monotonicity and normalization]. If r  R, then the inclusion map

B.R/ ,! Z.r/ is a symplectic embedding. Conversely, if ' W B.R/ ! Z.r/

is a symplectic embedding and if c is a symplectic capacity (whose existence

will be proved later), then the monotonicity and Proposition VII.3 lead to R

c.B.R//  c.Z.r// D r

, so that r  R, as claimed in the theorem. 

In view of the monotonicity and the example above the following statement is

obvious.

Theorem VII.6. Let E and F be two ellipsoids in .R

/. If there exists a

symplectic embedding ' W E ! F , then r

.E/  r

.F /.

Theorem VII.7. In .R

/  .R

/ there exists a symplectic diffeomorphism

' W B.r

/  B.r

/ ! B.s

/  B.s

between products of open 2-discs satisfying r

 r

and s

 s

, if and only if

D s

and r

D s

Proof. We denote by B

.r/ the open ball in R

centered at the origin. If ' is the

symplectic diffeomorphism of the theorem, we consider the following composition

VII.1. Symplectic capacities and ﬁrst applications 257

of mappings:

! B

/  B

! B

/  B

! B

/  R

D Z.s

where i and j are the inclusion mappings. The composition j B ' B i W B

/ !

Z.s

/ is a symplectic embedding so that s

 r

in view of Theorem VII.5. The

same argument applied to the inverse map '

1

leads to r

 s

, so that r

D s

Because ' is volume preserving, it follows that r

D s

, as claimed. 

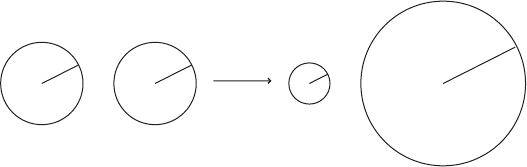
1=r



Figure VII.2. In view of Theorem VII.7 such a symplectic embedding is not possible.

The previous theorem shows clearly that volume preserving diffeomorphisms

behave completely differently from symplectic diffeomorphisms. For every r>0

there exists a (linear) volume preserving diffeomorphism

B.1/  B.1/ ! B.r/  B.1=r/:

The volume vol.B.r/  B.1=r// D 

is independent of r. In contrast, the sym-

plectic capacity function satisﬁes c



B.r/  B.1=r/



D r

! 0 as r ! 0.

We have already seen above that every open ball B.R/ can be symplectically

embedded into the isotropic cylinder Z

iso

.r/ Dfz 2 R

j x

C x

g

/. As a consequence its capacity is easily computed.

Proposition VII.8. c.Z

iso

.r/; !

/ D1for every r>0and for every symplectic

capacity c.

Proof [Monotonicity]. Take the symplectic diffeomorphism '.x; y/ D ."x; "

1

for .x; y/ 2 R

 R

where ">0.IfR>0, then for " sufﬁciently small

' W B.R/ ! Z

iso

.r/

is a symplectic embedding and hence, in view of the monotonicity property of the

capacity,

R

D c.B.R//  c.Z

iso

.r//:

This holds true for every R>0and so c.Z

iso

.r// D1, as claimed. 

258 Chapter VII. Symplectic invariants

If one symplectic capacity has been found, it is easy to construct new ones.

One example is the Gromov width G.M; !/ of a symplectic manifold which will

be introduced next.

We consider the symplectic manifold .M; !/ of dimension 2n. Given an open

subset U  M there exists in view of Darboux’s theorem a symplectic embedding

' W .B.r/; !

/ ! .U; !/;

of an open ball in R

having a sufﬁciently small radius r>0. We now look for

the largest open ball that can be symplectically embedded into the given manifold.

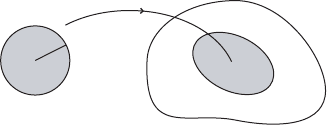
Deﬁnition. The Gromov width G.M; !/ is deﬁned as

G.M; !/Dsupfr

j there exists a symplectic embedding .B.r/; !

/ !.M; !/g:

Figure VII.3. Embedding of the open ball B.r/, illustrating the deﬁnition of the Gromov

width.

Theorem VII.9. The Gromov width G.M; !/ is a symplectic capacity. It satisﬁes

G.M; !/  c.M;!/

for every capacity c and every symplectic manifold .M; !/.

Proof [Gromov]. We shall verify that the function G satisﬁes the axioms (A1)–(A3)

of a capacity function.

(A1) Let W .M; !/ ! .N; / be a symplectic embedding. For every symplec-

tic embedding ' W B.r/ ! M into M the composition

B ' W B.r/ ! N

is a symplectic embedding into M . In view of the deﬁnition of the function G it

therefore follows that G.N; /  G.M; !/ and hence the axiom (A1) is veriﬁed.

(A2) Let 0 ¤ ˛ 2 R. We show that to every symplectic embedding

' W .B.r/; !

/ ! .M; ˛!/

VII.1. Symplectic capacities and ﬁrst applications 259

there belongs a symplectic embedding

O' W



j˛j



! .M; !/

and conversely. Then the property G.M; ˛!/ Dj˛jG.M; !/ of axiom (A2) fol-

lows.

If ' W .B.r/; !

/ ! .M; ˛!/ is a symplectic embedding, then '



.˛!/ D

˛'



! D !

and so



! D

Abbreviating ı D

j˛j

, the map

W .B.ı/; !

/ !



B.r/;



; .x/ ´

j˛jx

satisﬁes









j˛j

D sign.˛/ !

If sign.˛/ DC1, the composition

O' D ' B W .B.ı/; !

/ ! .M; !/

is a symplectic embedding, because



! D



B '



! D







D sign.˛/!

D !

If sign.˛/ D1, we take the symplectic diffeomorphism

W .B.ı/; !

/ ! .B.ı/; !

deﬁned by

.x; y/ D .x; y/ for .x; y/ 2 R

 R

, so that the composition

O' D ' B B

W .B.ı/; !

/ ! .M; !/

is a symplectic embedding as we wanted to show.

(A3) In order to conﬁrm the normalization axiom, we ﬁrst verify that

G.B.1/; !

/ D .If' W B.r/ ! B.1/ is a symplectic embedding, it follows

from the volume preservation that r  1 and hence G.B.1//  . Since the

inclusion map B.1/ ,! B.1/ is a symplectic embedding, G.B.1// D ,aswe

wanted to show. It remains to prove that G.Z.1/; !

/ D .If' W B.r/ ! Z.1/ is

a symplectic embedding, then, in view of the non-squeezing theorem, r  1 (here

we have made use of the existence of a capacity!) and hence G.Z.1/; !

/  .

The equality follows from the inclusion mapping. So far we have veriﬁed that the

260 Chapter VII. Symplectic invariants

Gromov width G is a symplectic capacity function and it remains to prove that it is

the smallest capacity.

Take any symplectic capacity function c and let ' W B.r/ ! M be a symplectic

embedding. Then, by the monotonicity property and Proposition VII.3,

r

D c.B.r/; !

/  c.M;!/:

This holds true for all the symplectic embeddings ' W B.r/ ! M and hence also for

the supremum. Consequently, G.M; !/  c.M;!/ and Theorem VII.9 is proved.



In the following sections we shall establish the existence of a capacity function.

We shall construct a very distinguished symplectic capacity c

related to the dy-

namics of Hamiltonian systems and introduced in 1990 by H. Hofer and E. Zehnder

[51]. This dynamical capacity measures the minimal oscillation of special Hamil-

tonian functions needed to conclude the existence of a distinguished fast periodic

solution of the associated Hamiltonian vector ﬁeld. In dimension 2 it agrees with

the total area. The construction is based on a variational principle for the classical

action functional of mechanics for periodic solutions of Hamiltonian equations.

VII.2 The Hofer–Zehnder capacity c

We recall that if .M; !/ is a symplectic manifold, then the smooth function H W M !

R determines the Hamiltonian vector ﬁeld X

on M by the requirement that

!.X

.x/; v/ DdH.x/v for all tangent vectors v 2 T

M .Aperiodic solu-

tion x.t/ of X

having period T is a solution of the equation

Px.t/ D X

.x.t//; t 2 R;

satisfying x.0/ D x.T /. Consequently, x.t C T/ D x.t/ for all t 2 R.Wenext

introduce a distinguished class of Hamiltonian functions.

Deﬁnition. If .M; !/ is a symplectic manifold we denote by H.M; !/ the set of

smooth functions H W M ! R having the following properties.

There exist an open set U  M and a compact set K  M (these sets depend

on H ) satisfying U  K  M n@M and

(i) H j

 0 is constant,

(ii) H j

M nK

 m.H / is constant,

(iii) 0  H.x/  m.H / for all x 2 M .

The constant m.H / D max H min H is the oscillation of the function H .A

function H 2 H.M; !/ is called admissible, if the associated Hamiltonian equation

Px D X

.x/ does not admit a non-constant periodic solution of period 0<T  1,

so that a periodic solution is either