Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

VII.2. The Hofer–Zehnder capacity c

261

(i) constant, x.t/ D x.0/ for all t 2 R,orhas

(ii) minimal period T>1.

We denote by H

.M; !/ the set of admissible functions in H.M; !/.

m.H /

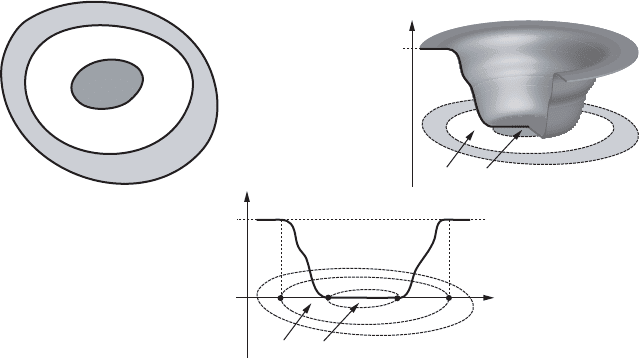
Figure VII.4. A function H 2 H.M; !/ with oscillation m.H /.

If H 2 H.M; !/ n H

.M; !/ ¤;, then the Hamiltonian vector ﬁeld Px D

.x/ possesses a non-constant periodic solution of period 0<T  1. Since H

vanishes on U and on M nK, the non-constant periodic solution must be contained

in K n U .

If the manifold M is compact without boundary, one can choose K D M .In

this case, H 2 H.M; !/ if the function H vanishes on an open set and satisﬁes

H  0.

Deﬁnition. The symplectic capacity c

of .M; !/ is deﬁned as

.M; !/ D supfm.H / j H 2 H

.M; !/g:

In the literature, this capacity c

is called Hofer–Zehnder capacity. We shall

show that c

is, indeed, a symplectic capacity function.

The capacity function c

has the following signiﬁcance. If c

.M; !/ < 1, then

for every function H 2 H.M; !/ satisfying m.H / > c

.M; !/, the Hamiltonian

vector ﬁeld X

on M possesses at least one non-constant periodic solution of period

0<T  1. In fact, c

.M; !/ is the inﬁmum over all numbers having this property.

The proof of the next theorem will take up the rest of the chapter.

262 Chapter VII. Symplectic invariants

'.M /

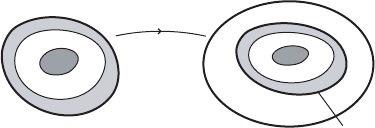
Figure VII.5. Illustrating the veriﬁcation of the monotonicity axiom.

Theorem VII.10 (Hofer–Zehnder). The map c

W .M; !/ 7! c

.M; !/ is a sym-

plectic capacity.

We shall illustrate the theorem with the open ball B.r/. From c

.B.r/; !

/ D

r

it follows for every function H 2 H.B.r/; !

/ satisfying m.H / > r

that

the Hamiltonian vector ﬁeld X

has a periodic solution of period 0<T  1.If

r D 1 we obtain, by way of the capacity c

, a dynamical deﬁnition of the number

 in terms of periodic solutions of Hamiltonian systems.

We point out that in dimension 2 the special capacity c

agrees with the area,

so that c

.U; !

/ D area U ,ifU  R

and

.M; !/ D

; dim M D 2:

This result is due to K. F. Siburg [104] and M.Y. Jiang [54], it can also be found in

the book [52].

In order to prove Theorem VII.10, we have to verify that the function c

meets

the axioms (A1)–(A3). It turns out that the monotonicity and the conformality

of c

easily follow from the deﬁnition. The difﬁculty is the veriﬁcation of the

normalization axiom (A3), that is, the computation of the values of c

for the

cylinder Z.1/ and the ball B.1/ equipped with the canonical symplectic structure.

We begin with the monotonicity.

Lemma VII.11. The map c

satisﬁes the monotonicity axiom (A1).

Proof. If ' W .M; !/ ! .N; / is a symplectic embedding, we have to prove that

.M; !/  c

.N; /. In view of the deﬁnition of c

it sufﬁces to verify that for

every function H 2 H

.M; !/ on M , there exists a function H

2 H

.N; / on

N having the same oscillation, that is, m.H

/ D m.H /.

We deﬁne the map '



W H.M; !/ ! H.N;  / by



.H /.x/ ´

H B '

1

.x/; x 2 '.M/;

m.H /; x … '.M/:

VII.2. The Hofer–Zehnder capacity c

263

Since K  M n @M is compact, also its image '.K/  N n @N is compact.

Moreover, the set '.M n@M / is open in N and the sets '.K/ and N n'.M n@M / can

be separated in N by open sets, so that the function '



H is a smooth function on N .

In addition, '.U /  N is open and we see that '



H 2 H.N; /. By construction,

m.'



.H // D m.H /. It only remains to show that '



.H / is admissible, if H is

admissible. Since ' is a symplectic map,





.H /

D X



.H /B'

D X

;

in view of Proposition V.26. Consequently, the ﬂows are conjugated in the sense

that

' B '

B '

1

D '



.H /

In particular, all the corresponding periodic solutions have the same periods. 

Lemma VII.12. The map c

satisﬁes the conformality axiom (A2).

Proof. If ˛ ¤ 0, we have to show that c

.M; ˛!/ Dj˛jc

.M; !/. For this purpose

we deﬁne the bijection W H.M; !/ ! H.M; ˛!/ by

H 7!j˛jH μ H

Clearly,

m.H

/ Dj˛jm.H /;

so that the lemma follows if we show that also deﬁnes a bijection

W H

.M; !/ ! H

.M; ˛!/

between the admissible functions. By the deﬁnition of the Hamiltonian vector

ﬁelds,

.˛!/.X

; / DdH

Dj˛jdH Dj˛j!.X

; /

so that



j˛j

; 



D !.X

; /:

Due to the nondegeneracy of ! we obtain

j˛j

D X

on M and so

D˙X

In both cases the vector ﬁelds have the same periodic orbits and the corresponding

periods are the same. This completes the proof of Lemma VII.12. 

The next lemma is the ﬁrst step towards the veriﬁcation of axiom (A3).

Lemma VII.13. c

.B.1/; !

/  .

264 Chapter VII. Symplectic invariants



  "

Figure VII.6. The function f W Œ0; 1 ! R.

Proof. We show that for every 0<"<there exists an admissible function

H 2 H

whose oscillation is equal to m.H / D   " which then proves the

lemma. For this purpose we ﬁrst choose a C

-function f W Œ0; 1 ! R having the

following properties, illustrated by Figure VII.6,

(i) f.t/ D 0 for t near 0,

(ii) f.t/ D   " for t near 1,

(iii) 0  f.t/    " for all t,

(iv) 0  f

.t/<for all t .

The Hamiltonian function H W B.1/ ! R is deﬁned by

H.x/ D f.jxj

From the properties of f we conclude that H 2 H.B.1/; !

/ and

m.H / D   ";

so that the proof is complete, if we show that H belongs to the set H

.B.1/; !

/ of

admissible functions. The associated Hamiltonian vector ﬁeld X

, explicitly given

Px D J rH.x/ D 2f

.jxj

/Jx;

has the function G.x/ D

jxj

as an integral, because

dG.x/X

.x/ DhrG.x/; X

.x/iD2f

.jxj

/ hx;JxiD0:

Consequently, for every solution x.t/ the value of the function 2G.x.t// Djx.t/j

and hence also the value of the function 2f

.jx.t/j

/ μ a.x.0// is constant in time

t along the solution. Therefore, every solution x.t/ solves the linear equation

Px D aJ x;

VII.2. The Hofer–Zehnder capacity c

265

for a real number a  0, and so is equal to x.t/ D e

atJ

x.0/ D .cos at/x.0/ C

.sin at/J x.0/. We see that all the solutions are periodic! In the case a D 0, the

solution is constant D x.0/, in the case a>0the solution has the minimal period

T D 2=a. From 0  f

<, it follows that a<2and hence T>1.We

have veriﬁed that the function H does, indeed, belong to the set H

of admissible

functions. 

We have demonstrated the estimate c

.B.1/; !

/   by means of a single

example. Since the inclusion map B.1/ ,! Z.1/ is a symplectic embedding, we

obtain, in view of Lemma VII.11, the following estimate.

Corollary VII.14.   c

.B.1//  c

.Z.1//.

In order to verify the normalization axiom (A3), it remains to prove the estimate

.Z.1//  . This requires an existence proof, namely, the proof of the following

theorem. If proved, Theorem VII.10 is also proved and c

is a symplectic capacity,

as claimed.

Theorem VII.15. If H 2 H.Z.1// satisﬁes m.H / > , then the Hamiltonian

vector ﬁeld X

on Z.1/ possesses a non-constant periodic solution x.t/ 2 Z.1/

of period T D 1.

It follows that c

.Z.1//  , so that Theorem VII.10 is proved.

It remains to ﬁnd a global periodic solution of period T D 1, for a Hamiltonian

vector ﬁeld X

deﬁned on the open cylinder Z.1/ where the Hamiltonian function

H belongs to the set H.Z.1/; !

/ and satisﬁes m.H / > .

Our existence proof will be based on a variational principle for the action func-

tional of classical mechanics and we start with some preparations.

Since the Hamiltonian function H W Z.1/ ! R belongs to H.Z.1/; !

/ it satis-

ﬁes H  0 on an open set U and H  m.H / is constant outside of a compact set K

that contains U . We have already proved that c

is a symplectic invariant, because

the monotonicity axiom (A1) holds true for c

. Therefore, we may assume that U

is an open neighborhood of 0 2 R

by means of a symplectic diffeomorphism of

having compact support in the cylinder Z.1/.

We prefer to work with a Hamiltonian function deﬁned on the whole space R

and not merely on the cylinder Z.1/ and we therefore extend the function H to

a smooth function

H W R

! R. In principle, this is not a problem, we could,

for instance, extend H by the constant m.H /. For technical reasons, this is not

good enough and we shall choose a more clever extension which, far away from

the origin, looks like a speciﬁc quadratic form.

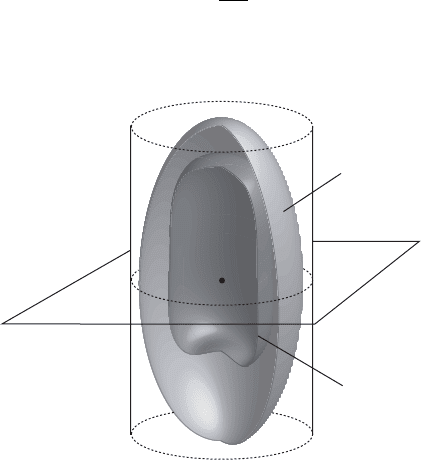
Since the set K  Z.1/ is compact, there exists an ellipsoid E D E

 Z.1/

containing the compact set K  E, so that the Hamiltonian function H also belongs

to the set H.E; !

/. Indeed, we choose

E Dfz 2 R

j q.z/<1g

266 Chapter VII. Symplectic invariants

for z D .x; y/ 2 R

 R

, with the quadratic function q deﬁned by

q.z/ D x

C y

j D2

C y

and choose the integer N sufﬁciently large.

Z.1/

Figure VII.7. The ellipsoid E D E

around the compact set K  Z.1/.

We have to keep in mind that q is homogeneous of degree 2, so that

q.z/ D 

q.z/

for all  2 R and z 2 R

. Differentiating this equation in the variable  at the

point  D 1 we obtain the identity

hrq.z/; ziD2q.z/; z 2 R

By assumption, the function H possesses the oscillation m.H / >  and we

choose a small constant ">0such that

m.H / >  C ":

Next, we choose a C

-function f W R ! R, illustrated in Figure VII.8, having the

following properties:

(i) f.s/ D m.H / for s  1,

(ii) f.s/  . C "/s for all s 2 R,

VII.2. The Hofer–Zehnder capacity c

267

m.H /

 C "

Figure VII.8. The function f W R ! R.

(iii) f.s/ D . C "/s for s large,

(iv) 0<f

.s/   C " for s>1.

The extension

H of the Hamiltonian H is ﬁnally deﬁned as the function

H.z/ D

H.z/; z 2 E;

f .q.z//; z … E:

The function

H is a non-negative smooth function on R

which is quadratic

at inﬁnity in the sense that

H.z/ D . C "/q.z/; jzjR

for a sufﬁciently large R.

We are looking for periodic solutions of the extended Hamiltonian vector ﬁeld

which are contained in the ellipsoid E, where the vector ﬁeld X

agrees with

the original vector ﬁeld X

. For this purpose the following a-priori statement is

crucial. It localizes the distinguished periodic solutions we are looking for.

Lemma VII.16. If x.t/ is a periodic solution of the Hamiltonian vector ﬁeld Px D

.x/ of period 1 which satisﬁes

ˆ.x/ ´

hJ Px.t/; x.t/i

H.x.t//dt > 0;

then x.t/ is non-constant and lies in the ellipsoid E for all t . In particular x.t/ is

a non-constant 1-periodic solution of the original system Px D X

.x/ in the open

cylinder Z.1/.

268 Chapter VII. Symplectic invariants

Proof. If x.t/ D x



is a constant solution, then ˆ.x



/  0, because Px D 0

and

H.x/  0. It remains to prove for a non-constant periodic solution x.t/ of

Px D X

.x/ that ˆ.x/  0,ifx.t/ is not contained in E for all t.

The Hamiltonian vector ﬁeld X

vanishes on the boundary @E Dfz j q.z/ D

1g, because f

.1/ D 0. Therefore, if a solution x.t/ satisﬁes x.t

/ … E for some

2 R, then x.t/ … E for all t and there x.t/ solves the equation

Px D X

.x/ D J r

H.x/ D f

.q.x// J rq.x/; x  R

However, outside of the ellipsoid E the function q is an integral of the vector ﬁeld

, since here

hrq; J r

H iDhrq; J rqif

.q/ D 0:

Consequently along the solution x.t/ in

Dfq>1g, the function

q.x.t// D q.x.0// μ >1

is independent of t. Recalling that hrq.x/; xiD2q.x/ for all x 2 R

, and using

D1, and the properties of the function f , we compute

ˆ.x/ D

hJ Px.t/; x.t/i

H.x.t//dt

./ hrq.x/; xidt 

f.q.x//dt

./2q.x.t// dt  f./

D f

./  f./

 . C "/  . C "/

D 0:

Hence ˆ.x/  0 for all solutions x not contained in E and the lemma is proved.



In view of this lemma our task is now the following.

• Find a 1-periodic solution of Px D X

.x/ in R

satisfying ˆ.x/ > 0!

To simplify the notation, we shall in the following again write H instead of

H ,

H instead of

H .

In order to establish the existence of a periodic solution we shall make use of a well-

known variational principle for which the critical points are the required periodic

solutions. In order to introduce this principle we proceed at ﬁrst on an informal

level and consider the loop space of smooth closed curves

 D C

; R

VII.2. The Hofer–Zehnder capacity c

269

where S

D R=Z. On this loop space we deﬁne the functional ˆ W  ! R by

setting

ˆ.x/ ´

hJ Px.t/; x.t/iH.x.t//dt:

The functional ˆ is the action functional of classical mechanics.

Claim. The critical points of the functional ˆ are precisely those loops that solve

the Hamiltonian equation Px D X

.x/, so that the critical points are the 1-periodic

solutions of X

Proof. The derivative of the functional ˆ at the loop x 2  in the direction of

y 2  is easily computed,

.x/y ´

ˆ.x C "y /

"D0

hJ Py.t/; x.t/iC

hJ Px.t/; y.t/ihrH.x.t//;y.t/idt:

By partial integration we obtain

hJ Py; xiD

hJy; PxiD

hy; J

PxiD

hy; J Pxi;

because the boundary terms cancel each other due to the periodicity of x and y.

Therefore,

.x/y D

hJ Px rH.x/;yidt:

If x is a critical point of ˆ, that is, if

.x/.y/ D 0 for all y 2 ;

then, necessarily J Px.t/ rH.x.t// D 0 for all t and hence

Px.t/ D J rH.x.t// D X

.x.t// for all t 2 R and x.0/ D x.1/:

We see that the critical points are precisely those loops that are 1-periodic solutions

of the Hamiltonian equation, as claimed. 

From the potentially extremely complicated set of solutions of the Hamiltonian

system the variational principle selects precisely the 1-periodic solutions. We are

dealing with a global boundary value problem with periodic boundary conditions.

Unfortunately, we are confronted with a difﬁculty. The functional ˆ is neither

bounded below nor bounded above, so that the so-called direct methods of the

calculus of variation based on minimizing sequences are not applicable.

270 Chapter VII. Symplectic invariants

Example. We take a sequence of loops x

2 , deﬁned by

.t/ D e

j2Jt

D .cos j2t/x

C .sin j 2t/J x

for a constant x

2 R

satisfying jx

jD1; so that kx

D 1 for all j 2 Z.For

the ﬁrst term of the action functional we compute

hJ Px

.t/; x

.t/idt D

hJ

j2e

j2Jt

idt D j;

while the second term is bounded,

H.x

.t// dt

 sup

jzjD1

jH.z/j:

Hence, ˆ.x

/ !1as j !1and ˆ.x

/ !1as j !1.

In view of these examples it is useless to search for global maxima or minima

and the task is to ﬁnd saddle points. Only relatively recently, P. Rabinowitz [89]

and [90] demonstrated that our degenerate variational principle can be used very

effectively for existence proofs. For this purpose he designed minimax arguments

adapted to the structure of the functional. Before we start with the technical details

for the functional ˆ, it is helpful to describe the minimax idea ﬁrst in an abstract

setting.

VII.3 Minimax principles

We assume E to be a real Hilbert space having the scalar product h; i and the

induced norm kkDh; i

1=2

and let f W E ! R be a C

-function. We are

looking for critical points of the function f . By deﬁnition these are points x



2 E

satisfying

df . x



/ D 0;

so that df . x



/y D 0 for all y 2 E. The derivative df . x



/ is an element of the dual

space E



D L.E; R/ which is the space of continuous linear functionals equipped

with the supremum norm. In view of a well-known theorem by F. Riesz there exists

a distinguished linear surjective isometry

I W E



! E; e



7! I.e



such that the linear functional e



2 E



has a unique representation as the scalar

product



.y/ DhI.e



/; yi for all y 2 E