Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.


VIII.1. Global periodic solutions on prescribed energy surfaces 311
we choose the auxiliary function f 2 C
1
.R; R/, illustrated in Figure VIII.2 and
satisfying
f.s/ D c
0
.M; U / C 1; s "; s ";
f.s/ D 0; "=2 s "=2;
f
0
.s/<0; "<s<"=2;
f
0
.s/>0; "=2<s<":
f
s
""=2"=2"
c
0
.U / C 1
Figure VIII.2. The auxiliary function f W R ! R.
The smooth function F W U ! R is now defined by
F.x/ ´ f .H.x//;
and satisfies F 2 H.U; !/, since H.x/ D on S
. Moreover,
m.F / > c
0
.U; !/:
Consequently, in view of the definition of the capacity c
0
there exists a non-constant
periodic solution x.t/ of the Hamiltonian equation
Px D X
F
.x/
F
m.F /
0
S
U
Figure VIII.3. The function F D f B H on the neighborhood U M of S.
312 Chapter VIII. Applications of the capacity c
0
in Hamiltonian systems
in U , having period 0<T 1. We claim that
X
F
.x/ D f
0
.H.x// X
H
.x/; x 2 U:
Indeed, in view of the definition of Hamiltonian vector fields we compute
!.X
F
.x/; / DdF .x/
Df
0
.H.x// dH.x/
D !
f
0
.H.x// X
H
.x/;
;
and the claim follows as ! is nondegenerate. From dH .X
F
/ D!.X
H
;X
F
/ D 0
we deduce that the function H is an integral of the vector field X
F
. Hence, H is
constant along the periodic solution x.t/ of X
F
, so that H.x.t// μ is indepen-
dent of t. Thus, also the function f
0
.H.x.t/// D f
0
./ μ is independent of t
and since x.t/ is a non-constant solution of X
F
, the constant satisfies ¤ 0.In
view of the definition of the auxiliary function f , the parameter is necessarily
contained either in the interval ."; "=2/ or in ."=2; "/, in particular jj <".
Reparametrizing, the curve
y.t/ ´ x.t=/
is a solution of X
H
, because
Py.t/ D
1
Px.t=/
D
1
X
F
.x.t=//
D
1
f
0
.H.x.t= /// X
H
.x.t=//
D
1
X
H
.y.t //:
This solution y.t/has period jjT>0and, due to H.y.t// D H.x.t=// D ,
lies on the energy surface S
. This completes the proof of the theorem.
If c
0
.U; !/ is finite, there exists in view of Theorem VIII.2 a sequence
j
! 0
such that every energy surface S
j
carries a periodic solution x
j
.t/ of period T
j
.
This raises the question whether these solutions converge to a periodic solution on
the given surface S D S
0
. Under the additional assumption that the periods T
j
are bounded, the answer is affirmative. Instead of assuming the periods T
j
to be
bounded, we can equivalently assume that the arc length of the periodic orbits x
j
.t/
with respect to any Riemannian metric are bounded. Indeed, if T is the minimal
period of a solution x.t/, then
l.x/ D
Z
T
0
jPxjdt D
Z
T
0
jX
H
.x.t//jdt
is the arc length with respect to the Riemannian metric. Since the neighborhood U
of the compact surface S is relatively compact, the Hamiltonian vector field satisfies
the estimate
c
1
jX
H
.x/jc; x 2 U
VIII.1. Global periodic solutions on prescribed energy surfaces 313
for a constant c>0, from which we deduce the estimate c
1
T l.x/ cT for
the arc length of the periodic solution x.t/ which proves the claim.
Proposition VIII.3. We consider the family .S
/
2I
of compact regular energy
surfaces of the Hamiltonian vector field X
H
in the open neighborhood U as de-
scribed in Theorem VIII.2. We take a converging sequence
j
!
in the interval
I having the property that every S
j
carries a periodic solution x
j
.t/ of period
T
j
>0. Then, if these periods are bounded, so that T
j
C for all j , there exists
a periodic solution on S
of period 0<T C .
Proof [Arzela–Ascoli]. Normalizing the periods to 1, we introduce the 1-periodic
orbits
y
j
.t/ ´ x
j
.T
j
t/; 0 t 1;
which solve the equations
./ Py
j
.t/ D T
j
X
H
.y
j
.t//
and satisfy H.y
j
.t// D
j
. Choosing a Riemannian metric and using that the
periods are bounded, we see that the derivatives are uniformly bounded,
jPy
j
.t/jDjT
j
X
H
.y
j
.t//jC sup
x2U
jX
H
.x/j < 1:
Therefore we find, by means of the Arzela–Ascoli theorem, a subsequence such
that T
j
! T and y
j
! y with convergence in the C
0
-sense. Iteratively using the
equations ./, we obtain the convergence y
j
! y in the C
1
-sense. The limit y.t/
is a 1-periodic solution of the equation
Py.t/ D TX
H
.y.t //;
which satisfies H.y.t// D
, and it remains to prove that T ¤ 0. Arguing by
contradiction we assume that T D 0, then y.t/ y
is constant and since S
is
a regular energy surface,
X
H
.y
k
.t// ! X
H
.y
/ μ v ¤ 0
for all t. We can estimate in local coordinates near the point y
,
T
1
k
hPy
k
.t/; viDhX
H
.y
k
.t//; vi.1 "/jvj
2
for some small and positive " and for all k large. Integrating over the period one
concludes jvjD0, contradicting v ¤ 0 and proving the proposition.
Going back to the statement of Theorem VIII.2, we shall show that the set
ƒ I of the parameters whose energy surfaces carry a periodic solution, is not only
dense, but has full Lebesgue measure. This result has been proved by H. Hofer and
314 Chapter VIII. Applications of the capacity c
0
in Hamiltonian systems
E. Zehnder in [52] under the additional assumption that the energy surface S M
is the boundary of a symplectic manifold. The proof combines the monotonicity of
the capacity with the classical result due to Lebesgue which states that a monotonic
function f W R ! R is differentiable in almost every point. That this additional
assumption on S is superfluous has recently been observed by L. Macarini and
F. Schlenk in [64].
TheoremVIII.4 (Macarini–Schlenk). Let S Dfx 2 M j H.x/ D 0gbe a compact
and regular energy surface of the Hamiltonian vector field X
H
on the symplectic
manifold .M; !/ and denote by
U D
[
2I
S
the bounded open neighborhood of S from Proposition VIII.1 where I D ."; "/
is an open interval. If
c
0
.U; !/ < 1;
then there exists a subset ƒ 2 I of full Lebesgue measure m.ƒ/ D m.I / such that
for every parameter 2 ƒ the associated energy surface S
carries a periodic
orbit of X
H
.
Proof. We denote by ƒ
n
I D ."; "/ the set of parameters , for which S
carries a periodic solution of period 0<T n. Due to Proposition VIII.3 the set
ƒ
n
is closed. So, ƒ D
S
n1
ƒ
n
is a countable union of Lebesgue-measurable sets
and, therefore, measurable. In order to show that ƒ has full measure we define for
0<˛<"the open subsets
U
˛
´
[
jj<˛
S
\ U Dfx 2 U j˛<H.x/<˛g
of U .
Lemma VIII.5. We assume that the increasing function ˛ 7! c
0
.U
˛
/ 2 R satisfies
at the point 0<˛
<"the Lipschitz estimate
c
0
.U
˛
/ c
0
.U
˛
/ C L.˛ ˛
/
for all ˛ ˛
and j˛ ˛
j sufficiently small and with a constant L>0. Then
˛
2 ƒ or ˛
2 ƒ.
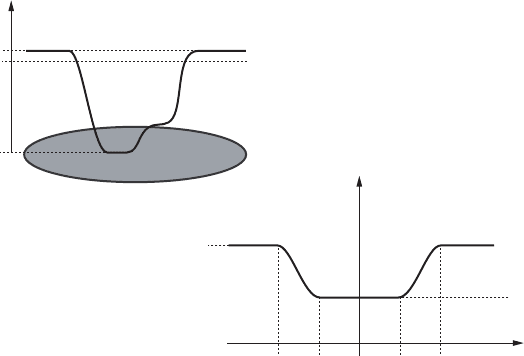
Proof. (1) Fix an ˛>˛
. By definition of the capacity c
0
there exists an admissible
Hamiltonian function G 2 H
a
.U
˛
/ having the oscillation
m.G/ > c
0
.U
˛
/ .˛ ˛
/:
VIII.1. Global periodic solutions on prescribed energy surfaces 315
We choose a smooth auxiliary function f W R ! R illustrated in Figure VIII.4 and
satisfying
f.s/ D
´
c
0
.U
˛
/ C .˛ ˛
/; s ˛ oder s ˛;
m.G/; s 2 Œ˛
;˛
;
and moreover,
f
0
.s/ < 0;s 2 .˛; ˛
/;
f
0
.s/ > 0;s 2 .˛
;˛/;
jf
0
.s/j <L
0
;s 2 R:
f
x
˛˛˛
˛
m.G/
m.G/
c
0
.U
˛
/ C .˛ ˛
/
c
0
.U
˛
/ .˛ ˛
/
G
0U
˛
Figure VIII.4. Left: The function G 2 H
a
.U
˛
/ with an oscillation m.G/ > c
0
.U
˛
/
.˛ ˛
/. Right: The auxiliary function f W R ! R.
In view of the Lipschitz assumption on the capacity function c
0
.U
˛
/, the auxiliary
function f can be chosen in such a way that the constant L
0
is equal to L C 3
independent of the choice of ˛>˛
. Now we define the smooth function F W M !
R (cf. Figure VIII.5)by
F.x/ D
´
f .H.x//; x … U
˛
.H.x/ ˛
and H.x/ ˛
/;
G.x/; x 2 U
˛
.˛
<H.x/<˛
/:
Then F is a smooth function belonging to the distinguished set H.U
˛
/ and has the
oscillation m.F / D c
0
.U
˛
/ C.˛ ˛
/>c
0
.U
˛
/. Consequently, by the definition
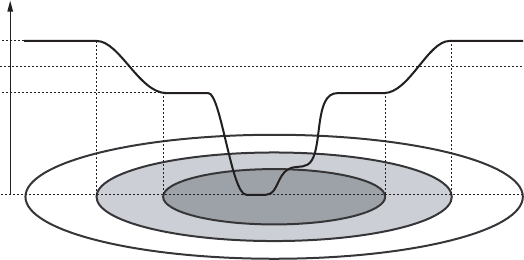
316 Chapter VIII. Applications of the capacity c
0
in Hamiltonian systems
F
U
˛
U
˛
M
0
m.G/
m.F /
c
0
.U
˛
/
Figure VIII.5. The Hamiltonian function F with oscillation m.F / > c
0
.U
˛
/.
of c
0
, the Hamiltonian vector field Px D X
F
.x/ has a non-constant periodic solution
x.t/of period 0<T 1 in U
˛
. Since the function G belonging to the set H.U
˛
/ is
an admissible function on U
˛
, the vector field X
G
does not admit a non-constant
periodic solution of period 0<T 1 in U
˛
. Therefore, x.t/ lies in the set
U
˛
n U
˛
. As in the proof of Theorem VIII.2 one verifies that
X
F
.x/ D f
0
.H.x// X
H
.x/; if x … U
˛
;
and that the Hamiltonian function H is constant along the periodic solution x.t/.
In view of the definition of the auxiliary function f , the solution x.t/ lies on an
energy surface S
or S
for a parameter contained in the open interval .˛
;˛/
and the constant f
0
.H.x.t/// μ satisfies 0<<L
0
. As in the proof of
Theorem VIII.2 the reparametrized curve y.t/ ´ x.t=/ is a periodic solution of
X
H
having period
0<jjT L
0
:
(2) We next consider a sequence ˛
j
& ˛
. By the above construction we find for
every j a periodic solution x
j
.t/ of the vector field X
H
having period 0<T
j
<L
0
on an energy surface S
j
or S
j
for a parameter
j
2 .˛
;˛
j
/. Therefore, we
find a subsequence converging to ˛
or to ˛
. In view of Proposition VIII.3 there
exists on S
˛
or on S
˛
a non-constant periodic solution and we have proved that
˛
2 ƒ or ˛
2 ƒ, as claimed in the lemma.
The function ˛ 7! c
0
.U
˛
/ 2 R is an increasing function on the interval I D
."; "/, because c
0
is a capacity and U
˛
U
˛
0
for ˛ ˛
0
. Therefore, in view
of a well-known theorem due to Lebesgue, the function is differentiable almost
everywhere and thus satisfies the assumptions of Lemma VIII.5 almost everywhere.

VIII.2. Hypersurfaces of contact type 317
From the lemma we conclude for the Lebesgue measure that
./m
˚
0 <"j 2 ƒ or 2 ƒ
D " D
m.I /
2
:
It remains to show that m.ƒ/ D m.I /. Arguing indirectly, we first assume that
m.I nƒ/>0. Then there exists for every small ı>0an interval J I satisfying
m.J \ .I n ƒ// .1 ı/m.J /. Now, for the interval J we can argue as we did
before for the interval I and find analogous to ./ the estimate
m.J \ ƒ/
m.J /
2
and choosing ı>0sufficiently small we arrive at the contradiction
m.J / D m.J \ .I n ƒ// C m.J \ƒ/ .1 ı C 1=2/m.J / > m.J /
which proves Theorem VIII.4.
We again point out that in the special situation of compact hypersurfaces S in
the symplectic standard space .R
2n
;!
0
/, the above requirement on the capacity c
0
is always fulfilled. For a direct proof in this case we refer to M. Struwe in [112]
It should be emphasized that not every compact regular energy surface admits
a periodic orbit. Examples of hypersurfaces that do not carry periodic orbits are
due to V. Ginzburg and M. Herman in the dimensions 2n 6 and we refer to the
survey article [40] by V. Ginzburg. The situation in dimension 2n D 4 is not yet
understood. V. Ginzburg and B. Gürel constructed in [43] a compact regular energy
surface of class C
2
in .R
4
;!
0
/ that does not carry a periodic orbit.
In his celebrated non-closing lemma, M. Herman constructs a smooth Hamil-
tonian function H
0
on a 4-dimensional symplectic manifold possessing a compact
regular energy surface S
0
for which in the open neighborhood
U D
[
2I
S
none of the energy surfaces S
admits a periodic solution and such that, moreover,
the same holds true for all Hamiltonian functions H that are close to H
0
in the
C
4
-topology. The example of M. Herman can be found in [52].
VIII.2 Hypersurfaces of contact type
We have seen that every compact and regular energy surface S contained in a
symplectic manifold .M; !/ gives rise to an abundance of periodic solutions, if
only a neighborhood of S has a finite capacity c
0
. These solutions are all near but
not necessarily on S. To guarantee periodic solutions on the surface S itself one

318 Chapter VIII. Applications of the capacity c
0
in Hamiltonian systems
needs additional conditions on the hypersurface S. Prompted by the early existence
results on convex and starlike hypersurfaces in .R
2n
;!
0
/, A Weinstein formulated
in [117] his seminal conjecture that a contact type hypersurface always carries a
periodic orbit.
Definition. A compact hypersurface S .M; !/ is of contact type, if, in a neigh-
borhood U M of S, there exists a vector field X possessing the following
properties.
(i) X is transversal to S, that is, X.x/ … T
x
S for all x 2 S.
(ii) L
X
! D ! on U .
The condition (ii) is equivalent to the requirement
.'
t
/
! D e
t
! on U
for the flow '
t
of the vector field X. Another (equivalent) definition of contact-
type will be formulated later on in Proposition VIII.8.
0
X
S
Figure VIII.6. A starlike compact hypersurface S R
2n
as an example of a hypersurface
of contact type.
Examples. (1) We assume S .R
2n
;!
0
/ to be a starlike compact hypersurface.
This requires the existence of an interior point which we may assume to be x
D 0,
having the property that every ray issuing from the point x
intersects the surface
S in exactly one point and does so transversally. Then, S is of contact type with
respect to the symplectic structure !
0
, since the vector field
X.x/ ´
1
2
x
is transversal to S and its flow '
t
is equal to
'
t
.x/ D e
t=2
x
so that .'
t
/
!
0
D .e
t=2
/
2
!
0
D e
t
!
0
for all t 2 R.
VIII.2. Hypersurfaces of contact type 319
(2) In particular, every strictly convex hypersurface S .R
2n
;!
0
/ is of contact
type. By this we refer to the smooth boundary of a strictly convex (bounded) set.
An example is the sphere S
2n1
R
2n
.
If S is a hypersurface of contact type in the symplectic manifold .M; !/, then
there exists a distinguished 1-parameter family of hypersurfaces S
, which forms
an open neighborhood U of S D S
0
by
U D
[
jj<"
S
:
This family is defined by the flow of the vector field X in the following way. Since
X is transversal to S , its flow '
t
induces for a small ">0a diffeomorphism
W S ."; "/ ! U onto a neighborhood U of S defined by
.x; / 7! '
.x/ D .x; /;
and we set
S
´ '
.S/
for jj <". Since S is of contact type, this diffeomorphism is very special.Ifx 2 S
and if 0 ¤ 2 L
S
.x/ is an element of the canonical line through the point x, then
it follows for all tangent vectors 2 T
x
S that
0 D e
t
!.; /
D .'
t
/
!.; /
D !
d'
t
.x/; d'
t
.x/
:
Because d'
t
.x/ is an isomorphism T
x
S ! T
'
t
.x/
S
t
between the tangent spaces,
it follows that
d'
t
.x/ 2 L
S
t
.'
t
.x//
so that
d'
t
W L
S
! L
S
t
induces a (vector bundle-) isomorphism between the canonical line bundles. Thus
we obtain a bijection between the characteristics of S and of S
t
. In particular, if
S
t
is a closed characteristic of the canonical line bundle L
S
t
, then the closed
curve
.'
t
/
1
./ S
is a closed characteristic of L
S
. From Theorem VIII.2 we now easily arrive at the
following statement.
Theorem VIII.6 (Hofer–Zehnder). If S .M; !/ is a compact hypersurface of
contact type and if for an open neighborhood U M of S the capacity c
0
.U; !/
is finite, then S possesses a closed characteristic.

320 Chapter VIII. Applications of the capacity c
0
in Hamiltonian systems
Proof. We take the diffeomorphism W S ."; "/ ! U introduced above and
satisfying S
t
D '
t
.S/ D .S; t/, and define the Hamiltonian function H W U ! R
by
H.'
t
.x// ´ t; x 2 S:
This Hamiltonian function has the compact energy surfaces S
t
Dfx 2 U j H.x/ D
tg for t<j"j which are regular. Indeed, differentiating in t we obtain
1 D dH.'
t
.x//
d
dt
'
t
.x/ D dH.'
t
.x// X.'
t
.x//
so that dH.'
t
.x// ¤ 0 for all '
t
.x/ 2 S
t
. In view of Theorem VIII.2 we find
a parameter value jt
j <", for which the energy surface S
t
carries a closed
characteristic and therefore also S D S
0
carries a closed characteristic.
A compact hypersurface in the symplectic standard space .R
2n
;!
0
/ always
possesses a bounded neighborhood of finite capacity c
0
and we deduce from The-
orem VIII.8 the celebrated solution of A. Weinstein’s conjecture due to C. Viterbo
[114] in 1987.
CorollaryVIII.7 (Viterbo). Every compact hypersurface S .R
2n
;!
0
/ of contact
type carries a closed characteristic.
In particular, convex and starlike hypersurfaces in .R
2n
;!
0
/ always carry a
periodic orbit and we have confirmed the pioneering results due to A. Weinstein
[116] and P. Rabinowitz [90] in 1978, resp. in 1979, which mark the beginning of
the investigation of global periodic phenomena of Hamiltonian systems in higher
dimensions.
We conclude this section by a useful characterization of hypersurfaces of contact
type which is frequently used as a definition of contact type.
Proposition VIII.8. A compact hypersurface S .M; !/ is of contact type if and
only if S is orientable and if there exists a 1-form ˛ on S satisfying
(i) d˛ D j
!,
(ii) ˛./ ¤ 0 for all 0 ¤ 2 L
S
,
where j W S ! M denotes the inclusion map and L
S
is the canonical line bundle
of S .
Proof. (1) We assume that S is of contact type and let X be the transversal vector
field in the neighborhood U S satisfying L
X
! D !. Since X is transversal, the
hypersurface S is orientable. We introduce the 1-form ˛ on U by
˛ ´ i
X
!:
Using Cartan’s formula and d! D 0 it follows that
! D L
X
! D d.i
X
!/ D d˛:
