Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

VIII.2. Hypersurfaces of contact type 321

We choose a vector 0 ¤  2 L

.x/, then !.v;/ D 0 for all v 2 T

S. Since !

is nondegenerate, !.v; / ¤ 0 for v 2 T

M n T

S. Therefore, we conclude from

the transversality of the vector ﬁeld X that

0 ¤ !.X.x/; / D .i

!/./ D ˛./; 0 ¤  2 L

.x/;

and we have veriﬁed the properties (i) and (ii) for the 1-form ˛.

(2) Conversely, let ˛ be the 1-form satisfying the properties (i) and (ii) in the

proposition. We shall extend this form onto a neighborhood U of S by the following

lemma.

Lemma VIII.9. There exists a 1-form  on a neighborhood U  S, which satisﬁes

d D ! on U and j



 D ˛ on S;

where j W S ! U is the inclusion mapping.

Postponing the proof of the lemma, we ﬁrst complete the proof of Proposi-

tion VIII.10. We deﬁne the vector ﬁeld X on U by i

! D , and obtain by Cartan’s

formula,

! D d D d.i

!/ D L

In view of property (ii),

0 ¤ ˛./ D ./ D .i

!/./ D !.X.x/; /; 0 ¤  2 L

.x/;

and using the deﬁnition of L

.x/ it follows that X.x/ … T

S. With the exception

of the lemma, the proposition is proved. 

Proof of the lemma. Because S is orientable and of codimension 1, there exists

a transversal vector ﬁeld Y in a neighborhood of S. Similarly to the gradient

ﬂow in Proposition VIII.1 the ﬂow of this vector ﬁeld deﬁnes a diffeomorphism

W S  ."; "/ ! U onto an open neighborhood U of S , for a small ">0.

The diffeomorphism satisﬁes .x; 0/ D x for all x 2 S . Using the projection

 W S  ."; "/ ! S, given by .x; t/ D x, we introduce the projection map

r D  B

1

W U ! S; .x; t/ 7! x;

which on S is the identity map. If we deﬁne the 1-form  on U by  D r



˛, then



 D .r Bj/



˛ D ˛. The 2-form ! d on U is closed, because ! is closed so

that

d.!  d/ D 0:

Moreover, it follows from (i) that



.!  d/ D d˛  d.j



/ D d˛  d˛ D 0:

322 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

Claim. We claim that there exists a 1-form # on U , which satisﬁes !  d D d#

and j



# D 0.

The claim completes the proof of the lemma as follows. We deﬁne the 1-form

 on U by  D  C # and obtain d D ! and j



 D j



 D ˛ as required in the

lemma and it remains to prove the claim.

Proof of the claim. The claim is a general fact about vector bundles which we apply

to the trivial bundle S R Š S ."; "/ which is diffeomorphic to U . We consider

the vector bundle p W E ! N over the manifold N and let ˛ be a k-form on E

satisfying d˛ D 0 and j



˛ D 0, where j W N ! E is the inclusion map (the zero

section of the bundle). We shall show that there exists a .k 1/-form ˇ on E which

satisﬁes ˛ D dˇ and ˇj

D j



ˇ D 0.

Indeed, since the ﬁbers are vector spaces we can deﬁne for t>0the map

W E ! E by '

.x/ D tx. This 1-parameter family of diffeomorphisms deﬁnes

the time dependent vector ﬁeld X

on E by

.x/ D X

.x// for t>0.In

view of d˛ D 0 it follows from Cartan’s formula that L

˛ D d.i

˛/ and so,



˛ D .'



˛ D d







Using j



˛ D 0 we obtain lim

s!0



˛ D p



˛ D 0 and since '

D Id

,we

conclude that

˛ D .'



˛  lim

s!0



D lim

s!0



˛dt







D d



˛dt



We deﬁne ˇ as the integral on the right, then ˇ is a .k 1/-form satisfying dˇ D ˛.

Moreover, if x 2 N , then X

.x/ D 0 and hence i

˛.x/ D 0 and so ˇ.x/ D 0,as

we wanted to prove. The proof of Proposition VIII.8 is complete. 

VIII.3 Examples from classical mechanics

We consider the standard symplectic space .R

/ equipped with the canonical

symplectic form !

, represented in the coordinates z D .x; y/ 2 R

 R

j D1

^ dx

VIII.3. Examples from classical mechanics 323

The Hamiltonian function H W R

! R deﬁnes the associated Hamiltonian vector

ﬁeld

.z/ D J rH.z/ D

H.z/



H.z/

;

denoted in physics as Pq D

H.q;p/ and Pp D

H.q;p/, using the coordinates

.q; p/ instead of .x; y/. Problems in physics often lead to Hamiltonian functions

of the type

H D kinetic energy C potential energy;

and are often of the form

H.x;y/ D

jyj

C V.x/;

with the potential function V W R

! R depending only on the variable x.A

somewhat more general classical Hamiltonian function takes the form

H.x;y/ D

hA.x/y; yiCV.x/;

where A.x/ is a positive deﬁnite symmetric matrix, so that the kinetic energy is a

Riemannian metric.

We shall show that for such Hamiltonian functions every compact regular energy

surface S Dfz 2 R

j H.z/ D Eg is of contact type. For this purpose we

formulate a criterion for energy surfaces in .R

/ to be of contact type, involving

the Liouville form  on R

deﬁned by

 D

iD1

Then d D

iD1

^ dx

D !

is the canonical symplectic form.

Theorem VIII.10. If a smooth function H W R

! R satisﬁes the inequality

.X

.x; y// > 0 for all .x; y/ 2 R

with y ¤ 0;

then every compact regular energy surface S Dfz 2 R

j H.z/ D Eg is of

contact type and hence carries a periodic solution.

Proof. We assume the energy surface S Dfz 2 R

j H.z/ D Eg to be compact

and regular, so that dH ¤ 0 on S and hence also X

¤ 0 on S and denote by

j W S ! R

the inclusion map. We make use of Proposition VIII.8 and distinguish

between two cases.

(1) We ﬁrst assume that S does not contain a point z D .x; 0/ where x 2 R

Then, by assumption, .X

/>0on S .If˛ ´ j



 is the Liouville form induced

324 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

on S , then (i) d˛ D j



d D j



and (ii) ˛.X

/ D .X

/>0, since X

a vector ﬁeld on S. Because 0 ¤ X

lies in the canonical line bundle L

which

is 1-dimensional, it follows that ˛./ ¤ 0 for all 0 ¤  2 L

. Consequently, the

energy surface S is of contact type in view of Proposition VIII.8.

(2) If S contains a point z D .x; 0/ where x 2 R

, then we modify the Liouville

form  near S and deﬁne for ">0the 1-form

˛ ´   "dF

where the function F W R

! R is deﬁned as

F.x;y/ ´



H.x; 0/; y



Clearly, d˛ D d D !

and the property (i), namely d.j



˛/ D j



on S,

follows. In order to apply Proposition VIII.8 to the 1-form j



˛, we still have to

show that

˛.X

/>0 on S

for a suitable ">0, so that the 1-form ˛ meets all the requirements in the deﬁnition

of contact type. Using the deﬁnition of  our assumption becomes

.X

/ D



H.x;y/;y



>0 if y ¤ 0:

On the other hand, .X

/ D 0 if y D 0. Consequently, for every ﬁxed x satisfying

.x; 0/ 2 S, the function y 7!h

H.x;y/;yi has in y D 0 a minimum, and thus

H.x;0/ D 0 for all .x; 0/ 2 S. By assumption dH D .

H/ ¤ 0 on S,

so that

H.x;0/ ¤ 0 if .x; 0/ 2 S:

By deﬁnition of the 1-form ˛,

˛.X

/ D .X

/ C "G

where G DdF .X

/ D



. Explicitly,

G.x; y/ D



.x; y/;

.x; 0/





j;kD1

.x; 0/

.x; y/y

At the points .x; 0/ 2 S,wehaveG.x; 0/ Dk

.x; 0/k

>0. Since S is

compact, it follows that G.x;y/>0at all the points .x; y/ 2 S where jyj <ıis

sufﬁciently small. Therefore, ˛.X

/>0at the points .x; y/ in S where jyj <ı

is small, since .X

/  0. This holds true for every ">0. Because S is compact

VIII.3. Examples from classical mechanics 325

and .X

/>0,ify ¤ 0, it follows that .X

/  c for a constant c>0, for all

.x; y/ in S satisfying jyjı for some small and positive ı. Finally, choosing "

small enough we achieve that ˛.X

/>0on S. As in step (1) it now follows that

S is of contact type. 

For the Hamiltonian vector ﬁeld X

.z/ D



H.z/;

H.z/



on R

obtain

.X

.x; y// D

j D1

H.x;y/ D



H.x;y/;y



If the function H is of the special form

H.x;y/ D

hA.x/y; yiCV.x/;

then

H.x;y/ D A.x/y. If the matrix A.x/ is positive deﬁnite, then

.X

/.x; y/ DhA.x/y; yi >0; y¤ 0

and we deduce from Theorem VIII.10 the following existence statement for systems

of classical mechanics.

Theorem VIII.11. If the Hamiltonian function H on the symplectic standard space

/ has the form

H.x;y/ D

hA.x/y; yiCV.x/

where A.x/ is positive deﬁnite, then every regular compact energy surface S D

fz 2 R

j H.z/ D Egis of contact type and, therefore, carries a periodic solution

of the Hamiltonian vector ﬁeld X

The phase space of a general system of classical mechanics is the cotangent

bundle  W T



N ! N over an n-dimensional manifold N , called a conﬁguration

space. As a set it is deﬁned as



N D

[

p2N



where .T



is the cotangent space, which is the vector space of linear forms

deﬁned on the tangent space T

N . The set T



N is equipped with a canonical man-

ifold structure deﬁned as follows. If .x

;:::;x

/ are the coordinates around the

point x in N ,a1-form ˛ 2 .T



is represented by ˛ D

j D1

having

the coordinates .y

;:::;y

/ and together .x

;:::;x

;:::;y

/ form local co-

ordinates in T



N . In these coordinates one can deﬁne the special 1-form  on T



./D

j D1

326 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

which so far has only a local meaning. It is remarkable that the above form  has a

global interpretation. In order to deﬁne a 1-form  on the manifold M D T



N we

have to deﬁne at every point P 2 M a linear form 

2 .T



which assigns to

every vector V 2 T

M a real number 

.V /. For the special 1-form this is done

as follows. If V 2 T

M then the point P 2 M D T



N is itself a linear form on

the tangent space T

N , where p D .P/ is the base point of P . Therefore, we

can evaluate the form P at the vector v ´ d

V 2 T

N where the projection

 W T



N ! N assigns to each P 2 T



N its base point p D .P/ in the manifold

N . Hence, d maps the tangent space T

M onto the tangent space T

N at the

point p and we can deﬁne

./

.V / ´ P.d

V/:

This canonically deﬁned 1-form is called the Liouville form on the manifold M D



N . It is sometimes called the tautological form on T



N , since it is deﬁned in

terms of itself. In the local coordinates introduced above the form ./ agrees with

the form ./. Locally we ﬁnd

d D

j D1

^ dx

;

from which we conclude that ! D d is a closed and nondegenerate 2-form on



N , hence a symplectic form. It is called the canonical symplectic structure on

the cotangent bundle T



N .

The Hamiltonian function of a classical mechanical system on the symplectic

manifold .T



N; d/ is again the sum of the kinetic and the potential energies. The

kinetic energy is given by a Riemannian metric on the conﬁguration space N which

deﬁnes a scalar product h; i

in every tangent space T

N . The Riemannian metric

induces a linear isomorphism T

N ! .T



at every point p deﬁned by the map

v 7!h;vi

and thus an isomorphism  W TN ! T



N between the tangent bundle

and the cotangent bundle of the manifold N . The induced Riemannian metric on



N is the push-forward h; iB

1

of the metric under the isomorphism ,

h; i





1

./; 

1

./

It deﬁnes the kinetic energy on the manifold M D T



N by

T./ Dh; i



The potential energy of the mechanical system is presented by a function V deﬁned

on the conﬁguration space N and, together with the kinetic energy, the Hamiltonian

system on the phase space T



N is deﬁned by the Hamiltonian function

H./ D T./C V ..//:

VIII.4. Poincaré’s continuation method 327

If .t/ is a solution of the Hamiltonian vector ﬁeld X

on T



N , the projection

x.t/ D ..t// describes the mechanical movement in the conﬁguration space.

Unfortunately little is known about the special capacity c

on cotangent bundles

except in the special case of the torus where c

is ﬁnite on open and bounded

sets. However, classical systems of the above form can be investigated by different

methods. We only mention that S.V. Bolotin [11] showed already in 1978 by

means of methods from Riemannian geometry that for a system whose Hamiltonian

function H W T



N ! R is of the form H./ D T./ C V..//, every compact

regular energy surface carries a periodic solution of X

VIII.4 Poincaré’s continuation method

In general, a periodic solution of a Hamiltonian vector ﬁeld is not isolated. It be-

longs to a 1-parameter family of periodic solutions parametrized by the energy and

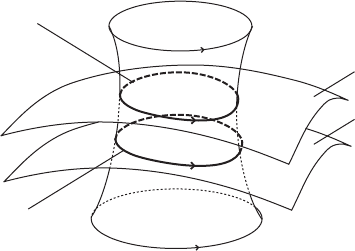
forming an embedded cylinder as illustrated in Figure VIII.7. This was already

known to H. Poincaré who designed perturbation methods for periodic orbits based

on the implicit function theorem. The method is local in nature and requires non-

degeneracy conditions on the Floquet multiplier of the given unperturbed reference

solution which are deﬁned as follows.

x.t;E/

x.t;E





Figure VIII.7. Embedded cylinder of periodic solutions x.t;E/ near the reference solution

x.t; E



Deﬁnition. If x.t/ is a non-constant periodic solution of the vector ﬁeld Px D X.x/

on the manifold M having period T>0and if '

is the ﬂow of X, then

.x.0// D x.T / D x.0/

and hence the linearized map at the point p D x.0/ is an endomorphism

.p/W T

M ! T

328 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

The eigenvalues of the linear map d'

.p/ are called Floquet multipliers of the

periodic solution x.t/ for the period T .

The signiﬁcance is the following. Looking for periodic solutions near x.t/, one

is tempted to solve the ﬁxed point problem '

.x/ D x resp. '

.x/  x D 0 for

x near p using the implicit function theorem. This leads to an investigation of the

linearized map at the reference solution,

.p/  1:

This map is singular, if there exists a Floquet multiplier equal to 1 which for

time independent vector ﬁelds is always the case!

Indeed, differentiating the ﬂow relation '

B '

.p/ D '

B '

.p/ in s at s D 0

one obtains

.p/ X.p/ D X.'

.p//

for all t.Ift D T is the period and hence '

.p/ D p, one ﬁnds

.p/ X.p/ D X.p/ 2 T

We have veriﬁed that 1 is a Floquet multiplier. If the vector ﬁeld X is the Hamil-

tonian vector ﬁeld X

on the symplectic manifold .M; !/, then the linearized map

.p/W



M; !.p/





M; !.p/



is symplectic and we conclude from Proposition V.5 that the multiplicity of the

Floquet multiplier 1 is at least 2. In the Hamiltonian case there always exist at least

two Floquet multipliers equal to 1!

Theorem VIII.12 (H. Poincaré). We consider the periodic solution x.t;E



/ of

the Hamiltonian vector ﬁeld X

on the symplectic manifold M having the energy

H.x.t// D E



and the period T



>0. If it possesses precisely two Floquet

multipliers equal to 1, then there exists a smooth 1-parameter family x.t; E/ of

solutions of periods T.E/ near T



on the energy surfaces S

Dfx 2 M j

H.x/ D Eg for E sufﬁciently close to E



. Under these conditions the solutions

x.t;E/ are unique and the periods depend smoothly on E.IfE ! E



, then, in

particular, T.E/ ! T.E



/ D T



Postponing the proof we observe that the reference solution x.t;E



/ is not

isolated in M as a periodic solution. The periodic solutions x.t;E/ correspond

to different values of the energy E and it turns out in the proof that, on the ﬁxed

energy surface E, the periodic solution is isolated among those periodic solutions

having periods close to T . Geometrically, the periodic solutions of the theorem ﬁll

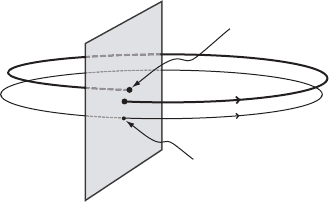
out an embedded cylinder in M as illustrated in Figure VIII.8.

It is useful to recall the construction of a transversal section map belonging to

a non-constant periodic solution x.t/ of a vector ﬁeld X on a manifold M having

VIII.4. Poincaré’s continuation method 329

p D .p/

.x/

†

x.t;E/

x.t;E



Figure VIII.8. The transversal map on † near p.

period T>0. We intersect the periodic solution x.t/ in the point p D x.0/ with

a transversal manifold †  M of codimension 1, so that

M D T

† ˚ spanfX.x/g

for all x 2 † near p. Such a manifold † is called a local transversal section of

x.t/ in the point p.

In view of the assumption, the ﬂow '

of X satisﬁes at time t D T ,

.p/ D p 2 †:

In a neighborhood U  † of p the ﬂow '

deﬁnes a smooth map

W U  † ! †;

in the following way. Given a point x 2 U  † near p D x.0/ we follow its

solution '

.x/, until, for the ﬁrst time, it meets † again at a time .x/>0, and we

deﬁne

.x/ D '

.x/

.x/ 2 †; x 2 U  †:

Since the vector ﬁeld X is transversal to the section †, the map x 7! .x/ 2 R is

a smooth map, deﬁned on † near the intersection point p and uniquely determined

by the conditions

.p/ D T;

.x/

.x/ 2 †; x 2 † \ U:

The map W † ! † which is deﬁned near the ﬁxed point p D .p/, is called a

transversal map or Poincaré map of the periodic solution x.t/. The eigenvalues of

its derivative

d .p/W T

†  T

M ! T

†  T

are related to the Floquet multipliers as follows.

330 Chapter VIII. Applications of the capacity c

in Hamiltonian systems

Proposition VIII.13. The derivative d'

.p/ has 1 as an eigenvalue associated

with the eigenvector X.p/. The other eigenvalues are the eigenvalues of d .p/.

The characteristic polynomials are related by

det.  d'

.p// D .  1/ det.  d .p//:

Proof. The ﬁrst statement we have already veriﬁed at the beginning of this section.

If  2 T

† is a tangent vector, then

d .p/ D d'

.p/ C

tDT

.p/ d .p/

D d'

.p/ C l./ X.p/;

where the linear form d .p/ 2 .T

†/



has been abbreviated by l so that d'

.p/ D

l./X.p/ C d .p/. With respect to the splitting

M D spanfX.x/g˚T

†;

we represent v 2 T

M by v D .˛X.p/; / for an ˛ 2 R and a tangent vector  in

†. Using d'

.p/X.p/ D X.p/ the linear map d'

has the representation

.p/ D

l

d .p/

with respect to the above splitting from which the proposition follows immediately.



In view of the construction of the local diffeomorphism of the section †,

the ﬁxed points of are the initial conditions of all periodic solutions near the

reference solution x.t/ which have periods near T



and we shall solve the ﬁxed

point equation .x/ D x near p in suitable coordinates.

Proof of Theorem VIII.12. If x.t/ is the non-constant reference solution of period



>0having energy E



, then dH.x/ ¤ 0 for all x 2 M near the orbit x.t/.Itis

convenient to introduce local coordinates x D .x

;:::;x

/ 2 R

locally around

p D x.0/ having the following properties.

(i) H.x

;:::;x

/ D x

;

(ii) p D .E



;0;:::;0/,

(iii) † Dfx j x

D 0g deﬁnes a local transversal section of x.t/.

To ﬁnd these coordinates, we ﬁrst choose the coordinates y D .y

;:::;y

/ 2 R