Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

27.4 Basic equations of the approximate stochastic dynamic method 691
The terms involving
˙
X
k
and ˙µ
k
can be eliminated with the help of (27.50) and
(27.66). This gives a fairly involved expression, which we are not going to state
explicitly. The interested reader may find this equation in explicit form in Epstein
(1969), Fortak (1973), or elsewhere.
Had we written out this equation, we would have found that new unknown
quantities appear in the form of the next higher moments τ
ij k
. Formally, we could
easily obtain a differential equation for τ
ij k
containing as new unknowns still higher
moments. We could go on indefinitely deriving prognostic equations for any order
of moments, but these would always contain the unknown next-higher generation
of moments. The same type of closure problem is already known from the theory
of turbulence. Since the deterministic prediction equations are nonlinear, it is
impossible to derive a closed finite set of prognostic equations for the moments. The
numerical evaluation of the third and even higher moments requires prohibitively
large amounts of computer time, so Epstein (1969) was compelled to close the
system of predictive equations consisting of the µ
k
and the σ
kl
by ignoring the
occurrence of the third-order moments τ
ij k
in the σ
kl
equations. Fleming (1971a)
discussed the closure problem very thoroughly. For details we refer to his paper.
Moreover, Fleming (1971a) also applied the stochastic dynamic method to in-
vestigate the effect of uncertainties in the initial conditions on the energetics of
the atmosphere. When one is investigating certain phenomena, the method makes
it possible also to study in a systematic fashion the uncertainties resulting from
the parameterization of neighboring scales. By introducing the quadratic ensem-
ble mean
µ
2
k
one may estimate the most probable energy distribution, which is
called the certain energy. With the help of the variance
σ
kk
or uncertainty, the
so-called uncertain energy can be determined. An atmospheric scale corresponding
to a certain wavenumber k becomes unpredictable whenever the uncertain energy
is as large as or even larger than the certain energy. For details we must refer to the
original literature.
We may easily recognize the advantages of the stochastic dynamic method over
the deterministic forecast. Stochastic dynamic forecasts produce a significantly
smaller mean square error than do deterministic forecasts. As discussed above,
the range of useful forecasts can be extended by applying the stochastic dynamic
method. The main disadvantage of this method is that forecasts require a much
higher level of computational effort than does the deterministic procedure.
Many research papers on the stochastic dynamic method have appeared in the
literature since Fortak (1973). The interested reader will have no difficulty in
finding the proper references. It is beyond the scope of this book to discuss newer
developments aiming to increase the accuracy of the forecast and the period of
useful predictability. Suffice it to say that, at present, even with the best available
weather-prediction models, the predictability on the synoptic scale hardly exceeds
692 Predictability
two weeks. A brief account of the predictability problem is also given by Pichler
(1997).
27.5 Problems
27.1: Show that equation (27.64) is valid.

Answers to problems
Chapter M1
M1.1: Yes.
M1.2: (a) linearly dependent, (c) linearly independent.
M1.3:
|
A
2
|
= 0.683
|
A
|
,α= 7.25
◦
M1.4:
(a) (A
1
,A
2
,A
3
) = (3, −2, 3), (b) (A
1
,A
2
,A
3
) = (7, 8, 8)
M1.8:
[
A,
B,
C] =
1
[A, B, C]
Chapter M2
M2.1:
=−
√
g
A
1
(q
2
q
3
− q
3
q
2
) + A
2
(q
3
q
1
− q
1
q
3
) + A
3
(q
1
q
2
− q
2
q
1
)
M2.4: The eigenvalues are
(λ
1
,λ
2
,λ
3
) = (2, 2 +
√
2, 2 −
√
2)
The corresponding eigenvectors are
A
1
= C
1
(i
1
− i
3
), A
2
= C
2
(i
1
−
√
2i
2
+ i
3
), A
3
= C
3
(i
1
+
√
2i
2
+ i
3
)
where the C
i
are constants.
693
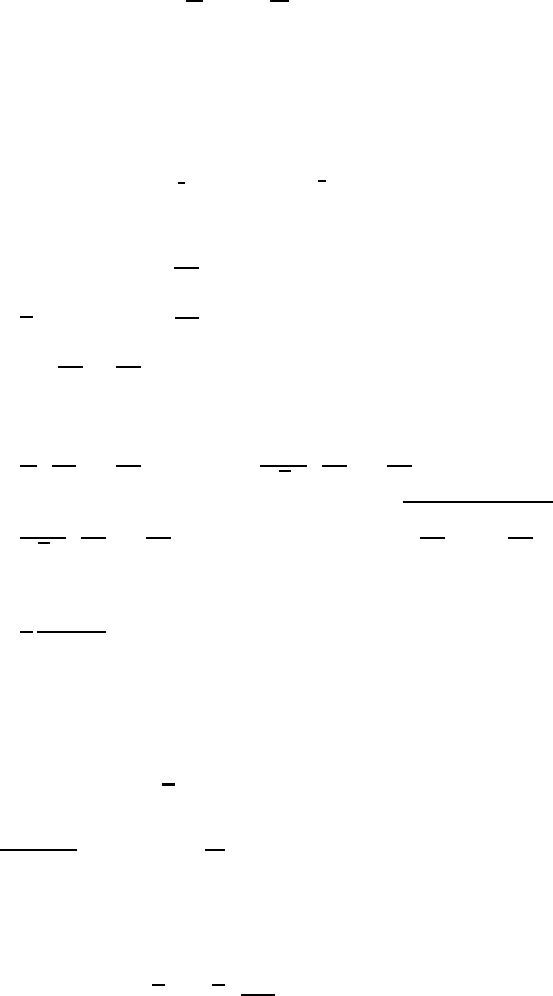
694 Answers to problems
Chapter M3
M3.2:
∇θ =
θ
T
∇T −
θ
∇
M3.3:
(a) 2Ω·r, (b) 2r × Ω, (c) 6Ω, (d) 2v·rΩ
M3.4:
(a) ∇
2
χ, (b) ∇
2
Ψ, (c) −∇ ×∇
2
Ψ +∇(∇
2
χ)
(d) ∇(∇
2
χ), (e) −
1
2
∇×(∇
2
Ψ) +
2
3
∇(∇
2
χ)
M3.6:
(b) (J
ij
) =
η
2
00
∂u
∂z
00
∂v
∂z
∂u
∂z
∂v
∂z
0
(c) λ
1
= 0,λ
2,3
=±ηA/2
(d) Ψ
1
=
1
A
∂v
∂z
i −
∂u
∂z
j
, Ψ
2
=
1
√
2A
∂u
∂z
i +
∂v
∂z
j + Ak
Ψ
3
=
1
√
2A
∂u
∂z
i +
∂v
∂z
j − Ak
with A =
∂u
∂z
2
+
∂v
∂z
2
(e) z =
1
x
r·
J·r
η∂u/∂z
Chapter M4
M4.1:
(a) g
11
= r
2
cos
2
ϕ, g
22
= r
2
,g
33
= 1,
g
ij
= 0ifi = j,
√
g
q
= r
2
cos ϕ
(b) g
11
=
1
r
2
cos
2
ϕ
,g
22
=
1
r
2
,g
33
= 1,g
ij
= 0ifi = j
M4.2:
W
q
1
= , W
q
2
= 0,W
q
3
= 0
M4.3:
√
g
ξ
=
√
g
q
∂q
3
∂ξ
q
1
,q
2
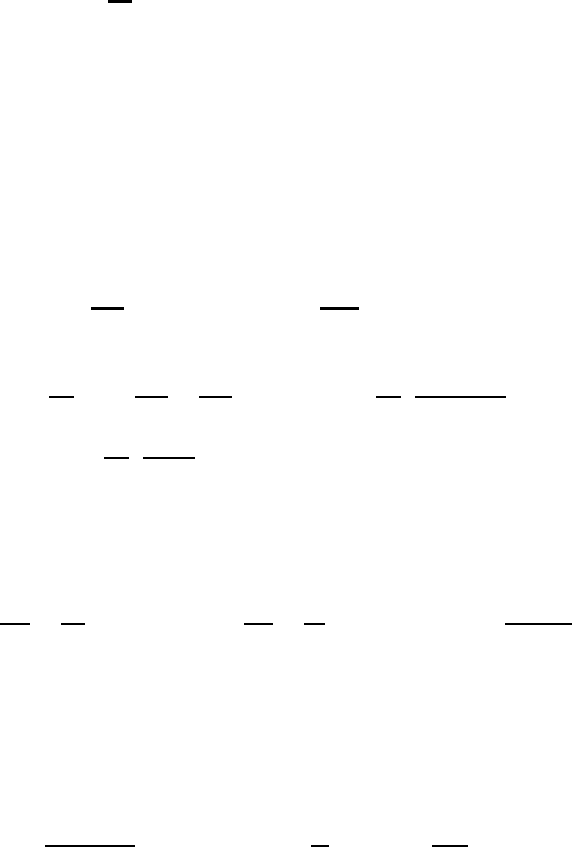
Answers to problems 695
Chapter M6
M6.4:
(a) k
L
0
A
y
(x,y = 0) + A
y
(x,y = M)
dx − k
×
M
0
A
x
(x = 0,y) + A
x
(x = L, y)
dy
(b) k
L
2
2
− 2 + cos M − sin M
M6.5:
(a) C[r(2) − r(1)], (b) 4Cπa
2
M6.6:
(a) 2πa
2
, (b) 2Ω ·
S
dS
Chapter 1
1.3:
(b) ∇·
J(v) = µ
∂
2
u
∂z
2
i =⇒ ∇ · J(v
1
) =−
µC
1
z
2
i, ∇·J(v
2
) = 0
1.4:
(b)
∂p
∂x
= µ
∂
2
u
∂y
2
+
∂
2
u
∂z
2
, (c) u =
∂p
∂x
R
2
− R
2
0
4µ
,
(d) Q =
∂p
∂x
πρR
4
0
8µ
Chapter 2
2.3:
M
λ
=
uw
a
−
uv
a
tan ϕ, M
ϕ
=
vw
a
+
u
2
a
tan ϕ, M
r
=−
u
2
+ v
2
a
Chapter 3
3.2: The flow is nonstationary since the time t appears explicitly.
(a) y = x,(b)x = y
1+ln y
.
3.3:
(a) y − y
0
=
C(x − x
0
)
(A + Bt
0
)
,(b)x − x
0
=
A
C
(y − y
0
) +
B
2C
2
(y − y
0
)
2

696 Answers to problems
Chapter 5
5.1:
∇·
J = µ[∇
2
v
A
+
1
3
∇(∇·v
A
)]
5.3:
(a) Parabolic velocity profile with
u(z) =
gρ sin α (2H − z)z
2µ
α is the angle of inclination.
(b) Isobars are parallel to the x-axis with p(z) = p
0
− gρ z cos α.
(c) The amount of fluid is
q =
gρ
2
H
3
sin α
3µ
(d)
H
0
ρ- dz =
ρ(gρ sin α)
2
H
3
3µ
5.4:
(a) u(z) = u(z = H )z/H .
(b) u(z) =
−
1
ρ
∂p
∂x
ρ(H − z)z
2µ
, parabolic flow, u
H
2
= u
max
5.5:
v
A
= Cr,C= constant =⇒ ∇ v
A
= C ∇r = CE, ∇·v
A
= 3C
D
ai
=
∇v
A
+ v
A
∇
2
−
∇·v
A
3
E = CE − CE = 0
J =
2µ
3
− λ
∇·v
A
E, p
2
(v
A
) = n · J = 3Cn
2µ
3
− λ
r ·
J · r = 3Cr
2
2µ
3
− λ
= 2F =±1
depending on the sign of C. The tensor ellipsoid is a spherical surface.
Chapter 6
6.1:
(a) (∇v)
I
=∇
2
φ, (∇v)
×
=∇
2
Ψ,
(∇v)
=
1
2
−∇(∇×Ψ) +∇×Ψ
∇
(b)
d
dt
(∇
2
Ψ) =−(∇
2
Ψ) ∇
2
φ − (∇
2
Ψ) ·∇(∇×Ψ)
+ (∇
2
Ψ) ·∇(∇φ) −∇
1
ρ
×∇p
Answers to problems 697
Chapter 7
7.1:
(a) v
r
=
∂χ
∂r
,v
t
=
1
r
∂χ
∂θ
(b)
∂
2
χ
∂r
2
+
1
r
∂χ
∂r
+
1
r
2
∂
2
χ
∂θ
2
= 0
7.2: χ
B
− χ
A
, where A and B are the endpoints of L.
7.3:
(a) χ = χ
A
1
+ 2nπ,wheren is an arbitrary integer.
(b) χ
B
2
= χ
A
2
= 0. Reason: After one complete circulation the angle θ returns
to its original value.
7.4:
(a)
|
v
h
|
=
a
2
+ b
2
,u= a, v = b
(b) ψ =−ay + bx = constant
Chapter 9
9.1:
ω
s
= ρ
s
∂φ
∂t
p
+ v
h
·∇
h,p
φ
s
− ρ
s
v
h
·∇
h,p
φ
s
In the case that at all times the earth’s surface is identical with the pressure surface
p
0
,wemayset∇
h,p
φ
s
=∇
h
φ
s
.
9.2:
tan α =
f
g
T
(2)
v
v
(1)
g
− T
(1)
v
v
(2)
g
T
(2)
v
− T
(1)
v
Chapter 12
12.1: In both cases you obtain 6[V (1)V (5) +V (2)V (4) +V (3)V (3) +V (4)V (2) +
V (5)V (1)].
Chapter 13
13.2:
=
∂
θ
∂z
H
ρc
p,0
−2/3
g
T
1/3
z
4/3

698 Answers to problems
13.3:
(a) - = κ
K
-
2/3
M
k
−5/3
,=
-(k)k
5/3
-
2/3
M
(b)
1
=
-(k)
ν
5/4
-
1/4
,
2
= k
ν
3
-
M
1/4
13.4:
(b) S
l
(0) = 1
13.5:
(13.84): S
l
= 0.143, (13.88): S
L
= 0.578
13.7:
u = u
g
1 −
√
2sinα
0
cos(Az + π/4 − α
0
)exp(−Az)
v = u
g
√
2sinα
0
sin(Az + π/4 − α
0
)exp(−Az)
z
g
=
3
4π
+ α
0
2k
f
Chapter 14
14.1: Reflection of U = U
0
sin(kx − ωt)onthex-axis.
14.2:
U = 2A sin
2πx
L
cos(ωt)
14.4: No. In order to obtain (14.37d) you must assume that α
0
= α
0
(z).
14.6:
H →∞, tanh(k
x
H ) → 1
14.7: The influence of the earth’s rotation is small.
14.8: 2200 m.
Chapter 15
15.5:
(a) From the plot it follows that the curvature changes sign. =⇒ Barotropic
instability.
(b ) −2 ≤ y
2
0
β/u
0
≤
2
3
.
Answers to problems 699
Chapter 16
16.1:
c = u
0
−
β
a
2
,a
2
= k
2
x
(1 + µ
2
), u = u
0
− Aa cos(ay + -)
Chapter 17
17.2:
ξ = ξ
0
+
f
0
2v
0
y
2
Chapter 18
18.3:
covariant:
d
dt
=
∂
∂t
+
v
1
r
2
cos
2
ϕ
∂
∂λ
+
v
2
r
2
∂
∂ϕ
+ v
3
∂
∂r
contravariant:
d
dt
=
∂
∂t
+
˙
λ
∂
∂λ
+ ˙ϕ
∂
∂ϕ
+ ˙r
∂
∂r
physical:
d
dt
=
∂
∂t
+
u
r cos ϕ
∂
∂λ
+
v
r
∂
∂ϕ
+ w
∂
∂r
18.4:
(a)
1
ρ
dρ
dt
+
1
r cos ϕ
∂u
∂λ
+
∂
∂ϕ
(v cos ϕ)
+
∂w
∂r
+
2w
r
= 0
(b)
1
ρ
dρ
dt
+
1
r cos ϕ
∂
∂λ
(r cos ϕ
˙
λ) +
∂
∂ϕ
(r ˙ϕ cos ϕ)
+
∂ ˙r
∂r
+
2 ˙r
r
= 0
18.5:
(a) W
1
= r
2
cos
2
ϕ, W
1
=
=
1
12
=−tan ϕ, =
1
13
=
1
r
,=
2
11
= cos ϕ sin ϕ
=
2
23
=
1
r
,=
3
11
=−r cos
2
ϕ, =
3
22
=−r
(b) ω
12
= r
2
cos ϕ sin ϕ, ω
13
=−r cos
2
ϕ,
ω
12
∗
= sin ϕ, ω
13
∗
=− cos ϕ
with =
k
ij
= =
k
ji
and ω
ij
=−ω
ji
. The remaining terms of W
i
,W
i
,ω
ij
,and=
k
ij
vanish.
700 Answers to problems
Chapter 19
19.4:
g
11
= -
2
cosh
2
r
cos
2
ϕ
,g
22
= g
33
= -
2
(cosh
2
r
−cos
2
ϕ
),g
ij
= 0,i= j
Chapter 20
20.3:
(a) For constant values of x,y,λ,andϕ the ratios ds
E,x
/d
sphere,λ
and ds
E,y
/d
sphere,ϕ
give the same result. Thus, the projection is conformal. m = 1/cos ϕ.
(b)
(dr)
2
=
1
m
2
(dx
2
+ dy
2
) + dz
2
K
A
=
1
2m
2
( ˙x
2
+ ˙y
2
) +
˙z
2
2
+
r
m
2
˙x +
r
2
m
2
g
11
= 1/m
2
,g
22
= 1/m
2
,g
33
= 1,g
ij
= 0,i= j
g
11
= m
2
,g
22
= m
2
,g
33
= 1,
√
g = 1/m
2
v
1
= ˙x/m
2
,v
2
= ˙y/m
2
,v
3
= ˙z
v
*
1
= ˙x/m, v
*
2
= ˙y/m, v
*
3
= ˙z
(c)
√
g
p
=−
1
m
2
gρ
Chapter 21
21.1:
dv
1
dt
−
v
2
n
g
nn
∂
∂x
(hg
nn
) −
fv
2
g
22
=−
1
ρ
∂p
∂x
+ gη
∂h
∂x
+
1
ρ
q
1
·∇ ·J
Chapter 22
22.3:
(a) The same as (22.58) but replace ∂M/∂x and ∂M/∂y as follows:
∂M
∂x
−→
∂N
∂x
+ ˙ρ
∂v
1
∂ρ
,
∂M
∂y
−→
∂N
∂y
+ ˙ρ
∂v
2
∂ρ
The hydrostatic equation is
∂N
∂ρ
=−
R
0
T
ρ
The individual derivative is
d
dt
=
∂
∂t
+ m
2
0
v
1
∂
∂x
+ v
2
∂
∂y
+ ˙ρ
∂
∂ρ
