Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

26.2 The basic equations 651
differential relation given by
∂
∂ϕ
= cos ϕ
∂
∂µ
(26.3)
Using the transformation (26.2), we find for the individual time derivative
d
dt
=
∂
∂t
+
U
a(1 − µ
2
)
∂
∂λ
+
V
a
∂
∂µ
+
˙
ξ
∂
∂ξ
(26.4)
We have discussed in an earlier chapter the fact that, due to ever-existing compu-
tational limitations and insufficient data to specify the initial conditions, the atmo-
sphere cannot be resolved to the extent necessary to include all scales of motion.
Therefore, it becomes necessary to average the pertinent atmospheric equations.
We know from our earlier work that the averaging process produces a number
of correlations but otherwise retains the form of the unaveraged equations. These
correlations represent the unresolved and, therefore, unknown subgrid fluxes which
need to be parameterized. Various research groups use different parameterizations
for the same correlations. Furthermore, these parameterizations are subject to revi-
sion as more and better observational data become available. For these reasons we
will not discuss the parameterizations in the present context. Instead, we assume
that the averaging process has been carried out already and we simply assign sym-
bols to the correlations. Moreover, to keep the notation simple we also leave out
the various averaging symbols.
Using (26.4) the equation for the U -component of the horizontal motion can
then be written as
∂U
∂t
+
U
a(1 − µ
2
)
∂U
∂λ
+
V
a
∂U
∂µ
+
˙
ξ
∂U
∂ξ
− fV
=−
1
aρ
∂p
∂λ
−
1
a
∂φ
∂λ
+ P
U
+ K
U
(26.5a)
The subgrid fluxes are simply denoted by P
U
and K
U
representing the vertical
change of the momentum flux and the tendency of U due to horizontal diffusion.
The description of the subgrid fluxes given here is rather vague but this has no effect
on the discussion of the spectral method. Similarly, we obtain for the V -component
∂V
∂t
+
U
a(1 − µ
2
)
∂V
∂λ
+
1
a
∂
∂µ
V
2
2
+
˙
ξ
∂V
∂ξ
+
U
2
+ V
2
a
µ
1 − µ
2
+ fU
=−
1 − µ
2
aρ
∂p
∂µ
−
1 − µ
2
a
∂φ
∂µ
+ P
V
+ K
V
(26.5b)
652 Modeling of atmospheric flow by spectral techniques
By omitting the P and K terms and reverting to the original variables u and v we
return to the original form of the horizontal equations of motion in the spherical
coordinate system.
Instead of transforming the U -andV -components directly, the motion will be
described in terms of the vorticity and divergence equations. This approach was
successfully practiced by Bourke (1972). To this end, first of all, we introduce the
vorticity into equation (26.5) by means of
ζ = e
r
·∇×v =
1
a cos ϕ
∂v
∂λ
−
∂
∂ϕ
(u cos ϕ)
=
1
a
1
1 − µ
2
∂V
∂λ
−
∂U
∂µ
(26.6)
After a few easy mathematical steps we obtain
∂U
∂t
− (f + ζ )V +
˙
ξ
∂U
∂ξ
+
R
0
T
v
a
∂ ln p
∂λ
+
1
a
∂
∂λ
(φ + E) = P
U
+ K
U
with E =
1
1 − µ
2
U
2
+ V
2
2
(26.7a)
∂V
∂t
+(f +ζ )U +
˙
ξ
∂V
∂ξ
+(1 −µ
2
)
R
0
T
v
a
∂ ln p
∂µ
+
1 − µ
2
a
∂
∂µ
(φ +E) = P
V
+K
V
(26.7b)
T
v
is the virtual temperature.
To formulate the prognostic equation of temperature we refer to equation (23.4).
We replace the individual derivative d/dt by means of (26.4) and use T
v
instead of
T in the second ω term and obtain
∂T
∂t
+
U
a(1 − µ
2
)
∂T
∂λ
+
V
a
∂T
∂µ
+
˙
ξ
∂T
∂ξ
−
R
0
T
v
c
p
p
ω = Q
h
(26.8a)
or
∂T
∂t
− F
T
= Q
h
with
F
T
=−
U
a(1 − µ
2
)
∂T
∂λ
−
V
a
∂T
∂µ
−
˙
ξ
∂T
∂ξ
+
R
0
T
v
c
p
p
ω
(26.8b)
The radiative flux divergence and the release of latent heat are thought to be included
in Q
h
. For the reason given in the introduction to this chapter we may write for the
moisture equation
∂q
∂t
+
U
a(1 − µ
2
)
∂q
∂λ
+
V
a
∂q
∂µ
+
˙
ξ
∂q
∂ξ
= Q
q
(26.9a)
or
∂q
∂t
− F
q
= Q
q
with F
q
=−
U
a(1 − µ
2
)
∂q
∂λ
−
V
a
∂q
∂µ
−
˙
ξ
∂q
∂ξ
(26.9b)
26.2 The basic equations 653
The continuity equation involving the generalized vertical coordinate ξ with the
scaling factor m
0
= 1 follows from (22.16) and is given by
∂
∂ξ
∂p
∂t
+∇
h
·
v
h
∂p
∂ξ
+
∂
∂ξ
˙
ξ
∂p
∂ξ
= 0(26.10)
Now, ∇
h
refers to spherical coordinates. Obviously, the hydrostatic equation in
terms of ξ is given by
∂φ
∂ξ
=−
R
0
T
v
p
∂p
∂ξ
(26.11)
Next, we wish to obtain a suitable expression for the generalized vertical velocity
ω = dp/dt. This is accomplished by rewriting (26.10),
∂
∂ξ
∂p
∂t
+ v
h
·∇
h
p +
˙
ξ
∂p
∂ξ
− v
h
·∇
h
p
+∇
h
·
v
h
∂p
∂ξ
= 0
or
∂
∂ξ
(ω − v
h
·∇
h
p) +∇
h
·
v
h
∂p
∂ξ
= 0
(26.12)
Integrating this expression between the limits shown yields
ξ
0
∂ω
∂ξ
dξ
=
ξ
0
∂
∂ξ
(v
h
·∇
h
p) dξ
−
ξ
0
∇
h
·
v
h
∂p
∂ξ
dξ
(26.13)
So far we have not specified the direction of ξ. The reason for this is that in the
expression
˙
ξ∂/∂ξ it does not make any difference whether ξ increases from the top
of the atmosphere or from the ground. If we start the integration from the ground
then (26.13) necessarily involves the evaluation of ω at the earth’s surface. Instead,
we let ξ increase in the downward direction from the top of the atmosphere to get
a simpler expression since ω(ξ = 0) = 0, or
ω(ξ) = (v
h
·∇
h
p)
ξ
−
ξ
0
∇
h
·
v
h
∂p
∂ξ
dξ
(26.14)
Since the surface pressure is not fixed in general but varies with time, we need
to derive a suitable expression for the surface-pressure tendency. By integrating
(26.10) we obtain
∂p
s
∂t
=−
1
0
∇
h
·
v
h
∂p
∂ξ
dξ or
∂ ln p
s
∂t
=−
1
p
s
1
0
∇
h
·
v
h
∂p
∂ξ
dξ
(26.15)
The predictive equations require knowledge of
˙
ξ. By integrating the continuity
equation (26.10) from the top of the atmosphere where p = 0 to the arbitrary level
ξ we find
˙
ξ
∂p
∂ξ
=−
∂p
∂t
ξ
−
ξ
0
∇
h
·
v
h
∂p
∂ξ
dξ
(26.16)
If ξ = 1 we again obtain equation (26.15).
654 Modeling of atmospheric flow by spectral techniques
We are now ready to derive the vorticity and the divergence equations in terms
of the transformed velocity variables U and V . To this end we apply the operators
a
−1
∂/∂µ to (26.7a) and [a(1 − µ
2
)]
−1
∂/∂λ to (26.7b) and subtract one of the
results from the other to obtain
1
a
∂
∂t
1
1 − µ
2
∂V
∂λ
−
∂U
∂µ
+
1
a(1 − µ
2
)
∂
∂λ
(f + ζ )U +
˙
ξ
∂V
∂ξ
+ (1 − µ
2
)
R
0
T
v
a
∂ ln p
∂µ
+
1
a
∂
∂µ
(f + ζ )V −
˙
ξ
∂U
∂ξ
−
R
0
T
v
a
∂ ln p
∂λ
=
1
a(1 − µ
2
)
×
∂P
V
∂λ
+
∂K
V
∂λ
−
1
a
∂P
U
∂µ
+
∂K
U
∂µ
(26.17)
The expressions in the square brackets which are differentiated with respect to λ
and µ will be abreviated by −F
V
and F
U
. Reference to equation (26.6), which is
the definition of the vorticity, shows that (26.17) can be written as
∂ζ
∂t
=
1
a(1 − µ
2
)
∂
∂λ
(F
V
+ P
V
) −
1
a
∂
∂µ
(F
U
+ P
U
) + K
ζ
with K
ζ
=
1
a
1
1 − µ
2
∂K
V
∂λ
−
∂K
U
∂µ
F
U
= (f + ζ )V −
˙
ξ
∂U
∂ξ
−
R
0
T
v
a
∂ ln p
∂λ
F
V
=−(f + ζ )U −
˙
ξ
∂V
∂ξ
− (1 − µ
2
)
R
0
T
v
a
∂ ln p
∂µ
(26.18)
Now we wish to introduce the horizontal divergence by means of
D =
1
a(1 − µ
2
)
∂U
∂λ
+
1
a
∂V
∂µ
(26.19)
The derivation of this equation will be left as an exercise. By applying the operators
[a(1 − µ
2
)]
−1
∂/∂λ to (26.7a) and a
−1
∂/∂µ to (26.7b) and then adding the results
we obtain
1
a
∂
∂t
1
1 − µ
2
∂U
∂λ
+
∂V
∂µ
−
1
a(1 − µ
2
)
∂
∂λ
(f + ζ )V −
˙
ξ
∂U
∂ξ
− R
0
T
v
∂ ln p
∂λ
+
1
a
∂
∂λ
(φ + E)
+
1
a
∂
∂µ
(f + ζ )U +
˙
ξ
∂V
∂ξ
+ (1 − µ
2
)
R
0
T
v
a
∂ ln p
∂µ
+
1 − µ
2
a
∂
∂µ
(φ + E)
=
1
a(1 − µ
2
)
∂
∂λ
(P
U
+ K
U
) +
1
a
∂
∂µ
(P
V
+ K
V
)
(26.20)
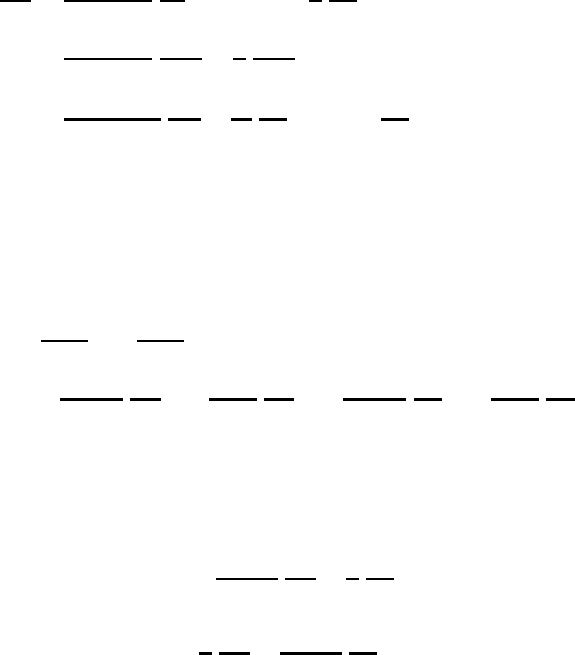
26.3 Horizontal discretization 655
On introducing the divergence according to (26.19) we find
∂D
∂t
=
1
a(1 − µ
2
)
∂
∂λ
(F
U
+ P
U
) +
1
a
∂
∂µ
(F
V
+ P
V
) + K
D
−∇
2
h
G
with K
D
=
1
a(1 − µ
2
)
∂K
U
∂λ
+
1
a
∂K
V
∂µ
,G= φ + E
∇
2
h
=
1
a
2
(1 − µ
2
)
∂
2
∂λ
2
+
1
a
2
∂
∂µ
(1 − µ
2
)
∂
∂µ
(26.21)
We now recall that, according to Helmholtz’s theorem (Section 6.1); the velocity
vector v can be decomposed into the sum of the rotational and the divergent parts,
v = v
ROT
+ v
DIV
. In the two-dimensional situation we may write, see equation
(6.12a),
ue
λ
+ ve
ϕ
=
U
cos ϕ
e
λ
+
V
cos ϕ
e
ϕ
= e
r
×∇
h
ψ +∇
h
χ
= e
ϕ
1
a cos ϕ
∂ψ
∂λ
− e
λ
cos ϕ
a
∂ψ
∂µ
+ e
λ
1
a cos ϕ
∂χ
∂λ
+ e
ϕ
cos ϕ
a
∂χ
∂µ
(26.22)
where ψ is the stream function and χ the velocity potential. Successive scalar
multiplication by the unit vectors e
λ
and e
ϕ
gives
(a) U =−
1 − µ
2
a
∂ψ
∂µ
+
1
a
∂χ
∂λ
(b) V =
1
a
∂ψ
∂λ
+
1 − µ
2
a
∂χ
∂µ
(26.23)
Using the horizontal Laplacian as shown in equation (26.21) leads to the well-
known expressions for the vorticity ζ and the divergence D as in (6.13):
ζ =∇
2
h
ψ, D =∇
2
h
χ (26.24)
The Laplacian in spherical ccordinates is defined in (26.21).
26.3 Horizontal discretization
The prognostic equations are formulated in terms of the vorticity ζ (26.18), the
divergence D (26.21), the temperature T (26.8), the moisture q (26.9), and the
surface pressure ln p
s
(26.15). These quantities as well as the surface geopoten-
tial φ will be represented in terms of the spherical functions. Before proceeding, we
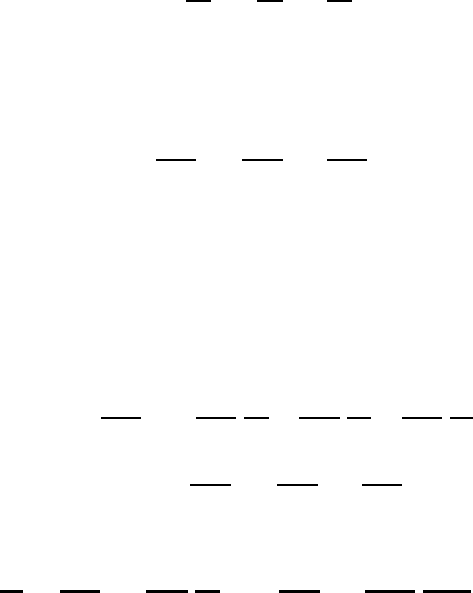
656 Modeling of atmospheric flow by spectral techniques
will briefly review those properties of the spherical functions which are needed in
our work. More detailed information can be found in any standard textbook on this
subject. We refer to Lense (1950).
26.3.1 Surface spherical harmonics
A function f (x, y,z) is said to be homogeneous of degree n if the following relation
holds:
f (λx, λy, λz) = λ
n
f (x,y, z)(26.25)
It is required that n is a real number, not necessarily an integer. Partial differentiation
of this identity with repect to λ, afterwards setting λ = 1, gives Euler’s relation
x
∂f
∂x
+ y
∂f
∂y
+ z
∂f
∂z
= nf (26.26)
A spherical function W
n
of degree n is defined to be a homogeneous potential
function of degree n. Solutions of Laplace’s equation, in general, are called potential
or harmonic functions. Therefore, the function W
n
satisfies the Euler relation
x
∂W
n
∂x
+ y
∂W
n
∂y
+ z
∂W
n
∂z
= nW
n
(26.27)
and the Laplace equation
∇
2
W
n
= 0(26.28)
Introduction of the spherical coordinates
x = r sin θ cos λ, y = r sin θ sin λ, z = r cos θ (26.29)
into the expression r∂W
n
(x,y, z)/∂r gives
r
∂W
n
∂r
= r
∂W
n
∂x
∂x
∂r
+
∂W
n
∂y
∂y
∂r
+
∂W
n
∂z
∂z
∂r
= x
∂W
n
∂x
+ y
∂W
n
∂y
+ z
∂W
n
∂z
= nW
n
(26.30)
Laplace’s equation in spherical coordinates is given by
∂
∂r
r
2
∂W
n
∂r
+
1
sin θ
∂
∂θ
sin θ
∂W
n
∂θ
+
1
sin
2
θ
∂
2
W
n
∂λ
2
= 0(26.31)
Since W
n
is homogeneous of degree n, we may write
W
n
(x,y, z) = W
n
(r sin θ cos λ, r sin θ sin λ, r cos θ)
= r
n
W
n
(sin θ cos λ, sin θ sin λ, cos θ)
= r
n
Y
n
(λ, θ)
(26.32)

26.3 Horizontal discretization 657
The part depending only on the angular coordinates (λ, θ) is known as the spherical
function Y
n
.
In order to find a solution for Y
n
, we first use (26.30) to obtain
r
2
∂W
n
∂r
= nrW
n
(26.33)
and
∂
∂r
r
2
∂W
n
∂r
= n(n + 1)W
n
(26.34)
so that (26.31) can be written as
1
sin θ
∂
∂θ
sin θ
∂Y
n
∂θ
+
1
sin
2
θ
∂
2
Y
n
∂λ
2
+ n(n + 1)Y
n
= 0(26.35)
If the function Y
n
(λ, θ) depends on θ only, we will call this function P
n
(θ), which
is known as the zonal spherical function. Thus the partial differential equation
(26.35) reduces to
1
sin θ
d
dθ
sin θ
∂P
n
(θ)
∂θ
+ n(n + 1)P
n
(θ) = 0(26.36)
Since θ is the only independent variable, we have obtained an ordinary differential
equation. On introducing the definition µ = cos θ, equation (26.36) assumes the
form
(1 − µ
2
)
d
2
P
n
(µ)
dµ
2
− 2µ
dP
n
(µ)
dµ
+ n(n + 1)P
n
(µ) = 0
(26.37)
which is known as Legendre’s differential equation. The particular solution
P
n
(µ) =
1
2
n
n!
d
n
dµ
n
(µ
2
− 1)
n
, −1 ≤ µ ≤ 1
(26.38)
is called the Legendre polynomial of degree n. It is well known that these polyno-
mials form a system of orthogonal functions on the interval −1 ≤ µ ≤ 1. Tables
of P
n
(µ) can be found in many textbooks and mathematical handbooks.
By differentiating (26.37) m times with respect to µ, we easily find
(1 − µ
2
)
d
2
P
(m)
n
(µ)
dµ
2
−2(m +1)µ
dP
(m)
n
(µ)
dµ
+ [n(n + 1) − m(m +1)]P
(m)
n
(µ) = 0
(26.39)
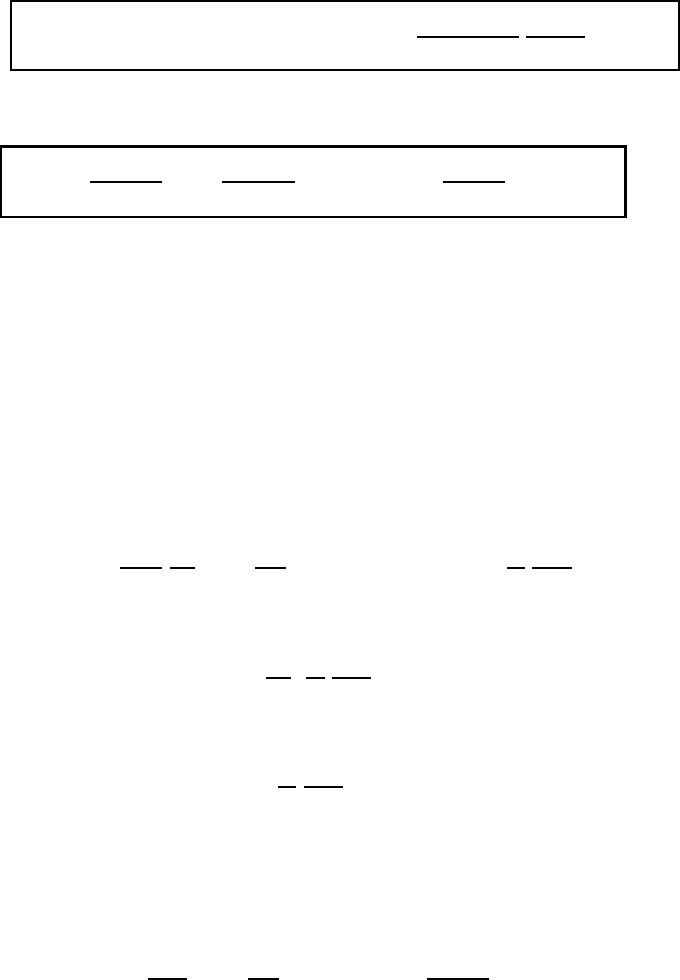
658 Modeling of atmospheric flow by spectral techniques
where m = 0, 1,... and P
(m)
n
(µ) represents the mth derivative of P
n
(µ). We leave
the verification of (26.39) to the exercises. We now introduce the definition
P
m
n
(µ) = (−1)
m
(1 − µ
2
)
m/2
P
(m)
n
(µ) = (−1)
m
(1 − µ
2
)
m/2
2
n
n!
d
n+m
dµ
n+m
(µ
2
− 1)
n
(26.40)
into (26.39) and obtain
(1 − µ
2
)
dP
m
n
(µ)
dµ
2
− 2µ
dP
m
n
(µ)
dµ
+
n(n + 1) −
m
2
1 − µ
2
P
m
n
(µ) = 0
(26.41)
which is known as the associated Legendre equation.TheP
m
n
(µ)aretheassociated
Legendre polynomials satisfying (26.41). Details regarding going from (26.39) to
(26.41) will be left to the problems. The associated Legendre polynomials also
form a system of orthogonal functions on the interval −1 ≤ µ ≤ 1. Some details
will be given shortly.
We will now obtain a suitable expression for the spherical surface function Y
n
,
also known as Laplace’s spherical function, by separating the variables θ and λ.
By substituting
Y
n
(λ, θ) = -(θ).(λ)(26.42)
into (26.35), we find
sin θ
-
d
dθ
sin θ
d-
dθ
+ n(n + 1) sin
2
θ =−
1
.
d
2
.
dλ
2
(26.43)
whose left-hand side depends on θ only, so we immediately obtain
d
dλ
1
.
d
2
.
dλ
2
= 0(26.44)
The solution to equation (26.41) is given by
1
.
d
2
.
dλ
2
=−m
2
(26.45)
where m is a constant. Moreover, the solution to (26.45) is
.(λ) = A
m
cos(mλ) + B
m
sin(mλ)(26.46)
By introducing µ = cos θ into (26.43) we obtain
(1 − µ
2
)
d
2
-
dµ
2
− 2µ
d-
dµ
+
n(n + 1) −
m
2
1 − µ
2
- = 0(26.47)
If m is an integer and 0 ≤ m ≤ n, the comparison of (26.47) with (26.41) shows

26.3 Horizontal discretization 659
that - is the associated Legendre polynomial P
m
n
(µ), i.e.
-(µ) = P
m
n
(µ)(26.48)
Since the differential equation (26.35) is linear and homogeneous, we obtain from
(26.42) the desired solution
Y
n
(λ, θ) =
n
m=0
[A
m
cos(mλ) + B
m
sin(mλ)]P
m
n
(cos θ)
(26.49)
We will now give the orthogonality relation for the assciated Legrende polyno-
mials:
+1
−1
P
m
n
(µ)P
m
l
(µ) dµ =
2
(2l + 1)
(l + m)!
(l − m)!
δ
n,l
(26.50)
As usual, the symbol δ
n,l
is the Kronecker delta. The proof of this relation is not
particularly difficult and can be found in any textbook on the subject. As will be
seen, the normalized form of the associated Legendre polynomials
P
m
n
(µ)isgiven
by
P
m
n
(µ) =
2n + 1
2
(n − m)!
(n + m)!
P
m
n
(µ)(26.51)
from which it follows that
+1
−1
P
m
n
(µ)
P
m
l
(µ) dµ = δ
n,l
(26.52)
Various useful identities involving the Legendre polynomials are listed next:
P
m
l
(µ) = 0ifm>l
P
m
l
(−µ) = (−1)
l+m
P
m
l
(µ)
P
−m
l
(µ) = (−1)
m
(l − m)!
(l + m)!
P
m
l
(µ)
P
−m
l
(µ) = (−1)
m
P
m
l
(µ)
P
m=0
l
(µ) = P
l
(µ)
(26.53)
The linearly independent parts of (26.49) are written down separately together
with the zeros of the function:
(a) Y
m
n
(λ, θ)
c
= cos(mλ) P
m
n
(cos θ) with zeros at λ =
π
2m
,
3π
2m
,...
(b) Y
m
n
(λ, θ)
s
= sin(mλ) P
m
n
(cos θ) with zeros at λ = 0,
π
m
,
2π
m
,...
(26.54)
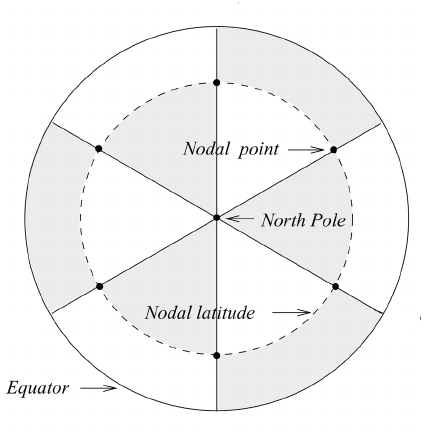
660 Modeling of atmospheric flow by spectral techniques
240
°
0
°
300
°
180
°
120
°
60
°
Fig. 26.1 Nodes of the surface harmonics Y
3
5
(λ, θ) = sin(3λ) P
3
5
(cos θ ). The function has
negative values in the shaded regions.
They are also known as the surface spherical harmonics of the first kind, tesseral
for m<nand sectoral for m = n. Their usefulness follows from the fact that
everywhere they are single-valued and continuous functions on the surface of the
sphere. The number of waves m around the latitude circle, defined either by (26.54a)
or by (26.54b), is known as the east–west planetary wavenumber. Moreover, the
function P
m
n
(µ)hasn − m zeros that are symmetric with respect to the equator
at θ = π/2. The number n − m is the so-called meridional wavenumber,which
is defined as the number of nodal zeros between the poles but excluding these. A
typical example for the tesseral harmonics is given in Figure 26.1 for n = 5and
m = 3. The so-called nodal latitude is 19.5
◦
. The nodal latitudes are also known
as the Gaussian latitudes. Values for other combinations of m and n are given by
Haurwitz (1940).
The alternating pattern of low and high values of variables may be thought of as
negative and positive deviations from the mean values. A specific and interesting
example involving the geopotential derived from the shallow-water equations is
given by Washington and Parkinson (1986).
Instead of using equation (26.49) in terms of cos(mϕ)andsin(mϕ)itismore
convenient to use the normalized form
