Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

24.2 The mathematical development of the two-level model 621
Utilizing this expression, the advection term of the first law of thermodynamics is
given by
v
g,2
·∇
h
(ψ
3
− ψ
1
) = v
g,1
·∇
h
(ψ
3
− ψ
1
) = v
g,3
·∇
h
(ψ
3
− ψ
1
)(24.6)
since the scalar triple product must vanish whenever two identical vectors appear.
This expression shows that the thermal wind is orthogonal to the gradient of the
relative topography:
(v
g,3
− v
g,1
)·∇
h
(ψ
3
− ψ
1
) = 0(24.7)
Our next task is to eliminate the generalized vertical velocity ω
2
in the predicitve
system (24.4). To accomplish this we multiply the heat equation by the term
λ
2
= f
2
0
/[σ
0
(p )
2
](24.8)
which is positive since
σ
0
is positive for large-scale motion. Furthermore, we use
the fact that, due to (24.6) in the advection term of the heat equation, v
g,2
may be
replaced by v
g,1
or v
g,3
. Therefore, (24.4c) can also be written as
∂
∂t
+ v
g,1
·∇
h
[λ
2
(ψ
3
− ψ
1
)] =−
f
0
ω
2
p
−
R
0
λ
2
c
p,0
f
0
d q
dt
2
∂
∂t
+ v
g,3
·∇
h
[λ
2
(ψ
3
− ψ
1
)] =−
f
0
ω
2
p
−
R
0
λ
2
c
p,0
f
0
d
q
dt
2
(24.9)
We observe that we have the same term on the right-hand sides of (24.4a) (24.4b)
and (24.9). Therefore, ω
2
can be eliminated by adding and subtracting the heat
equation (24.9) from (24.4a) and (24.4b), respectively. The result is
∂
∂t
+ v
g,1
·∇
h
[ζ
g,1
+ f − λ
2
(ψ
1
− ψ
3
)] = K
h
∇
2
h
ζ
g,1
−
R
0
λ
2
c
p,0
f
0
d q
dt
2
∂
∂t
+ v
g,3
·∇
h
[ζ
g,3
+ f + λ
2
(ψ
1
− ψ
3
)] = K
h
∇
2
h
ζ
g,3
+
R
0
λ
2
c
p,0
f
0
d q
dt
2
(24.10)
In order to have a concise notation we introduce the following definitions:
q
1
= ζ
g,1
− λ
2
(ψ
1
− ψ
3
) =∇
2
h
ψ
1
− λ
2
(ψ
1
− ψ
3
)
q
3
= ζ
g,3
+ λ
2
(ψ
1
− ψ
3
) =∇
2
h
ψ
3
+ λ
2
(ψ
1
− ψ
3
)
(24.11)
622 A two-level prognostic model, baroclinic instability
into (24.10). On momentarily setting K
h
and d q/dt equal to zero, the basic pre-
diction equations are given by
∂
∂t
+ v
g,1
·∇
h
(q
1
+ f ) = 0,
∂
∂t
+ v
g,3
·∇
h
(q
3
+ f ) = 0 (24.12)
This form is particularly suitable for demonstrating the principle of the numerical
integration procedure.
24.2.1 The principle of the numerical integration procedure
Step 1
Prescribe at the initial time t
0
the two independent variables ψ
1
(x,y, t
0
= 0) and
ψ
3
(x,y, t
0
= 0). Calculate v
g,1
= k ×∇
h
ψ
1
, v
g,3
= k ×∇
h
ψ
3
, and q
1
,q
3
.
Step 2
Compute the tendencies ∂q
1
/∂t, ∂q
3
/∂t and find q
1
,q
3
at t
1
= t
0
+ t by solving
(24.12) according to
q
1
(t
1
) = q
1
(t
0
) − t [v
g,1
·∇
h
(q
1
+ f )]
t
0
q
3
(t
1
) = q
3
(t
0
) − t [v
g,3
·∇
h
(q
3
+ f )]
t
0
(24.13)
Step 3
From q
1
,q
3
at time t
1
calculate ψ
1
,ψ
3
in order to iterate. We proceed by defining
the quantities
ψ
+
=
ψ
1
+ ψ
3
2
,ψ
−
=
ψ
1
− ψ
3
2
,q
+
=
q
1
+ q
3
2
,q
−
=
q
1
− q
3
2
(24.14)
Addition and subtraction of the two equations (24.11) yields
q
+
=
1
2
∇
2
h
(ψ
1
+ ψ
3
),q
−
=
1
2
∇
2
h
(ψ
1
− ψ
3
) − λ
2
(ψ
1
− ψ
3
)(24.15)
When they are stated in the form
∇
2
h
ψ
+
= q
+
, ∇
2
h
ψ
−
− 2λ
2
ψ
−
= q
−
(24.16)
we recognize that these two equations are decoupled. They represent two boundary-
value problems of the Poisson and Helmholtz type, which can be solved by well-
known numerical methods if suitable boundary conditions have been provided.
Step 4
From ψ
+
and ψ
−
we find ψ
1
= ψ
+
+ ψ
−
and ψ
3
= ψ
+
− ψ
−
. In order to iterate
we again start with step 1, where now t
0
is replaced by t
1
.

24.3 The Phillips quasi-geostrophic two-level circulation model 623
We would like to remark that the complete decoupling stated in (24.16) is
possible only for the two-level model, where by a three-dimensional problem
could be reduced to the solution of two-dimensional partial differential equations.
Each of these contains only one dependent variable. In multilevel models coupled
systems must be solved simultaneously.
The model expressed by the prediction equations (24.12) is a typical short-range-
forecast model. In order to extend the time interval of the forecast, we must also
include heat sources and large-scale diffusion.
24.3 The Phillips quasi-geostrophic two-level circulation model
We employ the basic predictive equations (24.9) but now we include the large-
scale diffusion and heating terms by taking K
h
= 0and(d q/dt)
2
= 0. We consider
channel flow with solid walls at the southerly and northerly boundaries of the model
as shown in Figure 24.2. For f we take the β approximation f = f
0
+ βy;the
large-scale exchange coefficient K
h
is assumed to be a constant. The heating term
(d
q/dt)
2
represents the sum of radiative heating (d q/dt)
2,rad
and of heat sources
resulting from turbulent heat fluxes (d
q/dt)
2,tur
. To represent the radiative effects
we assume that we have a heat source at y =−d/2andasinkaty = d/2 with a
linear variation between the walls:
d
q
dt
2,rad
=−
2y
d
Q
rad
,Q
rad
> 0(24.17)
The turbulent heat flux will be approximated with the help of (11.85):
J
θ
t
=−ρ c
p
K
h
∇
h
θ (24.18)
Since the heat equation applies to the level p
2
, we may replace the potential
temperature
θ by the actual temperature T
2
at this level and absorb the constant
2,rad
2,rad
Fig. 24.2 The geometry of the channel flow.

624 A two-level prognostic model, baroclinic instability
(p
0
/p
2
)
R
0
/c
p,0
into the large-scale turbulent exchange coefficient K
h
.However,itis
still open to debate whether cyclonic and anticyclonic activities may be viewed as
atmospheric macroturbulence so that large- and small-scale turbulent fluxes may
be treated analogously. The turbulent heat flux is approximated as
d
q
dt
2,tur
=−
1
ρ
∇
h
·J
θ
t
= c
p
K
h
∇
2
h
T
2
with T
2
=−
p
2
R
0
∂φ
∂p
2
=−
p
2
f
0
(ψ
3
− ψ
1
)
R
0
p
=
2f
0
ψ
−
R
0
(24.19)
Substitution of (24.17) and (24.19) together with the definitions (24.11) into (24.10)
yields the final form of the prediction equations:
∂
∂t
+ v
g,1
·∇
h
(q
1
+ βy) =
2λ
2
R
0
y
c
p,0
f
0
d
Q
rad
+ K
h
∇
2
h
q
1
∂
∂t
+ v
g,3
·∇
h
(q
3
+ βy) =−
2λ
2
R
0
y
c
p,0
f
0
d
Q
rad
+ K
h
∇
2
h
q
3
(24.20)
These equations may be integrated analogously to the procedure described above
by including the inhomogeneous terms which were left out of equations (24.12)
for simplicity.
Phillips (1956) used the system (24.20) to carry out the first successful
numerical experiment to simulate the general circulation. He added another term
to the second equation of (24.20). For details see the original paper.
24.4 Baroclinic instability
As stated in the introduction to this chapter, the solutions of baroclinic models may
become physically unstable when the baroclinicity, i.e. the vertical wind shear,
is sufficiently large and the static stability is sufficiently small. This instability
behavior is known as baroclinic instability and is common to all baroclinic models.
Baroclinic instability is responsible for the development of atmospheric cyclones
and anticyclones.
The analysis proceeds by linearizing the fundamental equations (24.12). The
stationary basic state and the disturbances are designated with an overbar and
primes, respectively. Application of the Bjerkness linearization rule immediately
results in the following system:
∂
∂t
+
v
g,1
·∇
h
q
1
+ v
g,1
·∇
h
(q
1
+ f ) = 0
∂
∂t
+
v
g,3
·∇
h
q
3
+ v
g,3
·∇
h
(q
3
+ f ) = 0
(24.21)
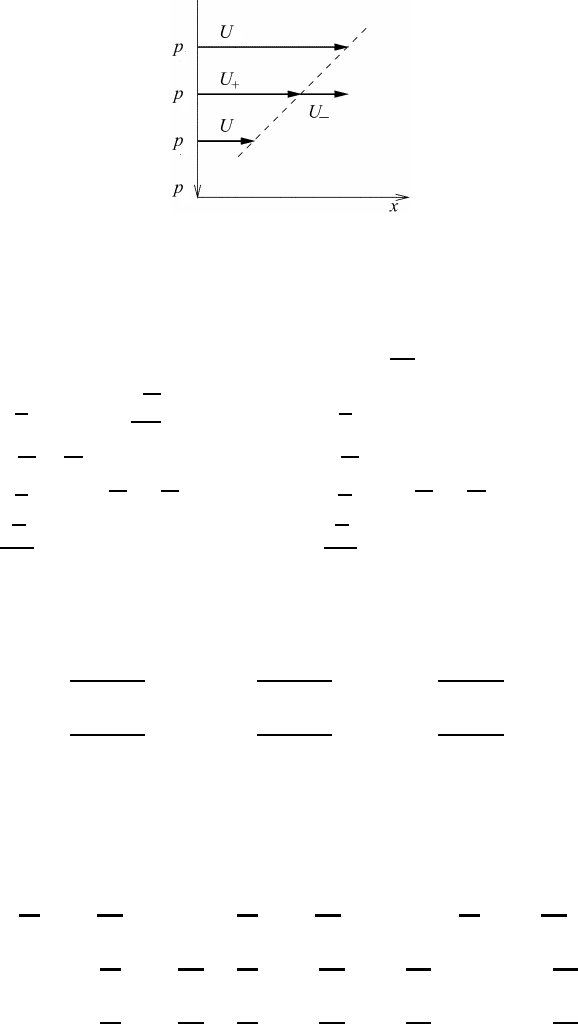
24.4 Baroclinic instability 625
1
1
2
3
3
4
Fig. 24.3 The vertical profile of the horizontal wind.
Next we must describe the basic state:
f = f
0
+ βy, β =
∂f
∂y
= constant
u
g
= U =−
∂
ψ
∂y
= constant,
v
g
= 0
ψ = ψ(y), ∇
2
h
ψ = 0
q
1
=−λ
2
(ψ
1
− ψ
3
), q
3
= λ
2
(ψ
1
− ψ
3
)
∂
q
1
∂y
= λ
2
(U
1
− U
3
),
∂q
3
∂y
=−λ
2
(U
1
− U
3
)
(24.22)
The mean values U
+
,ψ
+
,q
+
and the differences U
−
,ψ
−
,q
−
are defined as
U
+
=
U
1
+ U
3
2
,ψ
+
=
ψ
1
+ ψ
3
2
,q
+
=
q
1
+ q
3
2
U
−
=
U
1
− U
3
2
,ψ
−
=
ψ
1
− ψ
3
2
,q
−
=
q
1
− q
3
2
(24.23)
Figure 24.3 shows the vertical distribution of the horizontal wind and the
corresponding values of U
+
and U
−
. To facilitate the analysis we introduce the
Q operators by putting
Q
1
=
∂
∂t
+ U
1
∂
∂x
,Q
3
=
∂
∂t
+ U
3
∂
∂x
,Q
+
=
∂
∂t
+ U
+
∂
∂x
=⇒
Q
1
=
∂
∂t
+ U
1
∂
∂x
=
∂
∂t
+ U
+
∂
∂x
+ U
−
∂
∂x
= Q
+
+ U
−
∂
∂x
Q
3
=
∂
∂t
+ U
3
∂
∂x
=
∂
∂t
+ U
+
∂
∂x
− U
−
∂
∂x
= Q
+
− U
−
∂
∂x
(24.24)
By employing these definitions, the linearized fundamental equations (24.21) can
626 A two-level prognostic model, baroclinic instability
be written as
(a) Q
1
q
1
+
∂ψ
1
∂x
(2λ
2
U
−
+ β) = Q
+
q
1
+ U
−
∂q
1
∂x
+
∂ψ
1
∂x
(2λ
2
U
−
+ β) = 0
(b) Q
3
q
3
+
∂ψ
3
∂x
(−2λ
2
U
−
+ β) = Q
+
q
3
− U
−
∂q
3
∂x
+
∂ψ
3
∂x
(−2λ
2
U
−
+ β) = 0
(24.25)
In order to derive a suitable form for the solution of the predictive equations we
add and subtract (24.25a) and (24.25b) and find
Q
+
q
+
+ U
−
∂q
−
∂x
+ 2λ
2
U
−
∂ψ
−
∂x
+ β
∂ψ
+
∂x
= 0
Q
+
q
−
+ U
−
∂q
+
∂x
+ 2λ
2
U
−
∂ψ
+
∂x
+ β
∂ψ
−
∂x
= 0
(24.26)
Next we eliminate q
+
and q
−
by introducing the above definitions. Observing
(24.16), we obtain the expressions
q
+
=
q
1
+ q
3
2
=
1
2
∇
2
h
(ψ
1
+ ψ
3
) =∇
2
h
ψ
+
q
−
=
q
1
− q
3
2
=
1
2
∇
2
h
(ψ
1
− ψ
3
) − λ
2
(ψ
1
− ψ
3
) =∇
2
h
ψ
−
− 2λ
2
ψ
−
(24.27)
to be substituted into equation (24.26). This gives the final forms of the prognostic
equations:
Q
+
∇
2
h
+ β
∂
∂x
ψ
+
+ U
−
∂
∂x
∇
2
h
ψ
−
= 0
Q
+
∇
2
h
− 2λ
2
+ β
∂
∂x
ψ
−
+ U
−
∂
∂x
∇
2
h
+ 2λ
2
ψ
+
= 0
(24.28)
which are linear in ψ
+
and ψ
−
. In order to solve this system we use the trial
solutions
ψ
+
ψ
−
=
A
+
A
−
exp[ik
x
(x − ct)] (24.29)
where we assume that the perturbations depend on x and t only. The quantities A
+
and A
−
are constant amplitudes, k
x
= 2π/L
x
is the wavenumber in the x-direction
corresponding to the wavelength L
x
,andc is the phase velocity of the waves. From
(24.29) we easily obtain the operators
∂
∂t
=−ik
x
c,
∂
∂x
= ik
x
, ∇
2
h
=−k
2
x
=⇒
Q
+
=
∂
∂t
+ U
+
∂
∂x
=−ik
x
(c − U
+
)
(24.30)

24.4 Baroclinic instability 627
Using (24.30) in (24.28) yields the homogeneous system
(a)
(c − U
+
)k
2
x
+ β
A
+
− U
−
k
2
x
A
−
= 0
(b)
2λ
2
− k
2
x
U
−
A
+
+
(c − U
+
)
2λ
2
+ k
2
x
+ β
A
−
= 0
(24.31)
where we have canceled out the exponential term representing the form of the
wave. To find nontrivial solutions of this homogeneous system, i.e. A
+
= 0and
A
−
= 0, the determinant of the coefficient matrix must vanish:
(c − U
+
)k
2
x
+ β − U
−
k
2
x
2λ
2
− k
2
x
U
−
(c − U
+
)
2λ
2
+ k
2
x
+ β
= 0(24.32)
The expansion of this determinant results in the frequency equation
(c − U
+
)
2
+ 2(c − U
+
)
β
λ
2
+ k
2
x
k
2
x
2λ
2
+ k
2
x
+
β
2
+ U
2
−
k
2
x
2λ
2
− k
2
x
k
2
x
2λ
2
+ k
2
x
= 0(24.33)
for the determination of the phase velocity c. The solution of this quadratic equation
is
c
1,2
= U
+
−
β
λ
2
+ k
2
x
k
2
x
2λ
2
+ k
2
x
±
√
δ
with δ =
β
2
λ
4
k
4
x
2λ
2
+ k
2
x
2
− U
2
−
2λ
2
− k
2
x
2λ
2
+ k
2
x
(24.34)
Inspection of (24.34) shows that we have either two real roots (δ>0) or two
complex conjugated roots (δ<0), resulting in baroclinic stability or instability,
respectively.
24.4.1 The instability condition
For a fixed wavenumber k
x
= constant the two roots c
1,2
can now be used to
construct the solution to (24.28) as
ψ
+
ψ
−
=
A
+,1
A
−,1
exp[ik
x
(x − c
1
t)] +
A
+,2
A
−,2
exp[ik
x
(x − c
2
t)] (24.35)
We note that the amplitudes A
+
and A
−
are not independent. The relation between
A
+
and A
−
can be found from (24.31). We select (24.31a) and find the ratio
A
−,j
A
+,j
=
k
2
x
(c
j
− U
+
) + β
k
2
x
U
−
,j= 1, 2(24.36)

628 A two-level prognostic model, baroclinic instability
We could have also chosen (24.31b) to form the ratio, but the ratio is more
complicated. From matrix theory it is known that every eigenvalue has an infinite
number of eigenvectors. If X is an eigenvector then any scalar multiple of X is
also an eigenvector with the same eigenvalue. Therefore, we may write for the
components of the two eigenvectors in (24.35) the product
A
+,j
= B
j
ψ
+,j
,A
−,j
= B
j
ψ
−,j
,j= 1, 2(24.37)
where B
1
and B
2
are two arbitrary integration constants that may be determined
from general initial conditions. Thus, we may write the solution in the form
ψ
+
ψ
−
= B
1
ψ
+,1
ψ
−,1
exp[ik
x
(x − c
1
t)] + B
2
ψ
+,2
ψ
−,2
exp[ik
x
(x − c
2
t)]
(24.38)
By assigning the value 1 to one of the components, from (24.36) we obtain for the
second component
ψ
+,j
= 1,ψ
−,j
=
k
2
x
(c
j
− U
+
) + β
k
2
x
U
−
,j= 1, 2(24.39)
A particular example of the determination of an eigenvector was given in Section
4.2.2.
Suppose that the two roots c
1,2
are real. In this case the solution (24.38) is
bounded and the two partial waves move along the x-direction without change of
amplitude, i.e. without change of shape. If the roots are complex conjugate, one of
the two partial waves approaches infinity with increasing time so that the solution
is physically unstable.
Inspection of equation (24.34) shows that the sign of the discriminant
determines whether the solution is physically stable or unstable, or even neutral.
If δ>0 we have stability since c
1,2
are real quantities. If δ<0 we have instability
since c
1,2
are complex conjugate; δ = 0 denotes the neutral case.
24.4.2 Stable and unstable regions
Of special significance is the transition from the stable to the unstable region, which
is characterized by the condition δ = 0. By treating β as a constant, we may view
the equation
δ(U
−
,λ
2
,k
x
) = δ(U
−
, σ
0
,L
x
) = 0(24.40)
as a surface in space with the three coordinates U
−
, σ
0
= f
2
0
/[(p )
2
λ
2
], and L
x
=
2π/k
x
separating the stable from the unstable region. This surface is schematically
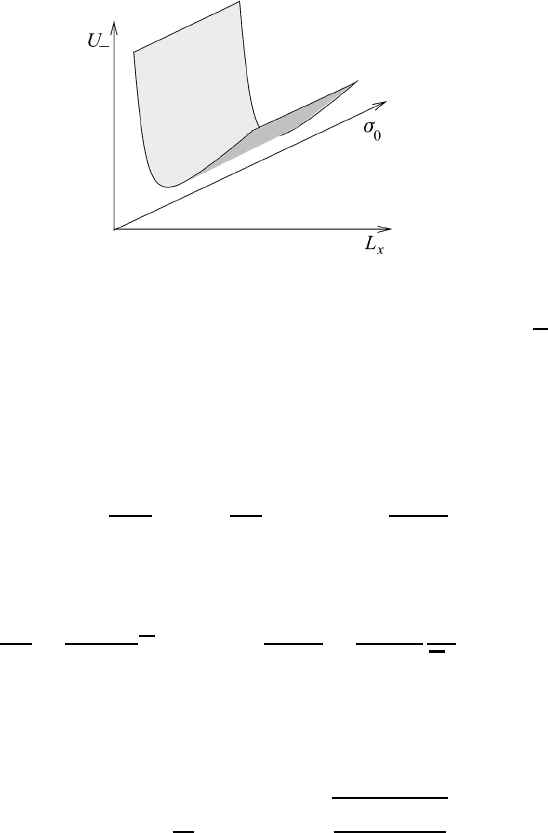
24.4 Baroclinic instability 629
Fig. 24.4 The neutral surface separating the stable from the unstable region.
shown in Figure 24.4. Thus, a particular choice of the coordinates (U
−
, σ
0
,L
x
)
determines whether the corresponding solution (24.38) is stable or unstable. The
separating surface is known as the neutral surface.
A convenient mathematical form of the neutral surface will be derived now. For
δ = 0 from (24.34) we find by obvious steps
k
4
x
4λ
4
− k
4
x
=
β
2
λ
4
U
2
−
=⇒
k
4
x
2λ
4
− 1
2
= 1 −
β
2
4U
2
−
λ
4
(24.41)
The latter equation motivates the introduction of the following (x,y)-coordinates:
x =
k
4
x
2λ
4
=
k
4
x
(p )
4
2f
4
0
σ
0
2
,y=
2U
−
λ
2
β
=
2f
2
0
(p )
2
β
U
−
σ
0
(24.42)
Therefore, the coordinate x gives the quantity k
4
x
in units of 2λ
4
while y expresses
the quantity U
−
in units of β/(2λ
2
). From (24.41) and (24.42) we obtain the equation
of the neutral surface:
(x − 1)
2
= 1 −
1
y
2
=⇒ y =±
1
1 − (x − 1)
2
(24.43)
whose graph is shown in Figure 24.5. Reflecting this curve on the x-axis gives the
representation of the neutral surface for negative values of y.Inthefollowingwe
will discuss positive y values only. Since according to (24.42) x ≥ 0, we recognize
that there is no need to consider negative x values.
From (24.43) we recognize that no real values of y exist for x>2andthat
the ordinate y approaches infinity for x = 0andx = 2. Furthermore, for x = 1
we find y = 1, which is the minimum value of the curve, as may be verified by
differentiation.
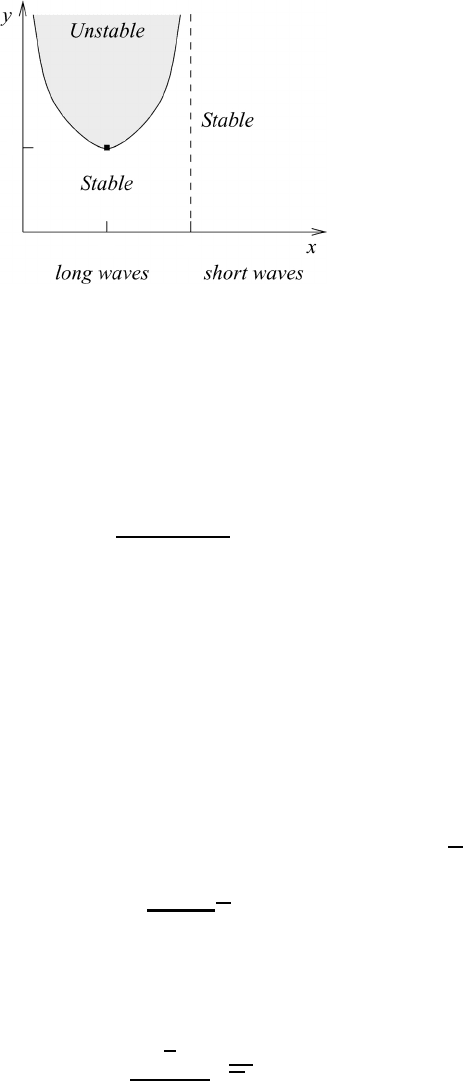
630 A two-level prognostic model, baroclinic instability
1
1
2
δ > 0
δ < 0
Fig. 24.5 A schematic representation of the stable (δ>0) and unstable (δ<0) regions.
Now we need to ask on which side of the neutral surface the unstable region
is located. We consider the straight line x = 1 and investigate the behavior of δ
along this line for increasing y.Forx = 1wefindk
4
x
= 2λ
4
. Next we substitute
this identity into the instability condition (24.34) and then multiply the resulting
expression by the positive quantity
M
2
=
2
2λ
2
+ k
2
x
2
β
2
> 0(24.44)
yielding
M
2
δ = 1 − y
2
(24.45)
For y<1 the discriminant δ>0; for y>1 the discriminant δ<0. Thus, the
stable and unstable regions are located as indicated in Figure 24.5. The boundary
point (x = 1,y = 1) corresponds to a point on the neutral curve.
24.4.3 Unconditional stability regions, the dominating wavelength
Inspection of Figure 24.5 shows that the solution is stable in the region y<1
for all x values, i.e. independently of the wavelength L
x
. This situation relates the
vertical shear of the horizontal wind field U
−
to the atmospheric stability σ
0
as
U
−
<
(p )
2
β
2f
2
0
σ
0
(24.46)
The region x>2 is stable for all values of y, i.e. stability is guaranteed to be
independent of U
−
, which is a measure of the baroclinicity of the atmosphere.
From (24.42) we obtain the corresponding stability condition
L
x
<
π
√
2 p
f
0
σ
0
(24.47)
