Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


23.9 The Philipps approximation of the ageostrophic component 611
Philipps made two basic assumptions.
(i) In order to partly restore the loss of the latitudinal variability of the Coriolis parameter,
he replaced the first term on the right-hand side of (23.60) by the original geostrophic
wind v
g
.
(ii) The individual derivative d/dt is approximated by d
g,0
/dt as given by
d
g,0
dt
=
∂
∂t
+ v
g,0
·∇
h
(23.64)
Introduction of these two assumptions into equation (23.60) gives the approxima-
tion
v
h
=
2 −
f
f
0
v
g,0
+
1
f
0
k ×
d
g,0
v
g,0
dt
(23.65)
which is known as the Philipps wind.
Now we are ready to derive the ageostrophic component of the horizontal wind
in the p system. For simplicity we omit the suffix p. First we evaluate the second
term on the right-hand side of (23.65) as
1
f
0
k ×
d
g,0
v
g,0
dt
=
1
f
0
k ×
∂v
g,0
∂t
+
1
f
0
k × (v
g,0
·∇
h
v
g,0
)
=−
1
f
2
0
∇
h
∂φ
∂t
+
1
2f
0
k ×∇
h
v
2
g,0
−
1
f
0
k × [v
g,0
× (∇
h
× v
g,0
)]
=−
1
f
2
0
∇
h
∂φ
∂t
+
1
2f
3
0
k ×∇
h
(∇
h
φ)
2
−
1
f
2
0
v
g,0
∇
2
h
φ
since v
2
g,0
=
1
f
2
0
(k ×∇
h
φ) · (k ×∇
h
φ) =
1
f
2
0
(∇
h
φ)
2
and k ×[v
g,0
× (∇
h
× v
g,0
)] =
1
f
0
v
g,0
∇
2
h
φ
(23.66)
In this expression use of (M1.48) and of the Lamb development (M3.75) has been
made. By utilizing (23.66) we obtain a suitable expression for the ageostrophic
wind component:
v
ag
= v
h
− v
g,0
=
1 −
f
f
0
v
g,0
−
1
f
2
0
∇
h
∂φ
∂t
+
1
2f
3
0
k ×∇
h
(∇
h
φ)
2
−
1
f
2
0
v
g,0
∇
2
h
φ
= v
ag
(I) + v
ag
(II) + v
ag
(III) + v
ag
(IV)
(23.67)
This geostrophic deviation is largely responsible for the occurrence of large-scale
changes in weather. The four terms of equation (23.67) will now be discussed
individually.

612 A quasi-geostrophic baroclinic model
A
B
g
g,0
g
h
h
h
C
Fig. 23.6 A schematic interpretation of the latitude effect, term v
ag
(I) of equation (23.67).
Fig. 23.7 A schematic interpretation of the pressur
e-tendency effect, term
v
ag
(II) of equa-
tion (23.67).
23.9.1 The latitude effect
Figure 23.6 shows idealized contour lines of φ and the corresponding geostrophic
wind v
g,0
at points A, B, and C. The Coriolis parameter f changes with latitude
in such a way that f<f
0
in the south, that is below the dashed line, while in
the north f>f
0
. From (23.67) we see that the first term on the right-hand side
yields
|
v
h
|
>
v
g,0
at point B while
|
v
h
|
<
v
g,0
at points A and C. Owing to its
latitudinal dependency, this term is called the latitude effect.
23.9.2 The pressure-tendency effect
The effect of the second term on the right-hand side of (23.67) is easily illustrated.
For simplicity we assume that circular isallobaric tendencies pertain. In a region
of falling pressure the gradient of ∂φ/∂t is directed away from the center of the
system so that the ageostrophic component resulting from the second term has the
opposite direction; see Figure 23.7(a). This implies that, due to mass transport,
the system is filling or decreasing in strength. In a region of rising pressure the
opposite effect will be observed; see Figure 23.7(b). With the help of (M4.51) it
is easy to show that height tendencies of pressure surfaces may be converted to
pressure tendencies ∂p/∂t at fixed levels by means of (∂p/∂t)
z
= ρ(∂φ/∂t)
p
. Thus
23.9 The Philipps approximation of the ageostrophic component 613
Fig. 23.8 A schematic interpretation of the confluence effect, term v
ag
(III) of equation
(23.67).
isolines of ∂φ/∂t may be relabelled as isallobars, which are isolines of ∂p/∂t or
vice versa.
The term −(1/f
2
0
) ∇
h
(∂φ/∂t) is known as the isallobaric or the Brunt–Douglas
wind after the two scientists who first formulated this expression in the year 1928.
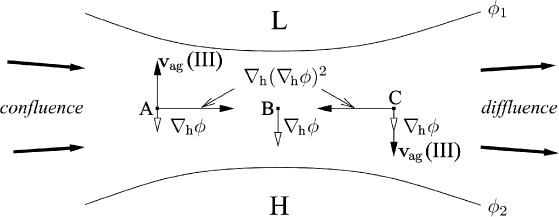
23.9.3 The confluence and diffluence effect
This kinematic effect is best demonstrated for regions of confluence and diffluence,
which must not be confused with regions of convergence and divergence. Conflu-
ence and diffluence refer to converging and diverging contour lines or isobars. Let
us consider an air parcel moving from the west to the east; see Figure 23.8. We
assume that initially the wind is in geostrophic balance. As the air approaches a
region with a stronger geopotential gradient, the geopotential gradient force −∇
h
φ
will exceed the Coriolis force so that the ageostrophic component is directed
toward the low pressure; see point A of Figure 23.8. Let us assume that, at the
point B, the geostrophic balance has been restored so that v
ag
(III) = 0. Because
the air is approaching a region with a weaker geopotential gradient, the Coriolis
force exceeds the geopotential gradient force, so the ageostrophic wind is directed
toward the higher pressure; see point C of Figure 23.8. In summary, in a region of
confluence the ageostrophic wind is directed toward the low pressure, whereas in
a region of diffluence the ageostrophic wind is directed toward the high pressure.
This effect is known as the confluence and diffluence effect.
23.9.4 The curvature effect
The fourth term on the right-hand side describes the so-called curvature effect
and is schematically illustrated in Figure 23.9. The Laplacian of φ is negative in

614 A quasi-geostrophic baroclinic model
Fig. 23.9 A schematic interpretation of the curvature effect, term v
ag
(IV) of equation
(23.67).
a high-pressure region but positive in a low-pressure region. Since in (23.67) the
term appears with a negative sign, we find that the horizontal wind |v
h
| > |v
g,0
| at
points A and C while |v
h
| < |v
g,0
| at point B.
23.10 Applications of the Philipps wind
We multiply equation (23.65) scalarly by the horizontal gradient of the geopotential
and obtain
v
h
·∇
h
φ =
2 −
f
f
0
1
f
0
k ×∇
h
φ
·∇
h
φ +
1
f
0
k ×
d
g,0
v
g,0
dt
·∇
h
φ
=−
k ×
d
g,0
v
g,0
dt
· (k × v
g,0
) =−
d
g,0
v
g,0
dt
· v
g,0
=−
d
g,0
dt
v
2
g,0
2
(23.68)
This is the selective geostrophic approximation of the kinetic energy of the horizon-
tal motion. It should be observed that the horizontal advection of the geopotential
involves the actual wind. Had we replaced the actual wind in the advection term
by the geostrophic wind, this term would have vanished. Thus, the change in
kinetic energy is given by the horizontal advection of the geopotential with the
ageostrophic wind component.
In Section 23.7 we have discussed the geostrophic approximation of the vorticity
equation, regarding which we had to use a number of arguments to justify the
procedure. With the help of the Philipps wind this approximation follows very
easily. Utilizing the Lamb development (M3.75), we expand (23.65) with the help

23.10 Applications of the Philipps wind 615
of (23.66) and obtain
v
h
= 2v
g,0
−
f
f
0
v
g,0
+
1
f
0
k ×
∂v
g,0
∂t
+
1
f
0
k ×
∇
h
v
2
g,0
2
+ (∇
h
× v
g,0
) × v
g,0
= 2v
g,0
−
f
f
0
v
g,0
+
1
f
0
k ×
∂v
g,0
∂t
+
1
f
0
k ×∇
h
v
2
g,0
2
−
1
f
0
ζ
g,0
v
g,0
(23.69)
with ζ
g,0
= k ·∇
h
× v
g,0
. Now we take the horizontal divergence of (23.69) and
recall that the divergence of v
g,0
is zero. The resulting equation
∇
h
· v
h
=−
1
f
0
v
g,0
·∇
h
f −
1
f
0
k ·∇
h
×
∂v
g,0
∂t
−
1
f
0
v
g,0
·∇
h
ζ
g,0
(23.70)
is already the desired result which is particularly suitable for physical interpretation.
The usual form (23.46) of the geostrophic approximation can be obtained by
rewriting (23.70) as
−f
0
∇
h
· v
h
=
d
g,0
η
g,0
dt
(23.71)
Utilizing (23.17) and (23.18) gives the final form
∇
2
h
∂φ
∂t
+ J
φ,
1
f
0
∇
2
h
φ + f
=−f
2
0
∇
h
· v
h
(23.72)
which is identical with (23.46). This partial differential equation describing the
tendency of the geopotential field apparently involves the three field quantities
(u, v, φ). On replacing the divergence term by means of the continuity equation we
recognize that this equation involves only the two variables ω and φ.Thevertical
velocity is found from the ω equation.
Now we will present a physical interpretation of the geostrophic approximation
of the vorticity equation (23.70).
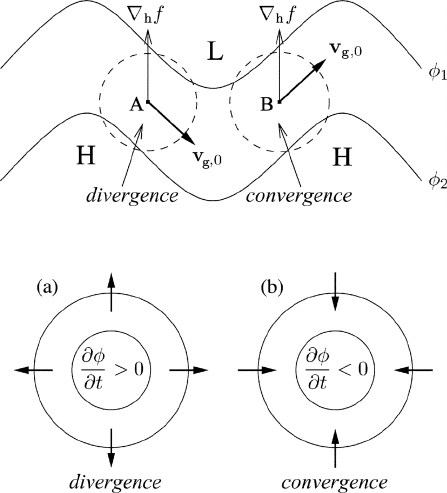
23.10.1 Westward displacement of a pressure system
Let us consider the idealized contour pattern of Figure 23.10. The gradient of
the Coriolis parameter, of course, is pointing to the north. In region A we have
cos(v
g,0
, ∇
h
f ) < 0 while in region B scalar product is positive. Owing to the
negative sign, the first term on the right-hand side of (23.70) produces divergence
in region A and convergence in region B. This results in a westward displacement
of the wave, which is known as the β effect since
|
∇
h
f
|
= β.
616 A quasi-geostrophic baroclinic model
Fig. 23.10 A schematic interpretation of the term −(1/f
0
)v
g,0
·∇
h
f of equation (23.70).
Fig. 23.11 A schematic interpretation of the term −(1/f
0
)k ·∇
h
× ∂v
g,0
/∂t =
−(1/f
2
0
)∇
2
h
∂φ/∂t of equation (23.70).
23.10.2 The pressure-tendency effect
Let us assume that we have an idealized circular pattern of the geopotential ten-
dency whose magnitude is largest at the center. The sign of the term determines
whether divergence or convergence occurs. For a positive tendency the Lapla-
cian of this quantity is negative. The resulting divergence opposes the effect of
the pressure tendency, as displayed in Figure 23.11(a). In case of a negative ten-
dency the Laplacian of the pressure tendency is positive, so the opposite situation
occurs.
23.10.3 The curvature effect
Again we consider sinusoidal contour lines, see Figure 23.12. In region A we
observe cos(v
g,0
, ∇
h
ζ
g,0
) > 0 resulting in convergence while in region B the scalar
product is negative, thus producing divergence. This term, often called the curvature
effect, results in an eastward displacement of the Rossby wave. Hence, the curvature
effect opposes the β effect. Usually the shorter Rossby waves move from west to
east, so the curvature effect dominates over the β effect. On the other hand, very
long Rossby waves move from east to west, so in this case the β effect dominates

23.11 Problems 617
Fig. 23.12 A schematic interpretation of the term −(1/f
0
)v
g,0
·∇
h
ζ
g,0
of equation (23.70).
over the curvature effect. There exists a critical wavelength, see Chapter 16, at
which standing Rossby waves form, resulting in blocking high- and low-pressure
systems.
23.11 Problems
23.1: Show that
σ
0
>0 stable atmosphere, ∂θ/∂z > 0
=0 neutral atmosphere, ∂θ/∂z = 0
<0 unstable atmosphere, ∂θ/∂z < 0
Start your derivation with the definition of σ
0
given in (23.9).
23.2:
(a) Consider the heat equation c
p
dT/dt−(1/ρ) dp/dt = B/ρ,whereB represents
the non-adiabatic terms. With the help of the hydrostatic approximation and the
continuity equation written in the (x,y,σ)system(σ = p/p
s
), show that the heat
equation can be written in the form
∂
∂t
∂φ
∂σ
+ v
h
·∇
h,σ
∂φ
∂σ
+ ˙σ
∂
2
φ
∂σ
2
+
∂φ
∂σ
1 − k
σ
+ k
∂φ
∂σ
∇
h,σ
· v
h
+ k
∂φ
∂σ
∂ ˙σ
∂σ
=
k
σp
s
∂φ
∂σ
B
with k = R
0
/c
p
.
(b) Show that
∂
2
φ
∂σ
2
+
∂φ
∂σ
1 − k
σ
=
1
g
∂φ
∂σ
2
∂ ln θ
∂z

618 A quasi-geostrophic baroclinic model
23.3: The Richardson equation is a diagnostic equation for the vertical velocity w
if the fields of the horizontal wind and the pressure are known. This equation can
be derived with the help of the continuity equation and the equation of an adiabat
which is given by p = constant × ρ
κ
,whereκ = c
p
/c
v
.
(a) Show that the Richardson equation in the z system can be written in the form
∂
∂z
p
∂w
∂z
=−
∂
∂z
(p ∇
h
·v
h
) +
1
κ
∂p
∂z
∇
h
· v
h
−
∂v
h
∂z
·∇
h
p
if the hydrostatic equation is assumed to be valid.
(b) Compare the Richardson equation with the ω equation. Hint: First show that
dρ
dt
=
1
g
∂p
∂z
∇
h
·v
h
+
∂w
∂z
23.4:
(a) Find the solution to the differential equation (23.55) by assuming that f = f
0
.
The initial conditions are q = q
0
and q
g
= q
g
(0).
(b) State the conditions under which the wind is geostrophic at all times. Give the
form of the corresponding geopotential field.

24
A two-level prognostic model, baroclinic instability
24.1 Introduction
In this chapter we are going to discuss the two-level quasi-geostrophic prediction
model. This model divides the atmosphere into four layers as shown in Figure 24.1.
The vorticity equation is applied to levels l = 1andl = 3 while the heat equation
is applied to level l = 2. By eliminating the vertical velocity ω it becomes possible
to determine the tendency of the geopotential ∂φ/∂t. Initially only the geopotential
φ(x,y, p, t
0
= 0) for the entire vertical pressure range 0 ≤ p ≤ p
0
must be
available. The discussion will be facilitated by resolving the dependent variables in
the vertical direction only. The remaining differentials will be left in their original
forms, which may be approximated by finite differences whenever desired.
In the second part of this chapter we are going to discuss the concept of
baroclinic instability. In a rotating atmosphere this type of instability, which was
first investigated by Charney (1947) and Eady (1949), arises from the vertical wind
shear if the static stability is not too large. The stability properties of the Charney
model are difficult to analyze. The two-level model, however, makes it possible
to obtain the stability criteria in a rather simple way, with results consistent with
Charney’s model. Details, for example, are given by Haltiner and Williams (1980).
24.2 The mathematical development of the two-level model
The basic system consists of the vorticity equation (23.44) and the first law of
thermodynamics (23.19). These equations are restated in slightly changed forms as
∂
∂t
+ v
g
·∇
h
(ζ
g
+ f ) = f
0
∂ω
∂p
+ K
h
∇
2
h
ζ
g
∂
∂t
+ v
g
·∇
h
∂ψ
∂p
=−
σ
0
ω
f
0
−
R
0
c
p,0
f
0
p
d
q
dt
(24.1)
619
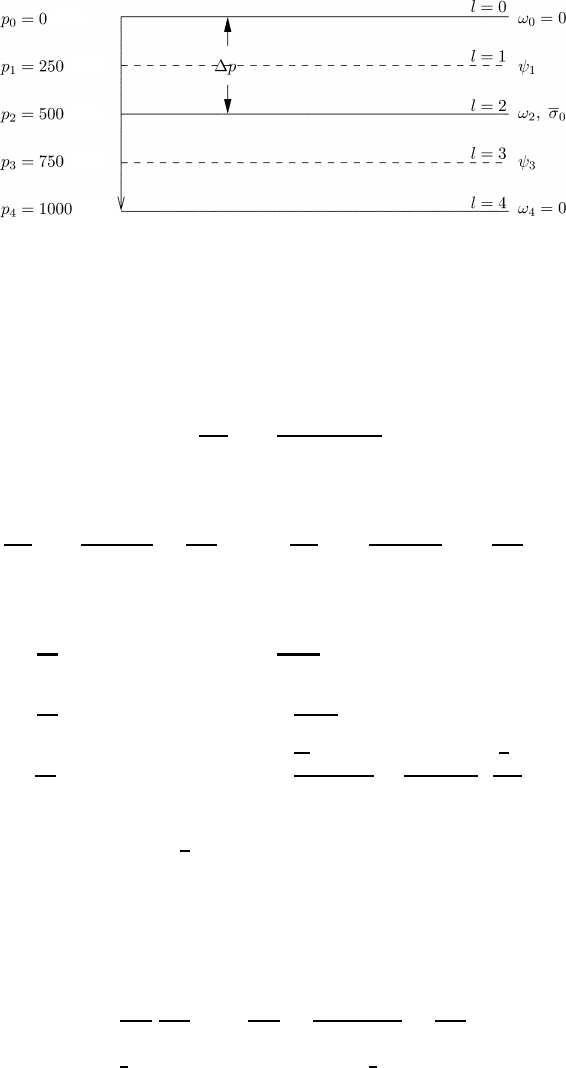
620 A two-level prognostic model, baroclinic instability
hPa
hPa
hPa
hPa
hPa
Fig. 24.1 The vertical grid structure of the two-level model.
In (24.1) we have also added the term K
h
∇
2
h
ζ
g
to simulate large-scale horizontal
diffusion, where K
h
is a large-scale diffusion constant. Furthermore, heat sources
have been included on the right-hand side of (24.1). The vertical derivative of the
arbitrary field function B will be approximated by
∂B
∂p
l
=
B
l+1
− B
l−1
p
(24.2)
see Figure 24.1, so the vertical derivative of ω at levels l = 1, 3isgivenby
∂ω
∂p
1
=
ω
2
− ω
0
p
=
ω
2
p
,
∂ω
∂p
3
=
ω
4
− ω
2
p
=−
ω
2
p
(24.3)
Thus, the basic system can also be written as
(a)
∂
∂t
+ v
g,1
·∇
h
(ζ
g,1
+ f ) =
f
0
ω
2
p
+ K
h
∇
2
h
ζ
g,1
(b)
∂
∂t
+ v
g,3
·∇
h
(ζ
g,3
+ f ) =−
f
0
ω
2
p
+ K
h
∇
2
h
ζ
g,3
(c)
∂
∂t
+ v
g,2
·∇
h
(ψ
3
− ψ
1
) =−
σ
0
ω
2
p
f
0
−
R
0
p
c
p,0
f
0
p
2
d
q
dt
2
(24.4)
For the simple theory which is presented here this type of parameterization will be
sufficient. The heating term d
q/dt simulates all essential heat sources, including
radiative effects.
In order to simplify the mathematical analysis of the problem we assume that we
have a linear distribution of the geostrophic wind within the range p
1
<p<p
3
.
Hence, we obtain
v
g,2
= v
g,1
+
∂v
g
∂p
p
2
,
∂v
g
∂p
=
v
g,3
− v
g,1
p
=
1
p
k ×∇
h
(ψ
3
− ψ
1
)
=⇒ v
g,2
= v
g,1
+
1
2
k ×∇
h
(ψ
3
− ψ
1
) = v
g,3
−
1
2
k ×∇
h
(ψ
3
− ψ
1
)
(24.5)
