Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

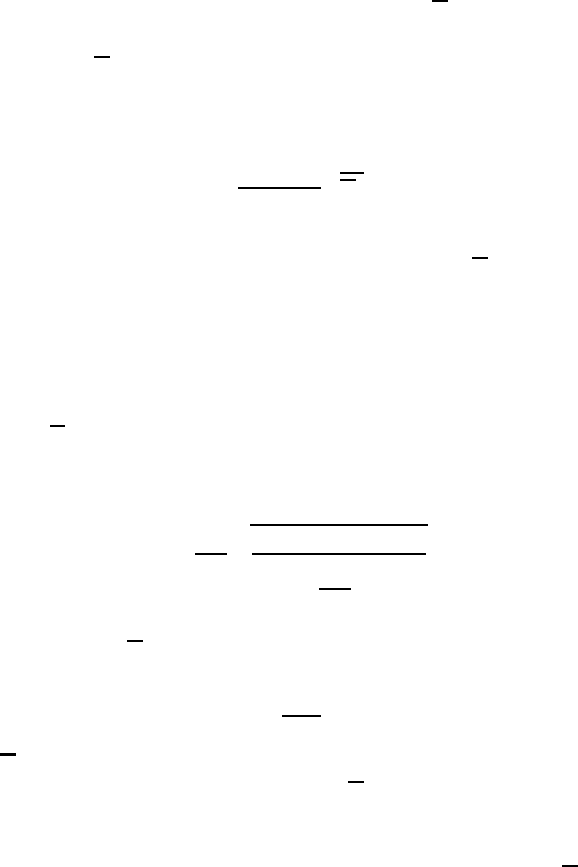
24.4 Baroclinic instability 631

showing that all waves with wavelengths shorter than the given value are stable,

independently of the baroclinicity U

−

From (24.42) we see that, for ﬁxed values of β and σ

, instability will be

generated if the baroclinicity U

−

increases to large enough values. Instability will

also be generated if

becomes small enough for ﬁxed values of β and U

−

.The

wavelength corresponding to x = 1 is of particular interest since, for increasing

y, the unstable region is reached faster than at any other point on the x-axis. This

condition yields

3/4

πp



(24.48)

as follows from (24.42). The wavelength deﬁned by this equation is known as the

dominating wavelength and is proportional to the static stability

. It follows that,

with increasing static stability, waves of increasing wavelength will dominate.

24.4.4 Neutral surfaces in the (U

−

)-plane

The representation of the neutral curve in the (U

−

)-plane is particularly easy to

visualize. Now σ

and β serve as parameters with which to label curves belonging

to the same family. Suppose that we set β = constant. Using the deﬁnition (24.42),

the equation of the neutral curve can now be written as

−

=±

2λ







1 −



2λ



− 1



(24.49)

In the limiting case that

= 0orλ →∞, we ﬁnd after a few easy steps that U

−

is the parabola

−

βL

8π

(24.50)

Thus, for σ

= 0 we ﬁnd the parabola depicted in Figure 24.6. The area above the

curve represents the unstable region. For values

> 0 we obtain from (24.49)

the family of curves shown in Figure 24.6. Hence, with increasing static stability

the area of the unstable region decreases in size.

Reference to equation (23.20b) shows that, in the ﬁltered model, for

= 0

changes in temperature are caused by horizontal advection only. Models in which

the static stability is set equal to zero are called advection models.Inthese

models the short waves are always unstable, as follows from Figure 24.6.

Using the terminology of optics, very short waves of the solar spectrum are located

in the ultra-violet spectral region. Therefore, the unconditional instability for short

waves in the advection models is called the ultra-violet catastrophy.

632 A two-level prognostic model, baroclinic instability

Fig. 24.6 A schematic representation of the neutral curves for β = constant and varying

static stability σ

with (σ

)

> (σ

)

Fig. 24.7 A schematic representation of the effect of β on the region of instability for the

limiting case

= 0 with β

>β

Suppose that we vary the Rossby parameter β. From (24.50) we then obtain a

family of parabolas as shown in Figure 24.7. The unstable region for each β is

on the left-hand side of the corresponding parabola. This is best recognized by

considering the stability condition (24.34) whereby increasing values of β prevent

δ from becoming negative.

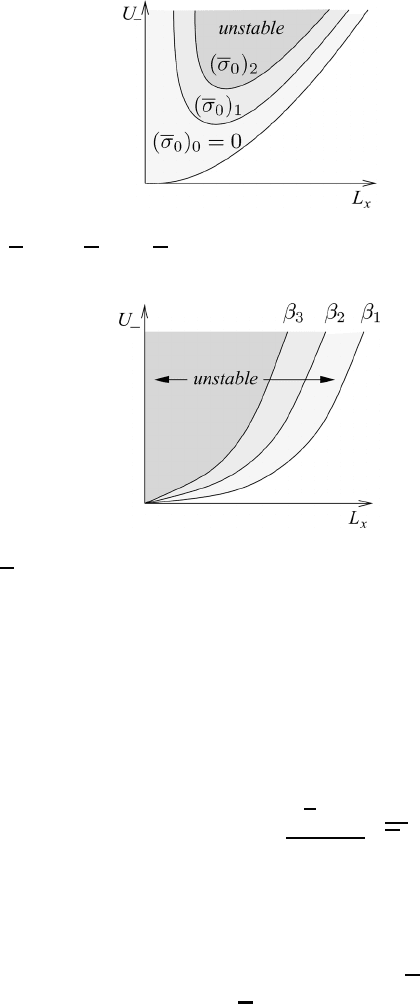
Let us now consider the special case that β = 0. From (24.34) we ﬁnd for δ = 0

2λ

= k

=⇒ L

√

2πp



(24.51)

which represents a family of vertical lines. It stands to reason that, with increasing

static stability, the stable region must increase in size, as shown in Figure 24.8.

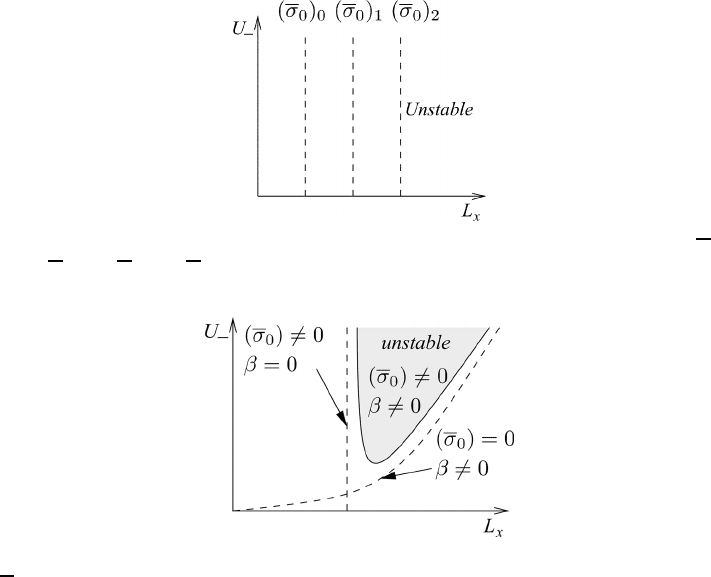
From the previous ﬁgures we may conclude that short and long waves are stable

in the quasi-geostrophic theory provided that β = 0and

= 0. Moreover, we

observe that increasing values of β and σ

have a stabilizing effect. By combining

the results of this section we ﬁnd Figure 24.9.

We wish to point out that the results derived from the two-level model are

not sufﬁciently representative to permit us to draw general conclusions about the

24.5 Problems 633

Fig. 24.8 A schematic display of neutral curves for β = 0 and variable static stability σ

with (σ

)

> (σ

)

> (σ

)

Fig. 24.9 The reg

ion of instability in the (

−

)-plane for

the general case

β = 0and

= 0.

baroclinic instability of the real atmosphere. Nevertheless, the two-level model

provides at least qualitatively the major characteristics of baroclinic instability and

yields results consistent with the more general model proposed by Charney (1947).

24.5 Problems

24.1: Show in detail the steps between equation (24.25) and (24.28).

24.2: Use calculus to verify the minimum of Figure 24.5.

An excursion concerning numerical procedures

In order to solve the atmospheric equations it is necessary to apply numeri-

cal methods. It is not our intention to present a detailed discussion on numerical

methods since this would require a separate textbook of many chapters. An early

book on numerical methods applicable to atmospheric dynamics was written by

Thompson (1961). It is quite suitable as a ﬁrst introduction to numerical weather

analysis. A more modern and extensive account of numerical methods is that by

Haltiner and Williams (1980). Both books may be consulted regarding the follow-

ing discussion. There also exist many papers and reports on the subject, which are

too numerous to be quoted here. In this chapter we wish to point out some problems

that may arise when one is using ﬁnite-difference methods. In fact, many numer-

ical problems become apparent even in treating the one-dimensional advection

equation.

25.1 Numerical stability of the one-dimensional advection equation

25.1.1 Introduction

The typical appearance of numerical instability in analytic form can be easily

recognized from the discretized form of the one-dimensional advection equation:

∂ψ

∂t

+ U

∂ψ

∂x

= 0withU = constant (25.1)

This is a linear ﬁrst-order partial differential equation whose solution is given by

f (x − Ut), where f is an arbitrary function. A special solution is the harmonic

wave

ψ = A exp[ik(x − Ut)] (25.2)

where k = 2π/L is the wavenumber and L the wavelength. Equation (25.1)

shall now be discretized in various ways in order to compare the solutions of the

634

25.1 Numerical stability 635

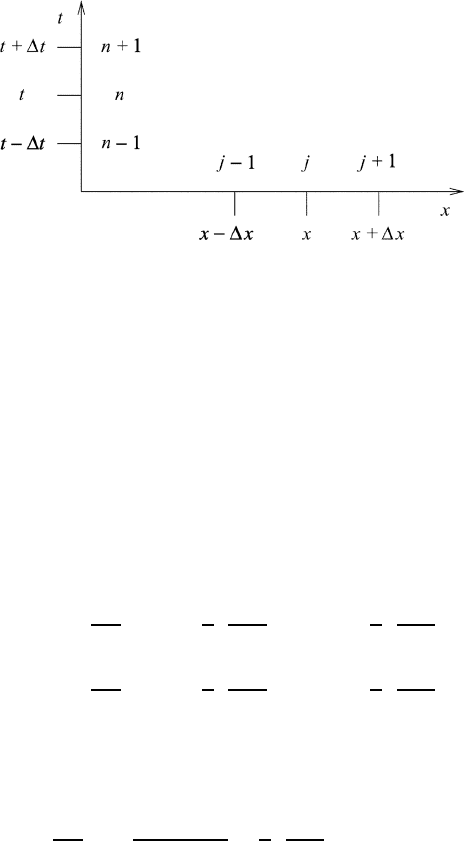
Fig. 25.1 The grid structure in space and time for one spatial dimension. The spatial

distance x is counted in units of jxwhile time t is advanced in units of nt.

difference equations with the solution (25.2). This procedure will permit us to study

the stability behavior in terms of time for various numerical schemes.

The ﬁnite-difference equations can be constructed in various ways. We will

obtain these by expanding the function f (x − Ut) in a Taylor series of only one

spatial dimension as shown in Figure 25.1. Let us ﬁrst obtain ﬁnite-difference

expressions with which to approximate the partial derivative ∂ψ/∂x.

The Taylor-series expansions about the point j in forward and backward direc-

tions are given by

(a) ψ

j+1

= ψ



∂ψ

∂x



x +



∂

∂x



(x)



∂

∂x



(x)

+···

(b) ψ

j−1

= ψ

−



∂ψ

∂x



x +



∂

∂x



(x)

−



∂

∂x



(x)

+···

(25.3)

From (25.3a) we ﬁnd, for ﬁxed time t, indicated by the superscript n,theﬁnite-

difference equation in the forward direction:



∂ψ

∂x



j+1

− ψ

x

−



∂

∂x



x +··· (25.4a)

The terms following the ﬁnite-difference terms are dominated by a second-order

derivative, which is multiplied by x. By ignoring this term and all other terms in-

volving higher derivatives we have introduced a ﬁrst-order truncation error O(x)

since x appears as a ﬁrst power. From (25.3b) we could have obtained a similar

approximation in the backward direction, which involves the point j − 1 instead

of j + 1. Since we do not use the backward approximation, we will not write it

down. The ﬁrst term on the right-hand side of (25.4a) is known as the forward-in-

space difference approximation to ∂ψ/∂x. On subtracting (25.3b) from (25.3a) the

636 An excursion concerning numerical procedures

second-order derivatives will vanish. The remaining terms are dominated by a term

involving the third-order derivative at point j multiplied by x

.Ondividingby

x we obtain the so-called central ﬁnite-difference approximation to the ﬁrst-order

derivative:



∂ψ

∂x



j+1

− ψ

j−1

2 x

−



∂

∂x



(x)

+··· (25.4b)

which is the ﬁrst term on the right-hand side of (25.4b). By ignoring all terms

involving higher-order derivatives we obtain a better approximation to the derivative

∂ψ/∂x since now the truncation error is of second order, O



(x)



In order to obtain approximations to the time derivative we proceed in a similar

manner. Then we obtain expressions analogous to (25.3), where now j is ﬁxed and

n is varied. We will now apply the various difference approximations.

25.1.2 The numerical phase speed

The advection equation (25.1) in discretized form using central differences in time

and space now reads

n+1

− ψ

n−1

+ U

t

x



j+1

− ψ

j−1



= 0(25.5)

The solution to this ﬁnite-difference equation is found by substituting a trial grid-

point function of the type (25.2) of the analytic solution into (25.5):

(a) ψ

= A exp[ik(jx− cn t)]

(b) ψ

n+1

= A exp{ik[jx− c(n + 1)] t}=ψ

exp(−ikc t)

n−1

= ψ

exp(ikc t)

(d) ψ

j+1

= ψ

exp(ik x)

(e) ψ

j−1

= ψ

exp(−ik x)

(25.6)

Here U has been replaced by the phase speed c = ω/k,whereω is the circular

frequency. The trial solution is identical with (25.2) only if c = U. Substitution of

(25.6) into (25.5), after canceling out the common factor ψ

,gives

exp(ikc t) − exp(−ikc t) =

Ut

x

[exp(ik x) − exp(−ik x)] (25.7)

Dividing both sides of this equation by 2i (i =

√

−1) and using the Euler expansion

gives the frequency equation

sin(kc t) =

Ut

x

sin(kx)(25.8)

25.1 Numerical stability 637

The numerical phase speed follows immediately and is given by

c =

kt

arcsin



Ut

x

sin(kx)



(25.9)

Using

lim

x→0

sin(kx)

x

= k, lim

→0

arcsin 



= 1(25.10)

we ﬁnd for (x, t) −→ 0 the consistent result

lim

x,t→0

c = U (25.11)

25.1.3 Numerical instability

We now reconsider equation (25.9) and assume that

t

x

> 1(25.12)

Atthesametimewerequirethatsin(kx) in the argument of (25.9) reaches

the maximum possible value 1. Because kx = π/2 this corresponds to the

wavelength L = 4 x. In this case the argument of arcsin( ) is greater than 1 and

(25.9) can be satisﬁed only by complex values of the numerical phase speed,

c = c

± ic

(25.13)

In order to evaluate the real part c

and the imaginary part c

≥ 0 of the phase

speed, assuming the validity of (25.12), we go back to the frequency equation (25.8).

This equation now reads

sin(kc t) = sin(α

± iα

) = 1 +a, a > 0(25.14)

The complex number α

±iα

arises because of (25.13). The quantity a on the right-

hand side must be positive. Application of the trigonometric addition theorems

gives

(a) sin α

cos(iα

) ± sin(iα

)cosα

= 1 + a

(b) sin α

cosh α

± i sinh α

cos α

= 1 + a

(25.15)

where we have introduced the hyperbolic functions in (25.15b). Comparison of

real and imaginary parts results in

(a) Real part: sin α

cosh α

= 1 +a

(b) Imaginary part: cos α

sinh α

= 0

(25.16)

638 An excursion concerning numerical procedures

Since we require that α

= kc

t = 0 it follows from (25.16b) that cos α

= 0, so

= kc

t =±

, ±

π,... (25.17)

For further discussion we select the representative value

2kt

(25.18)

On the other hand, with α

= π/2, from (25.16a) it follows that

cosh α

= cosh(kc

t) = 1 + a =⇒ c

cosh

−1

(1 + a)

kt

> 0(25.19)

From (25.6a), (25.18), and (25.19), assuming the validity of (25.12), we obtain the

general solution to (25.5):

= A

exp[ik(jx− c

nt −ic

nt)]

+ A

exp[ik(jx− c

nt + ic

nt)]

(25.20)

Owing to (25.18) this expression may be rewritten in such a way that

= A

exp(ikj x)(−i)

exp(kc

nt) + A

exp(ikj x)(−i)

exp(−kc

nt)

(25.21)

since in this case exp(−ikc

nt) = exp(−inπ/2) = (−i)

. Because c

> 0the

ﬁrst term with alternating sign approaches inﬁnity for large n, thus indicating

numerical instability. The second term with alternating sign in (25.21) approaches

zero. We conclude that the numerical solution in the present case using central

difference quotients in time and space is stable only if the condition (25.12) is

changed to

t

x

≤ 1ort ≤

x

(25.22)

In this case the phase velocity is real and the solution remains stable. Equation

(25.22) is the well-known Courant–Friedrichs–Lewy (CFL) stability criterion for

the case of the linear difference equation which we have considered here.

Equation (25.22) can be usefully interpreted. Numerical stability occurs when-

ever the time step t is smaller than the time required for the wave moving with

phase speed U to cover the grid distance x.

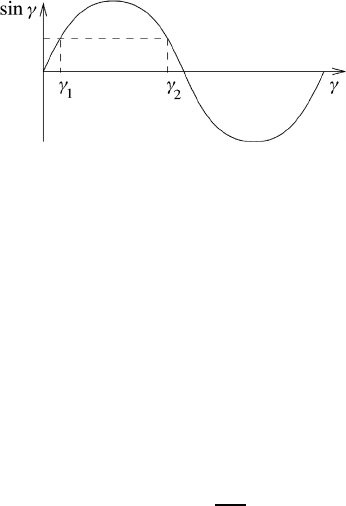
25.1 Numerical stability 639

Fig. 25.2 Ambiguity of phase velocities.

25.1.4 The so-called weak instability

Even if the CFL criterion (25.22) is obeyed we still do not obtain an absolutely

stable numerical behavior. The phase velocity c according to (25.9) now assumes

real values, as desired. The arcsine function, however, admits two different real

phase velocities c

1,2

, in contrast to the analytic solution (25.2) of (25.1), which

admits the phase velocity c = U only. Owing to sin γ

= sin γ

with γ

= π − γ

see Figure 25.2, the frequency equation (25.8) is satisﬁed by

= c

kt = arcsin



t

x

sin(kx)



= c

kt = π − c

kt

(25.23)

With decreasing x, t −→ 0 these two phase velocities become

lim

t,x→0

= U, lim

t,x→0

=∞ (25.24)

One part of the solution with c

= U is physically real; the other part with

=∞is a wave due to the numerical procedure and, therefore, is counted

as a weak instability. The artiﬁcial numerical wave is caused by the difference

equation (25.5), which requires for the forecast knowledge of ψ at two initial

times ψ

j−1

,ψ

j+1

,ψ

n−1

whereas for the analytic solution of (25.1) only one initial

condition is needed. The requirement of a second initial condition is responsible

for the existence of the numerical wave with phase velocity c

In order to discuss the behavior of the numerical wave we substitute c

and

according to (25.23) into the complete numerical solution. According to the

principle of superposition we ﬁnd

= A

exp[ik(jx− c

nt)] + A

(−1)

exp[ik(jx+ c

nt)] (25.25)

since exp(−inπ) = (−1)

. The second term on the right-hand side is the numerical

640 An excursion concerning numerical procedures

wave whose amplitude changes sign with each time step. Moreover, by recalling

that the analytic solution is given by f (x −Ut), it is easily seen that the numerical

wave moves in a direction opposite to the physical wave.

The amplitudes A

and A

will be determined from the initial conditions with

the goal of eliminating the numerical wave. From (25.25) we ﬁnd

n=0

= A

exp(ikj x) + A

exp(ikj x)

n=1

= A

exp[ik(jx− c

t)] − A

exp[ik(jx+ c

t)]

(25.26)

The ﬁrst predicted value of ψ then refers to n = 2. In order to eliminate A

multiply the ﬁrst equation by exp(−ikc

t) and then subtract the second equation.

From this it follows that

n=0

exp(−ikc

t) −ψ

n=1

exp(ikj x)[exp(ikc

t) +exp(−ikc

t)]

(25.27)

For A

to vanish we must set

n=1

= ψ

n=0

exp(−ikc

t)(25.28)

In this particular simple case we were able to relate the initial conditions. In practical

numerical weather prediction the differential equations to be solved numerically

are much more complicated, so the phase speed c is unknown. In a later section we

will show how to eliminate the numerical wave in a different manner.

25.2 Application of forward-in-time and central-in-space

difference quotients

In contrast to the previous sections we will now replace the local time derivative by

means of a forward-in-time difference quotient. Instead of (25.5) we now obtain

n+1

− ψ

Ut

2 x



j+1

− ψ

j−1



= 0(25.29)

In comparison with (25.5) the second initial value at time step n −1 is not needed,

resulting in only one phase velocity c. Now only one initial condition for t = 0or

n = 0 is required. Thus weak instability does not occur. We will now investigate

whether the remaining wave is numerically stable. We substitute the trial solution

(25.6a) into (25.29) and obtain after canceling out of ψ

the expression

exp(−ikc t) − 1 +

Ut

2 x

[exp(ik x) − exp(−ik x)] = 0(25.30)