Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

26.3 Horizontal discretization 661

(λ, θ) =



2n + 1

4π

(n − m)!

(n + m)!

(cos θ) exp(imλ) =

√

2π



(cos θ)exp(imλ)

(26.55)

Observing the orthogonality relation



2π

exp(imλ)exp(−im



λ) dλ = 2πδ

m,m



(26.56)

and the normalized form (26.51) of the associated Legendre polynomials, we may

easily verify the orthogonality relation



2π

dλ



−1

(λ, µ)





(λ, µ)



∗

dµ = δ

m,m



n,n



(26.57)

The superscript

∗

denotes the complex conjugate of the function Y

Equation (26.49) may be written in the more convenient form

(λ, θ) =



m=−n

(λ, θ)(26.58)

Equations (26.49) and (26.58) are completely equivalent, each requiring 2n + 1

expansion coefﬁcients.

26.3.2 Spectral representation

According to Sommerfeld (1964), equation (26.58) represents the most general

surface spherical harmonics. If we wish to represent a function f on the sphere we

must sum over all n so that

f (λ, µ) =

∞



n=0

∞



n=0



m=−n

(λ, µ)(26.59)

This expression, also known as Laplace’s series, is a uniformly convergent double

series of spherical harmonics. Now we wish to apply (26.59) to the prognostic

variables X = ζ,D,T,q,andlnp

, where the variables ζ and D are used instead

of U and V . Obviously, the meteorological variables vary on the surface of the

earth not only with the longitude λ and the latitude ϕ but also with the generalized

height ξ and with time. In order to use the series representation in the numerical

integrations it is necessary to truncate the series and retain only a ﬁnite number

of terms. We restrict the series expansion to m ≤ M and n −

≤ J ,whereM and

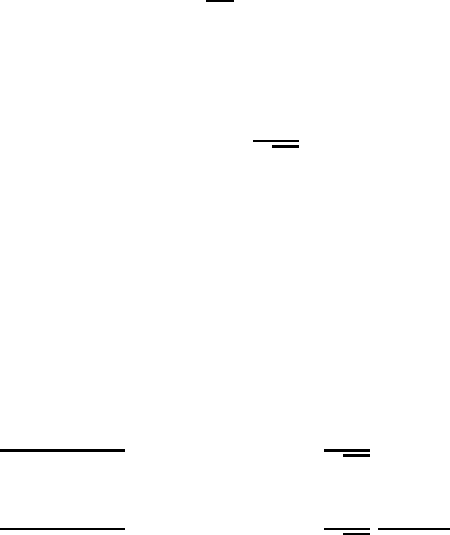
662 Modeling of atmospheric ﬂow by spectral techniques

J are positive integers. Thus, we write

X(λ, µ, ξ, t) =



m=−M



(ξ,t)Y

(λ, µ)(26.60)

In order to obtain expressions for the expansion coefﬁcients X

we make use of

the orthogonality relations (26.57). We obtain immediately the complex-valued

expression

(ξ,t) =



−1



2π

X(λ, µ, ξ, t)



(λ, µ)



∗

dλdµ (26.61)

Since X is real we recognize with the help of (26.53) that

−m

= (−1)





∗

(26.62)

In the complex representation of Fourier series, the Fourier coefﬁcients of X are

deﬁned by

(µ, ξ, t) =

2π



2π

X(λ, µ, ξ, t)exp(−imλ) dλ (26.63)

Substitution of (26.60) into (26.63) and using the orthogonality condition (26.56)

yields

(µ, ξ, t) =

√

2π



(ξ,t)



(µ)(26.64)

Therefore, (26.60) can be written as

X(λ, µ, ξ, t) =



m=−M

(µ, ξ, t) exp(imλ)(26.65)

Equations (26.60) and (26.43) can now be used to obtain the horizontal derivatives

of X entirely analytically:

∂X(λ, µ,ξ, t)

∂λ



m=−M



(ξ,t)

√

2π



(µ)exp(imλ)

∂X(λ, µ,ξ, t)

∂µ



m=−M



(ξ,t)

√

2π



(µ)

dµ

exp(imλ)

(26.66)

26.3 Horizontal discretization 663

The derivative of the associated Legendre polynomials involved in (26.66) can be

expressed by the following recurrence relation:

(1 − µ

)

dµ



(µ) =−n9

n+1



n+1

(µ) + (n + 1)9



n−1

(µ)

with 9



− m

− 1

(26.67)

We now multiply equation (26.35) by the factor 1/a

,wherea is the mean radius

of the earth. The ﬁrst two terms are equivalent to the horizontal Laplacian operator

in spherical coordinates. Thus we obtain

∇

(λ, µ) =−

n(n + 1)

(λ, µ)(26.68)

This important relation will be used shortly.

Next we need to formulate the spectral coefﬁcients for the vorticity and the

divergence. The mathematical process is not difﬁcult but is somewhat lengthy.

Therefore, the derivation will be done in several steps. The ﬁrst step is the formu-

lation of the Fourier coefﬁcients for U and V as stated by (26.23). Application of

equation (26.63) to U gives immediately

(µ, ξ, t) =

2πa



2π



−(1 − µ

)

∂ψ

∂µ

∂χ

∂λ



exp(−imλ) dλ (26.69)

Note that the stream function ψ and the velocity potential χ appear in differentiated

form. On replacing X in (26.66) by ψ andthenbyχ we ﬁnd

(µ, ξ, t) =

a(2π)

3/2





=−M









−(1 − µ

)ψ



(ξ,t)

dµ



(µ)

+ im



(ξ,t)



(µ)





2π

exp[i(m



− m)λ] dλ

(26.70)

For compactness of notation we will introduce

(µ) =−(1 − µ

)

dµ



(µ)(26.71)

into (26.70). Thus we ﬁnd

(µ, ξ, t) =

√

2π





(ξ,t)H

(µ) + imχ

(ξ,t)



(µ)



(26.72)

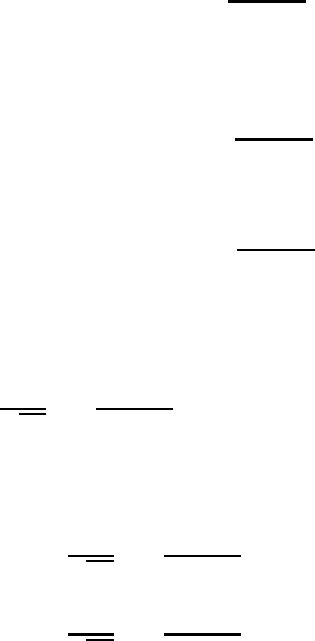
664 Modeling of atmospheric ﬂow by spectral techniques

Our next goal is to involve the vorticity and the divergence (see (26.24)) instead of

the stream function and the velocity potential. On expanding the vorticity according

to (26.60) we ﬁnd without difﬁculty

ζ (λ, µ, ξ, t) =



m=−M



(ξ,t)Y

(λ, µ)



m=−M



(ξ,t) ∇



(λ, µ)





m=−M



(ξ,t)



−

n(n + 1)



(λ, µ)

(26.73)

where we have used (26.68) to eliminate the Laplacian operator. Inspection of

(26.73) shows that

(ξ,t) =−ψ

(ξ,t)

n(n + 1)

(26.74)

Since ζ and D have the same mathematical structure, we obtain immediately

(ξ,t) =−χ

(ξ,t)

n(n + 1)

(26.75)

Substituting (26.74) and (26.75) into (26.73) expresses the Fourier coefﬁent U

terms of the spectral coefﬁcients ζ

and D

(µ, ξ, t) =−

√

2π



n(n + 1)



(ξ,t)H

(µ) + imD

(ξ,t)



(µ)



(26.76)

After introducing the deﬁnitions

(µ, ξ, t) =−

√

2π



n(n + 1)

(ξ,t)H

(µ)

(µ, ξ, t) =−

√

2π



iam

n(n + 1)

(ξ,t)



(µ)

(26.77)

we may write

(µ, ξ, t) = U

(µ, ξ, t) + U

(µ, ξ, t)(26.78)

Inspection of equations (26.23a) and (26.23b) reveals a certain symmetry in

the structure of the equations involving the stream function ψ and the velocity

26.3 Horizontal discretization 665

potential χ. This allows us to write down the spectral coefﬁcients for the velocity

components V

and V

without any additional work:

(µ, ξ, t) =−

√

2π



iam

n(n + 1)

(ξ,t)



(µ)

(µ, ξ, t) =

√

2π



n(n + 1)

(ξ,t)H

(µ)

(26.79)

In analogy to (26.78) we ﬁnd

(µ, ξ, t) = V

(µ, ξ, t) + V

(µ, ξ, t)(26.80)

The function H

(µ) is deﬁned by (26.71) and can be evaluated by means of the

recurrence relation (26.67).

Much work has gone into the formulation of a suitable truncation of the series

expression and various truncation schemes have been proposed. One rather simple

scheme is the so-called triangular scheme in which J = M. At present, this scheme

is being used operationally with J exceeding 100.

26.3.3 The spectral tendencies

The general form of the spectral model is based on the work of Bourke (1974) and

Hoskins and Simmons (1975). The formulation of the spectral tendencies for the

prognostic variables X = ζ,D,T,q,andlnp

given by (26.18), (26.21), (26.8b),

(26.9b), and (26.15) is accomplished with the help of equation (26.61). We will

demonstrate the procedure for the vorticity equation. The remaining prognostic

equations are handled likewise. We multiply both sides of equation (26.18) by

(λ, µ)]

∗

and then integrate over the sphere. For the left-hand side of the equation

we ﬁnd



−1



2π

∂

∂t

ζ (λ, µ, ξ, t)



(λ, µ)



∗

dλdµ =

∂

∂t

(ξ,t)(26.81)

so that the spectral tendency equation for the vorticity is given by

∂

∂t

(ξ,t) =



−1



2π



1 − µ

∂

∂λ

+ P

)

−

∂

∂µ

+ P

)





(λ, µ)



∗

dλdµ + (K

)

with (K

)



−1



2π



(λ, µ)



∗

dλdµ

(26.82)

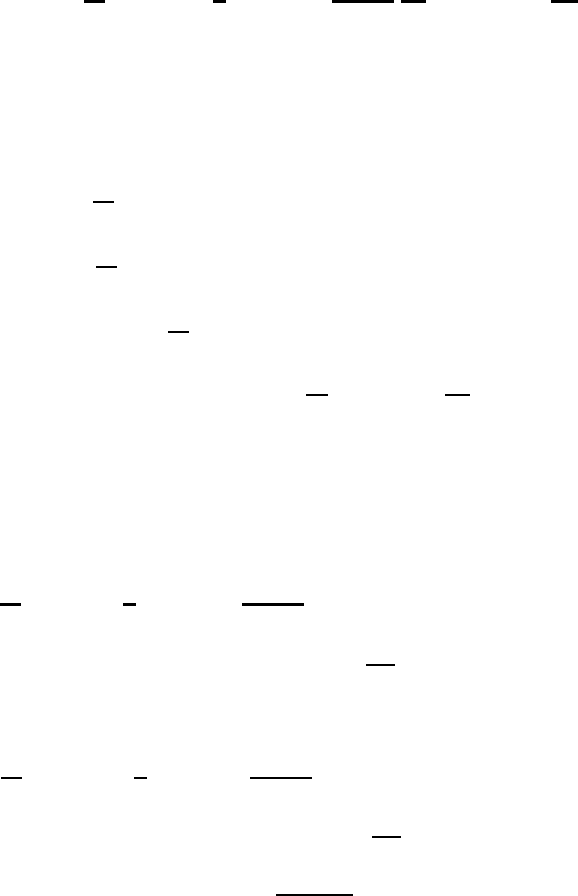
666 Modeling of atmospheric ﬂow by spectral techniques

Likewise, we ﬁnd

∂

∂t

(ξ,t) =



−1



2π



1 − µ

∂

∂λ

+ P

) +

∂

∂µ

+ P

)

− a ∇





(λ, µ)



∗

dλdµ + (K

)

with (K

)



−1



2π



(λ, µ)



∗

dλdµ

(26.83)

∂

∂t

(ξ,t) =



−1



2π

+ Q

)



(λ, µ)



∗

dλdµ (26.84)

∂

∂t

(ξ,t) =



−1



2π

+ Q

)



(λ, µ)



∗

dλdµ (26.85)

∂

∂t

(ln p

)



−1



2π



(λ, µ)



∗

dλdµ

with F

=−



∇



∂p

∂ξ



dξ

(26.86)

Equations (26.82) and (26.83) contain partial derivatives, which can be elimi-

nated by partial integration to bring them into the form of the remaining prognostic

equations. Observing that P

(±1) = 0(m>0) and using the cyclic boundary con-

dition (0, 2π ) which applies when one is integrating along a ﬁxed latitude circle,

we easily obtain

∂

∂t

(ξ,t) =



−1



2π



1 − µ

+ P

)



(λ, µ)



∗

+ (F

+ P

)

dµ



(λ, µ)



∗



dλdµ + (K

)

(26.87)

and

∂

∂t

(ξ,t) =



−1



2π



1 − µ

+ P

)



(λ, µ)



∗

− (F

+ P

)

dµ



(λ, µ)



∗

n(n + 1)



(λ, µ)



∗



dλdµ + (K

)

(26.88)

Every forecast requires a set of consistent initial data. In the ideal case these data

should be free from any imbalances between the wind and the mass ﬁeld. Sophisti-

cated procedures for providing such initial data sets have been worked out by var-

ious research groups. However, these initialization techniques are model-speciﬁc.

26.4 Problems 667

Here we will simply assume that such data sets exist for the prognostic variables

X = ζ,D,T,q,andlnp

on a suitable grid of points over the sphere. With the help

of equation (26.61) the quantities X



t=0

= ζ

,andlnp

can be com-

puted. These quantities are required for the ﬁrst time step in order to evaluate the

tendency equations (26.84)–(26.88). Moreover, the X



t=0

are sufﬁcient for calcu-

lating U

,andV

,soU

and V

can be found from (26.78) and (26.80).

With the help of (26.65) the velocity components U and V which are needed for

the evaluation of F

, F

in (26.18) and F

, F

in (26.8) and (26.9) can then be

found. The horizontal derivatives ∂T /∂λ, ∂T /∂µ, ∂q/∂λ, ∂q/∂µ, ∂ ln p

/∂λ,and

∂ ln p

/∂µ can be found analytically by summing (26.66) over m. This information

should also be sufﬁcient for computing F

in (26.86) and G in (26.21) as well

as all parameterized quantities. Since all ﬁeld quantities are evaluated at the same

grid points, the forecast can be started. Whenever desired, the conversion to the

variables X = ζ,D,T,q,andlnp

can be achieved with the help of (26.60).

To carry out the forecast, the model must contain a suitable vertical ﬁnite-

difference scheme to evaluate the terms involving the generalized vertical coor-

dinate ξ. There exist various suitable vertical schemes. In the earlier phases of

modeling the σ system (ξ = σ = p/p

) which satisﬁes the condition that σ = 0

at the top of the atmosphere and σ = 1 at the surface was used. We will omit any

discussion of the speciﬁc numerical procedures such as the evaluation of (K

)

and

)

since these are subject to continual revision. As stated before, the spectral

model is well suited for the application of the semi-implicit method. Following

Robert et al. (1972), the model uses such a scheme for the equations of divergence,

temperature, and the surface pressure. In addition, the model uses a semi-implicit

method for the zonal advection terms in various equations.

Many details, too numerous to be described here, are required for proper handling

of the model. For further information the original literature should be consulted.

26.4 Problems

26.1: Omitting the underlined terms in equation (19.15) and replacing the radius

r by the constant radius a, show that the horizontal components of the equation of

motion can be written as stated in (26.5a) and (26.5b). Ignore frictional effects.

26.2: Use equation (1.77) and the formulas stated in problem (1.8) to show that

the vorticity can be written in the form (26.6). Set r = a whenever r appears in

undifferentiated form.

26.3: Prove the validity of equation (26.19).

26.4: Show that the deﬁnition of ∇

stated in (26.21) is correct.

668 Modeling of atmospheric ﬂow by spectral techniques

26.5: Find P

(µ) and show that this function satisﬁes equation (26.37).

26.6: Differentiate Legendre’s equation (26.37) m times to prove the validity of

(26.39).

26.7: Show that equation (26.39) can be transformed to give equation (26.41) by

using the transformation (26.40).

26.8: Use the recurrence relations

(1 − µ

)

dµ

=−nµP

+ (n + m)P

n−1

and

µP

n + m

2n + 1

n−1

n − m + 1

2n + 1

n+1

to prove the validity of equation (26.67).

Predictability

The convection equations in the form presented by Lorenz (1963) have been in-

vestigated very thoroughly because they exhibit chaotic behavior for a wide range

of values of model parameters. Lorenz discovered that his simple-looking three-

dimensional deterministic system yielded solutions that oscillate irregularly, never

exactly repeating but always remaining in a bounded region of phase space. This

aperiodic long-term behavior exhibits a very sensitive dependence on initial condi-

tions. Since the Lorenz system consists of nonlinear differential equations, he found

the trajectories describing the convection by numerical integration. By plotting the

trajectories in three dimensions, he discovered that they settled onto a very com-

plicated set, which is now called a strange attractor. The expression deterministic

system implies that the system has no random or noisy inputs or parameters. The

irregular behavior results from the nonlinear terms.

27.1 Derivation and discussion of the Lorenz equations

Lorenz obtained his mathematical system by drastically simplifying the convection

equations of Saltzman (1962) which describe convection rolls in the atmosphere.

We will now derive and discuss the Lorenz equations in some detail, beginning

with the basic model equations for two-dimensional ﬂow in the (x,z)-plane. We

apply the Boussinesq approximation by assuming that no divergence takes place

and that the rotation of the earth can be neglected. In the (x,z)-plane the velocity

vector v

, the gradient operator ∇

, the divergence D

, and the vorticity ζ

are

deﬁned by

= ui + wk, ∇

= i

∂

∂x

+ k

∂

∂z

∂u

∂x

∂w

∂z

,ζ

∂w

∂x

−

∂u

∂z

(27.1)

where the index v denotes the vertical direction. The equation of motion in this

669

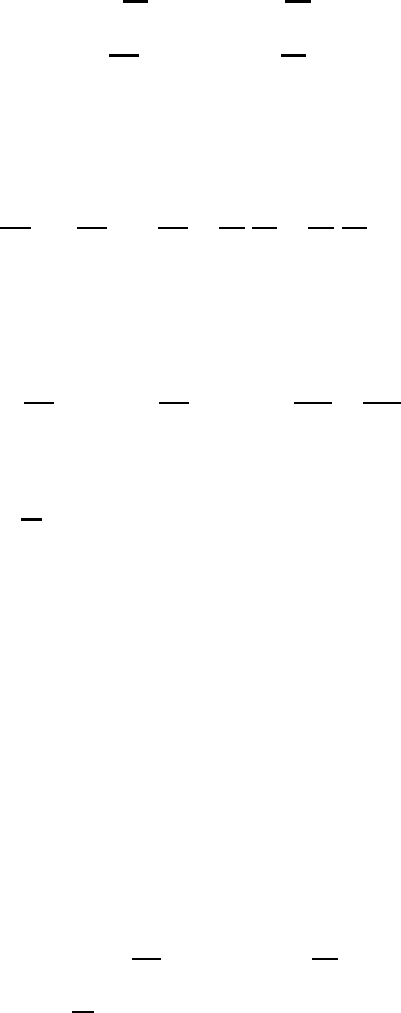
670 Predictability

plane is given by

(a)

∂u

∂t

+ v

·∇

u + α

∂p

∂x

− ν ∇

u = 0

(b)

∂w

∂t

+ v

·∇

w + α

∂p

∂z

− ν ∇

w = 0

(27.2)

where ν is the kinematic viscosity and α is the speciﬁc volume. By differentiating

(27.2a) and (27.2b) with respect to z and x, and subtracting one of the resulting

equations from the other, we obtain the vorticity equation

∂ζ

∂t

+ u

∂ζ

∂x

+ w

∂ζ

∂z

∂α

∂x

∂p

∂z

−

∂α

∂z

∂p

∂x

− ν ∇

= 0(27.3)

The rotational axis of the vorticity is orthogonal to the (x,z)-plane, thus pointing

in the y-direction. Since the divergence is assumed to be zero, the velocity ﬁeld

and the vorticity can be expressed in terms of the stream function ψ(x, z,t):

u =−

∂ψ

∂z

,w=

∂ψ

∂x

,ζ

∂

∂x

∂

∂z

=∇

ψ (27.4)

Thus the vorticity equation can also be written as

∂

∂t



∇



+ J



ψ, ∇



= J (α, −p) + ν ∇



∇



(27.5)

The Jacobian operator J (α, −p)isthesolenoidal term representing the number

of unit solenoids in the (x,z)-plane. The solenoids cause an acceleration of the

circulation driving the convection.

With Saltzman (1962), we make the following assumptions about the temperature

and the speciﬁc volume ﬁelds. The temperature distribution is expressed by

T (x,z, t) = T

(t) + T

(x,z, t)(27.6)

where T

(t) is a mean value over the entire convection region and T

(x,z, t)is

the deviation from the mean value. The anelastic assumption is assumed to apply,

so the relative temperature deviations are large in comparison with the relative

pressure variations. Therefore, the Taylor expansion of the speciﬁc volume α about

an equilibrium point (T

) can be approximated by

α(T,p) = α(T

) +

∂α

∂T



(T − T

) +

∂α

∂p



(p − p

) +···

≈ α

(T − T

) with α

= R

(27.7)