Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

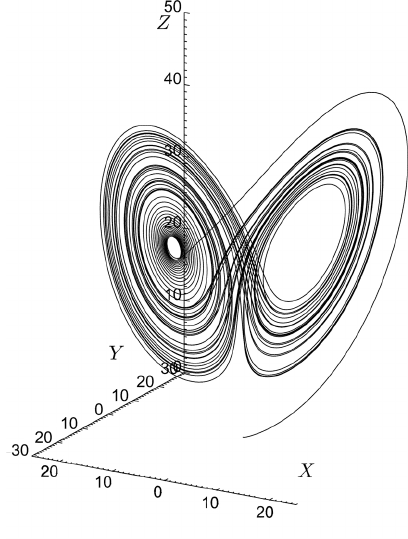
27.2 The effect of uncertainties in the initial conditions 681

−

Fig. 27.2 Aperiodic motion of the Lorenz system, showing trajectories in the (X,Y,Z)-

space.

may think of this small initial difference as simulating measurement errors, which

can never be avoided entirely. For nonchaotic systems this uncertainty in the initial

conditions leads to a prediction error that grows linearly with time. For chaotic

systems this error grows exponentially with time, so that, after a short time, the

state of the system is essentially unknown. This means that long-term prediction is

impossible for Lorenz-type systems.

27.2 The effect of uncertainties in the initial conditions

We wish to discuss the situation more quantitatively. Let the uncertainties in the

initial conditions be represented by two points on two neighboring trajectories.

Suppose that the transient has decayed so that the trajectory is already on the

attractor. Let X(t) represent a point on the attractor at time t. We consider a nearby

point X(t) +δ(t) on a neighboring trajectory, where δ(t) is a tiny separation vector

of initial length

; see Figure 27.4. Numerical studies of the Lorenz attractor

show that the separation vector changes approximately according to

δ(t) =

exp(λ

t),λ

≈ 0.9(27.46)

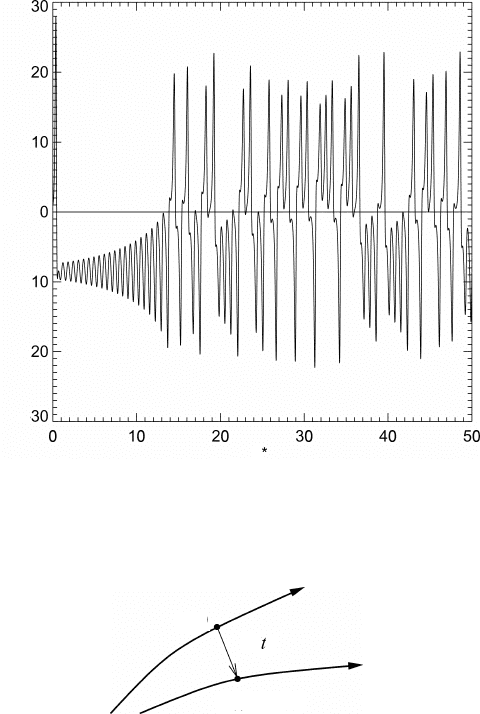
682 Predictability

−

Fig. 27.3 Aperiodic motion of the Lorenz system, showing the Y -component versus

dimensionless time t

∗

X(t)

( )

X(t) + δ(t)

Fig. 27.4 Two points in phase space on neighboring trajectories.

where λ

is the Liapunov exponent. Hence neighboring trajectories separate ex-

ponentially fast. Actually there are n different Liapunov exponents for an n-

dimensional system but λ

≈ 0.9 turns out to be the largest value. Whenever

a system has a positive Liapunov exponent, there is a time horizon beyond which

prediction breaks down. This is shown schematically in Figure 27.5. Beyond t = t

hor

the predictability breaks down. The two initial conditions represented by points on

the plot are so closely spaced that they cannot be distinguished.

Let us assume that the initial conditions of some physical experiment have been

determined very accurately. Nevertheless, a small measurement error will always

occur so that the measured initial condition differs from the true initial condition by

.Aftertimet of the prediction period the discrepancy has increased according

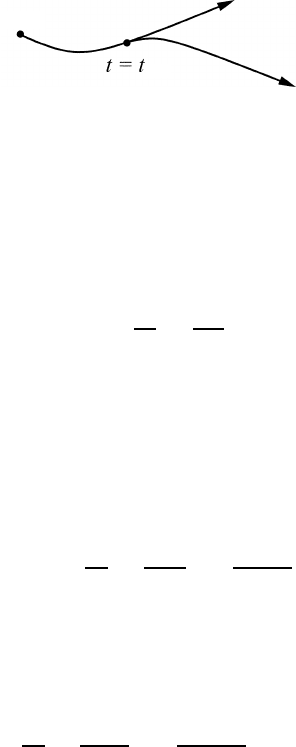
27.3 Limitations of deterministic predictability of the atmosphere 683

t = 0

hor

Fig. 27.5 A schematic plot of the time horizon where the two trajectories diverge rapidly.

to (27.46). We must permit a certain acceptable tolerance in the accuracy of the

prediction. Let a be a measure of this tolerance, i.e. if a prediction is within a of the

true state, then the prediction is tolerable. Thus the prediction becomes intolerable

δ(t)

≥ a. According to (27.46) the order of magnitude O of the time interval

hor

may be expressed as

hor

≈ O







(27.47)

Let us consider the following idealized example, which has little to do with

actual weather prediction. In a ﬁrst attempt, we are trying to predict a chaotic

system within a tolerance of a = 10

−3

, assuming that the initial state is uncertain

to within

= 10

−7

. For what time period can we predict the state of the system

and still remain within the given tolerance? In this case the time horizon is given

hor

(1) ≈



−3

−7



4ln10

(27.48)

In a second attempt we succeed in measuring the initial state a million times better

so that

= 10

−13

. How much longer can we predict within the tolerance limits?

The result is disappointing, as follows from

hor

(2) ≈



−3

−13



10 ln 10

= 2.5t

hor

(1) (27.49)

The conclusion is that a million-fold improvement in the initial uncertainty permits

us to predict for only 2.5 times longer. Lorenz suggested that this logarithmic

dependency on

is what makes long-term weather prediction so difﬁcult.

27.3 Limitations of deterministic predictability of the atmosphere

In the previous section we gave a rather artiﬁcial example of the Liapunov time

horizon of a chaotic system that is difﬁcult to apply to weather prediction. It is at

present not possible to state this time horizon in a general form since the time span

of predictability depends on the scale of the ﬁelds to be predicted and also on the

synoptic situation.

684 Predictability

Table 27.1. Spatial and time scales of atmospheric motion

Motion Spatial scale Time scale

Turbulence 0.1–100 m 1–1000 s

Convection 0.1–10 km 1–60 min

Mesoscale motion 1–1000 km 30 min to several days

Large-scale motion 1000–10 000 km 1–10 days

After and even before Lorenz (1963) published his celebrated paper, a number of

publications attempting to assess the predictability of the atmosphere appeared in

the literature. To a large extent, the prediction of the future state of the atmosphere

for an extended time period is very difﬁcult due to the width of the spectrum of

atmospheric processes. To give an impression of the scales of motion, we present in

Table 27.1 a very rough classiﬁcation of the spatial and time scales of atmospheric

motion.

More reﬁned classiﬁcations are avaliable, see e.g. Orlanski (1975). For large-

scale motion the characteristic scales are determined by the wavelength and the

period of the planetary waves. On smaller scales the dimensions and life times

of turbulent vortices determine the characteristic scales. Nonlinear interactions of

physical processes between different scales take place continually and vary strongly

in time and space.

Weather prediction on a mathematical–physical basis proceeds as follows. In

order to study weather phenomena of a certain scale, we must construct a math-

ematical model by employing the methods of scale analysis. The model is made

deterministic by parameterizing the interactions with neighboring scales in terms

of available model variables. Since a general parameterization theory is not yet

available, it is necessary to employ empirical knowledge to determine the pa-

rameter functions. This procedure introduces nondeterministic elements into the

prediction model. In order to develop a global circulation model, for example, it

would be necessary to parameterize the interactions with the complete spectrum

of the subsynoptic processes. So far this problem has not been solved satisfacto-

rily.

In order to carry out short- and medium-range numerical weather forecasts, it

is necessary to initialize the model with consistent input data in order to integrate

the predictive system of differential equations forward in time. The ﬁeld of the

initial data may be obtained with the help of an objective analyis. Procedures for

how to carry out this analysis are given by Haltiner and Williams (1980) and in

more recent references. Various sophisticated methods have been devised in or-

der to make the observed data physically and computationally as consistent with

27.3 Limitations of deterministic predictability of the atmosphere 685

the numerical model as possible. Methods have been proposed for producing an

objective analysis by statistically extracting the maximum amount of information

from observations, climatological data, spatial correlations between meteorological

variables, and other available data. This type of procedure, known as the optimum

interpolation, requires knowledge of the statistical structure of the ﬁelds of meteo-

rological variables. Nevertheless, upon completion of the objective analysis, mass

and motion ﬁelds are still not precisely balanced.

Naturally, questions about the sensitivity of the weather-prediction model arise

due to uncertainties in the parameterized interaction with neighboring scales, the

uncertainties in the initial conditions, and the particular properties of the numerical

scheme. In other words, for what prediction time interval is the deterministic

character of the model equations prevalent before the nondeterministic elements

begin to dominate the prediction? We can well imagine that there must be limitations

to deterministic predictability, which vary from one mathematical model to the next.

In the remaining part of this chapter we will investigate the uncertainties in the

initial conditions.

Among various attempts to investigate the predictability of the atmosphere,

Lorenz (1969) modeled the atmosphere with the help of the divergence-free

barotropic vorticity equation in which the horizontal velocity is expressed in terms

of the stream function. Assuming “exact” initial conditions and ignoring possible

errors due to the numerical procedure, the solution of this deterministic equation

should result in an “exact” deterministic prediction over an arbitrarily long period

of time. Exact initial conditions, however, do not exist, so the predicted ﬁelds

are expected to be at variance with nature after a certain time span. Moreover,

it should be realized that the model equations are too simple to approximate the

actual atmospheric behavior over an extended time period.

To simulate the effect of uncertainties in the initial conditions, two predictions

may be carried out. The ﬁrst prediction uses initial conditions that are deﬁned to

be exact. The prediction on the basis of the model equations is deterministic and

“exact,” thus correctly representing the nature of the model. The second prediction

uses somewhat different initial conditions, which simulate imperfect measurements

and other errors. After a longer prediction time the results differ so much that, even

on the largest scales, they are not even similar. In fact, Lorenz showed that, on the

basis of hardly discernible differences in the initial conditions of the subsynoptic

scales, but identical initial conditions in the synoptic scale, after three weeks of

prediction time the two forecasts were so different that they could not be compared

in a reasonable way. We may conclude from this numerical investigation that

the atmosphere has forgotten the initial conditions altogether after a time span

of no more than four weeks. The short memory of the atmosphere is caused by

the nonlinear interactions taking place, which are accompanied by a propagation

686 Predictability

of errors relative to the initial conditions. This memory property has been well

known for many years from the numerical experiments simulating the general

circulation. Even on starting the numerical integration with the simplest and most

unrealistic initial conditions, that is a resting atmosphere and isothermal vertical

temperature stratiﬁcation, due to an inﬂux of energy and to friction a reasonably

realistic atmosphere has evolved after a time span of only one month. Again,

this implies that the atmosphere has completely forgotten the unrealistic initial

conditions.

Proponents of the so-called stochastic dynamic method of weather prediction and

others have criticized the conclusions resulting from Lorenz’s numerical investi-

gation. They argued that the Lorenz model, ignoring even the important β effect,

is too simple to give a realistic estimate of the limits of atmospheric predictability.

The prediction range can be extended by applying the stochastic dynamic method

to the Lorenz scheme and to more complete prediction models. The stochastic

dynamic approach apparently was initiated by Obuchov (1967). Just like any other

dynamic prediction, the method is based on the deterministic model equations

generally used to describe the atmosphere. The novel part is that this method in-

troduces the concept of uncertainty in the initial conditions by means of statistical

characteristics.

Even if the initial conditions cannot be precisely known, from experience we

have developed some ideas about the most probable forms of the ﬁelds of variables

describing the initial state of the atmosphere. The typical operational forecast

requires one ﬁeld of initial data for each variable with unknown errors. Instead of

prescribing a single set of initial ﬁelds of the variables, one prescribes a set of initial

ﬁelds of variables by means of a probability distribution of initial ﬁelds. Instead of

a single forecast resulting from a single set of initial ﬁelds of the variables, a great

number of forecasts can be produced. How one might obtain an approximation of

the initial joint probability distribution will not be discussed here. For our purposes

we simply assume that it can be constructed in some way.

Any probability distribution may be characterized by the usual statistical mea-

sures: expectation, variance, and higher moments. Thus we may describe the joint

probability distribution of the initial ﬁelds of variables by these statistical measures.

Moreover, we may also calculate the same statistical measures from the collection

of the predicted ﬁelds. For various times and spatial points the statistical measures

of the predicted ﬁelds may be related to the corresponding measures of the initial

ﬁelds. The prediction of the statistical measures of the variables is the core of

the stochastic dynamic prediction. This forecasting procedure makes it possible to

extend the predictability horizon. By employing the barotropic vorticity equation

in the form used by Lorenz, it is possible to increase the duration of predictability

signiﬁcantly.

27.3 Limitations of deterministic predictability of the atmosphere 687

In the following we will give a brief mathematical description of the stochastic

dynamic method. Lorenz (1963) had already recognized that all meteorological

prediction equations, after transformation into the spectral domain, can be written

in the form



kmn

−



+ C

(27.50)

where the X

are general time-dependent variables describing the state of the

atmosphere. The time t is the only independent variable; A, B, C are constants

describing the nonlinear interaction, external forces, and dissipative mechanisms.

The symbols m and n are dummy indices. Fortak (1973) veriﬁed the form (27.50)

by employing the following ﬁve dependent variables: the three components of the

wind vector (u, v, w), the Exner function 6 = c

(p/p

)

p,0

, and the potential

temperature θ. By developing the ﬁve scalar variables in the form















m=1













,6=



m=1

,θ=



m=1

(27.51)

where F

= F

(x,y, z) is a suitable normalized three-dimensional orthogonal func-

tion, we obtain a set of ﬁve ordinary differential equations ( ˙u

, ˙v

, ˙w

)

of relatively simple structure.

In order to proceed with our discussion, we do not need to know the mathematical

form of the F

and need not repeat Fortak’s analysis. The functions F

may be

obtained in generalization to the two-dimensional case, see Abramowitz and Segun

(1968). Suppose, for example, that the spatial ﬁelds are resolved to a wavenumber

N = 20. In this case we would have to evaluate deterministically 5N = 100

nonlinear coupled time-dependent ordinary differential equations for the coefﬁcient

functions X

assuming the existence of exact initial conditions of the variables.

Imagining that this 5N-dimensional space is spanned by the totality of the variables

then the state of the system in phase space at a certain time is represented by a

point. As we have previously discussed, any changes in the state of this system are

represented by the motion of this point or by a trajectory in phase space.

We know that the initial conditions cannot be speciﬁed exactly. This is equiv-

alent to saying that we do not know the exact location of the point in phase

space specifying the initial state t = t

. Suppose that the probability density

P (X

,...,X

) for the position of the point is available with P>0forall

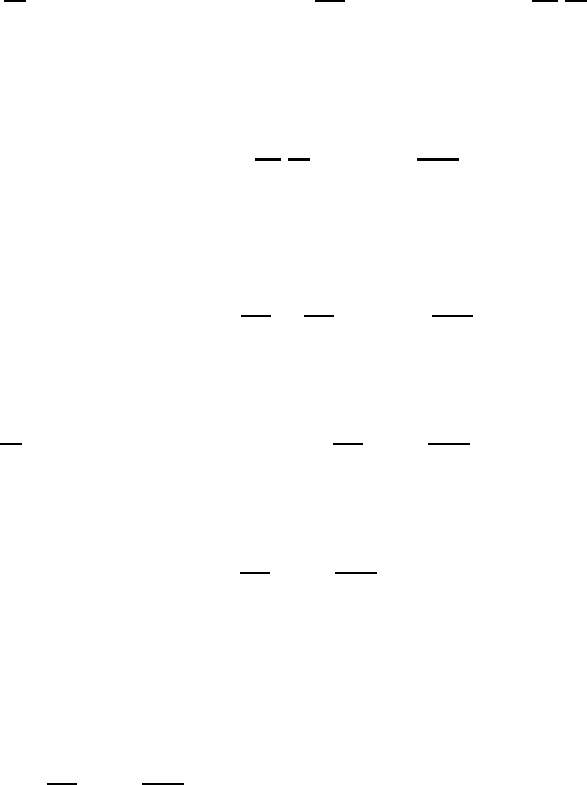
688 Predictability

and all t. By deﬁnition, the normalization condition



∞

−∞

···



P (X

,...,X

,t) dX

···dX



∞

−∞

···



P (X

,...,X

,t) dτ = 1

(27.52)

must be valid for all t. The evolution with time of the probability density follows

from the differentiation with respect to time of the normalization condition. By

employing Lagrange’s method we obtain





∞

−∞

···



Pdτ





∞

−∞

···



dτ +



∞

−∞

···





dτ

(dτ)



dτ = 0

(27.53)

The expression in parentheses on the right-hand side represents the relative change

in volume or the divergence:

dτ

(dτ) =



m=1

∂

∂X

(27.54)

which is a generalization of the three-dimensional case; see (M6.38b). Next we

replace dP /d t in (27.53) by the generalized Euler expansion

∂P

∂t



m=1

∂P

∂X

(27.55)

Substitution of this expression together with (27.54) into (27.53) yields





∞

−∞

···



Pdτ





∞

−∞

···





∂P

∂t



m=1

∂

∂X

)



dτ = 0(27.56)

In differential form this equation may be written as

∂P

∂t



m=1

∂

∂X

) = 0(27.57)

which is known as the Liouville equation or the continuity equation for the proba-

bility density.

Equation (27.57) can be evaluated, at least in principle, if we replace

(27.50). This results in

∂P

∂t



m=1

∂

∂X





r=1



s=1

mrs

−



r=1

+ C



= 0(27.58)

27.4 Basic equations of the approximate stochastic dynamic method 689

which describes the evolution with time of the probability density for a speciﬁc me-

teorological problem as formulated by a model. The latter equation was originally

and independently derived by Epstein (1969) and by Tatarsky (1969). In principle,

this equation can be solved numerically if P (t = t

) is known and if the boundary

conditions for P (vanishing at inﬁnity) can be satisﬁed.

At present the numerical effort required in order to solve (27.58) is prohibitively

expensive and practically impossible. Tatarsky and Epstein pointed out that com-

plete knowledge of P includes much superﬂuous information. So it is usually

sufﬁcient to know the simplest moments describing essential characteristics of the

distribution instead of knowing the complete distribution. These are the ﬁrst and the

second moment. The ﬁrst moment is the expectation or mean value of the variable

while the second moment is related to the covariance. Knowledge of these two

statistical measures is sufﬁcient for approximating the actual probability density

by the Gaussian distribution.

27.4 Basic equations of the approximate stochastic dynamic method

We will now derive the prognostic equations for the expectation value and for

the covariance tensor. These equations were given independently by Tatarsky and

Epstein. It turns out that we will have to deal with the same type of closure problem

as that which is known to us from the theory of turbulence.

The ﬁrst moment or the expectation value of X, also known as the mean value

,isdeﬁnedby

E(X

) = µ



∞

−∞

···



P (X

,...,X

,t) dτ (27.59)

The second moment ρ

is given by

(t) =



∞

−∞

···



P (X

,...,X

,t) dτ (27.60)

This quantity is related to the covariance σ

as will be shown next. In analogy to

the theory of turbulence, we split the variable X

into the mean value µ

plus the

deviation X



= µ

+ X



with E(X



) = 0(27.61)

By deﬁnition, the expectation value of the deviation X



is zero. Equation (27.60)

involves the product X

. By introducing (27.61) into this product we ﬁnd

= µ

+ X



+ X



+ X



(27.62)

690 Predictability

On applying the expectation operator to (27.62) we immediately ﬁnd

E(X

) = µ

+ σ

with σ

= E(X



)(27.63)

Since E(X

) = ρ

we have found the relation between the second moment

and the covariance. The expectation value of a function is deﬁned analogously to

(27.59) simply by replacing X

by the function f (X

,...,X

Of primary importance to stochastic dynamic forecasting is the time derivative

of the expectation value. With the help of the Liouville equation (27.57) it is not

very difﬁcult to prove the validity of

[E(f )] = E





(27.64)

showing that the mathematical expectation operator and the time derivative may

be interchanged. We will leave the proof to the exercises.

To ﬁnd the prognostic equation of the mean value µ

we ﬁrst apply the expecta-

tion operator to equation (27.50) and obtain







m=1



n=1

kmn

E(X

) −



m=1

E(X

) + C

E(1) (27.65)

With the help of (27.63) and (27.64) it is not difﬁcult to obtain the desired equation

˙µ



m=1



n=1

kmn

−



m=1

+ C



m=1



n=1

kmn

(27.66)

Comparison of (27.66) with (27.50) shows the similarity between these two equa-

tions. The ﬁrst three terms are identical in form. In place of X

in (27.50) we now

have the mean value µ

. The decisive difﬁculty with equation (27.66) arises from

the last term, which requires knowledge of the covariance σ

. Thus we need to

derive a prognostic equation for the covariance. If there were no uncertainties, the

covariance tensor σ

would be zero and the ﬁnal term would vanish so that there

would be no need to obtain a prognostic equation for σ

. In practical situations this

idealized case of zero uncertainties does not occur. The analogy with averaging

the equation of motion is apparent since the averaging procedure produces the

Reynolds stress tensor as an additional term.

Now we direct our attention to the evaluation of the covariance term in (27.66).

There is no formal difﬁculty in ﬁnding the prognostic equation for σ

. All we need

to do is to differentiate (27.63) with respect to time, yielding

˙σ

= E(

) + E(X

) − ˙µ

− µ

˙µ

(27.67)