Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

23.6 The geostrophic approximation of the heat equation 601

(i) Assuming the validity of the hydrostatic equation, it is shown in textbooks on thermo-

dynamics that the internal and the potential energy in an air column always change

in the same sense. Thus, for a qualitative discussion we do not need to consider the

internal energy separately.

(ii) In case of an atmospheric development the average kinetic energy in region A must

increase. This occurs at the expense of the potential and the internal energy. Owing

to the rising warm air and the sinking cold air, the center of mass of the system must

decrease in height. At the end of this section we will verify mathematically that the

negative correlation

Tω < 0 is consistent with an increase of the average kinetic

energy.

From the correlations (23.24) we conclude that, in the developing stage of region

A in the upper and in the lower section, the two terms on the right-hand side of

(23.23a) have opposite effects. The term

TD results in heating of the upper section

(p<p

lnd

) and cooling of the lower section of the atmosphere. Owing to the thermal

rearrangement, we conclude from equations (23.23a) and (23.24) that



(23.25)

Owing to the geostrophic approximation, in the averaged ﬁltered equation

(23.23b) the term

TD has disappeared. Since (p/R)σ

ω has an effect opposite

to that of (p/R)σ

ω + TD, it then follows from (23.23a) and (23.23b) that the

changes in temperature in the ﬁltered and unﬁltered systems take place in opposite

directions.

In order to improve the energy balance of the ﬁltered system, it seems logical to

omit not only

TD in order to preserve integral properties, but also the less effective

term (p/R)σ

ω in (23.23b). This term drops out on replacing the static stability

(x,y, p, t)byanaveragevalueσ

(p, t), so

ω = σ

ω = 0(23.26)

This is the reason why

was introduced into equation (23.19). Owing to this

treatment the energy balance will certainly not be corrected but now the unphysical

simultaneous increase of potential and kinetic energy is no longer possible.

We now want to show that the average kinetic energy in the developing region

does indeed increase with time as required by the correlation product (23.24).

We ﬁrst obtain a prognostic equation for the kinetic energy of horizontal motion

= v

/2. In vector form the horizontal equation of motion is given by

∂v

∂t

+ v

·∇

+ ω

∂v

∂p

+ f k × v

=−∇

φ (23.27)

602 A quasi-geostrophic baroclinic model

Scalar multiplication of this equation by the horizontal velocity v

results in

∂K

∂t

+ v

·∇

+ ω

∂K

∂p

=−v

·∇

φ (23.28)

Owing to the continuity equation (22.23) we ﬁnd the equivalent form

∂K

∂t

+∇

· (v

) +

∂

∂p

(ωK

) =−∇

· (v

φ) + φ ∇

· v

(23.29)

Since we are dealing with a developing region that is assumed to extend from the

bottom to the top of the model atmosphere, we are motivated to introduce a volume

average by means of



Bdxdydp (23.30)

Here B, as before, represents an arbitrary ﬁeld function. The normal velocity van-

ishes at the boundaries of V since we are dealing with a closed system. Application

of (23.30) to (23.29) immediately yields

∂

∂t

φ ∇

· v

(23.31)

Here we have used (23.22b) and the lower and upper boundary conditions with

ω = 0atp = 0andp = p

. With the help of the continuity equation and with

(23.8), the right-hand side of (23.31) can easily be rewritten as

φ ∇

· v

=−

∂

∂p

(ωφ)

+ ω

∂φ

∂p

=−R

Tω

(23.32)

so the volume average of the kinetic energy may be stated in the form

∂

∂t

=−R

Tω

(23.33)

Hence, if we require an increase in the kinetic energy

, the vertical velocity and

the temperature T must be negatively correlated everywhere in the atmosphere.

Reference to (23.24) shows that this requirement is precisely satisﬁed.

23.7 The geostrophic approximation of the vorticity equation 603

23.7 The geostrophic approximation of the vorticity equation

In this section we derive a simpliﬁed form of the vorticity equation, which will

be used in the quasi-geostrophic system. To begin with, we rewrite the baroclinic

vorticity equation (23.10) by replacing the divergence term with the help of the

continuity equation,

∂ζ

∂t

+ v

·∇

η + ω

∂ζ

∂p

+ k ·



∇

ω ×

∂v

∂p



= η

∂ω

∂p

(23.34)

which may also be written in the equivalent form

∂ζ

∂t

+∇



ηv

+ ω

∂v

∂p

× k



= 0(23.35)

Thus, the tendency of the vorticity can be expressed as the divergence of two

vectors. We wish to retain this form in the quasi-geostrophic theory. In analogy to

(23.34) the selective geostrophic approximation of the vorticity equation can be

written as

∂ζ

∂t

+ v

·∇

+ ω

∂ζ

∂p

+ k ·



∇

ω ×

∂v

∂p



= η

∂ω

∂p

(23.36)

It should be observed that ∂ω/∂p appearing on the right-hand side of this equation

is equivalent to −∇ · v

, so the actual horizontal wind velocity is retained in this

term while everywhere else it is replaced by the geostrophic wind. This is the

reason why we speak of a selective geostrophic approximation.

We will now discuss the selective or quasi-geostrophic approximation of the vor-

ticity equation. According to (23.22b) there exists the following integral property

for the unﬁltered system:

∇

· (ηv

) = v

·∇

η + η ∇

· v

= 0(23.37)

We wish to retain this integral property even after the introduction of the geostrophic

approximation

·∇

η → v

·∇

, η ∇

· v

→−η

∂ω

∂p

(23.38)

While the ﬁrst expression of (23.38) is already zero since

·∇

= ∇

· (v

) =

0, the second expression does not vanish. However, this expression will also be

zero if we replace η

by a constant value. To preserve the integral property (23.37)

in the ﬁltered system, we neglect ζ

in the expression for the absolute geostrophic

vorticity η

= ζ

+ f and replace f by the constant Coriolis parameter f

. Under

604 A quasi-geostrophic baroclinic model

typical midlatitude atmospheric conditions ζ

<f. Now we obtain for the second

expression of (23.38)

η ∇

· v

→−η

∂ω

∂p

=−

(ζ

+ f )

∂ω

∂p

≈−

∂ω

∂p

= f

∇

· v

= 0(23.39)

Hence, we also retain the integral property (23.37) in the ﬁltered system.

Owing to the approximation (23.39) the term ζ

∂ω/∂p will be ignored on the

right-hand side of (23.36). Let us now investigate the importance of the term

ω∂ζ

/∂p. Introducing the vertical average over the model atmosphere according



Bdp (23.40)

we obtain

∂

∂p

(ωζ

)



∂

∂p

(ωζ

) dp = 0(23.41)

since the vertical velocity vanishes at the boundaries of the atmosphere. As a

consequence of this we have



∂ζ

∂p



∂ω

∂p



(23.42)

Hence, on average, the term ω∂ζ

/∂p is of the same order of magnitude as the

term ζ

∂ω/∂p. Since the term ζ

∂ω/∂p has been neglected in (23.36), it seems

logical to ignore the term ω∂ζ

/∂p on the left-hand side of this equation as well.

Finally we observe that the term ω∂ζ

/∂p plus the twisting term can be combined

to give a divergence expression:

∂ζ

∂p

+ k ·



∇

ω ×

∂v

∂p



=∇



∂v

∂p

× k



(23.43)

Obviously, without the omitted term we cannot obtain a divergence expression

for the tendency of the geostrophic vorticity. Thus, it stands to reason that we

should omit the twisting term in (23.36) as well. This simpliﬁcation is also justiﬁed

because, in large-scale ﬂow ﬁelds, ∇

ω is usually small in comparison with the

remaining terms of the vorticity equation.

On introducing these simpliﬁcations into (23.36) we obtain the quasi-geostrophic

approximation of the vorticity equation as

∂ζ

∂t

+ v

·∇

= f

∂ω

∂p

(23.44)

23.8 The ω equation 605

which, in analogy to (23.35), can be written in the desired divergence form

∂ζ

∂t

+∇

· (η

+ f

) = 0(23.45)

Utilizing (23.17) and (23.18), we may also write (23.44) as

∂

∂t



∇





φ,∇



+ β

∂φ

∂x

= f

∂ω

∂p

(23.46)

In order to give a simple physical interpretion of the vorticity equation, we

integrate (23.44) over the depth of the atmosphere from p = 0top = p

Observing that the generalized vertical velocity vanishes at the lower and the upper

boundaries of the model, we obtain the following tendency equation:

∂

∂t

=−v

·∇

(ζ

+ f )

(23.47)

This equation shows that, within the validity of the quasi-geostrophic theory, the

change with time of the vertical average of the geostrophic vorticity in the p system

depends solely on the horizontal advection of the absolute vorticity. A more detailed

physical interpretation will be given later.

It should be realized that the derivation of the divergence form of the vorticity

equation in the geostrophic approximation results in a severe reduction of physical

signiﬁcance in comparison with the original equation. We will show at the end of

this chapter that the quasi-geostrophic approximation of the vorticity equation and

other results of the quasi-geostrophic theory can be easily derived with the help of

the ageostrophic wind approximation of Philipps (1939).

The heat equation (23.19) and the geostrophic vorticity equation (23.44) form

the basis of the entire quasi-geostrophic theory. Both equations result from a drastic

simpliﬁcation of the original equations. In particular, the geostrophic approxima-

tions of the horizontal wind in the advection terms v

·∇

T and v

·∇

η make

it impossible to realistically predict such processes as occlusion and frontogene-

sis and to form precise energy balances. However, it is possible to improve the

theory.

23.8 The ω equation

The heat equation, the vorticity equation, and the divergence equation require

knowledge of the vertical velocity ω. The integration of the continuity equation in

606 A quasi-geostrophic baroclinic model

the p system appears to give the required information:

ω =−



∇

· v

dp (23.48)

However, routine measurements of the horizontal wind ﬁeld are not sufﬁciently

accurate to determine the divergence ∇

· v

, so this equation is unsuitable for

ﬁnding ω. Thus, we have to look for a more powerful method to determine ω.

We proceed by eliminating the tendency ∂φ/∂t from the vorticity equation

(23.46) and from the heat equation in the form (23.19). This is accomplished by

the following mathematical operations. (1) We differentiate the vorticity equation

with respect to p. (2) We apply the horizontal Laplacian to the heat equation.

(3) We subtract one of the resulting equations from the other and ﬁnd

∇

ω + f

∂

∂p

∂

∂p





φ,

∇



+ β

∂

∂x ∂p

−

∇





φ,

∂φ

∂p



= f

∂

∂p

·∇

) −∇



·∇

∂φ

∂p



(23.49)

This equation is known as the ω equation. For large-scale motion the stability

function

> 0, so we are dealing with a partial differential equation of the el-

liptic type. Thus, we are confronted with a boundary-value problem permitting

us to ﬁnd ω if the geopotential ﬁeld φ(x,y, p, t = constant) is known at a ﬁxed

time. Textbooks on numerical analysis discuss the numerical procedures to be

used. In earlier days this equation closed a gap in routine weather observations,

which even today do not report the vertical velocity ﬁeld. The mass ﬁeld, repre-

sented by the geopotential, is measured relatively accurately. It is a simple matter

to ﬁnd the geostrophic wind from the geopotential ﬁeld, but it requires quite a

bit of numerical work to ﬁnd the generalized vertical velocity from the ω equa-

tion. Sometimes the ω equation is called the geostrophic relation for the vertical

wind.

It should be observed that the so-called τ equation is equivalent to the ω equation.

By eliminating ω from the vorticity and the heat equation we ﬁnd a second-

order partial differential equation for the tendency ∂φ/∂t, which for simplicity is

designated τ. Since we do not gain anything new, we omit a discussion of this

boundary-value problem.

The principle of the numerical solution for the quasi-geostrophic system will

now be summarized.

(i) At the initial time t

= 0, the geopotential φ(x, y,p,t

= 0) is assumed to be given

so that v

and ω can be determined by solving (23.17) and (23.49).

23.8 The ω equation 607

(ii) With ω known initially, a new φ-ﬁeld at t

= t

+ )t can be determined from the

vorticity equation (23.46). The whole system can now be iterated.

(iii) If the temperature ﬁeld is required at any time t, we have to solve the hydrostatic

equation (23.8).

(iv) If it is sufﬁcient to ﬁnd the actual wind ﬁeld in some approximation, we make use of

the divergence equation (23.13). By assuming that the divergence D is zero, we obtain

a balance equation of the Monge–Amp

ere type, which can be solved numerically. The

problem may be further simpliﬁed by assuming that barotropic conditions apply for

each layer so that ∂v

/∂p vanishes. Since the divergence was set equal to zero, we

may express the wind by means of the stream function. Thus, we have to solve the

following equation:



∂ψ

∂x

∂ψ

∂y



+∇

·(f ∇

ψ) =∇

φ with ∇

·(f ∇

ψ) =−βu+fζ (23.50)

We have shown that the quasi-geostrophic theory of ﬁltering has reduced the

prognostic system to a one-ﬁeld system. The entire prognostic process is reduced

to the determination of the geopotential ﬁeld, which must be known at the initial

time t

= 0. This fact veriﬁes that all noise waves (horizontal sound waves,

gravitational waves, inertial waves) have been eliminated, since they can appear

only if more than one variable can be speciﬁed without restriction at the initial time

= 0. In the next chapter we will actually show how to solve the quasi-geostrophic

system for the simple case of a four-layer model. It should be realized that, with the

availability of modern computers, the quasi-geostrophic theory is no longer used

for actual weather forecasting. Nevertheless, the theory is of great value for the

interpretation of the atmospheric mechanism.

In order to improve our understanding of the quasi-geostrophic theory we will

extract the physical content of the ω equation. In a rough approximation we assume

that the vertical velocity is given by a harmonic function of the form

ω = A sin



πp



cos(k

x)cos(k

y)(23.51)

satisfying the boundary conditions ω(p = 0) = ω(p = p

) = 0. Substituting

(23.51) into (23.49) yields

−l

ω = f

∂

∂p

·∇

) −∇



·∇

∂φ

∂p



(23.52)

where the correlation factor l

is given by

= f





+ σ



+ k



(23.53)

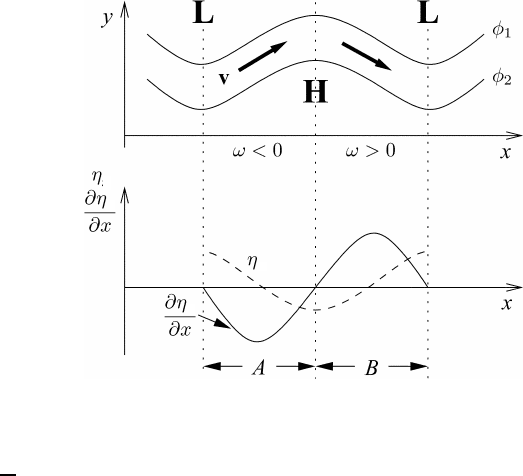
608 A quasi-geostrophic baroclinic model

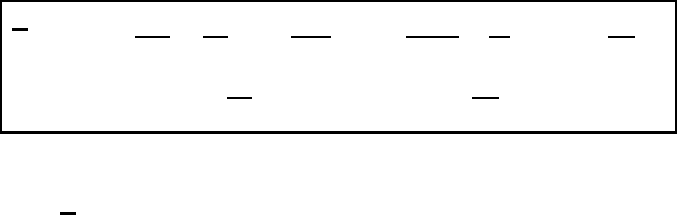
Fig. 23.4 A schematic intepretation of the term ∂(v

·∇

)/∂p of the ω equation.

Since σ

> 0 in large-scale motion, the quantity l

is positive. From (23.52) we

see that the left-hand side of (23.49) is negatively correlated to ω.

We will now interpret this equation. Since in the quasi-geostrophic theory we

have reduced the solution of the prognostic system to knowledge of the geopotential

ﬁeld, for the interpretation of the ω equation it is sufﬁcient to prescribe the φ-ﬁeld.

In order to understand the effect of the ﬁrst term on the right-hand side of (23.52),

let us consider an idealized sinusoidal pattern of φ-contour lines as shown in

the upper part of Figure 23.4. Since η

= (1/f

) ∇

φ + f the corresponding η

curve has maximum and minimum values in the low- and high-pressure regions,

respectively, as indicated by the dashed curve in the lower part of Figure 23.4. For

simplicity the lower part of Figure 23.4 depicts the evolution of the curves along

the x-axis only. From the η

curve we immediately obtain the ∇

curve which

is also shown in Figure 23.4. We conclude that, in region A of Figure 23.4, the

term v

·∇

< 0. For typical atmospheric situations |v

| increases with height

so that ∂(v

·∇

)/∂z < 0 and, therefore, ∂(v

·∇

)/∂p > 0. Hence, in region

A the ﬁrst term on the right-hand side of (23.52) induces rising air motion, that is

ω<0. In region B we observe the opposite situation. Here v

·∇

> 0sothat

∂(v

·∇

)/∂p < 0andω>0, thus indicating sinking air motion.

Next we consider the effect of the second term on the right-hand side of the ω

equation. An assumed vertical distribution of the geopotential ﬁeld is shown in the

upper part of Figure 23.5. Since ∂φ/∂p =−R

T/p we obtain regions of cold and

warm air as indicated in the ﬁgure. This yields cold- and warm-air advection in

regions A and B, respectively. From the given φ distribution we obtain curve a

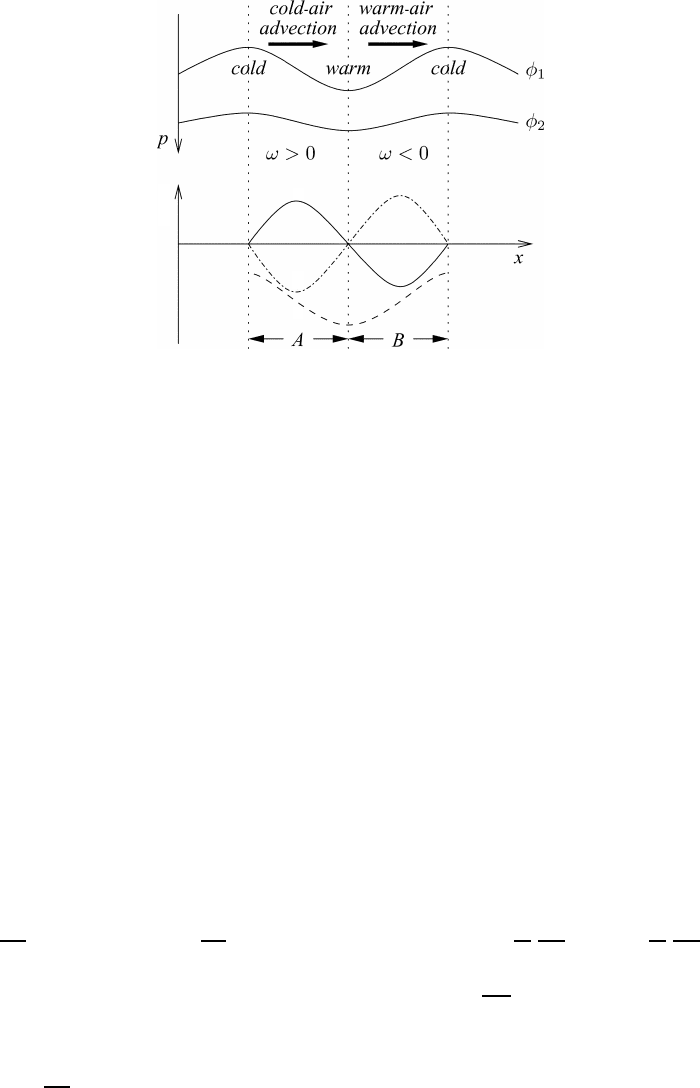
23.9 The Philipps approximation of the ageostrophic component 609

Fig. 23.5 A schematic intepretation of the term ∇

·∇

(∂φ/∂p)) of the ω equation.

The three curves in the lower part of the ﬁgure describe the pattern of the following terms:

a, ∂φ/∂p;b,v

·∇

(∂φ/∂p); and c, ∇

·∇

(∂φ/∂p)).

denoting the pattern of ∂φ/∂p. Curve b describes v

·∇

(∂φ/∂p) and ﬁnally the

pattern of the term ∇

·∇

(∂φ/∂p)] is indicated by curve c. According to (23.52)

we conclude that sinking air motion is observed in regions of cold-air advection

and rising air motion in regions of warm-air advection.

23.9 The Philipps approximation of the ageostrophic component

of the horizontal wind

The actual weather is determined in large measure by the deviation of the actual

horizontal wind from the geostrophic wind. We call this part of the horizontal

wind the ageostrophic wind component, v

= v

− v

. The ageostrophic wind

component can be elegantly discussed with the help of an approximation introduced

by Philipps (1939). Moreover, this approximation can be used to obtain most easily

the geostrophic approximation of the vorticity equation.

We begin the analysis by introducing the geostrophic wind into the horizontal

equation of motion (22.22), yielding

= f (v − v

=−f (u − u

) with u

=−

∂φ

∂y

∂φ

∂x

(23.54)

On multiplying the prognostic equation for v by i =

√

−1 and adding this to the

prognostic equation for u,weﬁnd

+ if q = if q

, with q = u + iv, q

= u

+ iv

(23.55)

610 A quasi-geostrophic baroclinic model

In this expression we approximate the Coriolis parameter f by the constant value

and obtain

q = q

g,0

−

with q

g,0

= u

g,0

+ iv

g,0

(23.56)

This rough approximation will be partly amended a little later. Successive differ-

entiation of (23.56) with respect to time yields

g,0

−

g,0

−

, ... (23.57)

On substituting these expressions into (23.56) we obtain the series

q = q

g,0

−

g,0

(if

)

g,0

−

(if

)

g,0

+ ···

∞



n=0

(−if

)

−n

g,0

(23.58)

For the convergence properties of this series, see the original paper of Philipps

(1939). If the series is discontinued after the second term we obtain the scalar form

of the wind equation:

u = u

g,0

−

g,0

,v= v

g,0

(23.59)

For brevity we write the vector form

= v

g,0

k ×

g,0

(23.60)

This equation expresses the actual wind by means of the approximated geostrophic

wind

g,0

k ×∇

φ =

(23.61)

and its time derivative. Writing the Coriolis parameter f in the form f = f

+)f

with )f  f

, the factor f

/f can be approximated as

= 1 −

≈ 1 −

= 2 −

(23.62)

From (23.61) we then obtain



2 −



g,0

(23.63)