Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

23
A quasi-geostrophic baroclinic model
23.1 Introduction
So far we have treated the so-called primitive equations of baroclinic systems
which, in addition to typical meteorological effects, automatically include horizon-
tally propagating sound waves as well as external and internal gravity waves. These
waves produce high-frequency oscillations in the numerical solutions of the baro-
clinic systems, which are of no interest to the meteorologist. Thus, the tendencies
of the various field variables are representative only of small time intervals of the
order of minutes while the predicted weather tendencies should be representative
of much longer time intervals.
In order to obtain meteorologically significant tendencies we are going to elim-
inate the meteorological noise from the primitive equations b y modifying the
predictive system so that a longer time step in the numerical solution becomes
possible. We recall that the vertically propagating sound waves are no longer a
part of the solution since they are removed by the hydrostatic approximation. The
noise filtering is accomplished by a diagnostic coupling of the horizontal wind field
and the mass field while in reality at a given time these fields are independent of
each other. The simplest coupling of the wind and mass field is the geostrophic
wind relation. The mathematical systems resulting from the artificial inclusion of
filter conditions are called quasi-geostrophic systems or, more generally, filtered
systems. For such systems at the initial time t
0
= 0 only one variable, usually the
geopotential, is specified without any restriction. The remaining dependent vari-
ables, for a given time, result from the employment of compatibility conditions
with the geopotential, which is known as diagnostic coupling.
For reasons of expediency we select the p system. Since we are interested only in
a qualitative discussion of the large-scale motion rather than in actual weather fore-
casts, we simply describe the flow on the tangential plane by setting the map factor
m
0
= 1. This eliminates a number of terms and simplifies our work. The theory
591
592 A quasi-geostrophic baroclinic model
which will be presented in the following sections is indispensable for compre-
hending in some depth large-scale atmospheric motion and some of the problems
associated with weather prediction. The actual weather prediction is carried out with
the help of the primitive equations in some modification using adjusted and com-
patible initial fields. In contrast to this, some drastic modifications are required in
order to obtain the quasi-geostrophic system. However, the advantage of the quasi-
geostrophic system is that the resulting mathematical system is simple enough to
promote the physical interpretation of the motion field. Moreover, we learn that
approximations have to be applied with great care, otherwise inconsistencies may
result, such as increases of the potential and kinetic energy at the same time.
We will now introduce and discuss in some detail the quasi-gestrophic theory,
which is based on suitable modifications of the first law of thermodynamics and
of the baroclinic vorticity equation. It will also be shown that the ageostrophic
approximation of the wind field due to Philipps (1939) is a very useful tool for
verifying some of the results of this theory. Numerous authors have contributed
to the development of the quasi-geostrophic theory. The first group of important
contributions includes the pioneering work of Charney (1947), Eady (1949), and
Phillips (1956).
23.2 The first law of thermodynamics in various forms
We begin our work by writing the heat equation in the form
ρc
p
dT
dt
−
dp
dt
= ρ
d
q
dt
(23.1)
where the term ρd
q/dt includes all heat sources such as radiation, heat conduction,
turbulent heat transport, phase changes of the water substance, and friction if the
equations to be considered represent the mean atmospheric motion. This equation
may also be expressed in terms of the potential temperature as
d ln θ
dt
=
1
c
p
T
d
q
dt
(23.2)
It is customary to introduce the static stability σ
0
which, according to (16.30), is
given by
σ
0
=−
1
ρ
∂ ln θ
∂p
=
R
0
p
R
0
T
c
p
p
−
∂T
∂p
=
R
2
0
T
gp
2
( − γ )(23.3)
Here and γ are, respectively, the dry adiabatic and the actually observed geo-
metric lapse rates. Expansion of (23.1) gives the form
∂T
∂t
+ v
h
·∇
h
T + ω
∂T
∂p
−
R
0
T
c
p
p
=
1
c
p
d q
dt
(23.4)
23.4 The vorticity and the divergence equation 593
from which it follows that
∂T
∂t
+ v
h
·∇
h
T −
pσ
0
ω
R
0
=
1
c
p
d q
dt
(23.5)
due to the introduction of the static stability by means of (23.3). Expanding (23.2)
results in
∂ ln θ
∂t
+ v
h
·∇
h
ln θ + ω
∂ ln θ
∂p
=
1
c
p
T
d
q
dt
(23.6)
or, using the static stability, we find
∂ ln θ
∂t
+ v
h
·∇
h
ln θ − ρσ
0
ω =
1
c
p
T
d
q
dt
(23.7)
Finally, we will write the heat equation in a form involving the geopotential φ.
From the hydrostatic equation we first find
∂φ
∂p
=−
1
ρ
=−
R
0
T
p
=⇒ T =−
p
R
0
∂φ
∂p
(23.8)
Remembering that all equations refer to the p system, we obtain from (23.5) after
a few easy steps the expression
∂
∂t
∂φ
∂p
+ v
h
·∇
h
∂φ
∂p
+ σ
0
ω =−
R
0
c
p
p
d q
dt
with σ
0
=
∂
2
φ
∂p
2
+
c
v
c
p
p
∂φ
∂p
(23.9)
The latter form of σ
0
follows from substituting (23.8) into (23.3) with R
0
= c
p
−c
v
.
The physical interpretation of the heat equation is quite simple. The first term
of equation (23.5) describes the temperature tendency, the second term expresses
the change in temperature due to horizontal advection, and the third term describes
convective processes or changes in temperature due to anisobaric vertical motion.
The term d
q/dt has already been explained above. Corresponding explanations
apply to equations (23.7) and (23.9).
23.4 The vorticity and the divergence equation
In order to eliminate the meteorological noise, it is convenient to employ the
baroclinic vorticity equation instead of the horizontal equation of motion itself.
The vorticity equation is a scalar equation and, therefore, cannot be equivalent to
the horizontal equation of motion, which is a vector equation. To express complete
equivalence to the equation of horizontal motion we must also add the baroclinic
divergence equation. A comparison of the filtered system with the exact system is
facilitated by applying the unfiltered vorticity and divergence equations instead of
employing the equivalent equation of horizontal motion itself.

594 A quasi-geostrophic baroclinic model
To begin with, we repeat the baroclinic vorticity equation (10.77) for the p
system, which, in its modified form, is one of the basic equations of the quasi-
geostrophic theory. Suppressing for convenience the suffix p and using the conti-
nuity equation (22.23), we find
∂η
∂t
+v
h
·∇
h
η +η ∇
h
· v
h
+ω
∂η
∂p
+k ·
∇
h
ω ×
∂v
h
∂p
= 0
I II III IV V
(23.10)
where η = k ·∇
h
×v
h
+ f is the absolute vorticity. This is the baroclinic vorticity
equation in the unfiltered form. Terms I, II, III, and IV can be easily interpreted but
term V is more difficult to comprehend. Term I stands for the local change of either
the absolute or the relative vorticity, term II represents the horizontal advection
of the absolute vorticity, term III describes the divergence or convergence of the
horizontal velocity, and convective processes are expressed by term IV. The twisting
term V, also called the tipping or the tilting term, implies that, due to rotational
motion, the vertical component of the vector ∇×v, i.e. the relative vorticity
ζ = k ·∇×v = k ·∇
h
×v
h
, increases at the expense of the horizontal component
of the vector ∇×v which is represented by the vertical shear k × ∂v/∂p.
The expansion of the twisting term results in
k ·
∇
h
ω ×
∂v
h
∂p
=
∂ω
∂x
∂v
∂p
−
∂ω
∂y
∂u
∂p
(23.11)
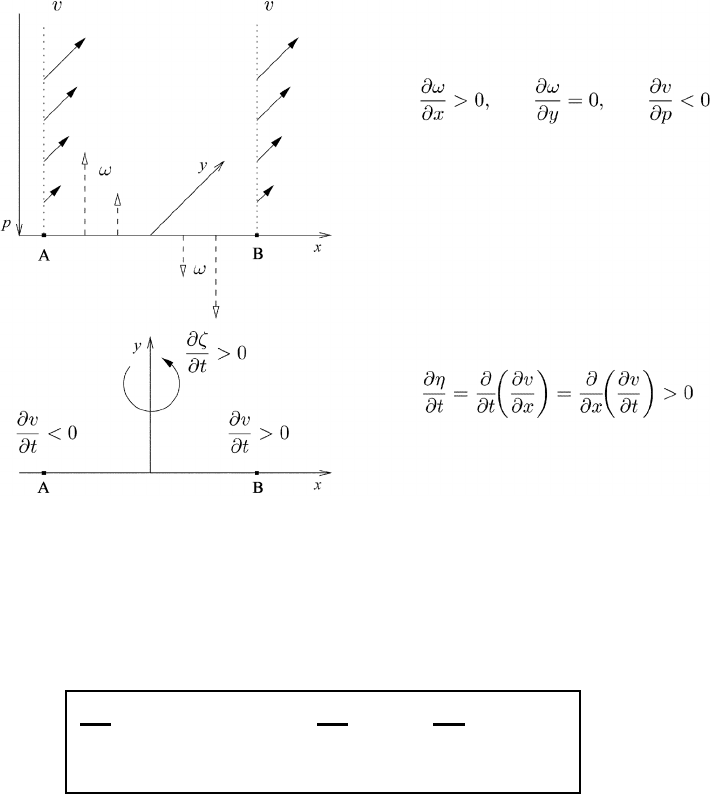
In order to better understand the meteorological significance of the twisting term,
we will consider the simplified physical situation shown in the upper part of
Figure 23.1. At the point A the upward transport of low v values from lower layers
will produce a local decrease of v with time, whereas at point B high v values of
upper layers are transported downward, yielding a local increase of v with time.
From (23.10) and (23.11) we see that, in this particular situation, the local change
with time of the vorticity resulting from the twisting term is positive, as indicated
in the lower part of the figure.
The baroclinic divergence equation, which is not yet at our disposal, will now be
derived. For the barotropic system the divergence equation (15.63) was obtained
from the horizontal equation of motion (15.21). The baroclinic form of the hori-
zontal equation of motion in the p system formally differs from (15.21) only by
virtue of the vertical advection term ω∂/∂p which appears in the expansion of the
individual time derivative. This fact permits a shortcut in the derivation. We simply
take the divergence of this term,
∇
h
·
ω
∂v
h
∂p
= ω
∂D
∂p
+∇
h
ω ·
∂v
h
∂p
with D =∇
h
· v
h
(23.12)
23.5 The first and second filter conditions 595
Fig. 23.1 Interpr
etation of the twisting term.
and then add the result to equation (15.63). This gives the baroclinic divergence
equation
∂D
∂t
+ v
h
·∇
h
D + D
2
+ ω
∂D
∂p
+∇
h
ω ·
∂v
h
∂p
+ 2J (v, u)
− k ·
∇
h
× (f v
h
)
=−∇
2
h
φ
(23.13)
which will be used later. Once again, we consider equations (23.10) and (23.13) to
be equivalent to the horizontal equation of motion.
23.5 The first and second filter conditions
As in Section 22.4 we introduce an artificial boundary condition by replacing the
lower boundary by a rigid surface p = p
0
= 1000 hPa. This results in the first filter
condition (22.31), which is not repeated here. Since we are studying the flow on the
tangential plane, i.e. m
0
= 1, we conclude that the covariant velocities v
1
and v
2
are
identical with the physical velocity components u and v. As discussed previously,

596 A quasi-geostrophic baroclinic model
the lower rigid boundary eliminates external gravity waves, which would form if
the lower boundary were free to oscillate. The first filter condition states that, at the
initial time t
0
= 0, the horizontal velocity components (u, v) cannot be prescribed
without any restriction, but rather must obey the condition (22.31). We will now
introduce the second filter condition to eliminate horizontal sound waves, internal
gravity waves, and possibly inertial waves characterized by the frequency f/k.We
proceed as follows.
With the help of the continuity equation of the p system (22.23) we replace the
horizontal divergence ∇
h
·v
h
in term III of the unfiltered vorticity equation (23.10)
by −∂ω/∂p. In the remaining terms the wind is assumed to be nondivergent so that
v
h
may be expressed by a stream function:
v
h
= k ×∇
h
ψ, u =−
∂ψ
∂y
,v=
∂ψ
∂x
(23.14)
Since the divergence term is exempted from the filtering process we speak of
selective filtering. On specifying the stream function as
ψ = φ/f
0
(23.15)
we see that the horizontal wind is very similar to the geostrophic wind. The only
difference is that the Coriolis parameter f occurring in the definition of v
g
has been
replaced by the constant f
0
representing an area average of the Coriolis parameter.
We have shown in (6.12) that the horizontal wind may be decomposed as
v
h
= k ×∇
h
ψ +∇
h
χ (23.16)
These two components represent the rotational part and the divergence part of the
wind field. We might proceed by introducing equation (23.16) into the heat equation
and the vorticity equation and then set ψ = φ/f
0
. This unselective filtering results
in a less drastic simplification of the physics but in more complicated equations.
For simplicity we will restrict ourselves to a model based on selective filtering.
In order to preserve important integral properties (averages expressed by inte-
grals) of the filtered system, it is necessary to introduce additional modifications
and simplifications into the predictive equations. We will now discuss in detail the
filtering of the heat equation and the vorticity equation. The introduction of the
stream function (23.15) into (23.14) results in a nondivergent wind, which we will
call the geostrophic wind. The vorticity resulting from the geostrophic wind will
be called the geostrophic vorticity:
v
g
=
1
f
0
k ×∇
h
φ, ∇
h
· v
g
= 0,ζ
g
= k ·∇
h
× v
g
=
1
f
0
∇
2
h
φ (23.17)
23.6 The geostrophic approximation of the heat equation 597
Moreover, we require that the advection is replaced by the geostrophic advection.
If B represents a general field function then the geostrophic advection is given by
v
g
·∇
h
B =−
1
f
0
∂φ
∂y
∂B
∂x
+
1
f
0
∂φ
∂x
∂B
∂y
=
1
f
0
J (φ,B) = J (ψ, B)(23.18)
where the Jacobian has been introduced for brevity.
23.6 The geostrophic approximation of the heat equation
For simplicity we assume that we have adiabatic conditions so that the right-hand
side of (23.9) vanishes. Geostrophic filtering requires the replacement of the actual
horizontal wind by the geostrophic wind. Thus, the filtered heat equation is given
by
∂
∂t
∂φ
∂p
+
1
f
0
J
φ,
∂φ
∂p
=−
σ
0
ω (23.19)
In this equation we have replaced the static stability σ
0
(x,y, p, t) by its horizontal
average σ
0
(p, t). This has been done in order to preserve some integral properties of
the predictive system. Integral properties of the system are characteristic features
that are obtained if we average the model equations over a certain atmospheric
region.
A detailed but qualitative justification for the introduction of
σ
0
into (23.19)
will now be given. To facilitate the discussion we employ the unfiltered heat
equation in the temperature form (23.5), assuming that we have adiabatic conditions
for consistency. Thus, we obtain
∂T
∂t
+∇
h
· (v
h
T ) = T ∇
h
· v
h
+
p
R
0
σ
0
ω (23.20a)
The filtered heat equation is found by introducing the divergence-free geostrophic
wind (23.17) into the previous equation:
∂T
∂t
+∇
h
· (v
g
T ) =
p
R
0
σ
0
ω (23.20b)
By means of the integral operator
B =
1
A
A
Bdxdy (23.21)
we introduce the average of the arbitrary field function B over the horizontal area
A which is a part of a pressure surface. The very small inclination of A relative
598 A quasi-geostrophic baroclinic model
to the (x,y)-plane has been ignored. Thus, the average horizontal divergence is
defined by
∇
h
· v
h
=
1
A
A
∇
h
· v
h
dxdy =
1
A
A
v
h
· ds,ds = dr × k (23.22a)
where we have used the two-dimensional divergence theorem (M6.34). Here ds is a
vector line element perpendicular to
A
. Assuming that we have vanishing normal
components of the horizontal and the geostrophic wind vector along the boundary
of A, the average divergence is zero. If ds is normalized then v
h
· ds is the normal
component of v
h
on
A
. As an example, we choose A as a rectangle with sides
parallel to the coordinate axis. Then we obt
ain
∇
h
· v
h
=
1
A
A
(udy − vdx) = 0, ∇
h
· Bv
h
= 0, ∇
h
· Bv
g
= 0
(23.22b)
This type of situation occurs if A comprises a region with a periodic continuation
of the wind field. Had we taken the average over a pressure surface enclosing the
earth, we would have obtained the same result since a spherical surface has no
boundary.
We will now apply the averaging formula (23.21) to the unfiltered and filtered
forms of the heat equation, (23.20a) and (23.20b). Since the divergence terms
vanish, we find for the unfiltered system
∂
T
∂t
=
TD+
p
R
0
σ
0
ω (23.23a)
and for the filtered system
∂
T
∂t
=
p
R
0
σ
0
ω (23.23b)
The two systems differ by the term
TD = T ∇
h
· v
h
. As the next step we will
qualitatively estimate the effect produced by the term TD by considering the cor-
relations between T and D =∇
h
· v
h
for a development situation characterized by
intensifying cyclones and anticyclones.
We proceed by dividing the atmosphere into an upper and a lower section. The
separating pressure surface p
lnd
is placed at the level of nondivergence, which is
usually located between the 500- and 600-hPa pressure surfaces. Hence, we have
D(p
lnd
) = 0. Above or below p
lnd
we assume that the sign of D is uniform in each
subregion. In the real atmosphere more than one pressure level p
lnd
may occur.
Figure 23.2 depicts the qualitative behaviors of the variables (D, T, ω, σ
0
)in
the subregions of rising and sinking air within the developing region A.Atany
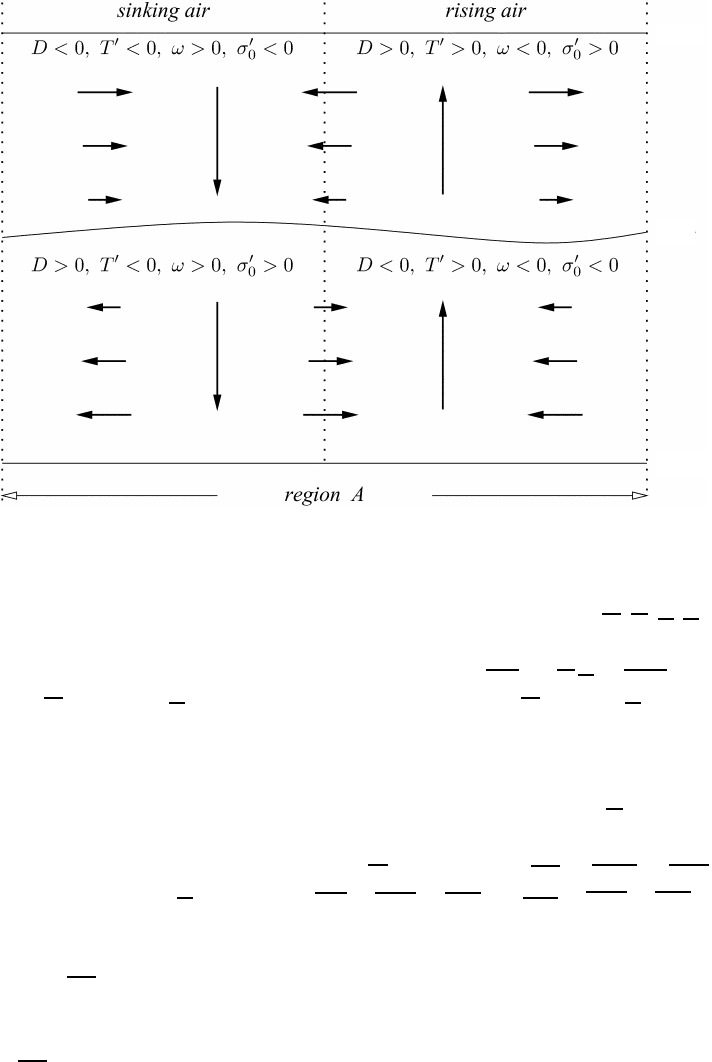
23.6 The geostrophic approximation of the heat equation 599
p = 0
p
lnd
p = p
0
g
Fig. 23.2 Behaviors of variables in the subregions
of rising and sinking air within the
developing region A.
height the horizontal average values of the variables within A are (D, T,ω, σ
0
)
while the deviations from the average values are denoted by (D
,T
,ω
,σ
0
). For
any pair of these variables the correlation product is
ψχ = ψ χ + ψ
χ
with
ψ = ψ + ψ
,χ = χ + χ
,andψ, χ = T,D,ω,σ
0
.SinceD = 0andω = 0we
have D
= D and ω
= ω. The signs of D and ω in the subregions of rising and
sinking air follow immediately from the assumed directions of flow indicated in
the figure. In the subregion of sinking air motion we expect colder temperatures
than the average temperature of the entire region A so that there T<
T or T
< 0.
In the subregion of rising air the opposite situation is observed, that is T
> 0. Note
that T
is a temperature difference. Since D = 0 we obtain TD = T
D
= T
D.
Analogously, due to ω = 0wehaveTω = T
ω
= T
ω and σ
0
ω = σ
0
ω
= σ
0
ω.
Let us consider the upper section of the atmosphere. In the upper subregion of
sinking air we see that D<0andT
< 0 so that in this subregion the correlation
product TD is positive. In the upper subregion of rising air we have D>0andT
>0
so that there the correlation is also greater than zero. This means that, throughout
the upper section of the atmosphere, the correlation of temperature and divergence
is
TD > 0. We proceed similarly with the lower section and with the remaining
variables.

600 A quasi-geostrophic baroclinic model
p = 0
p = p
0
Fig. 23.3 Changes of the atmospheric stability σ
0
in the subregions of rising and sinking
air within the developing region A. Full curves: initial temperature profiles; dashed curves:
modified temperature profiles after vertical motion.
To study the correlation between the static stability σ
0
and the vertical velocity
ω in the subregions of rising and sinking air, we refer to Figure 23.3. Assuming
that T<T in the left section of the developing region and T>T in the right
section we obtain sinking and rising air motion as discussed for Figure 23.2.
At the upper and lower boundaries of the atmosphere ω vanishes, so the temperature
remains constant there. Obviously, sinking air motion results in dry adiabatic
heating whereas rising air motion causes dry adiabatic cooling. The maximum
change in temperature is expected at the level of nondivergence where the vertical
velocity is largest. According to (23.3) σ
0
∝ − γ , so the relation between σ
0
and σ
0
shown in Figure 23.3 is easily verified. This yields the σ
0
distribution
shown in Figure 23.2 and therefore the correlations σ
0
ω<0 in the upper section
and σ
0
ω>0 in the lower section of the atmosphere. In summary we expect the
following correlations:
p<p
lnd
: TD >0, σ
0
ω<0, Tω <0
p>p
lnd
: TD <0, σ
0
ω>0, Tω <0
(23.24)
Before continuing our discussion of the correlations it will be helpful to make the
following observations.
