Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

20.8 The equation of motion in Lagrangian enumeration coordinates 561
According to (18.64) the Lagrangian function L = K
A
− φ
a
for the Cartesian
coordinates of the stereographic projection is given by
L =
1
2m
2
[( ˙x
1
)
2
+ ( ˙x
2
)
2
+ 2( ˙x
2
x
1
− x
2
˙x
1
)] +
( ˙x
3
)
2
2
+
2
2m
2
(x
1
)
2
+ (x
2
)
2
− φ
a
(20.77)
We now make use of the metric simplification m = 1, which requires that must
be replaced by sin ϕ = f/2 since we leave the stereographic plane and go to the
tangential plane. Therefore, the metrically simplified form reads
L =
1
2
[( ˙x
1
)
2
+ ( ˙x
2
)
2
+ ( ˙x
3
)
2
+ f ( ˙x
2
x
1
− x
2
˙x
1
)] − φ (20.78)
In the basic system of Cartesian coordinates of the stereographic projection the
Coriolis force may be written as
−2Ω
+
× v =−f a
3
× (a
1
˙x
1
+ a
2
˙x
2
+ a
3
˙x
3
)
=
f
m
2
a
1
˙x
2
− a
2
˙x
1
= C
x
1
a
1
+ C
x
2
a
2
+ C
x
3
a
3
= C
x
n
a
n
(20.79)
The +above Ω was placed there to show that, in general, the direction of the rotation
differs from the rotational direction in the geographical coordinates. Whereas Ω
+
has a fixed direction and cannot be decomposed, the rotational vector Ω can be split
in two components. On setting m = 1 we find for the covariant measure numbers
C
x
1
= f ˙x
2
,C
x
2
=−f ˙x
1
,C
x
3
= 0(20.80)
Finally, according to (20.68), the transformation of these measure numbers to the
Lagrangian enumeration coordinates yields
C
a
k
= C
x
n
∂x
n
∂a
k
(20.81)
Owing to the special properties ( ˙a
i
= 0) of the Lagrangian enumeration coor-
dinates we must write the Lagrangian equation of motion in the form
lim
˙a
k
→0
d
dt
∂L
∂ ˙a
k
−
∂L
∂a
k
˙a
k
=−
1
ρ
∂p
∂a
k
(20.82)
562 The stereographic coordinate system
The substitution of (20.78) into (20.82) is somewhat complex, therefore we shall
proceed stepwise. Recalling (3.58) and (20.76), we may first write
lim
˙a
k
→0
∂L
∂ ˙a
k
= lim
˙a
k
→0
˙x
1
∂ ˙x
1
∂ ˙a
k
+ ˙x
2
∂ ˙x
2
∂ ˙a
k
+ ˙x
3
∂ ˙x
3
∂ ˙a
k
+
f
2
x
1
∂ ˙x
2
∂ ˙a
k
− x
2
∂ ˙x
1
∂ ˙a
k
= ˙x
1
∂x
1
∂a
k
+ ˙x
2
∂x
2
∂a
k
+ ˙x
3
∂x
3
∂a
k
+
f
2
x
1
∂x
2
∂a
k
− x
2
∂x
1
∂a
k
=
∂x
1
∂t
a
k
∂x
1
∂a
k
+
∂x
2
∂t
a
k
∂x
2
∂a
k
+
∂x
3
∂t
a
k
∂x
3
∂a
k
+
f
2
x
1
∂x
2
∂a
k
− x
2
∂x
1
∂a
k
= A
(20.83)
Observing (3.58) once again, we obtain
lim
˙a
k
→0
d
dt
∂L
∂ ˙a
k
=
∂A
∂t
a
k
=
∂
2
x
1
∂t
2
a
k
∂x
1
∂a
k
+
∂
2
x
2
∂t
2
a
k
∂x
2
∂a
k
+
∂
2
x
3
∂t
2
a
k
∂x
3
∂a
k
+
∂x
1
∂t
a
k
∂
2
x
1
∂t ∂a
k
+
∂x
2
∂t
a
k
∂
2
x
2
∂t ∂a
k
+
∂x
3
∂t
a
k
∂
2
x
3
∂t ∂a
k
+
f
2
∂x
1
∂t
a
k
∂x
2
∂a
k
+ x
1
∂
2
x
2
∂t ∂a
k
−
∂x
2
∂t
a
k
∂x
1
∂a
k
− x
2
∂
2
x
1
∂t ∂a
k
(20.84)
For the second term on the left-hand side of (20.82) we find from (20.78) the
following expression:
lim
˙a
k
→0
−
∂L
∂a
k
˙a
k
=−˙x
1
∂ ˙x
1
∂a
k
− ˙x
2
∂ ˙x
2
∂a
k
− ˙x
3
∂ ˙x
3
∂a
k
−
f
2
x
1
∂ ˙x
2
∂a
k
+ ˙x
2
∂x
1
∂a
k
− x
2
∂ ˙x
1
∂a
k
− ˙x
1
∂x
2
∂a
k
+
∂φ
∂a
k
=−
∂x
1
∂t
a
k
∂
2
x
1
∂t ∂a
k
−
∂x
2
∂t
a
k
∂
2
x
2
∂t ∂a
k
−
∂x
3
∂t
a
k
∂
2
x
3
∂t ∂a
k
−
f
2
x
1
∂
2
x
2
∂t ∂a
k
+
∂x
2
∂t
a
k
∂x
1
∂a
k
− x
2
∂
2
x
1
∂t ∂a
k
−
∂x
1
∂t
a
k
∂x
2
∂a
k
+
∂φ
∂a
k
(20.85)
Substitution of (20.84) and (20.85) into (20.82) results in a number of terms
canceling out. The equation of motion in terms of the Lagrangian enumeration

20.8 The equation of motion in Lagrangian enumeration coordinates 563
coordinates now reads
∂
2
x
1
∂t
2
a
k
∂x
1
∂a
k
+
∂
2
x
2
∂t
2
a
k
∂x
2
∂a
k
+
∂
2
x
3
∂t
2
a
k
∂x
3
∂a
k
=−
1
ρ
∂p
∂a
k
−
∂φ
∂a
k
+ f
∂x
2
∂t
a
k
∂x
1
∂a
k
−
∂x
1
∂t
a
k
∂x
2
∂a
k
with
∂x
1
∂t
a
k
= ˙x
1
,
∂x
2
∂t
a
k
= ˙x
2
(20.86)
The last term on the right-hand side of this equation represents the Coriolis effect.
With the help of (20.80) and (20.81) the Coriolis part of the equation of motion
can then be written as
f
˙x
2
∂x
1
∂a
k
− ˙x
1
∂x
2
∂a
k
= C
x
1
∂x
1
∂a
k
+ C
x
2
∂x
2
∂a
k
= C
a
k
(20.87)
so that (20.86) assumes the form
∂
2
x
n
∂t
2
a
k
∂x
n
∂a
k
=−
1
ρ
∂p
∂a
k
−
∂φ
∂a
k
+ C
a
k
(20.88)
This equation can often be found in the literature, but usually without the Coriolis
effect. Together with the continuity equation we now have a system of four scalar
equations from which to determine the variables u, v, w,andρ.
It is possible to write (20.88) in still another form by applying a Legendre
transformation and by using (3.58) again. For the left-hand side of (20.88) we find
∂
2
x
n
∂t
2
a
k
∂x
n
∂a
k
=
∂
∂t
a
k
∂x
n
∂t
∂x
n
∂a
k
−
∂
∂a
k
∂x
n
∂t
a
k
∂x
n
∂t
a
k
=
∂
∂t
a
k
˙x
n
∂x
n
∂a
k
−
1
2
∂
∂a
k
∂x
n
∂t
a
k
∂x
n
∂t
a
k
=
∂
∂t
a
k
˙x
n
∂x
n
∂a
k
−
∂
∂a
k
v
2
2
with v
2
= g
x
nn
˙x
n
˙x
n
= ˙x
n
˙x
n
(m = 1org
x
ii
= 1)
(20.89)
Substituting (20.89) into (20.88) results in the following version of the equation
of motion in terms of the Lagrangian enumeration coordinates:
∂
∂t
a
k
˙x
n
∂x
n
∂a
k
=−
1
ρ
∂p
∂a
k
+
∂
∂a
k
v
2
2
− φ
+ C
a
k
(20.90)

564 The stereographic coordinate system
By using the transformation equation (20.81), we find in place of (20.90) the very
convenient form
∂
∂t
a
k
v
a
k
=−
1
ρ
∂p
∂a
k
+
∂
∂a
k
v
2
2
− φ
+ C
a
k
(20.91)
Sometimes the pressure term is replaced by the thermodynamic relation
−
1
ρ
δp = T δs − δh (20.92)
where s and h denote the specific entropy and the specific enthalpy. With δ = ∂/∂a
k
equation (20.91) is given the final form
∂
∂t
a
k
v
a
k
=
∂
∂a
k
v
2
2
− φ − h
+ T
∂s
∂a
k
+ C
a
k
(20.93)
This equation, the continuity equation, the first law of thermodynamics, and the
ideal-gas law give a complete system from which to determine the nonturbulent
flow of unsaturated air.
20.9 Problems
20.1:
(a) Use Lagrange’s equation of motion to verify the second equation of (20.43).
(b) Transform the first equation of (20.43) to obtain the first equation of (20.46).
(c) Transform the first equation of (20.46) to obtain the first equation of (20.48).
20.2: Verify that equation (20.67) is a solution by substituting u(z, t)andv(z, t)
into the first equation of (20.66).
20.3: On the Mercator and Bond map the surface of the earth is represented by
a Cartesian system in such a way that latitude circles are parallel to the x-axis
and longitude circles are parallel to the y-axis. The representation is due to the
differential transformation relations dx = rdλand dy = rdϕ/cos ϕ.
(a) Show that the representation is conformal. Find the map factor m.
(b) Starting with the rigidly rotating geographical coordinate system, find the
following quantities: the metric fundamental form (dr)
2
, kinetic energy K
A
,metric
fundamental quantities g
ij
,g
ij
,
√
g, and covariant and physical measure numbers
of the relative velocity v.
(c) Replace z by the pressure coordinate p and find
√
g
p
. Assume the validity of the
hydrostatic equation.

21
Orography-following coordinate systems
21.1 The metric of the η system
Suppose that we wish to model the air flow over a limited region of the earth’s
surface so that the effect of the earth’s curvature on the flow may be ignored. In
this case we may set the map factor m
0
= 1 so that the air flow refers to the
tangential plane. The flow, however, might be strongly influenced by orographic
effects. The question which now arises quite naturally is that of how the effects of
the lower boundary on the flow should be formulated. It is always possible to state
the lower boundary condition in the presence of orography by using the orthogonal
Cartesian system but the formulation might be quite unwieldy. A far superior
method for handling orography is to replace the Cartesian vertical coordinate z by
a new vertical coordinate η, which is formulated in such a way that the surface
of the earth coincides with a surface of the new vertical coordinate. We call this
coordinate system the η system. The relation between the coordinate z and the new
coordinate η is defined by the following transformation:
η =
z − H
H − h(x, y)
= η (x, y,z) =⇒ z(x, y,η) = η[H − h(x,y)] + H (21.1)
In this formula H represents a fixed upper boundary of the model region while
h(x,y) describes the orography. The new coordinate system is not orthogonal, so the
equation of motion assumes a form that is more complicated than before. We admit
only rigid rotation so that the coordinate surfaces of the η system do not deform.
By introducing the η-coordinate the mathematical complexity is overcompensated
by the effectiveness in the numerical evaluation of the flow model.
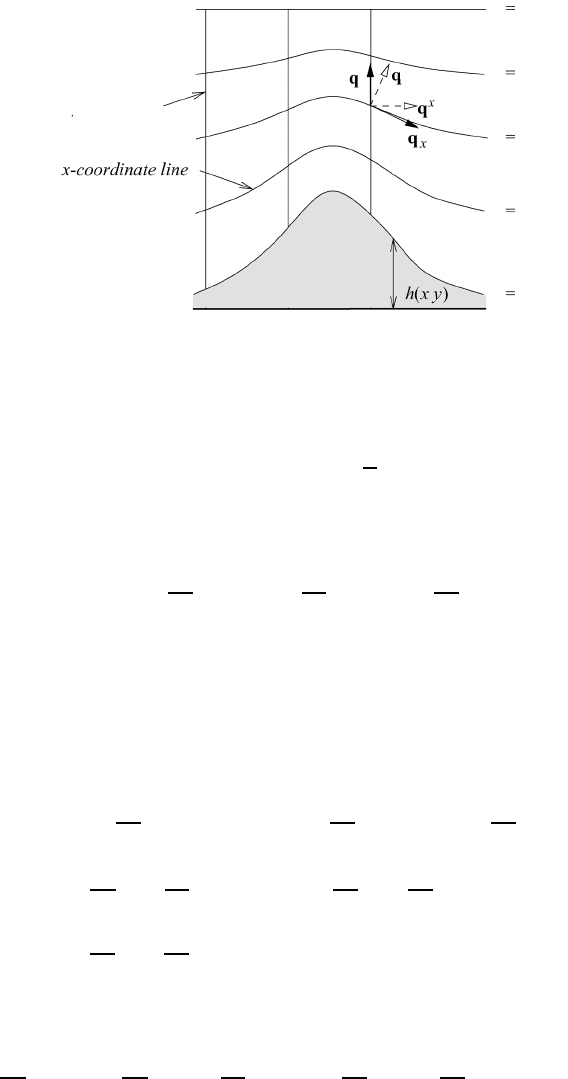
In order to visualize the transformation procedure we consider the idealized sit-
uation depicted in Figure 21.1. The covariant basis vectors q
x
and q
η
are tangential
to the x-andη-coordinate lines while the contravariant basis vectors q
x
and q
η
point in the direction of the gradients ∇q
i
, see (M3.27), since q
i
=∇q
i
. We would
565
566 Orography-following coordinate systems
0.0
−0.5
−0.75
−1.0
−0.25
η
η
η
-coordinate line
η
η
η
η
η
,
Fig. 21.1 A schematic
representation of orography.
like to point out that we are dealing with a right-handed coordinate system. Had
we taken the numerator of (21.1) as H − z then the surface of the earth would
be defined by η = 1, describing a left-handed coordinate system. As will be seen
soon, in this case the functional determinant
√
g assumes negative values.
The elements of the metric tensor or the metric fundamental quantities g
ij
can
be found by substituting
dz =
∂z
∂x
y,η
dx +
∂z
∂y
x,η
dy +
∂z
∂η
x,y
dη (21.2)
into the metric fundamental form of the Cartesian system,
(dr)
2
= (dx)
2
+ (dy)
2
+ (dz)
2
(21.3)
This yields
(dr)
2
=
1 +
∂z
∂x
2
y,η
(dx)
2
+
1 +
∂z
∂y
2
x,η
(dy)
2
+
∂z
∂η
2
x,y
(dη)
2
+ 2
∂z
∂x
y,η
∂z
∂y
x,η
dx dy + 2
∂z
∂x
y,η
∂z
∂η
x,y
dx dη
+ 2
∂z
∂y
x,η
∂z
∂η
x,y
dy d η
(21.4)
The required partial derivatives are obtained from the transformation (21.1) as
∂z
∂x
y,η
=−η
∂h
∂x
,
∂z
∂y
x,η
=−η
∂h
∂y
,
∂z
∂η
x,y
= H − h (21.5)
21.1 The metric of the η system 567
Comparison of (21.4) with the general relation (dr)
2
= g
nm
dq
n
dq
m
gives all
components of the metric tensor:
g
11
= 1 +η
2
∂h
∂x
2
,g
12
= η
2
∂h
∂x
∂h
∂y
,g
13
=−η
∂h
∂x
(H − h)
g
21
= g
12
,g
22
= 1 +η
2
∂h
∂y
2
,g
23
=−η
∂h
∂y
(H − h)
g
31
= g
13
,g
32
= g
23
,g
33
= (H − h)
2
(21.6)
In the work to follow we will also need the contravariant components g
ij
.A
convenient way to find the g
ij
is to evaluate the transformation rule (M4.19):
g
ij
q
=
∂q
i
∂a
m
∂q
j
∂a
n
g
mn
a
,q
i
= (x,y,η),a
i
= (x,y, z),g
ij
a
= δ
ij
(21.7)
An example of (21.7) is given next in order to find the components g
23
η
of the metric
tensor:
g
23
η
=
∂y
∂x
y,z
∂η
∂x
y,z
+
∂y
∂y
x,z
∂η
∂y
x,z
+
∂y
∂z
x,y
∂η
∂z
x,y
=
η
H − h
∂h
∂y
∂η
∂x
y,z
=
η
H − h
∂h
∂x
,
∂η
∂y
x,z
=
η
H − h
∂h
∂y
,
∂η
∂z
x,y
=
1
H − h
(21.8)
The complete contravariant metric tensor g
ij
is listed below:
g
11
= 1,g
12
= 0,g
13
=
η
H − h
∂h
∂x
g
21
= g
12
,g
22
= 1,g
23
=
η
H − h
∂h
∂y
g
31
= g
13
,g
32
= g
23
,g
33
=
1
(H − h)
2
1 + η
2
∂h
∂x
2
+ η
2
∂h
∂y
2
(21.9)
In order to obtain the continuity equation of the η system we need to find the
functional determinant. This quantity is obtained from the general transformation
rule (M4.21):
√
g
q
=
√
g
a
∂(a
1
,a
2
,a
3
)
∂(q
1
,q
2
,q
3
)
=⇒
√
g
η
=
√
g
z
∂z
∂η
x,y
= H − h,
√
g
z
= 1
(21.10)
This expression confirms our previous statement that the functional determinant
becomes negative if we choose H −z instead of z−H in the transformation relation
(21.1) for going between η and z.

568 Orography-following coordinate systems
21.2 The equation of motion in the η system
In order to proceed efficiently, we will first obtain various parts of the equation of
motion. Then it will be easy to write down the final covariant and contravariant
forms in the η system. The relations between the contravariant and covariant
velocity components are
˙q
1
= v
1
= ˙x, ˙q
2
= v
2
= ˙y, ˙q
3
= v
3
= ˙η, v
i
= g
in
v
n
(21.11)
and can be used whenever needed. Next we wish to obtain the gradient of the
geopotential
φ = gz = g[η(H − h) + H ](21.12)
yielding
∂φ
∂x
y,η
=−gη
∂h
∂x
,
∂φ
∂y
x,η
=−gη
∂h
∂y
,
∂φ
∂η
x,y
= g(H − h)(21.13)
Here the usual symbol g has been utilized for the gravitational acceleration since
confusion with the functional determinant
√
g is unlikely.
Next, we wish to obtain the components of the rotational dyadic by employing
equation (M5.48). The required components W
i
of the rotational velocity v
are
found with the help of (20.36). We are going to retain m
0
in the calculations and
set m
0
= 1 at the end of the analysis. Application of the general transformation
rule (M4.15) to the components of v
yields
W
q
i
=
∂a
n
∂q
i
q
k
W
a
n
(21.14)
with q
i
= x,y,η and a
i
= x,y,z. Both systems refer to the stereographic projec-
tion. From (20.36) we find
W
a
1
= W
1
=−
y
m
2
0
,W
a
2
= W
2
=
x
m
2
0
,W
a
3
= W
3
= 0(21.15)
Employing the transformation rule (21.14) yields
W
η
1
=−
y
m
2
0
,W
η
2
=
x
m
2
0
,W
η
3
= 0(21.16)

21.2 The equation of motion in the η system 569
For example, we find for the component ω
12
ω
12
=
1
2
∂
∂x
x
m
2
0
+
∂
∂y
y
m
2
0
=
m
2
0
1 +
m
2
0
2
x
∂
∂x
1
m
2
0
+ y
∂
∂y
1
m
2
0
=
m
2
0
sin ϕ =
f
2m
2
0
(21.17)
The last step follows with the help of (20.29) so that the Coriolis parameter f =
2 sin ϕ can be utilized.
The complete rotational tensor is given by
ω
11
= 0,ω
12
=
f
2m
2
0
,ω
13
= 0
ω
21
=−ω
12
,ω
22
= 0,ω
23
= 0
ω
31
= 0,ω
32
= 0,ω
33
= 0
(21.18)
which agrees with (20.42). For the evaluation of the contravariant form of the
equation of motion, given by (18.34), we need the relation
ω
k
i
= g
km
ω
im
(21.19)
Finally, we calculate the Christoffel symbols according to equation (21.9). The
evaluation is an easy but admittedly very tedious task. The result is
3
11
=−
η
H − h
∂
2
h
∂x
2
,
3
12
=−
η
H − h
∂
2
h
∂x ∂y
,
3
13
=−
1
H − h
∂h
∂x
3
21
=
3
12
,
3
22
=−
η
H − h
∂
2
h
∂y
2
,
3
23
=−
1
H − h
∂h
∂y
3
31
=
3
13
,
3
32
=
3
23
,
3
33
= 0
1
1i
= 0,
2
2i
= 0,i= 1, 2, 3
(21.20)
Now we have all the parts needed in order to evaluate the general covariant form
of the equations of motion (18.25) and general contravariant form (18.34). The
covariant equations of motion of the η system are given by
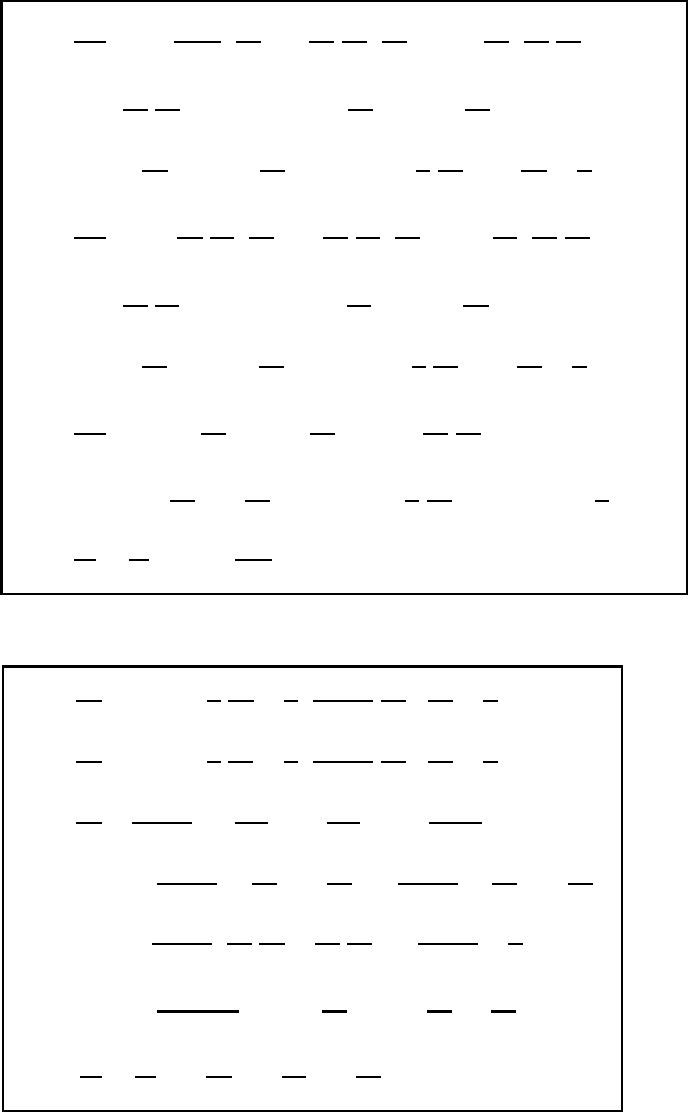
570 Orography-following coordinate systems
dv
1
dt
− η
2
˙x
2
2
∂
∂x
∂h
∂x
2
+
˙y
2
2
∂
∂x
∂h
∂y
2
+ ˙x ˙y
∂
∂x
∂h
∂x
∂h
∂y
−
˙η
2
2
∂
∂x
(H − h)
2
+ ˙ηη
˙x
∂
∂x
(H − h)
∂h
∂x
+ ˙y
∂
∂x
(H − h)
∂h
∂y
− f ˙y =−
1
ρ
∂p
∂x
+ gη
∂h
∂x
+
1
ρ
q
1
·∇ ·J
dv
2
dt
− η
2
˙x
2
2
∂
∂y
∂h
∂x
2
+
˙y
2
2
∂
∂y
∂h
∂y
2
+ ˙x ˙y
∂
∂y
∂h
∂x
∂h
∂y
−
˙η
2
2
∂
∂y
(H − h)
2
+ ˙ηη
˙x
∂
∂y
(H − h)
∂h
∂x
+ ˙y
∂
∂y
(H − h)
∂h
∂y
+ f ˙x =−
1
ρ
∂p
∂y
+ gη
∂h
∂y
+
1
ρ
q
2
·∇ ·J
dv
3
dt
− η
˙x
2
∂h
∂x
2
+ ˙y
2
∂h
∂y
2
+ 2 ˙x ˙y
∂h
∂x
∂h
∂y
+ ˙η
˙x
∂h
∂x
+ ˙y
∂h
∂y
(H − h) =−
1
ρ
∂p
∂η
− g(H − h) +
1
ρ
q
3
·∇ ·J
with
d
dt
=
∂
∂t
+ v
n
g
mn
∂
∂q
m
(21.21)
and those in the contravariant form are given by
d ˙x
dt
− f ˙y =−
1
ρ
∂p
∂x
−
1
ρ
η
H − h
∂h
∂x
∂p
∂η
+
1
ρ
q
1
·∇ ·J
d ˙y
dt
+ f ˙x =−
1
ρ
∂p
∂y
−
1
ρ
η
H − h
∂h
∂y
∂p
∂η
+
1
ρ
q
2
·∇ ·J
d ˙η
dt
−
η
H − h
˙x
2
∂
2
h
∂x
2
+ ˙y
2
∂
2
h
∂y
2
+ 2 ˙x ˙y
∂
2
h
∂x ∂y
−
2 ˙η
H − h
˙x
∂h
∂x
+ ˙y
∂h
∂y
+
fη
H − h
˙x
∂h
∂y
− ˙y
∂h
∂x
=−
η
H − h
∂h
∂x
∂p
∂x
+
∂h
∂y
∂p
∂y
−
g
H − h
+
1
ρ
q
3
·∇ ·J
−
1
(H − h)
2
1 + η
2
∂h
∂x
2
+ η
2
∂h
∂y
2
∂p
∂η
with
d
dt
=
∂
∂t
+ ˙x
∂
∂x
+ ˙y
∂
∂y
+ ˙η
∂
∂η
(21.22)
