Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


19.6 Problems 541
19.6 Problems
19.1: Use equation (18.52) and the information given in Section 19.1 to verify the
validity of the second equation of (19.11). Then use Lagrange’s equation of motion
to show that the second equation of (19.11) is correct. By a direct transformation
obtain the second equation of (19.12) from the second equation of (19.11).
19.2: Use the first metric simplification in conjunction with Lagrange’s equation
of motion to show that the underlined term in the first equation of (19.11) drops
out. Transform this equation to physical measure numbers of the velocity to show
that the two underlined terms in the first equation of (19.15) drop out.
19.3: Use the first metric simplification to show that the term 2w/r in equation
(19.31) vanishes.
19.4: The generalized coordinates of the elliptic coordinate system may be denoted
by q
i
= λ
,ϕ
,r
. The equations for transformation between the Cartesian and the
elliptic coordinates are then given by
x
1
= $ cosh r
cos ϕ
cos(λ
+ ), 0 ≤ λ
≤ 2π
x
2
= $ cosh r
cos ϕ
sin(λ
+ ), −π/2 ≤ ϕ
≤ π/2
x
3
= $ sinh r
sin ϕ
, 0 ≤ r
≤∞
where $ is the excentricity.
(a) Show that the kinetic energy of the elliptic coordinate system is given by
K
A
=
$
2
2
[(cosh
2
r
− cos
2
ϕ
)( ˙ϕ
2
+ ˙r
2
) + cosh
2
r
cos
2
ϕ
(
˙
λ
+ )
2
]
(b) Find g
11
from the definition (M4.8).
(c) Find the fundamental quantities g
ij
.
20
The stereographic coordinate system
For the analysis and depiction of meteorological data it is useful and customary to
map the surface of the earth onto a plane. Therefore, it is advisable for purposes of
numerical weather prediction to formulate and evaluate the atmospheric equations
in stereographic coordinates. Such a map projection should represent the spherical
surface as accurately as possible, but obviously some features will be lost. It is
extremely important to preserve the angle between intersecting curves such as the
right angle between latitude circles and meridians. Maps possessing this desirable
and valuable property are called conformal. If distances were preserved by mapping
the sphere onto the projection plane, the map would be called isometric. Mapping
from the sphere to the stereographic plane is conformal but not isometric. In order
to remove this deficiency to a tolerable level, a scale factor m, also called the image
scale, will be introduced.
20.1 The stereographic projection
We will now describe the sphere-to-plane mapping by introducing a projection
plane that is parallel to the equatorial plane. On the projection plane we may
construct a Cartesian (x,y,z)-coordinate system with a square rectangular grid.
The stereographic Cartesian coordinate system differs from the regular Cartesian
coordinates since the metric fundamental quantities are not g
ij
= δ
ij
.Infact,they
still contain the Gaussian curvature 1/r of the spherical coordinate system, showing
that in reality we have not left the sphere.
Conformal mapping means that the angle between two lines intersecting at a
certain point on the sphere is reproduced in magnitude and sense by the angle
between the corresponding curves on the plane. Infinitesimally small triangles
around such points on the sphere are mapped onto similar infinitesimally small
triangles on the plane. Moreover, a small circle remains a circle and an ellipse
542

20.1 The stereographic projection 543
( )
2
2
1
( )
(ds
r
)
1
(ds
r
)
Fig. 20.1 The infinitesimal surroundings of a point P
r
on the sphere and of the point P
E
on the projection plane.
transforms into an ellipse such that the ratio of the lengths of the major and minor
axes is preserved. This is demonstrated in Figure 20.1 for the infinitesimally small
area of elliptical shape. The point P
r
is somewhere on the sphere, and P
E
is located
on the projection plane symbolized by the subscript E. Since the ratio of a line
element on the sphere ds
r
to the line element mapped onto the projection plane
ds
E
is independent of the orientation of the line element we have
(ds
r
)
1
(ds
E
)
1
=
(ds
r
)
2
(ds
E
)
2
(20.1)
We will use this information to define the scale factor.
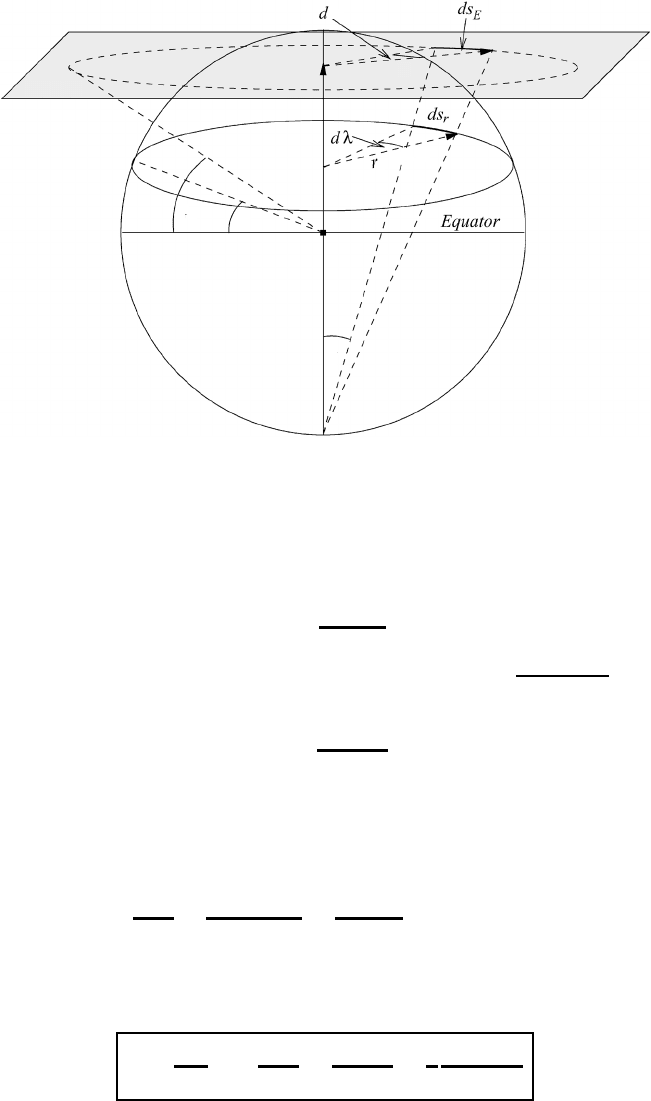
Let us consider the plane E
0
defined by the angle of latitude ϕ
0
shown in
Figure 20.2. The conformal stereographic map results from projecting an arbitrary
spherical reference surface within the atmosphere, defined by the radius r, onto the
plane E. This plane is parallel to E
0
and is located a distance r −r
0
above E
0
,where
r
0
is the mean radius of the earth. For a central projection the line element ds
r
,
defined by the latitudinal angle ϕ, now has a length ds
r
0
on the surface of the earth.
Obviously, the latitude and the longitude (ϕ,λ) do not change. The infinitesimal
line element ds
r
0
is first projected stereographically onto the plane E
0
, yielding
ds
E
0
, and then onto the plane E without any distortion, resulting in ds
E
.From
Figure 20.2 we see that the projection source is the south pole. Furthermore, we
have ds
r
0
=−r
0
dϕ and ds
E
0
= dR.
We will now define the scale or image factors for the earth’s surface m
0
= m(r
0
)
and the spherical reference surface m = m(r) by means of
m
0
=
ds
E
0
ds
r
0
=−
dR
r
0
dϕ
,m=
ds
E
ds
r
=−
dR
rdϕ
=⇒ m = m
0
r
0
r
(20.2)
As will be seen, the scale factors are independent of the longitude λ.
In order to establish the dependency of m on the latitude ϕ, we consider the
rectangular triangle formed by the sides l
0
+r
0
,R, and the projection ray extending
from the south pole at angle γ measured from the polar axis; see Figure 20.2. From
the figure we immediately find
(a) γ =
1
2
π
2
− ϕ
=
χ
2
,c= r
0
+ l
0
= r
0
(1 + sin ϕ
0
)
(b) tan γ =
R
r
0
+ l
0
=
R
c
=
sin χ
1 + cos χ
=
cos ϕ
1 + sin ϕ
(20.3)

544 The stereographic coordinate system
( )
0
0
0
0
0
0
−
ds
E
= dR
E(z = 0)
E(z)
ds
r
Fig. 20.2 Stereographic projection of a line element ds
r
on the longitudinal circle with
radius r onto the projection plane E(z) with height z = r − r
0
. The line element
on
E is
ds
E
.
where the angle χ is the co-latitude π/2 − ϕ. Equation (20.3b) makes use of a
well-known trigonometric identity. From (20.2) and (20.3b) upon differentiation
we obtain
m
0
(ϕ) =
c
r
0
1
1 + sin ϕ
(20.4)
showing that m
0
depends on the latitude only. By eliminating the constant c/r
0
we
find the desired form
m
0
=
1 + sin ϕ
0
1 + sin ϕ
(20.5)
where ϕ
0
is a fixed but arbitrary latitude. The Weather Services of Germany and
the USA use ϕ
0
= 60
◦
and ϕ
0
= 90
◦
, respectively.
20.1 The stereographic projection 545
cos
0
0
0
E(z = 0)
R
0
γ
Fig. 20.3 Stereographic projection of the line element ds
r
0
on the latitudinal circle with
radius r
0
cos ϕ onto the projection plane E(z = 0). The line element on E(z = 0) is ds
E
0
.
It will be useful to derive additional forms of the scale factor m. On replacing
the term 1/(1 + sin ϕ) in (20.4) by means of (20.3b) we find
m
0
=
R
r
0
cos ϕ
(20.6)
Substitution of (20.4) and (20.6) into the expression sin ϕ =
1 − cos
2
ϕ gives
m
0
=
c
2
+ R
2
2cr
0
(20.7)
Finally, we project stereographically a line element of a latitudinal circle onto
the plane E(z = 0) = E
0
as shown in Figure 20.3. Using the definition of m
0
given
in (20.6) we may write
m
0
=
ds
E
0
ds
r
0
=
Rdα
r
0
cos ϕdλ
=
R
r
0
cos ϕ
since dα = dλ (20.8)
Here we have used the cylindrical coordinates R and α. Summarizing, we may
write for the scale factor m
m =
ds
E
ds
r
=−
dR
rdϕ
=
R
r cos ϕ
=
c
r
1
1 + sin ϕ
(20.9)
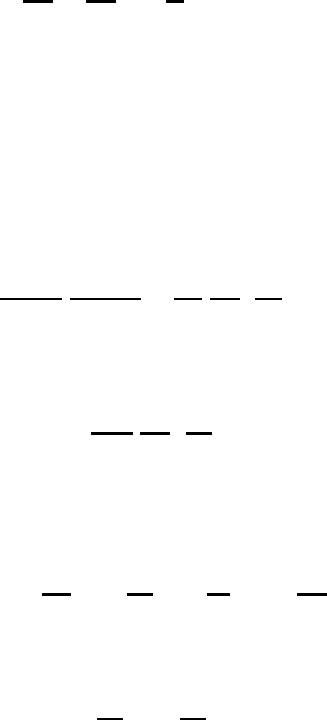
546 The stereographic coordinate system
Inspection of (20.9) shows that m depends not only on the latitude ϕ but also on
the radial distance r. The explicit dependence of m on r follows from (20.9):
∂m
∂r
=
∂m
∂z
=−
m
r
(20.10)
If we use the metric simplification r = r
0
= a then m = m
0
. Later we will make
use of this approximation since it will simplify our work without significant loss
of accuracy.
In order to introduce the Coriolis parameter f = 2 sin ϕ into the equation of
motion in stereographic coordinates, we need to derive an auxiliary relation. First
we write the trigonometric function sin ϕ with the help of equations (20.2) and
(20.6) in the form
sin ϕ =−
1
2cosϕ
d cos
2
ϕ
dϕ
=
m
2
0
2R
d
dR
R
2
m
2
0
(20.11)
from which it follows immediately that
sin ϕ = 1 +
m
2
0
R
2
d
dR
1
m
2
0
(20.12)
Thus, we have expressed the sine function in terms of the cylindrical coordinate R.
For the horizontal position vector in cylindrical coordinates R = q
R
R we may
write
R·∇ = q
R
R·
q
R
∂
∂R
+ q
α
∂
∂α
+ q
z
∂
∂z
= R
∂
∂R
(20.13)
Thus, we may express the sine function in (20.12) as
sin ϕ = 1 +
m
2
0
2
R·∇
1
m
2
0
(20.14)
where m
0
depends on R only, see (20.7), so that the total derivative in (20.12) may
be replaced by the partial derivative.
20.2 Metric forms in stereographic coordinates
Our first task is to derive an expression for the functional determinant in the stere-
ographic system by relating the various derivatives appearing in the geographical
system with coordinates (λ, ϕ, r) and the stereographic system with cylindrical
coordinates (R,α,z).

20.2 Metric forms in stereographic coordinates 547
Let us consider the unspecified function ψ which will be expressed in both
systems. Expressing ψ as a function of the longitude, i.e. ψ(λ) = ψ [α(λ)], we
obtain
∂ψ
∂λ
ϕ,r
=
∂ψ
∂α
R,z
dα
dλ
=
∂ψ
∂α
R,z
=⇒
1
r cos ϕ
∂ψ
∂λ
ϕ,r
=
m
R
∂ψ
∂α
R,z
(20.15)
where the geographical part r cos ϕ of (20.9) is appended to the geographical system
and m/R to the stereographic system. We proceed similarly with the remaining
partial derivatives. Since the longitude λ and the angle α correspond to each other,
as do r and z,wemaywrite
∂ψ
∂ϕ
λ,r
=
∂ψ
∂R
α,z
dR
dϕ
=⇒ −
1
r
∂ψ
∂ϕ
λ,r
= m
∂ψ
∂R
α,z
(20.16)
where again use of (20.9) has been made. Finally
∂ψ
∂r
λ,ϕ
=
∂ψ
∂z
R,α
(20.17)
is the obvious statement that dr = dz.
In order to find the functional determinant for the stereographic system we use
the well-known transformation formula (M4.21) which leads to
√
g
R,α,z
=
√
g
λϕ,r
∂(λ, ϕ, r)
∂(R, α,z)
= r
2
cos ϕ
010
−
cos ϕ
R
00
001
(20.18)
The various elements of the determinant can then be found by identifying in ψ
(20.15)–(20.17) with λ, ϕ,andr successively. For the case that ψ = λ this will
now be demonstrated:
m
∂λ
∂R
α,z
=−
1
r
∂λ
∂ϕ
λ,r
= 0
∂λ
∂α
R,z
=
R
mr cos ϕ
= 1
∂λ
∂z
R,α
=
∂λ
∂r
λ,ϕ
= 0
(20.19)

548 The stereographic coordinate system
Expanding the determinant and using (20.9), we get the desired result
√
g
R,α,z
= R/m
2
(20.20)
The next task is to find the metric fundamental quantities g
ij
for the stereographic
system in cylindrical coordinates. From (20.9) we find the basic relation for the
surfaces r = constant or z = constant
(ds)
2
spherical
=
1
m
2
(ds)
2
stereographic
(20.21)
In general we may write
(dr)
2
= (ds)
2
spherical
+ (dr)
2
=
1
m
2
(ds)
2
stereographic
+ (dz)
2
(20.22)
We apply this formula to the stereographic cylindrical coordinates and find
(dr)
2
= g
mn
dq
m
dq
n
=
1
m
2
(dR )
2
+ R
2
(dα)
2
+ (dz)
2
(20.23)
since the arclength element ds
stereographic
= dR e
R
+Rdαe
α
. Hence, we are dealing
with an orthogonal system. The covariant and contravariant metric fundamental
quantities g
ij
and g
ij
are easily found as
g
11
= 1/m
2
,g
22
= R
2
/m
2
,g
33
= 1,g
ij
= 0fori = j
g
11
= m
2
,g
22
= m
2
/R
2
,g
33
= 1,g
ij
= 0fori = j
(20.24)
since g
ii
g
ii
= 1. We proceed analogously with the Cartesian system. From (20.23)
we find with x = R cos α and y = R sin α
(dr)
2
= g
mn
dq
m
dq
n
=
1
m
2
(dx)
2
+ (dy)
2
+ (dz)
2
(20.25)
so that
g
11
= 1/m
2
,g
22
= 1/m
2
,g
33
= 1,g
ij
= 0fori = j
g
11
= m
2
,g
22
= m
2
,g
33
= 1,g
ij
= 0fori = j
(20.26)
Equation (20.14) can also be used to state the sine function in terms of the
Cartesian coordinates (x,y) by expressing the horizontal position vector R as
R = xq
x
+ yq
y
(20.27)
Therefore, we find
R·∇ = (xq
x
+ yq
y
)·
q
x
∂
∂x
+ q
y
∂
∂y
+ q
z
∂
∂z
= x
∂
∂x
+ y
∂
∂y
(20.28)
so that
sin ϕ = 1 +
m
2
0
2
x
∂
∂x
1
m
2
0
+ y
∂
∂y
1
m
2
0
(20.29)
20.3 The absolute kinetic energy in stereographic coordinates 549
20.3 The absolute kinetic energy in stereographic coordinates
There are several ways to derive an expression for the absolute kinetic energy in the
stereographic system. One possibility is to transform the absolute kinetic energy
of the geographical system,
K
A
=
1
2
r
2
cos
2
ϕ (
˙
λ + )
2
+ r
2
˙ϕ
2
+ ˙r
2
(20.30)
to the stereographic system. From equation (20.9) and the transformation relations
dλ = dα, dr = dz one obtains
˙
λ = ˙α, ˙ϕ =−
˙
R
mr
, ˙r = ˙z, cos ϕ =
R
mr
(20.31)
Substituting (20.31) into (20.30) results in the absolute kinetic energy of the stere-
ographic system in cylindrical coordinates:
K
A
=K + K
P
=
1
2
˙
R
2
+R
2
( ˙α
2
+2 ˙α)
m
2
+ ˙z
2
−φ
z
with K =
1
2
˙
R
2
+ R
2
˙α
2
m
2
+ ˙z
2
,K
P
=
R
2
˙α
m
2
− φ
z
,φ
z
=−
R
2
2
2m
2
(20.32)
where φ
z
represents the centrifugal potential.
Some useful relations between the Cartesian and the cylindrical coordinates are
summarized in
x = x
1
= R cos α, y = x
2
= R sin α, z = x
3
R =
x
2
+ y
2
,
˙
R =
x ˙x + y ˙y
x
2
+ y
2
d tan α
dt
=
˙α
cos
2
α
=
d
dt
y
x
, ˙α
2
=
˙x
2
+ ˙y
2
x
2
+ y
2
−
(x ˙x + y ˙y)
2
(x
2
+ y
2
)
2
(20.33)
Substituting these expressions into (20.32) gives the absolute kinetic energy of the
stereographic system in Cartesian coordinates:
K
A
= K + K
P
=
1
2
˙x
2
+ ˙y
2
+ 2( ˙yx − ˙xy)
m
2
+ ˙z
2
− φ
z
with K =
1
2
˙x
2
+ ˙y
2
m
2
+ ˙z
2
,K
P
=
( ˙yx − ˙xy)
m
2
− φ
z
,
φ
z
=−
(x
2
+ y
2
)
2
2m
2
(20.34)
The covariant measure numbers of the velocities v
P
are obtained by differentiat-
ing K
P
with respect to the contravariant measure numbers of the relative velocity.

550 The stereographic coordinate system
For the cylindrical coordinates from (20.32) we have
(W
1
,W
2
,W
3
) =
0,
R
2
m
2
, 0
, (W
1
,W
2
,W
3
) = (0,,0) (20.35)
In this expression the contravariant measure numbers are obtained by raising the
indices of the covariant measure numbers. From the relation g
ii
= ∂
2
K/(∂ ˙q
i
∂ ˙q
i
)
the validity of (20.24) may be easily checked.
For the kinetic energy in Cartesian coordinates as given by (20.34) the corre-
sponding result is
(W
1
,W
2
,W
3
) =
−
y
m
2
,
x
m
2
, 0
, (W
1
,W
2
,W
3
) = (−y, x , 0)
(20.36)
Again (20.26) may be obtained from g
ii
= ∂
2
K/(∂ ˙q
i
∂ ˙q
i
). Finally, in stereographic
cylindrical coordinates the measure numbers of the relative velocity are
(v
1
,v
2
,v
3
) = (
˙
R, ˙α, ˙z), (v
1
,v
2
,v
3
) =
˙
R
m
2
,
R
2
˙α
m
2
, ˙z
(20.37)
whereas in Cartesian coordinates they are given by
(v
1
,v
2
,v
3
) = ( ˙x, ˙y, ˙z), (v
1
,v
2
,v
3
) =
˙x
m
2
,
˙y
m
2
, ˙z
(20.38)
On utilizing these results in cylindrical coordinates the components of the absolute
velocity are given by
v
1
A
,v
2
A
,v
3
A
= (
˙
R, ˙α + , ˙z), (v
A,1
,v
A,2
,v
A,3
) =
˙
R
m
2
,
R
2
( ˙α + )
m
2
, ˙z
(20.39)
In the Cartesian coordinate system we obtain analogously
˙x
1
A
, ˙x
2
A
, ˙x
3
A
= ( ˙x − y, ˙y + x, ˙z)
( ˙x
A,1
, ˙x
A,2
, ˙x
A,3
) =
˙x − y
m
2
,
˙y + x
m
2
, ˙z
(20.40)
20.4 The equation of motion in the stereographic Cartesian coordinates
Before we evaluate the general equations in the covariant, the contravariant, and
the physical coordinate systems we need to state the components of the rotational
tensor and the Christoffel symbols of the second kind. In order to simplify the
pertinent equations we make use of the first metric simplification by setting r = a
