Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


20.4 The equation of motion in the stereographic Cartesian coordinates 551
so that m = m
0
. Substituting (20.26) into (19.9) yields for the Christoffel symbols
&
1
11
=−
1
2m
2
0
∂m
2
0
∂x
,&
1
12
=−
1
2m
2
0
∂m
2
0
∂y
,&
1
13
= 0
&
1
21
= &
1
12
,&
1
22
=
1
2m
2
0
∂m
2
0
∂x
,&
1
23
= 0
&
1
31
= 0,&
1
32
= 0,&
1
33
= 0
&
2
11
=
1
2m
2
0
∂m
2
0
∂y
,&
2
12
=−
1
2m
2
0
∂m
2
0
∂x
,&
2
13
= 0
&
2
21
= &
2
12
,&
2
22
=−
1
2m
2
0
∂m
2
0
∂y
,&
2
23
= 0
&
2
31
= 0,&
2
32
= 0,&
2
33
= 0
&
3
ij
= 0fori, j = 1, 2, 3
(20.41)
From equations (M5.48), (20.29), and (20.36) we find
ω
11
= 0,ω
12
=
f
2m
2
0
,ω
13
= 0
ω
21
=−ω
12
,ω
22
= 0,ω
23
= 0
ω
31
= 0,ω
32
= 0,ω
33
= 0
ω
k
i
= g
km
ω
im
,ω
*
ij
=
g
ii
g
jj
ω
ij
(20.42)
The computational labor leading to these equations is not excessive since we are
dealing with orthogonal coordinate systems.
Utilizing (20.26), (20.38), and (20.42) it is easy to evaluate the covariant equa-
tions of motion for rigid rotation (18.25):
dv
1
dt
+
v
2
1
+ v
2
2
2
∂m
2
0
∂x
− fv
2
=−
1
ρ
∂p
∂x
−
∂φ
∂x
+
1
ρ
q
1
·∇ ·J
dv
2
dt
+
v
2
1
+ v
2
2
2
∂m
2
0
∂y
+ fv
1
=−
1
ρ
∂p
∂y
−
∂φ
∂y
+
1
ρ
q
2
·∇ ·J
dv
3
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
q
3
·∇ ·J
with
d
dt
=
∂
∂t
+ m
2
0
v
1
∂
∂x
+ v
2
∂
∂y
+ v
3
∂
∂z
(20.43)
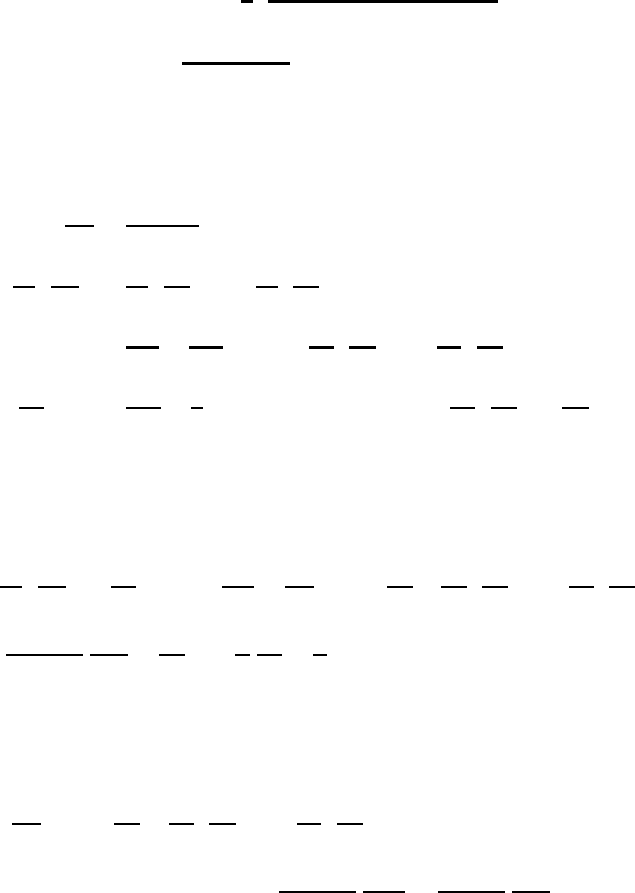
552 The stereographic coordinate system
To get some exercise with Lagrange’s formulation, we verify the first equation
of (20.43). From the Lagrangian function L,
L = K
A
− φ
a
=
1
2
˙x
2
+ ˙y
2
+ 2 (x ˙y − ˙xy)
m
2
0
+ ˙z
− φ
with φ = φ
a
−
(x
2
+ y
2
)
2
m
2
0
(20.44a)
we find with little effort
∂L
∂ ˙x
=
˙x − y
m
2
0
d
dt
∂L
∂ ˙x
=
d
dt
˙x
m
2
0
−
d
dt
y
m
2
0
=
dv
1
dt
−
˙y
m
2
0
− y
˙x
∂
∂x
1
m
2
0
+ ˙y
∂
∂y
1
m
2
0
∂
∂x
˙x
, ˙y
L =
˙y
m
2
0
+
1
2
[ ˙x
2
+ ˙y
2
+ 2(x ˙y − ˙xy)]
∂
∂x
1
m
2
0
−
∂φ
∂x
(20.44b)
Substitution of (20.44b) into the Lagrange equation of motion (18.65) yields
d
dt
∂L
∂ ˙x
−
∂
∂x
˙x
, ˙y
L =
dv
1
dt
−
2
m
2
0
˙y
1 +
m
2
0
2
x
∂
∂x
1
m
2
0
+ y
∂
∂y
1
m
2
0
˙x
2
+ ˙y
2
2m
4
0
∂m
2
0
∂x
+
∂φ
∂x
=−
1
ρ
∂p
∂x
+
1
ρ
q
1
·∇ ·J
(20.45a)
Utilizing (20.29) and (20.38), we have
2
m
2
0
˙y
1 +
m
2
0
2
x
∂
∂x
1
m
2
0
+ y
∂
∂y
1
m
2
0
= v
2
2 sin ϕ = fv
2
˙x
2
+ ˙y
2
2m
4
0
∂m
2
0
∂x
=
v
2
1
+ v
2
2
2
∂m
2
0
∂x
(20.45b)
Equation (20.45a) agrees with the first equation of (20.43).
20.4 The equation of motion in the stereographic Cartesian coordinates 553
The contravariant system is obtained by evaluating (18.34) with the help of
(20.41) and (20.42):
d ˙x
dt
+
˙y
2
− ˙x
2
2m
2
0
∂m
2
0
∂x
−
˙x ˙y
m
2
0
∂m
2
0
∂y
− f ˙y =−
m
2
0
ρ
∂p
∂x
− m
2
0
∂φ
∂x
+
1
ρ
q
1
·∇ ·J
d ˙y
dt
+
˙x
2
− ˙y
2
2m
2
0
∂m
2
0
∂y
−
˙x ˙y
m
2
0
∂m
2
0
∂x
+ f ˙x =−
m
2
0
ρ
∂p
∂y
− m
2
0
∂φ
∂y
+
1
ρ
q
2
·∇ ·J
d ˙z
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
q
3
·∇ ·J
with
d
dt
=
∂
∂t
+ ˙x
∂
∂x
+ ˙y
∂
∂y
+ ˙z
∂
∂z
(20.46)
The covariant system and the contravariant system are equivalent.
Whenever we are dealing with orthogonal coordinate systems, physical velocity
components offer some advantages. Owing to the rigidity of motion the basic
equation (18.37) is easy to evaluate. The required relations are summarized as
v
*
1
= u = ˙x/m
0
,v
*
2
= v = ˙y/m
0
,v
*
3
= w = ˙z
∂
∂q
*
1
= m
0
∂
∂x
,
∂
∂q
*
2
= m
0
∂
∂y
,
∂
∂q
*
3
=
∂
∂z
(20.47)
Hence, the equations of motion in stereographic Cartesian coordinates with physical
measure numbers are given by
du
dt
+ v
v
∂m
0
∂x
− u
∂m
0
∂y
− fv =−
m
0
ρ
∂p
∂x
− m
0
∂φ
∂x
+
1
ρ
e
1
·∇ ·J
dv
dt
− u
v
∂m
0
∂x
− u
∂m
0
∂y
+ fu =−
m
0
ρ
∂p
∂y
− m
0
∂φ
∂y
+
1
ρ
e
2
·∇ ·J
dw
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
e
3
·∇ ·J
with
d
dt
=
∂
∂t
+ m
0
u
∂
∂x
+ v
∂
∂y
+ w
∂
∂z
(20.48)
If the coordinate approximation is applied, i.e. φ = φ(z), then the partial derivatives
of φ with respect to x and y vanish in (20.43), (20.46), and (20.48).
We will now reexamine the geographical system. At the north pole this sys-
tem is undefined due to the appearance of tan ϕ in equations (2.26), (19.12), and

554 The stereographic coordinate system
(19.15). In contrast to this, the tan ϕ term does not appear in the stereographic
coordinate system. It should be observed that this term does not appear in the
covariant geographical system (19.11) either. This is certainly an advantage of the
covariant geographical system over the contravariant formulation.
Suppose that we wish to evaluate the system (19.15) numerically by using finite-
difference methods. The longitudinal term ∂/∂q
*
1
= (1/r cos ϕ) ∂/∂λ appearing
in the expansion of d/dt is latitude-dependent, so the numerical grid becomes
latitude-dependent also. This is an undesirable property. In contrast to this, the
Cartesian grid of the stereographic system is distorted only very slightly, which is
favorable for the numerical evaluation of the prognostic equations.
We now wish to establish the relation between the Cartesian coordinates of the
stereographic system and the coordinates of the geographical system. From (20.3),
(20.5), and (20.33) we have
x = R cos λ, y = R sin λ, R =
1 + sin ϕ
0
1 + sin ϕ
a cos ϕ = m
0
a cos ϕ
(20.49a)
In order to estimate the distances of the Cartesian grid in terms of the variables of
the geographical system, we expand dx and dy as
dx =
∂x
∂ϕ
λ
dϕ +
∂x
∂λ
ϕ
dλ, dy =
∂y
∂ϕ
λ
dϕ +
∂y
∂λ
ϕ
dλ (20.49b)
Evaluating the partial derivatives with the help of (20.49a) yields
dx
dy
= m
0
−sin λ −cos λ
cos λ −sin λ
dλ
*
dϕ
*
(20.49c)
with dλ
*
= a cos ϕdλand dϕ
*
= adϕ. It should be observed that the matrix stated
in (20.49c) is orthogonal, so the inversion of the system to find (dλ
*
,dϕ
*
) is easily
accomplished. For additional details see Haltiner and Williams (1980).
20.5 The equation of motion in stereographic cylindrical coordinates
As we have seen, it is possible to introduce not only Cartesian coordinates but
also cylindrical coordinates in the stereographic plane. We will proceed as in
Section 20.4. Again we use the approximation m = m
0
. The Christoffel symbols

20.5 The equation of motion in stereographic cylindrical coordinates 555
in cylindrical coordinates are given by
&
1
11
=
m
2
0
2
∂
∂R
1
m
2
0
,&
1
12
= 0,&
1
13
= 0
&
1
21
= 0,&
1
22
=−
m
2
0
2
∂
∂R
R
2
m
2
0
,&
1
23
= 0
&
1
31
= 0,&
1
32
= 0,&
1
33
= 0
&
2
11
= 0,&
2
12
=
m
2
0
2R
2
∂
∂R
R
2
m
2
0
,&
2
13
= 0
&
2
21
= &
2
12
,&
2
22
= 0,&
2
23
= 0
&
2
31
= 0,&
2
32
= 0,&
2
33
= 0
&
3
ij
= 0fori, j = 1, 2, 3
(20.50)
Comparison with (20.41) shows that more Christoffel symbols are zero than in the
Cartesian system. From (M5.48) and (19.7) we find
ω
11
= 0,ω
12
=
Rf
2m
2
0
,ω
13
= 0
ω
21
=−ω
12
,ω
22
= 0,ω
23
= 0
ω
31
= 0,ω
32
= 0,ω
33
= 0
ω
k
i
= g
km
ω
im
,ω
*
ij
=
g
ii
g
jj
ω
ij
(20.51)
The rotational dyadic exhibits the same simplicity as (20.42).
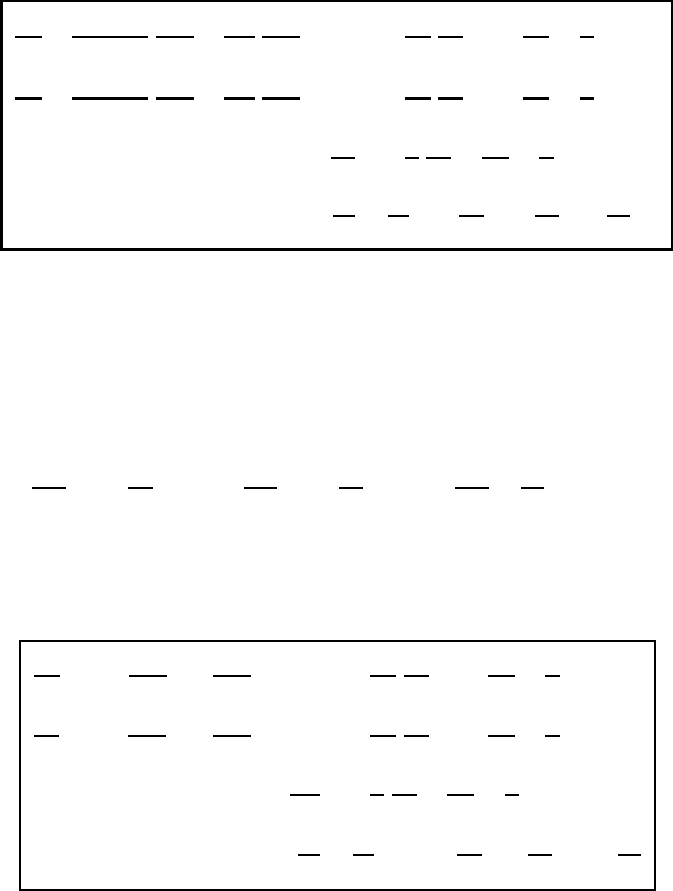
Substitution of (20.24), (20.38), and (20.51) into (18.25) results in the covariant
equations of motion
dv
1
dt
+
R
2
v
2
1
+ v
2
2
2R
2
∂m
2
0
∂R
−
v
2
2
m
2
0
R
3
−
fv
2
R
=−
1
ρ
∂p
∂R
−
∂φ
∂R
+
1
ρ
q
R
·∇ ·J
dv
2
dt
+ fv
1
R =−
1
ρ
∂p
∂α
−
∂φ
∂α
+
1
ρ
q
α
·∇ ·J
dv
3
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
q
z
·∇ ·J
with
d
dt
=
∂
∂t
+ m
2
0
v
1
∂
∂R
+
v
2
R
2
∂
∂α
+ v
3
∂
∂z
(20.52)
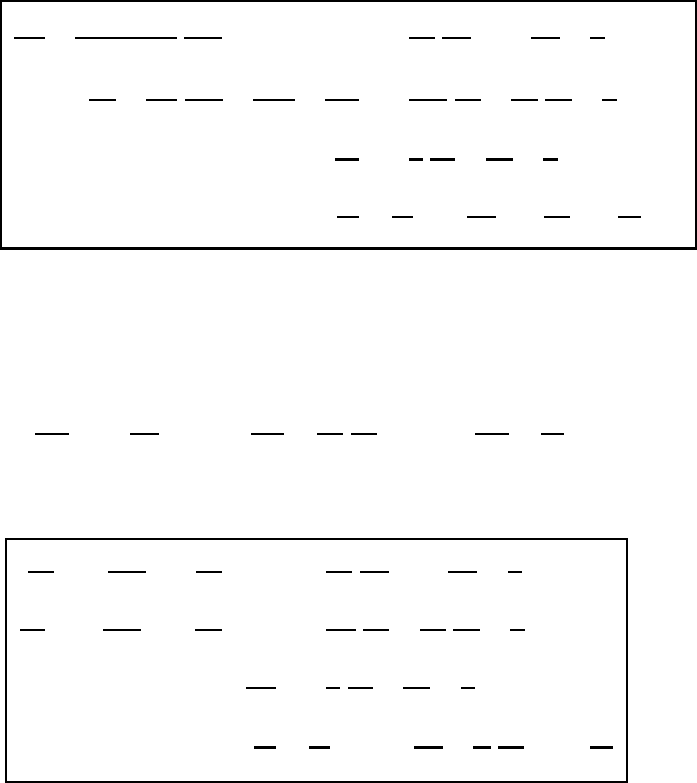
556 The stereographic coordinate system
On substituting (20.50) and (20.51) into (18.34), the contravariant counterparts are
analogously given as
d
˙
R
dt
−
˙
R
2
− ˙α
2
R
2
2m
2
0
∂m
2
0
∂R
− ˙α
2
R − f ˙αR =−
m
2
0
ρ
∂p
∂R
− m
2
0
∂φ
∂R
+
1
ρ
q
R
·∇ ·J
d ˙α
dt
−
˙α
˙
R
m
2
0
∂m
2
0
∂R
+
2 ˙α
˙
R
R
+
f
˙
R
R
=−
m
2
0
R
2
ρ
∂p
∂α
−
m
2
0
R
2
∂φ
∂α
+
1
ρ
q
α
·∇ ·J
d ˙z
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
q
z
·∇ ·J
with
d
dt
=
∂
∂t
+
˙
R
∂
∂R
+ ˙α
∂
∂α
+ ˙z
∂
∂z
(20.53)
In order to obtain the equations of motion in physical measure numbers we
evaluate (18.37). Utilizing (20.24), (20.51), and
v
*
1
= u =
˙
R/m
0
,v
*
2
= v = R ˙α/m
0
,v
*
3
= w = ˙z
∂
∂q
*
1
= m
0
∂
∂R
,
∂
∂q
*
2
=
m
0
R
∂
∂α
,
∂
∂q
*
3
=
∂
∂z
(20.54)
we find the desired equations of motion
du
dt
+ v
2
∂m
0
∂R
− v
2
m
0
R
− fv =−
m
0
ρ
∂p
∂R
− m
0
∂φ
∂R
+
1
ρ
e
1
·∇ ·J
dv
dt
− uv
∂m
0
∂R
+ uv
m
0
R
+ fu=−
m
0
Rρ
∂p
∂α
−
m
0
R
∂φ
∂α
+
1
ρ
e
2
·∇ ·J
dw
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
e
3
·∇ ·J
with
d
dt
=
∂
∂t
+ m
0
u
∂
∂R
+
v
R
∂
∂α
+ w
∂
∂z
(20.55)
The degree of complexity of this set of equations is about the same as that of
(20.48). If the coordinate approximation is applied, i.e. φ = φ(z), then the partial
derivatives of φ with respect to R and α vanish in (20.52), (20.53), and (20.55).
20.6 The continuity equation
In order to solve any prognostic system describing the atmospheric motion we also
need to solve the equation of continuity in addition to the heat equation and the

20.6 The continuity equation 557
ideal-gas law. In this section we will briefly derive the various versions of the
continuity equation. For the system describing rigid rotation the last term in (18.47)
vanishes. This equation can be easily rewritten in the form
dρ
dt
+
ρ
√
g
∂
∂q
n
(
√
g ˙q
n
) = 0(20.56)
For the various cases the continuity equation can now be obtained very easily.
Covariant stere
ographic Cartesian coordi
nates
1
ρ
dρ
dt
+ m
2
0
∂v
1
∂x
+
∂v
2
∂y
+
∂v
3
∂z
= 0(20.57)
Contravariant stereographic Cartesian coordinates
1
ρ
dρ
dt
+ m
2
0
∂
∂x
˙x
m
2
0
+
∂
∂y
˙y
m
2
0
+
∂ ˙z
∂z
= 0(20.58)
Physical stereographic Cartesian coordinates
1
ρ
dρ
dt
+ m
0
∂u
∂x
+
∂v
∂y
−
u
∂m
0
∂x
+ v
∂m
0
∂y
+
∂w
∂z
= 0(20.59)
Covariant stereographic cylindrical coordinates
1
ρ
dρ
dt
+
m
2
0
R
∂
∂R
(Rv
1
) +
∂
∂α
v
2
R
+
∂v
3
∂z
= 0(20.60)
Contravariant stereographic cylindrical coordinates
1
ρ
dρ
dt
+
m
2
0
R
∂
∂R
R
˙
R
m
2
0
+
∂
∂α
R ˙α
m
2
0
+
∂ ˙z
∂z
= 0(20.61)
Physical stereographic cylindrical coordinates
1
ρ
dρ
dt
+ m
0
∂u
∂R
+
1
R
∂v
∂α
+
∂w
∂z
+
m
0
u
R
− u
∂m
0
∂R
= 0(20.62)
In a later chapter we will integrate in principle various versions of the atmospheric
equations and then recognize more fully the importance of the continuity equation.
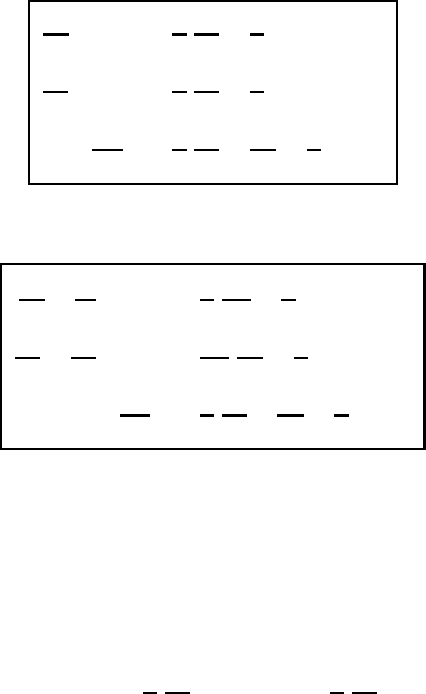
558 The stereographic coordinate system
20.7 The equation of motion on the tangential plane
In Section 2.5 we have introduced equations decribing the motion on the tangential
plane. This was done by fixing a rectangular coordinate system at the point of
observation on the surface of the earth. The z-axis is pointing to the local zenith
so that the x-andy- axes describe a tangential plane. The x-axis is pointing to the
east and the y-axis to the north, so the motion is described with respect to a right-
handed system. Going directly from the geographical coordinate system (19.15)
to the equation of motion on the tangential plane is not possible even if we delete
the underlined terms. Even on taking the radius of the earth as infinitely large to
approximate a plane, we still have a problem at the north pole. On the other hand,
if we set m
0
= 1, which corresponds to ϕ = ϕ
0
in (20.5), we obtain the equations
of motion with reference to the tangential plane directly. For the Cartesian system
we find from (20.48)
du
dt
− fv =−
1
ρ
∂p
∂x
+
1
ρ
e
1
·∇ ·J
dv
dt
+ fu =−
1
ρ
∂p
∂y
+
1
ρ
e
2
·∇ ·J
dw
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
e
3
·∇ ·J
(20.63)
The corresponding equations of the cylindrical system follow from (20.55) as
du
dt
−
v
2
R
− fv =−
1
ρ
∂p
∂R
+
1
ρ
e
1
·∇ ·J
dv
dt
+
uv
R
+ fu=−
1
Rρ
∂p
∂α
+
1
ρ
e
2
·∇ ·J
dw
dt
=−
1
ρ
∂p
∂z
−
∂φ
∂z
+
1
ρ
e
3
·∇ ·J
(20.64)
In (20.63) and (20.64) use of the coordinate approximation φ = φ(z) has been
made.
Geostrophic motion is a very simple but also a very useful approximation to
real flow, describing unaccelerated frictionless motion parallel to the isobars. By
neglecting in (20.63) frictional effects and setting the horizontal accelerations
du/dt = 0anddv/dt = 0 we obtain the well-known geostrophic wind relations
−fv
g
=−
1
ρ
∂p
∂x
,fu
g
=−
1
ρ
∂p
∂y
(20.65)

20.8 The equation of motion in Lagrangian enumeration coordinates 559
It is also possible to give an analytic solution to horizontal frictionless motion
on a horizontal plane if the advection term is ignored in the expansion of d/dt.In
this case (20.63) reduces to
∂u
∂t
− fv =−fv
g
,
∂v
∂t
+ fu = fu
g
(20.66)
By employing the somewhat complicated method of two-dimensional Laplace
transforms, see Voelker and Doetsch (1950), Chapter 5, we find the solution to the
coupled system
u(z, t) = u(z, 0) cos(ft) + v(z, 0) sin(ft)
− f
t
0
cos(ft
) v
g
(z, t − t
) dt
+ f
t
0
sin(ft
) u
g
(z, t − t
) dt
v(z, t) = v(z, 0) cos(ft) − u(z, 0) sin(ft)
+ f
t
0
cos(ft
) u
g
(z, t − t
) dt
+f
t
0
sin(ft
) v
g
(z, t − t
) dt
(20.67)
where the geostrophic wind components may be dependent on height and time.
For negative arguments u
g
and v
g
are set equal to zero. The solution (20.67) may
be verified by substituting (20.67) into (20.66).
20.8 The equation of motion in Lagrangian enumeration coordinates
We will now return to Section 3.5 to express the equation of motion in terms of
the Lagrangian enumeration coordinates. We assume that we have frictionless flow
and apply the Cartesian coordinate system of the stereographic projection. The
transformation will be carried out with the help of Lagrange’s form of the equation
of motion.
We recall the transformation rule (M4.15) for covariant measure numbers of
vectors for the transformation from the Cartesian x
i
system to a general a
i
system.
In the present context the a
i
are the Lagrangian enumeration coordinates. This rule
is given by
A
a
k
= A
x
n
∂x
n
∂a
k
(20.68)
Application of this formula to the velocity results in
V
a
k
= V
x
n
∂x
n
∂a
k
(20.69)
where the Cartesian components (20.38) are given by
V
x
k
=
˙x
1
m
2
,
˙x
2
m
2
, ˙x
3
(20.70)
560 The stereographic coordinate system
Using the stringent metric simplification m = 1gives
V
a
k
= ˙x
n
∂x
n
∂a
k
(20.71)
It is also possible to use m = m(x
1
,x
2
) but the solution is more complicated and
less readily interpreted.
The contravariant basis vectors in the Cartesian and the Lagrangian system will
be arranged as
i
i
=
i
1
i
2
i
3
,
a
i
=
a
1
a
2
a
3
(20.72)
According to (M4.9) the transformation rule is given by
i
i
=
∂x
i
∂a
j
a
i
=
T
i
j
a
i
=
∂x
i
∂a
n
a
n
(20.73)
Here i and j denote the row and the column of the transformation matrix, respec-
tively. For the column of the basis vectors in the Lagrangian system we obtain the
following relation:
T
i
j
−1
=
∂x
i
∂a
j
−1
=
∂a
i
∂x
j
,
a
i
=
∂x
i
∂a
j
−1
i
i
(20.74)
Using the rules of matrix inversion, we find for the contravariant basis vector in the
Lagrangian system, see also (M3.14),
a
i
=
M
i
n
i
n
∂x
i
∂a
j
=
M
i
n
i
n
√
g
a
(20.75)
The M
j
i
are the elements of the adjoint matrix (M
i
j
)ofthetransformationmatrix
(T
i
j
).
In order to apply the Lagrangian form of the equation of motion, we need to find
an expression for the derivative of an arbitrary field function ψ with respect to the
enumeration coordinate a
k
. Recalling that ˙a
k
= 0, we may write
∂
˙
ψ
∂ ˙a
k
= lim
˙a
k
→0
∂
∂ ˙a
k
dψ
dt
= lim
˙a
k
→0
∂
∂ ˙a
k
∂ψ
∂t
a
k
+ ˙a
n
∂ψ
∂a
n
= δ
n
k
∂ψ
∂a
n
=
∂ψ
∂a
k
(20.76)
which is a very useful expression.
