Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


18.8 Problems 531
18.8 Problems
18.1: Perform in detail the steps involved in going from (18.65) to (18.68).
18.2: Show the steps involved in going from (18.78) to (18.79).
18.3: Express the Euler expansion d/dt with the help of covariant, contravariant,
and physical measure numbers of the velocity in the spherical coordinate system
with q
1
= λ, q
2
= ϕ,andq
3
= r.
18.4: Express the continuity equation for the rigid spherical coordinate system by
employing
(a) physi
cal measure numbers of the v
elocity, and
(b) contravariant measure numbers of the velocity.
18.5: Consider the spherical coordinate system shown in Figure 1.2. For rigid
rotation (v
D
= 0) the kinetic energy is given by
K
A
=
1
2
r
2
cos(
˙
λ + )
2
+ r
2
˙ϕ
2
+ ˙r
2
(a) From the metric fundamental quantities (see Section M4.2.1) find W
i
,W
j
,
k
ij
with
i, j, k = 1, 2, 3.
(b) Find the elements of the matrices (ω
ij
)and(ω
ij
*
).

19
The geographical coordinate system
In this chapter we will present the equation of motion and the continuity equation
in component form for the geographical coordinate system. This is a spherical
coordinate system that is rotating with constant angular velocity about the polar
axis ϕ = π/2. The horizontal coordinate lines to be used are the geographical
length λ and the geographical latitude ϕ. The vertical coordinate is taken as the
distance r from the center of the earth to the point under consideration. The
horizontal coordinate lines are curved but orthogonal to each other. The deformation
of coordinate surfaces will not be taken into account. A graphical representation of
the geographical system is shown in Figures 1.2 and 1.4 of Chapter 1.
19.1 The equation of motion
All we need do is employ the metric tensor as well as the velocity v
P
of the
geographical system in connection with the general formulations of the equations
of motion which we have presented in the previous chapter. The covariant forms of
the metric fundamental quantities have been derived previously; see (1.73). Since
we are dealing with an orthogonal coordinate system, we obtain the contravariant
form from the basic relation g
ii
= 1/g
ii
so that
g
11
= r
2
cos
2
ϕ, g
22
= r
2
,g
33
= 1,g
ij
= 0,i= j
g
11
=
1
r
2
cos
2
ϕ
,g
22
=
1
r
2
,g
33
= 1,g
ij
= 0,i= j
(19.1)
Of fundamental importance is the absolute kinetic energy K
A
of the system:
K
A
=
1
2
dr
dt
2
=
v
A
2
2
=
1
2
r
2
cos
2
ϕ
˙
λ
2
A
+ r
2
˙ϕ
2
A
+ ˙r
2
A
(19.2)
532
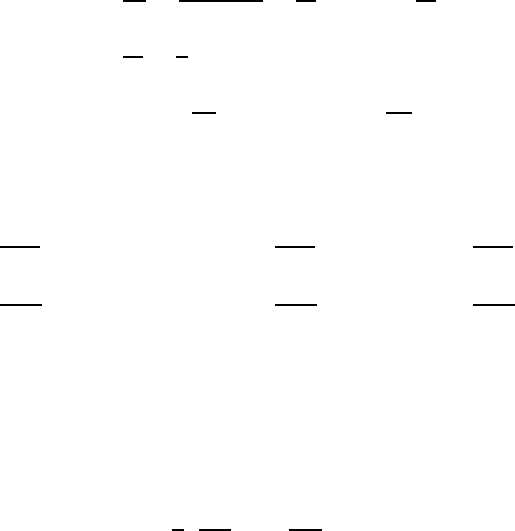
19.1 The equation of motion 533
where dr is taken from (1.72). The components of the contravariant velocity are
given by
˙q
1
A
=
˙
λ
A
=
˙
λ + , ˙q
2
A
= ˙ϕ
A
= ˙ϕ, ˙q
3
A
= ˙r
A
= ˙r
(19.3)
The angular velocity of the rotating system has been added to
˙
λ since we
are considering the motion in the absolute reference frame. The covariant and
contravariant components of the velocity v
P
= v
are then given by
W
1
= , W
2
= 0,W
3
= 0
W
1
= r
2
cos
2
ϕ, W
2
= 0,W
3
= 0
(19.4)
There is another way to obtain the metric fundamental quantities as well as
the components W
i
. According to (M4.38), the kinetic energy K
A
of the system
provides all the information which is needed. First we split K
A
into the kinetic
energy K of relative motion and the kinetic energy K
P
of the rotating system,
K
A
= K + K
P
,with
K
A
=
v
A
2
2
=
(v + v
P
)
2
2
=
v
2
2
+ v·v
P
+
v
2
P
2
K =
v
2
2
=
1
2
(r
2
cos
2
ϕ
˙
λ
2
+ r
2
˙ϕ
2
+ ˙r
2
)
K
P
= v·v
P
+
v
2
P
2
= r
2
cos
2
ϕ
˙
λ +
2
2
r
2
cos
2
ϕ
(19.5)
From these expressions we then obtain
g
11
=
∂
2
K
∂
˙
λ
2
= r
2
cos
2
ϕ, g
22
=
∂
2
K
∂ ˙ϕ
2
= r
2
,g
33
=
∂
2
K
∂ ˙r
2
= 1
W
1
=
∂K
P
∂
˙
λ
= r
2
cos
2
ϕ, W
2
=
∂K
P
∂ ˙ϕ
= 0,W
3
=
∂K
P
∂ ˙r
= 0
(19.6)
The covariant form of the equation of motion for rigid rotation is given by (18.25).
In order to evaluate this equation, we need to calculate the components of the tensor
ω
ij
as defined in (M5.48). Inspection shows that this tensor is antisymmetric or
skew-symmetric, as it is often called, so that
ω
ij
=
1
2
∂
∂q
i
W
j
−
∂
∂q
j
W
i
=−ω
ji
(19.7)

534 The geographical coordinate system
For consistency with our previous notation we put (q
1
,q
2
,q
3
) = (λ, ϕ, r). For ease
of reference we summarize the necessary components of the rotational tensor in
ω
11
= 0,ω
12
= r
2
cos ϕ sin ϕ, ω
13
=−r cos
2
ϕ
ω
21
=−ω
12
,ω
22
= 0,ω
23
= 0
ω
31
=−ω
13
,ω
32
= 0,ω
33
= 0
ω
k
i
= g
km
ω
im
,ω
*
ij
=
g
ii
g
jj
ω
ij
(19.8)
In order to write down the contravariant form of the equation of motion, we need
to specify the Christoffel symbols of the second kind whose definition is repeated
here:
k
ij
=
g
kn
2
∂g
in
∂q
j
+
∂g
jn
∂q
i
−
∂g
ij
∂q
n
=
k
ji
(19.9)
Even though the Christoffel symbols have the outward appearance of a tensor, they
do not obey the transformation laws for tensors. Nevertheless, it is still possible to
raise and lower the indices. In the most general case we would have 27 nonzero
Christoffel symbols. For orthogonal systems the easy but tedious computational
work is drastically reduced. For the geographical system the Christoffel symbols
are
1
11
= 0,
1
12
=−tan ϕ,
1
13
= 1/r
1
21
=
1
12
,
1
22
= 0,
1
23
= 0
1
31
=
1
13
,
1
32
= 0,
1
33
= 0
2
11
= cos ϕ sin ϕ,
2
12
= 0,
2
13
= 0
2
21
= 0,
2
22
= 0,
2
23
= 1/r
2
31
= 0,
2
32
=
2
23
,
2
33
= 0
3
11
=−r cos
2
ϕ
3
12
= 0,
3
13
= 0
3
21
= 0,
3
22
=−r,
3
23
= 0
3
31
= 0,
3
32
= 0,
3
33
= 0
(19.10)
Using the above information it is a simple task to write down the covariant form
of the equation of motion:
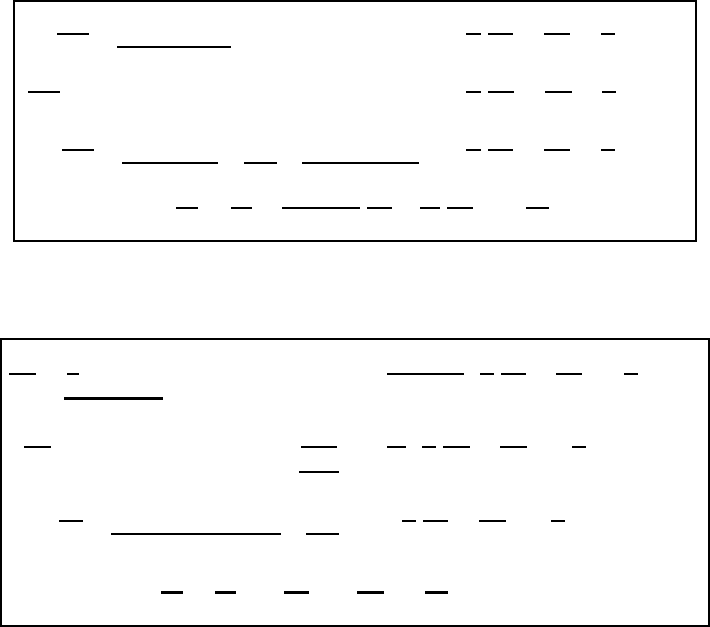
19.1 The equation of motion 535
dv
1
dt
+ 2r cos
2
ϕ ˙r − 2r
2
cos ϕ sin ϕ ˙ϕ =−
1
ρ
∂p
∂λ
−
∂φ
∂λ
+
1
ρ
q
λ
·∇ ·J
dv
2
dt
+ r
2
cos ϕ sin ϕ
˙
λ
2
+ 2r
2
cos ϕ sin ϕ
˙
λ =−
1
ρ
∂p
∂ϕ
−
∂φ
∂ϕ
+
1
ρ
q
ϕ
·∇ ·J
dv
3
dt
− r cos
2
ϕ
˙
λ
2
− r ˙ϕ
2
− 2r cos
2
ϕ
˙
λ =−
1
ρ
∂p
∂r
−
∂φ
∂r
+
1
ρ
q
r
·∇ ·J
d
dt
=
∂
∂t
+
v
1
r
2
cos
2
ϕ
∂
∂λ
+
v
2
r
2
∂
∂ϕ
+ v
3
∂
∂r
(19.11)
and the contravariant form:
d
˙
λ
dt
+
2
r
(
˙
λ + ) ˙r
− 2(
˙
λ + )tanϕ ˙ϕ =−
1
r
2
cos
2
ϕ
1
ρ
∂p
∂λ
+
∂φ
∂λ
+
1
ρ
q
λ
·∇ ·J
d ˙ϕ
dt
+ cos ϕ sin ϕ (
˙
λ + 2)
˙
λ +
2 ˙ϕ ˙r
r
=−
1
r
2
1
ρ
∂p
∂ϕ
+
∂φ
∂ϕ
+
1
ρ
q
ϕ
·∇ ·J
d ˙r
dt
− r cos
2
ϕ (
˙
λ + 2)
˙
λ − r ˙ϕ
2
=−
1
ρ
∂p
∂r
+
∂φ
∂r
+
1
ρ
q
r
·∇ ·J
d
dt
=
∂
∂t
+
˙
λ
∂
∂λ
+ ˙ϕ
∂
∂ϕ
+ ˙r
∂
∂r
(19.12)
just by following the general equations (18.25) and (18.34). The reader may decide
for himself which form he likes best and which set of equations seems easier to
use. It should be noted that the underlined terms are usually omitted in practi-
cal applications. The justification for omitting these terms will be given a little
later.
In equation (19.11) the leading terms are written as dv
i
/dt while the remaining
velocity variables appearing in this equation are (
˙
λ, ˙ϕ, ˙r). If it is desired to use the
contravariant components of the velocity (
˙
λ, ˙ϕ, ˙r) everywhere in this equation, we
may replace the v
i
by using the definitions
v
1
= g
1n
v
n
= r
2
cos
2
ϕ
˙
λ, v
2
= g
2n
v
n
= r
2
˙ϕ, v
3
= g
3n
v
n
= ˙r (19.13)
We will now derive the three components of the equation of motion in physical
coordinates. Since deformation of the coordinate surfaces is ignored (v
D
= 0) the
equation of motion in the form (18.37) may be applied. For the chosen geographical

536 The geographical coordinate system
coordinate system we have
v
*
k
=
√
g
kk
˙q
k
=⇒ v
*
1
= r cos ϕ
˙
λ, v
*
2
= r ˙ϕ, v
*
3
= ˙r
∂
∂q
*
k
=
1
√
g
kk
∂
∂q
k
=⇒
∂
∂q
*
1
=
1
r cos ϕ
∂
∂λ
,
∂
∂q
*
2
=
1
r
∂
∂ϕ
,
∂
∂q
*
3
=
∂
∂r
(19.14)
Recall that, in this particular system, there is no difference between covariant
and contravariant physical measure numbers. Using (19.8) and the information
(19.6) on the metric tensor g
ij
, it is a simple matter to obtain the component
equations in physical measure numbers by successively setting k = 1, 2, 3in
(18.37). Denoting the velocity components by v
*
1
= u, v
*
2
= v,andv
*
3
= w,
we obtain
du
dt
+
uw
r
−
uv
r
tan ϕ − fv+ lw =−
1
r cos ϕ
1
ρ
∂p
∂λ
+
∂φ
∂λ
+
1
ρ
e
λ
·∇ ·J
dv
dt
+
uw
r
+
u
2
r
tan ϕ + fu =−
1
r
1
ρ
∂p
∂ϕ
+
∂φ
∂ϕ
+
1
ρ
e
ϕ
·∇ ·J
dw
dt
−
(u
2
+ v
2
)
r
− lu =−
1
ρ
∂p
∂r
+
∂φ
∂r
+
1
ρ
e
r
·∇ ·J
d
dt
=
∂
∂t
+
u
r cos ϕ
∂
∂λ
+
v
r
∂
∂ϕ
+ w
∂
∂r
(19.15)
which is the most frequently used form of the equation of motion. For brevity we
have also introduced the Coriolis parameters f = 2 sin ϕ and l = 2 cos ϕ;see
Figure 1.4 and equation (1.81). It should be noted that the underlined terms are
usually omitted.
Certainly, it would have been possible to obtain the equation of motion in spheri-
cal coordinates from the vector equation directly, as we have already demonstrated
in Section 1.6 for physical measure numbers. However, by using the general forms
of the equation of motion derived in Chapter 18, we avoid entirely any problems
arising from the differentiation of the basis or unit vectors with respect to time and
space.
19.2 Application of Lagrange’s equation of motion
Now we wish to demonstrate how to obtain the components of the covariant form
of the equation of motion by using the powerful Lagrange formalism. At this point

19.2 Application of Lagrange’s equation of motion 537
it will be sufficient to demonstrate the method for k = 1. For this situation equation
(18.65) can be written as
d
dt
∂L
∂
˙
λ
−
∂L
∂λ
˙q
i
=−
1
ρ
∂p
∂λ
+
1
ρ
q
λ
·∇ ·J (19.16)
where the Lagrangian is given by
L = K
A
− φ
a
=
1
2
(r
2
cos
2
ϕ
˙
λ
2
+ r
2
˙ϕ
2
+ ˙r
2
+ 2r
2
cos
2
ϕ
˙
λ + r
2
cos
2
ϕ
2
) − φ
a
(19.17)
From this equation we easily find
∂L
∂
˙
λ
= r
2
cos
2
ϕ
˙
λ + r
2
cos
2
ϕ = v
1
+ r
2
cos
2
ϕ
∂L
∂λ
˙q
i
=−
∂φ
a
∂λ
=−
∂φ
∂λ
with φ = φ
a
− φ
z
= φ
a
−
2
2
r
2
cos
2
ϕ
(19.18)
which are then substituted into (19.16). With very little effort we find the equation
of motion for the covariant measure number v
1
:
dv
1
dt
+ 2r cos
2
ϕ ˙r − 2r
2
cos ϕ sin ϕ ˙ϕ =−
1
ρ
∂p
∂λ
−
∂φ
∂λ
+
1
ρ
q
λ
·∇ ·J (19.19)
which is, of course, identical with the first equation in (19.11).
In order to obtain the corresponding equation in physical measure numbers, we
transform (19.19). However, there may be situations in which it is preferable to use
(18.37) or even (18.36) when the deformation velocity v
D
cannot be ignored. To
transform (19.19) into physical velocity variables we use the relations
v
1
= r cos ϕu, ˙ϕ = v/r, ˙r = w (19.20)
Substitution of (19.20) into (19.19) gives
d
dt
(r cos ϕu) + lr cos ϕw− lr sin ϕv =−
1
ρ
∂p
∂λ
−
∂φ
∂λ
+
1
ρ
q
λ
·∇ ·J (19.21)
Simple differentiation of the first term finally results in the first equation of (19.15).
Similarly, we may use the Lagrange method to verify the remainder of (19.15).
538 The geographical coordinate system
19.3 The first metric simplification
Now we wish to explain the meaning of the underlined terms of the previous
equations. Observing that the vertical extent of the atmosphere is very small in
comparison with the radius a of the earth, it seems reasonable to introduce the
so-called first metric simplification. By this we mean that, in coordinate systems
having r or z as a vertical coordinate, we appear to be justified in replacing the
variable radius r by the fixed radius r = a whenever r appears in undifferentiated
form, i.e.
g
11
= a
2
cos
2
ϕ, g
22
= a
2
,g
33
= 1,g
ii
= 1/g
ii
,g
ij
= 0fori = j
(19.22)
This simply means that the components of the metric tensor g
ij
and g
ij
become
independent of height. From (19.22) it follows that
(dr)
2
= a
2
cos
2
ϕ (dλ)
2
+ a
2
(dϕ)
2
+ (dr)
2
(19.23)
Equations (19.22) and (19.23) describe a metric system in which various spherical
surfaces in the atmosphere, actually having different radii of curvature r, are forced
to assume the same radius of curvature a. This system cannot be visualized in
three-dimensional Euclidean space. We have already made some remarks on the
effect of this approximation in the appendix to Chapter 18.
The first metric simplification also leads to a change in the definition of the
absolute kinetic energy K
A
. Instead of (19.2) we now write
K
A
=
1
2
[a
2
cos
2
ϕ (
˙
λ
2
+ 2
˙
λ) + a
2
˙ϕ
2
+ ˙r
2
] +
1
2
a
2
cos
2
ϕ
2
(19.24)
and for the functional determinant
√
g =
g
ij
=
∂
2
K
A
∂ ˙q
i
∂ ˙q
j
= a
2
cos ϕ (19.25)
Specifically, if we were to repeat the derivations leading to equations (19.10),
(19.11), and (19.13), but using the g
ij
as stated in (19.22), the underlined terms
would not appear at all.
Comparison of equation (19.15), omitting the underlined terms, with equation
(2.26) shows that they are identical. Thus, the use of the first metric simplification
gives the same result as the scale analysis leading to (2.26). It should be noted,
however, that, in (2.26b), we have also ignored the latitudinal dependency of the
geopotential due to the assumption (1.83b).

19.4 The coordinate simplification 539
19.4 The coordinate simplification
In this section we wish to briefly review and elaborate the discussion on the
geopotential presented in Section 1.6. From the physical point of view it would
be desirable to replace the spherical coordinate system which we have used to
describe the atmospheric motion by another orthogonal coordinate system. This
new coordinate system should be adapted to the force fields of the rotating earth
in such a way that the vertical coordinate q
3
should follow the force lines resulting
from the gravitational attraction of the earth and from the centrifugal force.
In this system surfaces q
3
= constant would coincide with surfaces of constant
geopotential φ = φ
a
−
1
2
(
2
r
2
cos
2
ϕ), which may be well approximated by a
rotational ellipsoid of very small eccentricity. Such a surface φ = constant would
be the earth’s surface if it were not rigid, but instead had a freely movable surface
mass such as water, and if it were subjected only to the gravitational pull of the
earth and to the centrifugal force. The analytic consequence of this special idealized
surface would cause the horizontal derivatives of the geopotential to vanish.
Such an ideal coordinate system to describe the atmospheric motion would be a
spheroidal coordinate system, which is characterized by a rather complicated metric
tensor. The description of the metric fundamental quantities would then require the
specification of the geocentric latitude, see Figure 1.3, and the eccentricity of the
earth. Moreover, hyperbolic functions would arise in the description of the g
ii
instead of the trigonometric functions appearing in (19.1). However, the difference
between the geographical and the geocentric latitude is very small and it would
be very impractical to introduce an elliptic coordinate system to describe the flow
instead of the simple spherical coordinate system we have used so far. For this
reason we will continue to use the spherical coordinate system, but we retain the
advantage of the elliptic system by assuming that, in the relevant section of the
atmosphere, surfaces of φ = constant coincide with surfaces of r = constant.
Thus, the horizontal derivatives vanish:
∂φ
∂λ
= 0,
∂φ
∂ϕ
= 0 =⇒ φ = φ(r)(19.26)
Furthermore, we may assume that, in the region relevant to atmospheric weather
systems, the geopotential is a linear function of q
3
= r:
φ = gr + constant (19.27)
From this it follows that
∂φ
∂r
= g (19.28)
wherewetakeg = 9.81 m s
−1
as a sufficiently representative value. We will call
the approximations (19.26)–(19.28) the coordinate simplification.
540 The geographical coordinate system
19.5 The continuity equation
In the absence of deformation of the coordinate surfaces, v
D
= 0, the functional
determinant for the rigid rotation of the spherical coordinate system is given by
√
g = r
2
cos ϕ and the continuity equation in the form (18.48) is valid. Thus, we
immediately obtain
∂ρ
∂t
+
1
r
2
cos ϕ
∂
∂λ
(ρr
2
cos ϕ
˙
λ) +
∂
∂ϕ
(ρr
2
cos ϕ ˙ϕ) +
∂
∂r
(ρr
2
cos ϕ ˙r)
= 0
(19.29)
On combining the various terms we obtain the continuity equation with contravari-
ant velocity components in the form
1
ρr
2
cos ϕ
d
dt
(ρr
2
cos ϕ) +
∂
˙
λ
∂λ
+
∂ ˙ϕ
∂ϕ
+
∂ ˙r
∂r
= 0
with
d
dt
=
∂
∂t
+
˙
λ
∂
∂λ
+ ˙ϕ
∂
∂ϕ
+ ˙r
∂
∂r
(19.30)
By introducing the relations (19.14) into (19.29), we find the continuity equation
expressed in physical velocity components:
1
ρ
dρ
dt
+
1
r cos ϕ
∂u
∂λ
+
∂
∂ϕ
(v cos ϕ)
+
∂w
∂r
+
2w
r
= 0
with
d
dt
=
∂
∂t
+
u
r cos ϕ
∂
∂λ
+
v
r
∂
∂ϕ
+ w
∂
∂r
(19.31)
Suppose that we repeat the derivation of the continuity equation leading to
(19.30) but now using the first metric simplification. This simply means that we
replace r
2
by a
2
. In this case the functional determinant (19.25) must be used, so
equation (19.30) simplifies to the form
1
ρ cos ϕ
d
dt
(ρ cos ϕ) +
∂
˙
λ
∂λ
+
∂ ˙ϕ
∂ϕ
+
∂ ˙r
∂r
= 0
with
d
dt
=
∂
∂t
+
˙
λ
∂
∂λ
+ ˙ϕ
∂
∂ϕ
+ ˙r
∂
∂r
(19.32)
which is used in many practical applications. Finally, utilizing the first metric
simplification, equation (19.31) can be written as
1
ρ
dρ
dt
+
1
a cos ϕ
∂u
∂λ
+
∂
∂ϕ
(v cos ϕ)
+
∂w
∂r
= 0
with
d
dt
=
∂
∂t
+
u
a cos ϕ
∂
∂λ
+
v
a
∂
∂ϕ
+ w
∂
∂r
(19.33)
It can be seen that the term 2w/r in (19.31) has vanished in (19.33). This form is
also used for many practical applications.
