Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

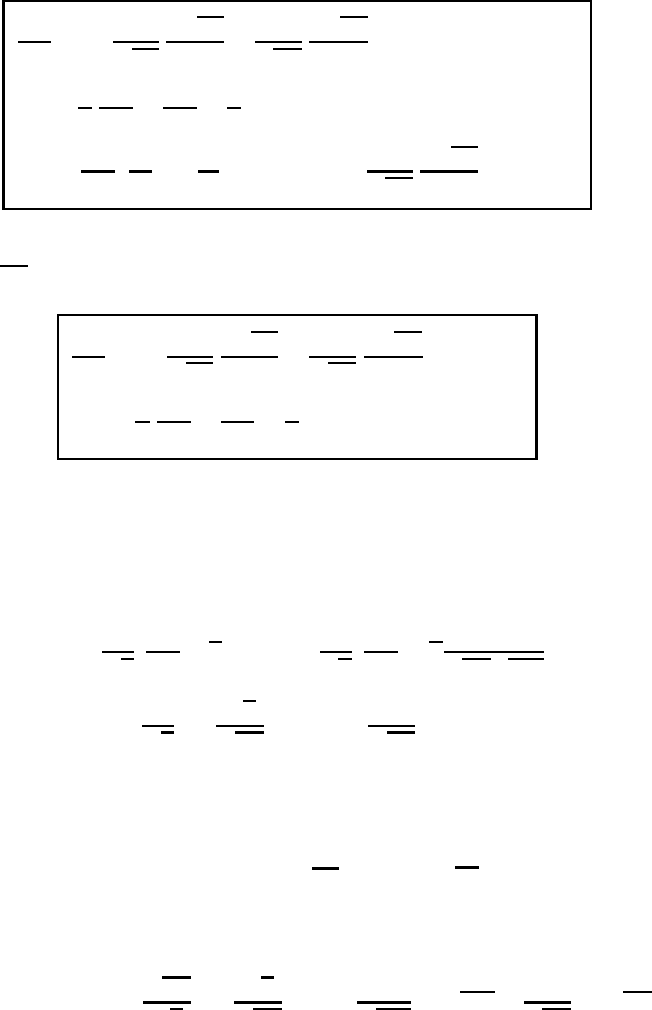
18.4 The equation of motion in orthogonal coordinate systems 521
into (18.23) gives the desired equation for orthogonal coordinate systems:
dv
*
k
dt
+ v
*
n
v
*
k
√
g
kk
∂
√
g
kk
∂q
*
n
−
v
*
n
√
g
nn
∂
√
g
nn
∂q
*
k
+ 2v
*
n
(ω
*
nk
+ ω
*
nk
D
)
=−
1
ρ
∂p
∂q
*
k
−
∂φ
∂q
*
k
+
1
ρ
e
k
·∇ ·J
+
∂
∂q
*
k
v
2
D
2
−
∂
∂t
W
k
D
*
− (v
*
k
+ W
k
D
*
)
1
√
g
kk
∂
√
g
kk
∂t
− 2W
n
D
*
ω
*
nk
(18.36)
If the relative system is moving like a rigid body then the terms involving v
D
and
∂
√
g
kk
/∂t vanish and we obtain
dv
*
k
dt
+ v
*
n
v
*
k
√
g
kk
∂
√
g
kk
∂q
*
n
−
v
*
n
√
g
nn
∂
√
g
nn
∂q
*
k
+ 2v
*
n
ω
*
nk
=−
1
ρ
∂p
∂q
*
k
−
∂φ
∂q
*
k
+
1
ρ
e
k
·∇ ·J
(18.37)
It will be observed that the expression in parentheses vanishes if n = k.This
simplifies equations (18.36) and (18.37) if they are written down separately for
k = 1, 2, 3.
It might be of interest to expand the frictional term as
e
k
·∇ ·J =
e
k
√
g
·
∂
∂q
n
√
gJ
nm
q
m
=
e
k
√
g
·
∂
∂q
n
√
g
J
*
nm
√
g
nn
√
g
mm
q
m
= e
k
·
1
√
g
∇
n
√
g
√
g
nn
J
*
nm
e
m
+
J
*
nm
√
g
nn
∇
n
e
m
(18.38)
by using the general divergence formula (M3.56). The last term involves the spatial
derivative of the unit vector e
j
which, according to (M4.45), can be written as
∇
j
e
i
= e
j
∇
*
i
√
g
jj
− δ
i
j
e
m
∇
*
m
√
g
ii
(18.39)
Using this equation in (18.38) yields
e
k
·∇ ·J = e
k
·e
m
√
g
nn
√
g
∇
*
n
√
g
√
g
nn
J
*
nm
+
J
*
mn
√
g
mm
∇
*
n
√
g
mm
−
J
*
nn
√
g
nn
∇
*
m
√
g
nn
(18.40)
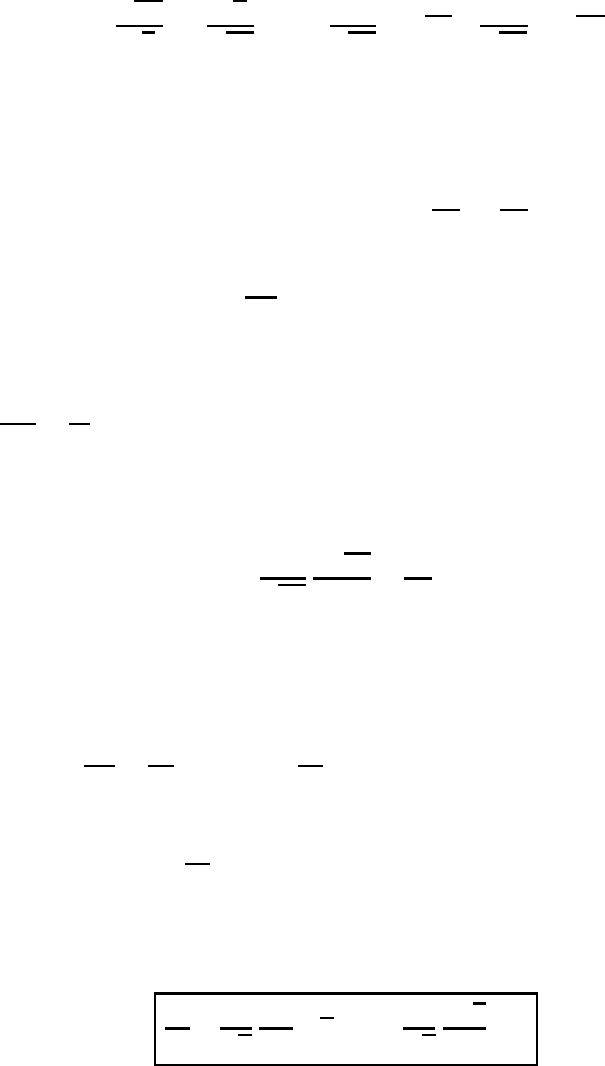
522 The equation of motion in general coordinate systems
so that the final form of the frictional term is given by
e
k
·∇ ·J =
√
g
nn
√
g
∇
*
n
√
g
√
g
nn
J
*
nk
+
J
*
kn
√
g
kk
∇
*
n
√
g
kk
−
J
*
nn
√
g
nn
∇
*
k
√
g
nn
(18.41)
Hence, if the form of the frictional dyadic and the metric tensor g
ij
are known we
can evaluate equation (18.41). However, for practical purposes one will often be
satisfied with simple parameterizations. If the measure numbers of the frictional
dyadic are given in Cartesian coordinates, we can transform these by well-known
rules to the general q
i
system.
Finally, we will briefly show that the term (1/
√
g
kk
) ∂
√
g
kk
/∂t contained in the
general form (18.36) of the equation of motion disappears if v
D
= 0. Starting with
∂q
i
∂t
=∇
i
v
P
= q
i
·∇v
P
(18.42)
and utilizing (M5.44), we can write for the local change with time of the metric
tensor g
ij
∂g
ij
∂t
=
∂
∂t
(q
i
·q
j
) = q
i
·(q
j
·∇v
P
) + q
j
·(q
i
·∇v
P
) = q
i
·v
P
∇·q
j
+ (q
i
·∇v
P
)·q
j
= q
i
·(∇v
P
+ v
P
∇)·q
j
= q
i
·2D
P
·q
j
= 2d
ij
(18.43)
Hence, the desired term of (18.36) can be written as
1
√
g
kk
∂
√
g
kk
∂t
=
d
kk
g
kk
(18.44)
showing that it is equal to zero if the deformational part
D
P
of the dyadic ∇v
P
vanishes due to (18.6).
The steps leading to the continuity equation in general coordinates are very
simple. From (M6.67) we have
Dρ
Dt
=
dρ
dt
+ ρ ∇·v
A
=
dρ
dt
+ ρ ∇·v + ρ ∇·v
P
= 0(18.45)
By expanding the individual derivative in the relative system we find
∂ρ
∂t
+ v·∇ρ + ρ ∇·v + ρ ∇·v
P
= 0(18.46)
On combining the second and third terms to give a divergence expression for the
quantity ρv and applying the general equation (M3.56) for the divergence, we find
the desired form of the continuity equation:
∂ρ
∂t
+
1
√
g
∂
∂q
n
(
√
g ˙q
n
ρ) +
ρ
√
g
∂
√
g
∂t
= 0
(18.47)
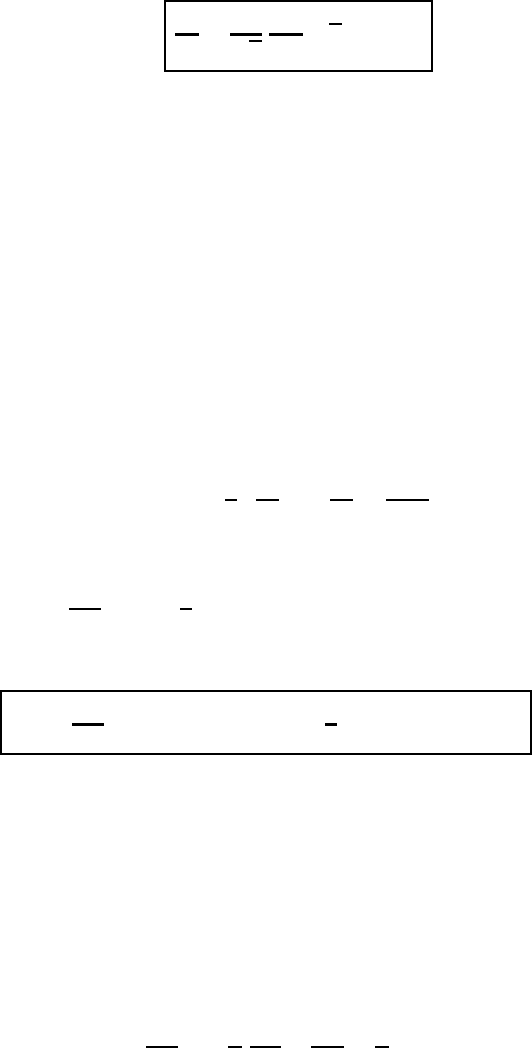
18.5 Lagrange’s equation of motion 523
For a rigid system the last term of (18.47) vanishes, resulting in the usual form
∂ρ
∂t
+
1
√
g
∂
∂q
n
(
√
g ˙q
n
ρ) = 0
(18.48)
which can be found in many textbooks.
18.5 Lagrange’s equation of motion
Another method for the representation of the covariant form of the equation of
motion is due to Lagrange. We will derive Lagrange’s equation of motion in the
form best suited for meteorological applications. The entire method is based on
knowledge of the absolute kinetic energy permitting the determination of the metric
fundamental quantitites and the velocity v
P
.
The starting point of the analysis is the well-known relation
(dr)
2
= g
mn
dq
m
dq
n
(18.49)
The kinetic energy per unit mass can be written as
K
A
=
1
2
dr
dt
2
=
v
2
A
2
=
˙x
n
˙x
n
2
(18.50)
in the absolute Cartesian coordinate system and as
K
A
=
g
mn
2
˙q
m
A
˙q
n
A
=
1
2
(g
mn
˙q
m
+ W
n
+ W
n
D
)( ˙q
n
+ W
n
+ W
n
D
)
(18.51)
in the general q
i
system. This expression may also be formulated as
K
A
=
g
mn
2
˙q
m
˙q
n
+ ˙q
n
(W
n
+ W
n
D
) +
1
2
v
2
+ v
2
D
+ W
m
W
m
D
(18.52)
since v
2
= W
n
W
n
and v
2
D
= W
n
D
W
n
D
. Inspection of (18.52) shows that the abso-
lute kinetic energy is a quadratic inhomogeneous form in the variables ˙q
i
.The
coefficients of the quadratic term are the metric fundamental quantities g
ij
;the
coefficients of the linear term are the covariant measure numbers W
k
and W
k
D
of
the velocity v
P
. The kinetic energy of the relative system appears as the separate
term (g
mn
/2) ˙q
m
˙q
n
.
The Lagrange equation will be derived by transforming the individual terms of
the absolute equation of motion
d ˙x
i
dt
=−
1
ρ
∂p
∂x
i
−
∂φ
a
∂x
i
+
1
ρ
i
i
·∇ ·J (18.53)
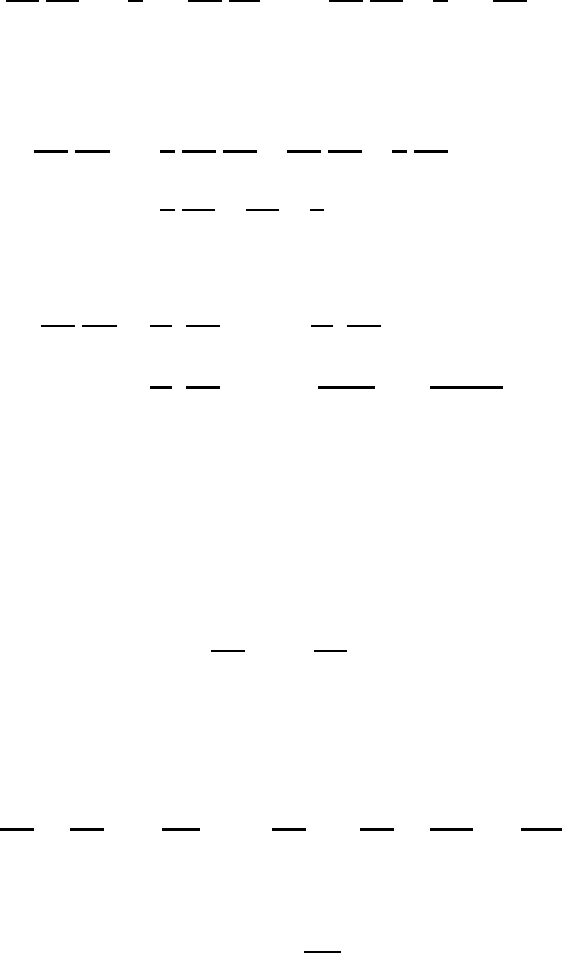
524 The equation of motion in general coordinate systems
expressed in the rectangular Cartesian system to the q
i
system. Now we apply
the method of contraction by multiplying the latter equation by ∂x
i
/∂q
k
and then
adding the result from i = 1toi = 3:
3
i=1
∂x
i
∂q
k
d ˙x
i
dt
=−
1
ρ
3
i=1
∂x
i
∂q
k
∂p
∂x
i
−
3
i=1
∂x
i
∂q
k
∂φ
a
∂x
i
+
1
ρ
3
i=1
∂x
i
∂q
k
i
i
·∇ ·J (18.54)
The same expression can also be written more briefly by applying the Einstein
summation rule:
∂x
n
∂q
k
d ˙x
n
dt
=−
1
ρ
∂x
n
∂q
k
∂p
∂x
n
−
∂x
n
∂q
k
∂φ
a
∂x
n
+
1
ρ
∂x
n
∂q
k
i
n
·∇·J
=−
1
ρ
∂p
∂q
k
−
∂φ
a
∂q
k
+
1
ρ
q
k
·∇ ·J
(18.55)
Let us rewrite the left-hand side as
∂x
n
∂q
k
d ˙x
n
dt
=
d
dt
∂x
n
∂q
k
˙x
n
− ˙x
n
d
dt
∂x
n
∂q
k
=
d
dt
∂x
n
∂q
k
˙x
n
− ˙x
n
∂
2
x
n
∂t ∂q
k
+ ˙q
m
∂
2
x
n
∂q
m
∂q
k
(18.56)
We will now attempt to introduce the kinetic energy K
A
, which is a function of ˙q
k
and q
k
. We need to recall that the metric tensor g
ij
and the measure numbers W
k
and
W
k
are functions of q
k
only. Implicitly the contravariant velocities ˙q
k
also depend
on q
k
and on the time t. In the Lagrange treatment the kinetic energy will be
considered as a function of the independent variables ˙q
k
and q
k
so that K
A
=
K
A
( ˙q
k
,q
k
,t). For clarity we also introduce the special partial derivative operator
∂
∂q
k
˙q
i
=
∂
∂q
k
˙q
1
, ˙q
2
, ˙q
3
(18.57)
indicating that the differentiation ∂/∂q
k
is performed for constant-velocity com-
ponents ˙q
1
, ˙q
2
, ˙q
3
. Using this convention, the last term in (18.56) can be rewritten
as
˙x
n
∂
∂q
k
˙q
i
∂x
n
∂t
+ ˙q
m
∂x
n
∂q
m
= ˙x
n
∂ ˙x
n
∂q
k
˙q
i
=
∂
∂q
k
˙q
i
˙x
n
˙x
n
2
=
∂K
A
∂q
k
˙q
i
(18.58)
The next step in the derivation is made easy by applying the transformation rule
A
x
k
=
∂x
k
∂q
m
A
q
m
(18.59)
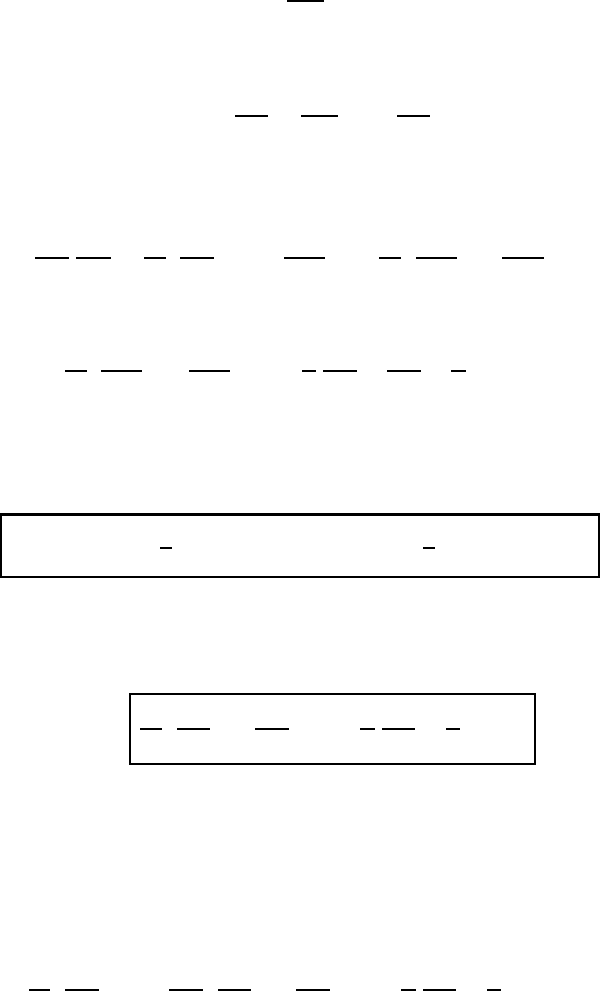
18.5 Lagrange’s equation of motion 525
which is repeated from (M4.15). On identifying A
k
as the measure number ˙x
k
of
the absolute velocity v
A
we obtain
˙x
k
=
∂x
k
∂q
m
( ˙q
m
+ W
m
)(18.60)
Next we differentiate ˙x
k
with respect to ˙q
i
:
∂ ˙x
k
∂ ˙q
i
=
∂x
k
∂q
m
δ
m
i
=
∂x
k
∂q
i
(18.61)
since ∂x
k
/∂q
m
and W
m
surely do not depend on ˙q
i
. Substituting this expression
together with (18.58) into (18.56) yields
∂x
n
∂q
k
d ˙x
n
dt
=
d
dt
∂ ˙x
n
∂ ˙q
k
˙x
n
−
∂K
A
∂q
k
˙q
i
=
d
dt
∂K
A
∂ ˙q
k
−
∂K
A
∂q
k
˙q
i
(18.62)
so (18.55) may be written as
d
dt
∂K
A
∂ ˙q
k
−
∂K
A
∂q
k
˙q
i
=−
1
ρ
∂p
∂q
k
−
∂φ
a
∂q
k
+
1
ρ
q
k
·∇ ·J (18.63)
Since the potential φ
a
of the gravitational attraction is assumed to be a function of
the position q
i
only, we may rewrite equation (18.63) by introducing the Lagrangian
function L, defined by
L = K
A
− φ
a
=
1
2
g
mn
˙q
m
˙q
n
+ ˙q
n
(W
n
+ W
n
D
) +
1
2
v
2
D
+ W
m
W
m
D
− φ
(18.64)
As usual, we have combined the potential of the gravitational attraction φ
a
with the
centrifugal potential φ
z
= v
2
/2 to give the geopotential φ = φ
a
− φ
z
representing
the effective gravitational force. Thus, we obtain
d
dt
∂L
∂ ˙q
k
−
∂L
∂q
k
˙q
i
=−
1
ρ
∂p
∂q
k
+
1
ρ
q
k
·∇ ·J (18.65)
which is known as Lagrange’s equation of motion in general coordinates or Lan-
grange’s equation of motion of the second kind. We must observe that the derivatives
∂L/∂ ˙q
k
and ∂L/∂q
k
|
˙q
i are again functions of ˙q
i
and q
i
.
Finally, we expand the individual time operator d/dt = ∂/∂t + ˙q
n
∂/∂q
n
,which
requires differentiations with respect to q
i
. Moreover, the velocity ˙q
i
must no longer
be considered a constant. On rewriting (18.65) in detail we find
∂
∂t
∂L
∂ ˙q
k
+ ˙q
n
∂
∂q
n
∂L
∂ ˙q
k
−
∂L
∂q
k
˙q
i
=−
1
ρ
∂p
∂q
k
+
1
ρ
q
k
·∇ ·J (18.66)

526 The equation of motion in general coordinate systems
The required derivatives
∂L
∂ ˙q
k
= g
mk
˙q
m
+ W
k
+ W
k
D
= v
k
+ W
k
+ W
k
D
(18.67)
and
∂L
∂q
k
˙q
i
=
˙q
m
˙q
n
2
∂g
mn
∂q
k
+ ˙q
n
∂
∂q
k
W
n
+ W
n
D
+
∂
∂q
k
v
2
D
2
+ W
n
∂
∂q
k
W
n
D
+ W
n
D
∂
∂q
k
W
n
−
∂φ
∂q
k
(18.68)
follow directly from (18.37). It will be observed that the metric fundamental quan-
tity g
ij
occurs twice since g
ij
= g
ji
, so the factor
1
2
no longer appears in (18.67).
We will now prove that Lagrange’s equation (18.65) is a special form of the
covariant equation of motion (18.23). We proceed by first taking the individual
time derivative of (18.67) to obtain
d
dt
∂L
∂ ˙q
k
=
dv
k
dt
+
∂
∂t
W
k
+ ˙q
n
∂
∂q
n
W
k
+
∂
∂t
W
k
D
+ ˙q
n
∂
∂q
n
W
k
D
(18.69)
With (18.68) and (18.69) the left-hand side of (18.65) can be written as
d
dt
∂L
∂ ˙q
k
−
∂L
∂q
k
˙q
i
=
dv
k
dt
−
˙q
m
˙q
n
2
∂g
mn
∂q
k
+ ˙q
n
∂
∂q
n
W
k
+W
k
D
−
∂
∂q
k
W
n
+W
n
D
+
∂φ
∂q
k
+
∂
∂t
W
k
D
−
∂
∂q
k
v
2
D
2
+
∂
∂t
W
k
− W
n
∂
∂q
k
W
n
D
− W
n
D
∂
∂q
k
W
n
(18.70)
According to (M5.47) the term in brackets is given by 2(ω
nk
+ ω
nk
D
). Furthermore,
the last three terms of (18.70) may be reformulated by means of (18.25), (18.27),
and (18.9), yielding 2W
n
D
ω
nk
. By substituting the resulting equation into (18.65)
we finally obtain
dv
k
dt
−
˙q
m
˙q
n
2
∂g
mn
∂q
k
+ 2 ˙q
n
(ω
nk
+ ω
nk
D
) =−
1
ρ
∂p
∂q
k
−
∂φ
∂q
k
+
1
ρ
q
k
·∇ ·J
+
∂
∂q
k
v
2
D
2
−
∂
∂t
W
k
D
− 2W
n
D
ω
nk
(18.71)
Comparison with the general covariant form of the equation of motion (18.23)
shows that these two equations are completely identical. The Langrange method is
very powerful, as we shall see from various applications to be described later.
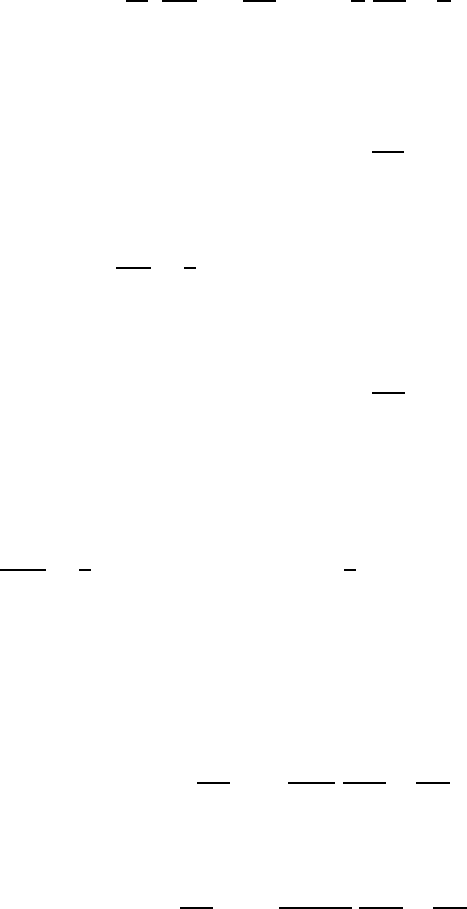
18.6 Hamilton’s equation of motion 527
18.6 Hamilton’s equation of motion
We conclude this chapter by briefly discussing Hamilton’s equation of motion.
Let us consider Lagrange’s equation in the form for absolute motion. In this case
(18.65) can be written as
d
dt
∂L
∂ ˙q
k
A
−
∂L
∂q
k
˙q
i
A
=−
1
ρ
∂p
∂q
k
+
1
ρ
q
k
·∇ ·J (18.72)
Now the components ˙q
i
A
,i= 1, 2, 3, are held constant when the differentiation
with respect to q
k
is carried out. Thus, the Lagrangian function is given by
L
˙q
k
A
,q
k
= K
A
˙q
k
A
,q
k
− φ
a
(q
k
) =
g
mn
2
˙q
m
A
˙q
n
A
− φ
a
(q
k
)(18.73)
from which it follows that
∂L
∂ ˙q
k
A
=
1
2
g
mn
δ
m
k
˙q
n
A
+ g
mn
δ
n
k
˙q
m
A
= g
kn
˙q
n
A
= ˙q
k,A
(18.74)
Let us now introduce the Hamiltonian function H , which is defined by
H ( ˙q
k,A
,q
k
) = K
A
( ˙q
k,A
,q
k
) + φ
a
(q
k
) =
g
mn
2
˙q
m,A
˙q
n,A
+ φ
a
(q
k
)(18.75)
To facilitate the operations we have expressed the kinetic energy K
A
in terms
of covariant velocity components. We now differentiate H with respect to the
covariant velocity component ˙q
k,A
and obtain
∂H
∂ ˙q
k,A
=
1
2
g
mn
δ
k
m
˙q
n,A
+ g
mn
δ
k
n
˙q
m,A
=
1
2
g
kn
˙q
n,A
+ g
km
˙q
m,A
= ˙q
k
A
(18.76)
This results in the contravariant velocity component ˙q
k
A
which appears in the kinetic
energy used in the Lagrange function L in (18.73).
Next we find from (18.73) the derivative of L with respect to q
k
,wherethe
contravariant velocity component ˙q
i
A
is held constant. This yields
∂L
∂q
k
˙q
i
A
=
˙q
m
A
˙q
n
A
2
∂g
mn
∂q
k
−
∂φ
a
∂q
k
(18.77)
Holding the covariant velocity constant, we find from (18.75)
∂H
∂q
k
˙q
i,A
=
˙q
m,A
˙q
n,A
2
∂g
mn
∂q
k
+
∂φ
a
∂q
k
(18.78)
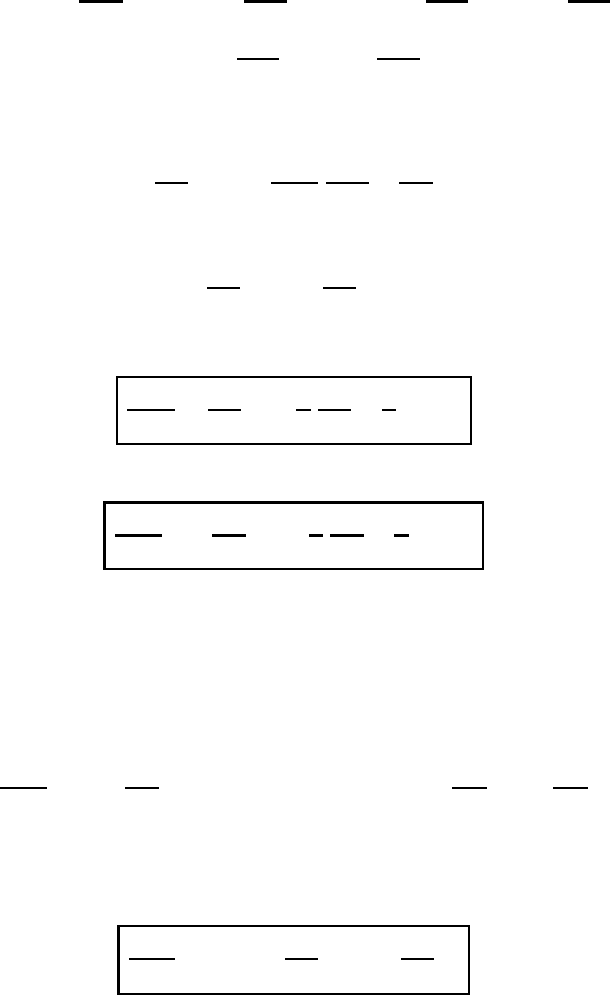
528 The equation of motion in general coordinate systems
So far we have not found any important relation between L and H .Inorderto
discover these, we reformulate the first term on the right-hand side of (18.78) with
the help of well-known relations, giving
˙q
m,A
˙q
n,A
∂g
mn
∂q
k
= ˙q
r
A
g
mr
˙q
s,A
∂g
ms
∂q
k
=−˙q
r
A
˙q
s,A
g
ms
∂g
mr
∂q
k
=−˙q
r
A
˙q
m
A
∂g
mr
∂q
k
since g
mr
g
ms
= δ
s
r
=⇒
∂g
mr
∂q
k
g
ms
+ g
mr
∂g
ms
∂q
k
= 0
(18.79)
Therefore, equation (18.78) can be rewritten in the form
∂H
∂q
k
˙q
i,A
=−
˙q
m
A
˙q
n
A
2
∂g
mn
∂q
k
+
∂φ
a
∂q
k
(18.80)
Comparison of this equation with (18.77) gives the desired relation
∂H
∂q
k
˙q
i,A
=−
∂L
∂q
k
˙q
i
A
(18.81)
Substituting (18.74) into (18.72) gives Lagrange’s form of the equation of
motion:
d ˙q
k,A
dt
=
∂L
∂q
k
˙q
i
A
−
1
ρ
∂p
∂q
k
+
1
ρ
q
k
·∇ ·J
(18.82)
Finally, with the help of (18.81), we obtain Hamilton’s form of the equation of
motion:
d ˙q
k,A
dt
=−
∂H
∂q
k
˙q
i,A
−
1
ρ
∂p
∂q
k
+
1
ρ
q
k
·∇ ·J
(18.83)
We now look at the same problem from a different point of view. Using the
basic definitions of L and H stated in (18.73) and (18.75), we find the relationship
between H and L.Sincetheg
ij
depend on q
k
and ˙q
A,k
= g
kn
˙q
n
A
we may also write
H = 2K
A
− L = g
mn
˙q
m
A
˙q
n
A
− L
˙q
k
A
,q
k
= ˙q
n,A
˙q
n
A
− L
˙q
k
A
,q
k
(18.84)
Let us consider H as a function of ( ˙q
A,k
,q
k
). Then the variation of H results in
δH =
∂H
∂ ˙q
n,A
δ ˙q
n,A
+
∂H
∂q
n
˙q
i,A
δq
n
= ˙q
n,A
δ ˙q
n
A
+ ˙q
n
A
δ ˙q
n,A
−
∂L
∂ ˙q
n
A
δ ˙q
n
A
−
∂L
∂q
n
˙q
i
A
δq
n
(18.85)
Here the first and the third term on the right-hand side cancel out according to
(18.74). Inspection of the latter equation shows that
∂H
∂ ˙q
k,A
= ˙q
k
A
,
∂H
∂q
k
˙q
i,A
=−
∂L
∂q
k
˙q
i
A
(18.86)
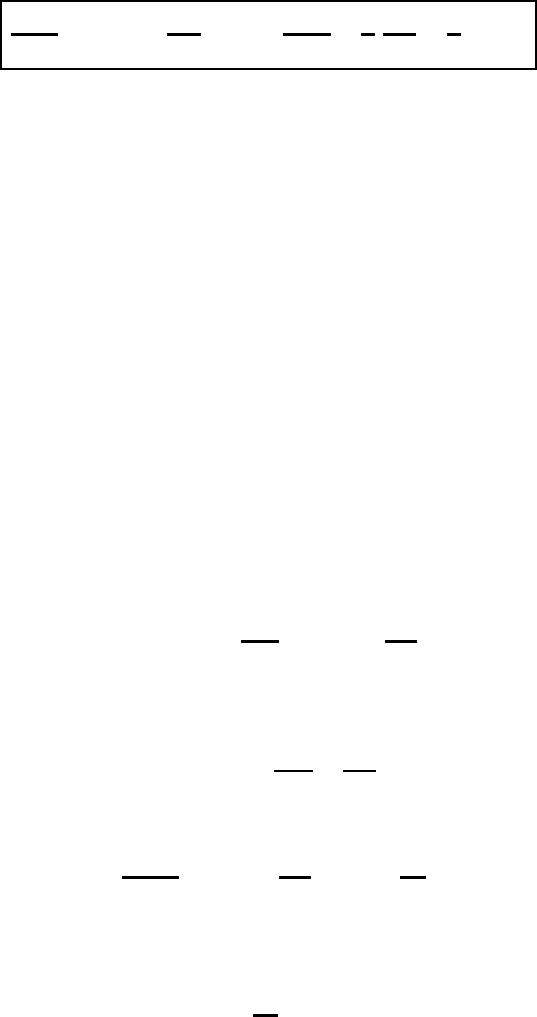
18.6 Hamilton’s equation of motion 529
thus verifying the relations (18.76) and (18.81).
Equations (18.76) and (18.83),
∂H
∂ ˙q
k,A
= ˙q
k
A
,
∂H
∂q
k
˙q
i,A
=−
d ˙q
k,A
dt
−
1
ρ
∂p
∂q
k
+
1
ρ
q
k
·∇ ·J
(18.87)
are known as Hamilton’s canonical equations of motion. They consist of 2n first-
order differential equations whereas Lagrange’s equation consists of n second-
order differential equations. In our case n = 3. The velocity component ˙q
k,A
may
be considered as the momentum for unit mass. Hamilton’s canonical equations are
very general and hold for the case that the potential-energy function also depends
on ˙q
k
(the tidal problem) and for systems in which L explicitly depends on time,
but in these cases the total energy is no longer necessarily H .
In our furture work we will have many opportunities to work with Lagrange’s
equation of motion, but we refrain from using the Hamilton formulation, which
is an extremely important tool in quantum mechanics. In our work the Hamilton
formulation has no decisive advantage over the Lagrange method. A very simple but
illuminating example will be given next in order to obtain Hamilton’s equations of
motion for the one-dimensional harmonic oscillator. The equation of the harmonic
oscillator is of great importance in many branches of physics and in physical
meteorology, but it will usually be obtained by elementary considerations.
Recalling that there is no difference between covariant and contravariant coor-
dinates in the Cartesian system, H assumes a particularly simple form. Since we
are not dealing with unit mass, we write for the kinetic energy K
A
and the potential
energy V
K
A
=
m ˙x
2
2
,V=
kx
2
2
(18.88)
where m is the mass of the oscillating particle and k is Hooke’s constant.Nowthe
Hamiltonian function is given by
H =
m ˙x
2
2
+
kx
2
2
(18.89)
resulting in Hamilton’s equations of motion as
∂H
∂(m ˙x)
= ˙x,
∂H
∂x
˙x
i
=−m
d ˙x
dt
= kx (18.90)
The first expression is simply an identity while the second expression is the well-
known equation of the harmonic oscillator:
m
d ˙x
dt
+ kx = 0(18.91)

530 The equation of motion in general coordinate systems
18.7 Appendix
The material of this appendix is not essential for understanding the following chap-
ters and may therefore be omitted. However, it helps us to grasp the consequences
of the metric simplification which will be introduced soon.
Let us form the Riemann–Christoffel tensor or the covariant curvature tensor.
First we form the covariant expression ∇
i
(∇
j
A
k
) −∇
j
(∇
i
A
k
), where A
k
is any
covariant tensor of rank 1. For the first term, according to Section M5.6, we may
write
∇
i
(∇
j
A
k
) =∇
i
(∇
j
A
k
) − (∇
m
A
k
)
m
ij
− (∇
j
A
m
)
m
ik
=∇
i
(∇
j
A
k
− A
n
n
jk
) −
m
ij
(∇
m
A
k
− A
n
n
mk
) −
m
ik
(∇
j
A
m
− A
n
n
jm
)
=∇
i
(∇
j
A
k
) −
n
jk
∇
i
A
n
− A
n
∇
i
n
jk
−
m
ij
∇
m
A
k
+ A
n
m
ij
n
mk
−
m
ik
∇
j
A
m
+ A
n
m
ik
n
jm
(18.92)
The second term is found by interchanging the free indices i and j . We obtain
∇
j
(∇
i
A
k
) =∇
j
(∇
i
A
k
) −
n
ik
∇
j
A
n
− A
n
∇
j
n
ik
−
m
ji
∇
m
A
k
+ A
n
m
ji
n
mk
−
m
jk
∇
i
A
m
+ A
n
m
jk
n
im
(18.93)
Next we subtract (18.93) from (18.92). The underlined terms cancel out since
k
ij
=
k
ji
and due to the fact that ∇
i
∇
j
=∇
j
∇
i
. Thus, we obtain
∇
i
(∇
j
A
k
)−∇
j
(∇
i
A
k
) = A
n
(
m
ik
n
jm
−∇
i
n
jk
−
m
jk
n
im
+∇
j
n
ik
) = A
n
R
n
kij
(18.94)
The expression
R
l
kij
=
m
ik
l
jm
−∇
i
l
jk
−
m
jk
l
im
+∇
j
l
ik
(18.95)
is known as the Riemann–Christoffel tensor or the curvature tensor.
In the Cartesian coordinate system we obviously have R
l
kij
= 0. Thus, in the
Euclidean space the interchange rule
∇
i
∇
j
=∇
j
∇
i
(18.96)
is valid. In atmospheric dynamics we often use simplified metric forms resulting
from the assumption that the radius of the earth–atmosphere system is equal to the
mean radius of the earth itself. By assuming that the atmosphere has zero vertical
extent we are leaving the Euclidean metric. Therefore, there exists no relation
between the q
i
coordinates of the chosen system and the Cartesian coordinates,
so q
i
= q
i
(x
1
,x
2
,x
3
,t). In this case the curvature tensor does not vanish and the
interchange rule (18.96) concerning the covariant derivatives is no longer valid.
