Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

16.7 The principle of geostrophic adjustment 491

Let us now consider the tendencies of u, φ,andv at the central point y = 0as

the time t approaches inﬁnity. The result is

(a)

∂u

∂t



t→∞

= 0, (b)

∂φ

∂t



t→∞

= 0, (c)

∂v

∂t



t→∞

= 0(16.102)

For the stationary values u

∞

= u(y,t →∞), v

∞

= v(y,t →∞), and φ

∞

φ(y,t →∞), characterized by vanishing partial derivatives with respect to time,

we ﬁnd

∞

=−

∂φ

∞

∂y

∞

= 0,φ

∞

= φ

∞

(y)

(16.103)

Owing to the assumption that only the space variable y is considered, φ

∞

must be

independent of x. If this were not the case v

∞

would differ from zero. The important

point to observe is that, in case of stationarity, we have geostrophic balance.

In order to evaluate u

∞

, we must derive the proﬁle function for φ

∞

. We proceed

by observing that the system (16.84) has an invariant. This follows simply by

combining parts (16.84a) and (16.84c) and by treating the Coriolis parameter as a

constant. The result is

∂

∂t



∂u

∂y

+ f



= 0(16.104)

from which it follows that

∂u

∂y

+ f

= constant (16.105)

The similarity to the potential vorticity deﬁned by equation (10.149) is apparent.

Application of the conservation theorem (16.105) for the cases t →∞and t = 0

gives

∞

+ f

∞

+ f

φ(y,0)

(16.106)

With Rossby we introduce the characteristic length L

= φ

1/2

/f (16.107)

now known as the Rossby deformation radius, and we obtain the second-order

ordinary differential equation

∞

−

∞

=−f

−

φ(y,0)

(16.108)

492 Rossby waves

This differential equation can be solved by specifying proper conditions involving

u and the geopotential φ. On applying the conditions

φ(y,0) = 0

≤∞

∞

(y) = 0

→∞

u(y) =



≥ L



1 + cos(πy/L)



(16.109)

where U and L are ﬁxed values of velocity and length, equation (16.108) transforms

to give

∞

−

∞



≥ L

(πUf/L)sin(πy/L)

(16.110)

The eigenvalues (characteristic values) of the homogeneous part of (16.110) are

given by ±L

, so the general solution of the homogeneous part of this differential

equation can be written down immediately. The particular solution



∞

may be

found using the method of undetermined coefﬁcients by choosing a solution of the

type of the right-hand side of (16.110)



∞

= A sin



πy



=⇒ A =−

πLUf

+ L

(16.111)

wherein the constant A has been obtained by substituting



∞

into (16.110). For the

various segments on the y-axis we obtain the complete solution as

∞

(y) =







B exp(−y/L

) y ≥ L

C exp(y/L

) y ≤−L

D exp(y/L

) + E exp(−y/L

) +



∞

(16.112)

The various integration constants can be found from the requirement that φ

∞

and

∂φ

∞

/∂y are continuous at y =±L. They are given by

B =−C = πA

sinh





D =−E =

πA

exp



−



(16.113)

Inspection of the integration constants shows that the ratio L/L

plays a dominant

role. Therefore, we are going to consider two asymptotic cases. For the stationary

velocity ﬁeld we obtain

∞

=−

∂φ

∞

∂y



0 L  L

u(y) L  L

(16.114)

16.8 Appendix 493

Hence, for t →∞we obtain for the limited line segment L  L

that the

initial and ﬁnal velocity ﬁelds nearly coincide. For L  L

the ﬁnal velocity

ﬁeld is mainly dominated by the mass ﬁeld which is represented by the stationary

geopotential. The veriﬁcation of the latter equation is left as an exercise.

Several sections of this chapter quite closely follow Panchev (1985) and also

Pichler (1997) in slightly modiﬁed form.

16.8 Appendix

In this appendix we brieﬂy derive the Fourier transform of a derivative and of the

constant A. The Fourier transform v

(y,t) of the partial derivative ∂v(y,t)/∂y is

given by

v

,t) =



∞

−∞

∂v(y,t)

∂y

exp(−ik

y) dy

= v(y, t)exp(−iky)



∞

−∞

+ ik



∞

−∞

v(y,t)exp(−ik

y) dy

(16.115)

Assuming that v(y,t)vanishesaty =±∞,

lim

y→±∞

v(y,t) = 0(16.116)

the transform of the partial derivative of v(y,t) is given by the second term on the

right-hand side of (16.116). Generalizing, we obtain for the nth derivative of the

function v(y,t)

v

,t) = (ik

)

v(k

,t)(16.117)

provided that all the integrated parts vanish at y =±∞.

If the function v(y,t) is speciﬁed as

v(y) =



≤ a

(16.118)

the Fourier transform is given by

v(k

) = A



−a

exp(−ik

y) dy =

A[exp(ik

a) − exp(−ik

a)]

2A sin(k

= 0

(16.119)

494 Rossby waves

16.9 Problems

16.1: Assume that the stream function

ψ(x,y, t) =−u

y + A sin(ay + ε) + B sin[k

(x − ct − µy )]

satisﬁes the nonlinear divergence-free vorticity equation. Which conditions must

be satisiﬁed? The basic current is expressed by the ﬁrst two terms on the right-hand

side of the above equation. Find an expression for the velocity of the zonal basic

current.

16.2: Show that the static stability can be written as

∂

∂p

κp

∂φ

∂p

with κ =

16.3: Derive equation (16.55).

16.4: Prove that equation (16.71) is equivalent to equation (16.72).

16.5: Verify equation (16.73) for n = 2.

16.6: Verify equation (16.102). Show that (16.102b) is independent of Y .Toverify

(16.102c), make a proper transformation.

16.7: Solve the differential equation (16.110) subject to the conditions (16.109) to

verify the solution (16.112).

16.8: Verify equation (16.114) for the section

<Ldeﬁned by equation

(16.112).

Inertial and dynamic stability

In Sections 17.1–17.3 we consider inertial frictionless horizontal motion of an

air parcel in a basic zonal geostrophic ﬂow ﬁeld. Dynamic-stability criteria for

atmospheric motions are derived in Sections 17.4–17.7. The criteria for inertial

and dynamic stability will be derived by means of the so-called air-parcel-dynamic

method. This method considers an isolated air parcel that is subjected to a virtual

displacement that leaves the state variables of the basic ﬁeld undisturbed. The air

pressure acting on the parcel is assumed to be identical with the air pressure of the

unperturbed surroundings.

17.1 Inertial motion in a horizontally homogeneous pressure ﬁeld

The simplest case is frictionless horizontal inertial motion in a homogeneous

pressure ﬁeld. In this case the basic current is absent. The horizontal components

of the equation of motion on the tangential plane, assuming that we have a constant

Coriolis parameter f

, are given by

− f

v = 0

u +

= 0







− f















= 0(17.1)

We shall ﬁnd the solution of this system by application of the operator method,

converting the system (17.1) into a second-order differential equation:



+ f











= 0(17.2)

495

496 Inertial and dynamic stability

Because of the positive sign in front of f

we have the well-known vibrational

differential equation with the general solution

u = A cos(f

t) + B sin(f

v = C cos(f

t) + D sin(f

(17.3)

The frequency of the vibrational motion is often called the inertial frequency:

ω = 2π/τ = f

(17.4)

τ is the period of the vibration. To evaluate the four constants and to ﬁnd the

trajectory we choose as initial conditions

t = 0: x = x

,u= 0; y = y

= 0,v= v

(17.5)

Using (17.5) we ﬁnd from (17.3) and the differential equations of the ﬂow

A = D = 0,B= v

,C= v

(17.6)

The solution to (17.2) is then given by

u = v

sin(f

t),v= v

cos(f

t)(17.7)

Integration over time yields

x − x

[1 − cos(f

t)],y=

sin(f

t)(17.8)

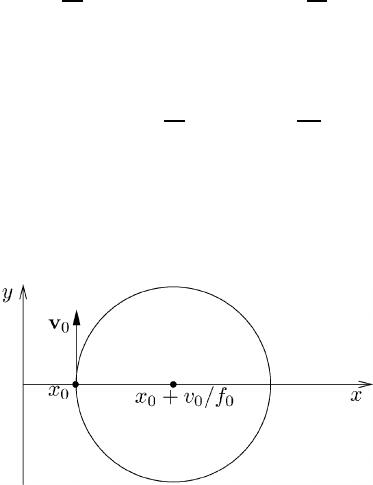
Elimination of the time dependency by squaring (17.8) results in the trajectory of

the inertial motion:



x −





+ y

(17.9)

which is depicted in Figure 17.1. This ﬁgure represents circular anticyclonic motion

of inertial frequency f

. This type of motion is known as the circle of inertia.By

necessity the motion is stable since the air parcel returns to its initial position.

Fig. 17.1 The trajectory of an air parcel with vanishing pressure gradient, inertial motion.

17.2 Inertial motion in a homogeneous geostrophic wind ﬁeld 497

Fig. 17.2 A homogeneous geostrophic wind ﬁeld.

17.2 Inertial motion in a homogeneous geostrophic wind ﬁeld

In contrast to the previous section, we assume the existence of a constant geostrophic

air current. An isolated air parcel embedded in it is subjected to a virtual displace-

ment. Owing to the parcel-dynamic condition, the pressure existing within the

moving air parcel is identical to that of the unperturbed surroundings. The situation

is depicted in Figure 17.2.

The equation of motion of the isolated air parcel, in constrast to (17.1), is now

given by

− u) + f

v = 0, −f

− u) +

= 0(17.10)

since the geostrophic wind is assumed to be constant. Application of the operator

method gives



+ f







− u





= 0(17.11)

Again we ﬁnd a differential equation of pure vibration of inertial frequency ω = f

whose general solution is given by

− u = A cos(f

t) + B sin(f

t),v= C cos(f

t) + D sin(f

t)(17.12)

We apply the initial conditions

t = 0: x = x

,u= u

; y = y

= 0,v= v

(17.13)

to obtain the integration constants and the trajectory. From (17.12) and the differ-

ential equation of the ﬂow ﬁeld we ﬁnd

A = D = 0,B=−v

,C= v

(17.14)

yielding

u = u

+ v

sin(f

t),v= v

cos(f

t)(17.15)

498 Inertial and dynamic stability

Integration over time leads to

x − x

= u

t +

[1 − cos(f

t)],y=

sin(f

t)(17.16)

This parametric representation of the trajectory of the isolated air parcel can be

transformed onto a moving (ξ,y)-coordinate system in which the ξ -axis is displaced

in the positive x-direction with the geostrophic velocity u

. The new coordinate ξ

is then given by

ξ = x − u

t with ξ (t = 0) = ξ

= x

(17.17)

In the moving system equation (17.16) reads

ξ = ξ

[1 − cos(f

t)],y=

sin(f

t)(17.18)

Elimination of the time dependency results in the circular trajectory



ξ −





+ y

(17.19)

in the moving coordinate frame. Backward transformation to the resting coordinate

system yields a cycloid as the trajectory for the inertial motion of the isolated air

parcel as a superposition of the circular motion and the uniform basic air current.

Again we have a stable inertial motion since the motion repeats itself.

17.3 Inertial motion in a geostrophic shear wind ﬁeld

17.3.1 Stability considerations

We now consider the inertial motion of an isolated parcel of air in a basic geostrophic

ﬂow of horizontal shear u

= u

(y) as shown in Figure 17.3.

The horizontal equations of motion for the particle velocity (u, v) assuming the

parcel-dynamic condition are given by

− f

v = 0,

+ f

(u − u

) = 0(17.20)

Fig. 17.3 A geostrophic shear wind ﬁeld.

17.3 Inertial motion in a geostrophic shear wind ﬁeld 499

We may introduce the invariant quantity I into the u-component equation by

means of

−f

v =

−f

(u−f

y) =

= 0 with I = u−f

y (17.21)

showing that, for the perturbed motion of the air parcel, the quantity I is individually

conserved. Correspondingly, for the basic current we deﬁne the quantity

I = u − f

y or I

= u

− f

y (17.22)

The isolated air parcel is displaced latitudinally from its original position some-

where on the x-axis at x = x

and y = y

= 0 to position y. If it does not return to

its original position we observe the case of inertial instability. We conclude from

(17.21) that the displaced particle retains its invariant quantity I of the original

position at y = 0, which is I

(0), or

I (y) = I (0) = I

(0) (17.23)

In the undisturbed surroundings at position y, however, we have

(y) ≈ I

(0) +

(0)y (17.24)

From the above equations it follows immediately that

u(y) − u

(y) = I (y) − I

(y) =−

(0)y (17.25)

This expression will be introduced into the equation of motion (17.20). Before

doing so we will introduce the deﬁnition of the absolute geostrophic vorticity η

With v

= 0wehave

= ζ

+ f

=−

∂u

∂y

+ f

(17.26)

From (17.22) we ﬁnd

−

(0) =−

∂u

∂y

(0) + f

= η

(0) (17.27)

Owing to the assumption about the geostrophic wind ﬁeld the relative vorticity is

a pure shear vorticity. Equation (17.25) can now be written as

u(y) − u

(y) = η

(0)y (17.28)

500 Inertial and dynamic stability

On introducing this expression into the v-component of the equation of motion

(17.20) we obtain a differential equation for the perturbed motion in the y-direction:

+ f

(u − u

) =

+ f

(0)y = 0(17.29)

whose well-known solution properties are

(0)



>0 vibration solution stable inertial motion

=0 transition the indifferent case

<0 exponential solution unstable inertial motion

(17.30)

To make the physical interpretation easier, this stability criterion will be rewritten

with the help of the relative shear vorticity (17.27) as

∂u

∂y

(0)



stable inertial motion

the indifferent case

unstable inertial motion

(17.31)

This criterion states that inertial instability occurs only if the anticyclonic wind

shear of the basic geostrophi

c current exceeds a critical value. This effect

is often

observed at the southern edge of the jet stream.

17.3.2 Determination of the trajectories

Since u

= u

(y) we have from the Taylor expansion (discontinued after the linear

term)

(y) = u

(0) +

∂u

∂y

(0)y,

= v

∂u

∂y

(0) =−vζ

(0) (17.32)

so that the u-component of the equation of motion (17.20) can be written as

(u − u

) − (ζ

(0) + f

)v = 0, where ζ

(0) + f

= η

(0) (17.33)

By applying the operator method to the set consisting of (17.33) and the

v-component of (17.20) we obtain at once



+ ω







u − u





= 0 with ω

= f

(0) (17.34)

The general solution is given by

u − u

= A cos(ωt) + B sin(ωt),v= C cos(ωt) + D sin(ωt)(17.35)