Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


17.7 Sectorial stability and instability with permanent adaptation 511
potential temperature θ. Ertel (1943) approached the stability problem in a different
way by giving up the requirement that I is invariant. Instead, he assumed that
the quantity I of the perturbed motion permanently assumed the value I of the
basic field at each position. The truth probably lies between the assumptions of
invariance and the permanent adaptation. Ertel’s assumption simplifies equation
(17.50), which now reads
d
2
s
dt
2
=−(θ − θ)
∂
∂s
(17.86)
Using (17.51) and (17.52), the differential equation for the perturbed motion is
given by
d
2
s
dt
2
−
∂θ
∂s
(0)
∂
∂s
s = 0(17.87)
The solution properties of this equation are given by
∂
θ
∂s
(0)
∂
∂s
<0 dynamic stability
=0 the indifferent case
>0 dynamic instability
(17.88)
We consider two examples.
(i) Vertical
displacement,
s = z − z
0
. Because ∂/∂z < 0wemust
have
∂
θ/∂z > 0 for dynamic stability.
(ii) We consider two ar
bitrary directions
s
1
and s
2
of displacement in the (y,z)-plane as
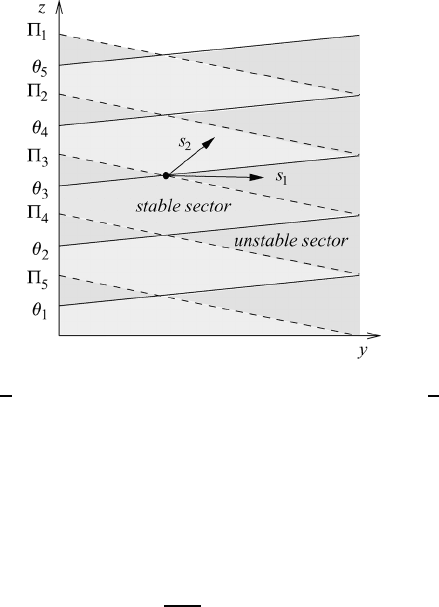
shown in Figure 17.7. Indifference lines are isentropes and lines of constant Exner
functions. Displacement s
1
results in dynamic instability whereas displacement s
2
represents dynamic stability. The figure refers to average conditions in the tropospheric
west-wind region.
In case of permanent adaptation of the quantity I to average field conditions
the unstable sector is located between isentropes and lines of = constant. For a
useful physical interpretation of Ertel’s theory we are compelled to borrow a result
from the general circulation theory. Let us designate rising motion by the vertical
velocity ω
< 0inthep system. In case of southerly flow we expect heating θ
> 0.
For the production of kinetic energy we must have
θ
ω
< 0(17.89)
where the primed quantities refer to the deviation of properly defined mean values
and the overbar refers to the average of the correlation. Equation (17.89) states
that rising motion must be accompanied by heating. This requirement is satisfied
by displacement s
1
so that dynamic instability is coupled with the production of
512 Inertial and dynamic stability
Fig. 17.7 Sectors of stability and instability in case of permanent adaptation. Unstable
displacement s
1
: ∂θ/∂s < 0,∂/∂s < 0; stable displacement s
2
: ∂θ/∂s > 0,∂/
∂s < 0.
kinetic energy. The situation differs in case of the stable displacement s
2
.Herethe
advective temperature change due to southerly flow is overcompensated by a very
strong rising air current (ω
< 0) causing a cooling effect (θ
< 0). Therefore, a
stable dynamic displacement s
2
due to
θ
ω
> 0(17.90)
is connected with a reduction of the kinetic energy of the flow. For further details
on the theory of stability see Ertel et al. (1941).
17.8 Problems
17.1: Perform in detail all steps between equations (17.35) and (17.38).
17.2: Discuss the special case η
g
(0) = 0, see equation (17.34), and find the trajec-
tory. Express your answer in the moving coordinate system.
17.3: Show in detail the steps involved in going from (17.60) to (17.63).
17.4: Derive equation (17.81).
18
The equation of motion in general coordinate systems
18.1 Introduction
The numerical investigation of specific meteorological problems requires the selec-
tion of a suitable coordinate system. In many cases the best choice is quite obvious.
Attempts to use the same coordinate system for entirely different geometries usu-
ally introduce additional mathematical complexities, which should be avoided. For
example, it is immediately apparent that the rectangular Cartesian system is not
well suited for the treatment of problems with spherical symmetry. The inspection
of the metric fundamental quantities g
ij
or g
ij
and their derivatives helps to decide
which coordinate system is best suited for the solution of a particular problem. The
study of the motion over irregular terrain may require a terrain-following coordi-
nate system. However, it is not clear from the beginning whether the motion is best
described in terms of covariant or contravariant measure numbers. We will discuss
this situation later.
From the thermo-hydrodynamic system of equations consisting of the dynamic
equations, the continuity equation, the heat equation, and the equation of state we
will direct our attention mostly toward the equation of motion using covariant and
contravariant measure numbers. We will also briefly derive the continuity equation
in general coordinates. In addition we will derive the equation of motion using
physical measure numbers and assuming that the curvilinear coordinate lines are
orthogonal.
The starting point of the analysis is the equation of motion in the absolute
coordinate system. The description of the motion in a rotating and time-dependent
coordinate system, in general, requires knowledge of the rotational velocity of a
point in the atmosphere as well as the deformation velocity of the material surface
on which the point is located. Finally, we must compute the velocity of an air parcel
relative to this point. For further details review Chapter 1.
513
514 The equation of motion in general coordinate systems
In order to obtain the general form of the equation of motion, it is very con-
venient to use the method of covariant differentiation. The reader who is not
familiar with this method may find the necessary mathematical background in
Chapter M5.
18.2 The covariant equation of motion in general coordinate systems
Before proceeding with the derivation of the equation of motion in covariant coor-
dinates, it will be best to present some useful expressions that will be needed later.
We begin the discussion by writing down the individual derivative of the rotational
part of v
P
in the absolute and the relative coordinate systems. In contrast to the
invariant individual derivative which is independent of any particular coordinate
system, the local derivative does depend on the coordinate system. The local time
derivative ∂v
/∂t in the absolute coordinate system is zero, as was shown in (1.45).
Therefore, it follows from
dv
dt
=
∂v
∂t
x
i
+ v
A
·∇v
= (v
P
+ v)·∇v
=
∂v
∂t
q
i
+ v·∇v
(18.1)
that the local time derivative of the rotational part of the motion in the general q
i
system is given by
∂v
∂t
q
i
=
∂v
∂t
= v
P
·∇v
(18.2)
and in terms of measure numbers by
∂
∂t
W
m
q
m
= W
n
q
n
·q
r
∇
r
W
m
q
m
with W
i
= W
i
+ W
i
D
(18.3)
On applying the rules of covariant differentiation followed by scalar multiplication
by q
k
, we obtain
∂
∂t
W
k
= W
n
∇
n
W
k
(18.4)
Using this relation together with (M5.17) and splitting W
i
, we immediately find
the expression
∂
∂t
W
k
= W
n
∇
k
W
n
+ W
n
∇
n
W
k
= W
n
∇
k
W
n
+ W
n
∇
k
W
n
D
+ W
n
∇
n
W
k
+ W
n
D
∇
n
W
k
= W
n
∇
k
W
n
D
+ W
n
D
∇
n
W
k
+ W
n
( ∇
n
W
k
+∇
k
W
n
)
(18.5)
18.2 The covariant equation of motion in general coordinate systems 515
which is not yet in the form most useful to our analysis. Since ∇v
is an antisym-
metric dyadic we recognize at once that
∇v
+
∇v
= q
m
q
n
(∇
m
W
n
+∇
n
W
m
) = 0 =⇒ ∇
i
W
j
+∇
j
W
i
= 0(18.6)
so that the expression in parentheses of (18.5) vanishes. Additionally, with the help
of (M5.4) and (M5.6), we find that the remaining part of equation (18.5) may be
formulated as
∂
∂t
W
k
= W
n
∇
k
W
n
D
+ W
n
D
∇
n
W
k
= W
n
(∇
k
W
n
D
+ W
r
D
n
rk
) + W
n
D
(∇
n
W
k
− W
r
r
nk
)
(18.7)
The two parts involving the Christoffel symbols add up to zero:
W
n
W
r
D
n
rk
− W
n
D
W
r
r
nk
= 0(18.8)
which is most easily recognized by interchanging the summation symbols n and r
in the second term. We have finally found the important relation
∂
∂t
W
k
= W
n
∇
k
W
n
D
+ W
n
D
∇
n
W
k
(18.9)
which is very useful to our work. In fact, it should be observed that the local
time derivative of W
k
does not vanish if the deformation velocity of the coordinate
surfaces differs from zero. Otherwise, in the absence of deformation, ∂W
k
/∂t = 0.
We begin the derivation of the equation of motion in covariant measure numbers
by writing down the equation of absolute motion, which is repeated for convenience
from (1.11):
dv
A
dt
=−
1
ρ
∇p −∇φ
a
+
1
ρ
∇·
J (18.10)
with v
A
= q
n
(v
n
+ W
n
). The covariant individual time derivative follows immedi-
ately:
q
n
dv
A,n
dt
= q
n
d
v
n
dt
+
d
W
n
dt
=−
1
ρ
q
n
∂p
∂q
n
− q
n
∂φ
a
∂q
n
+
1
ρ
∇·
J (18.11)
Scalar multiplication of this equation by the covariant basis vector q
k
gives
d
v
A,k
dt
=
d
v
k
dt
+
d
W
k
dt
=−
1
ρ
∂p
∂q
k
−
∂φ
a
∂q
k
+
1
ρ
q
k
·∇·J (18.12)
With the help of (M5.40) we may write
d
v
k
dt
=
∂v
k
∂t
+ v
n
∇
n
v
k
− v
n
v
m
m
kn
− v
n
∇
k
W
n
(18.13)
The term involving the Christoffel symbol can be rewritten in a more convenient
manner simply by employing the rules of raising and lowering the appropriate
indices. This yields
v
n
v
m
m
kn
= v
n
g
mr
v
r
m
kn
= v
n
v
r
knr
= v
n
v
m
knm
=
1
2
v
n
v
m
∂g
nm
∂q
k
(18.14)
516 The equation of motion in general coordinate systems
where use of (M3.40) has been made. By combining the first and the second term
on the right-hand side of (18.13) to give the individual acceleration, we may finally
write for the covariant derivative
d
v
k
dt
=
dv
k
dt
−
1
2
v
n
v
m
∂g
nm
∂q
k
− v
n
∇
k
W
n
(18.15)
The second term on the right-hand side is known as the metric acceleration since
it involves the metric fundamental quantities. This fictitious acceleration does not
result from the interaction of an air particle with other bodies but rather stems from
the particular choice of the coordinate system which is used to describe the motion
of the particle.
Next we must find suitable expressions for the individual time derivatives of the
measure numbers W
k
measuring the acceleration of a point P in the q
i
-coordinate
system that is moving with the velocity v
P
relative to the absolute system. In the
previous sections we have already set up the relationships which are needed. With
the help of (M5.39) we obtain immediately
d
W
k
dt
=
d
dt
W
k
+
d
dt
W
k
D
=
∂
∂t
W
k
+
∂
∂t
W
k
D
+ v
n
∇
n
W
k
+ v
n
∇
n
W
k
D
(18.16)
On replacing the covariant time derivatives by means of (M5.37) we find
d
W
k
dt
=
∂
∂t
W
k
− W
n
D
∇
k
W
n
− W
n
∇
k
W
n
D
+
∂
∂t
W
k
D
− W
n
D
∇
k
W
n
− W
n
D
∇
k
W
n
D
+ v
n
∇
n
W
k
+ v
n
∇
n
W
k
D
(18.17)
By utilizing (M5.49) the last two terms in (18.17) can be rewritten as
v
n
(∇
n
W
k
+∇
n
W
k
D
) = 2v
n
(ω
nk
+ ω
nk
D
) + v
n
(∇
k
W
n
+∇
k
W
n
D
)
= 2v
n
(ω
nk
+ ω
nk
D
) + v
n
(∇
k
W
n
+∇
k
W
n
D
)
(18.18)
where the final step resulted from raising and lowering of indices, and the fact
that the metric fundamental quantities may be treated as constants in covariant
differentiation.
Again by raising and lowering indices and by renaming them whenever needed,
we find without any difficulty
W
n
∇
k
W
n
=∇
k
(W
n
W
n
) − W
n
∇
k
W
n
=∇
k
(W
n
W
n
) − W
n
∇
k
W
n
=⇒ W
n
∇
k
W
n
=∇
k
W
n
W
n
2
=∇
k
v
2
2
=∇
k
v
2
2
(18.19)
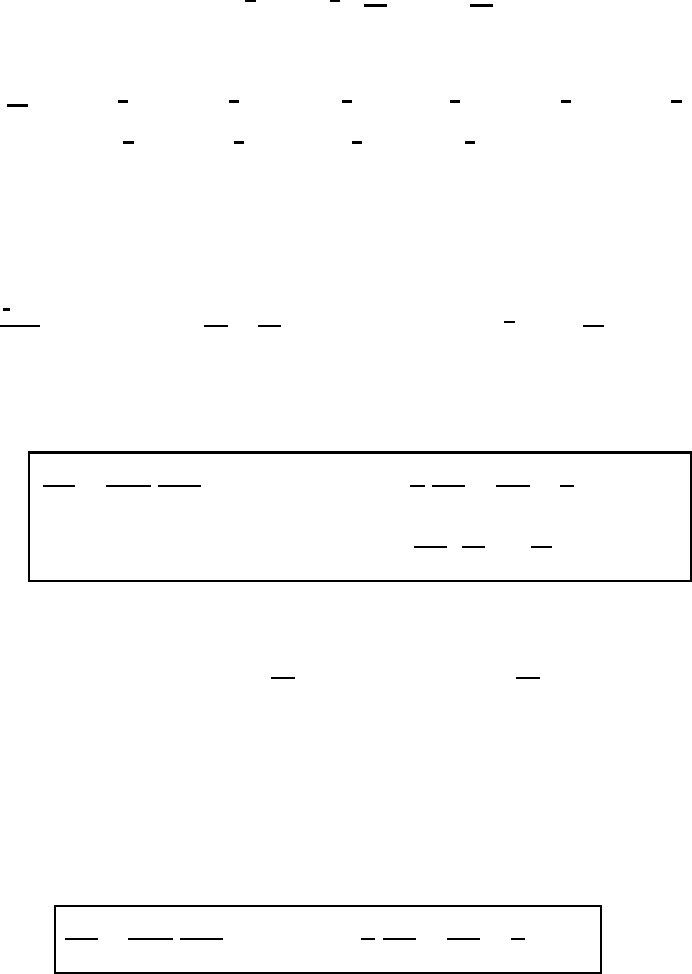
18.2 The covariant equation of motion in general coordinate systems 517
In this expression we have used the facts that v
2
/2 is a scalar field function and
that, for any scalar field function, the ordinary and covariant differential operators
are identical since no basis vector needs to be extracted. By applying identical
operations we find
W
n
D
∇
k
W
n
D
=∇
k
v
2
D
2
=∇
k
v
2
D
2
(18.20)
We may now combine the following three terms occurring in (18.17) as
∂
∂t
W
k
− W
n
∇
k
W
n
D
−W
n
D
∇
k
W
n
=W
n
D
∇
n
W
k
+W
n
∇
k
W
n
D
−W
n
∇
k
W
n
D
−W
n
D
∇
k
W
n
= W
n
D
∇
n
W
k
− W
n
D
∇
k
W
n
= W
n
D
∇
n
W
k
− W
n
D
∇
k
W
n
= 2W
n
D
ω
nk
(18.21)
Here we have replaced the local time derivative of W
k
with the help of (18.7) and
have used the defining relation (M5.48) for ω
ij
. On substituting (18.19), (18.20),
and (18.21) into (18.17) we obtain for the individual covariant time derivative of W
k
dW
k
dt
= 2W
n
D
ω
nk
−∇
k
v
2
2
+
v
2
D
2
+2v
n
(ω
nk
+ω
nk
D
) +v
n
∇
k
W
n
+
∂
∂t
W
k
D
(18.22)
Expressions (18.15) and (18.22) are now used in (18.11), yielding the covariant
form of the equation of relative motion with repect to a general time-dependent
coordinate system:
dv
k
dt
−
v
n
v
m
2
∂g
mn
∂q
k
+ 2v
n
(ω
nk
+ ω
nk
D
) =−
1
ρ
∂p
∂q
k
−
∂φ
∂q
k
+
1
ρ
q
k
·∇ ·J
+
∂
∂q
k
v
2
D
2
−
∂
∂t
W
k
D
− 2W
n
D
ω
nk
(18.23)
where the geopotential φ has been introduced according to
φ = φ
a
−
v
2
2
= φ
a
+ φ
z
,φ
z
=−
v
2
2
(18.24)
Closer inspection of this equation shows that several terms also contain contravari-
ant coordinates. Since the leading term, i.e. the individual time derivative dv
k
/dt,
contains the covariant velocity v
k
, the entire equation is called the covariant form
of the equation of motion.
Finally we consider an important simplification by requiring that the coordi-
nate lines are rigid so that the deformation velocity v
D
= 0. In this case (18.23)
reduces to
dv
k
dt
−
v
n
v
m
2
∂g
mn
∂q
k
+ 2v
n
ω
nk
=−
1
ρ
∂p
∂q
k
−
∂φ
∂q
k
+
1
ρ
q
k
·∇ ·J
(18.25)
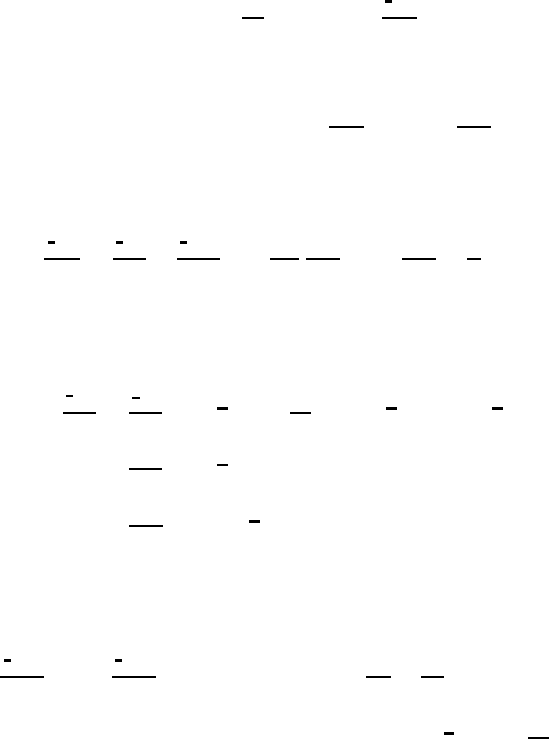
518 The equation of motion in general coordinate systems
In some cases the covariant equation may be less convenient for practical appli-
cations than its contravariant counterpart. In the following section we are going to
derive the contravariant form of the equation of relative motion. Which of these
two equations is more easily applied can be decided by inspecting the metric
fundamental quantities g
ij
or g
ij
and their derivatives.
18.3 The contravariant equation of motion in general coordinate systems
The derivation of the contravariant representation of relative motion follows the
procedure of the previous section. We begin the derivation by stating the individual
change with time of the absolute velocity in terms of the contravariant measure
number v
k
A
d
dt
v
n
A
q
n
= q
n
dv
n
A
dt
(18.26)
The components of the gradient operator appearing as part of the individual time
derivative are
∇=q
m
∇
m
= q
m
∂
∂q
m
= g
mn
q
m
∂
∂q
n
(18.27)
The equation of absolute motion (18.10) in terms of the contravariant measure
number v
k
A
is given analogously to (18.12) by
d
v
k
A
dt
=
d
v
k
dt
+
d
W
k
dt
=−
g
nk
ρ
∂p
∂q
n
− g
nk
∂φ
a
∂q
n
+
1
ρ
q
k
·∇ ·J (18.28)
The next step is to derive an expression for the individual covariant change with
time of the contravariant relative velocity v
k
. Application of (18.11), (18.16), and
(M5.4) results in
d
v
k
dt
=
∂v
k
∂t
+ v
n
∇
n
v
k
=
∂
∂t
v
k
+ v
n
∇
n
W
k
+ v
n
∇
n
v
k
=
∂v
k
∂t
+ v
n
∇
n
W
k
+ v
n
∇
n
v
k
+ v
n
v
m
k
nm
=
dv
k
dt
+ g
km
v
n
∇
n
W
m
+ v
n
v
m
k
nm
(18.29)
The covariant derivative of the contravariant measure numbers W
k
will not be
derived anew but will be found more briefly by raising the covariant index. Utilizing
(18.22) we find
d
W
k
dt
= g
km
dW
m
dt
=g
km
2W
n
D
ω
nm
−∇
m
v
2
2
+
v
2
D
2
+ g
km
2v
n
(ω
nm
+ ω
nm
D
) + v
n
∇
m
W
n
+
∂
∂t
W
m
D
(18.30)
By application of the addition theorem of the velocities in the form v
k
A
= v
k
+W
k
,
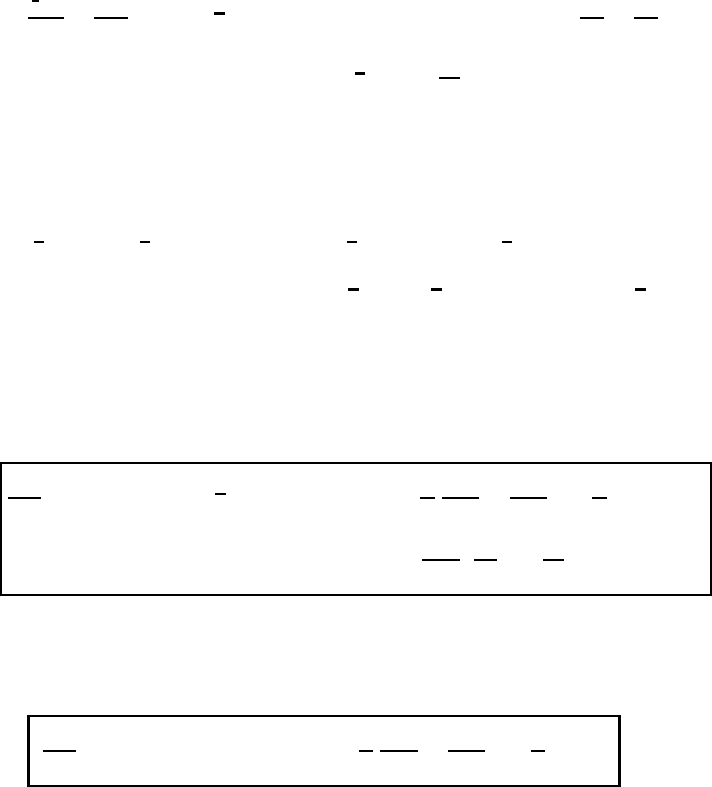
18.3 The contravariant equation of motion in general coordinate systems 519
we obtain from (18.29) and (18.30)
d
v
k
A
dt
=
dv
k
dt
+ g
km
v
n
∇
n
W
m
+ v
n
v
m
k
nm
+ g
km
2W
n
D
ω
nm
−∇
m
v
2
2
+
v
2
D
2
+ g
km
2v
n
(ω
nm
+ ω
nm
D
) + v
n
∇
m
W
n
+
∂
∂t
W
m
D
(18.31)
Utilizing (M5.49) and (18.6), three of the terms occurring on the right-hand side
of this expression may be combined according to
v
n
∇
n
W
m
+ v
n
∇
m
W
n
+ 2v
n
ω
nm
D
= v
n
∇
n
(W
m
+ W
m
D
) +∇
m
(W
n
+ W
n
D
) + 2ω
nm
D
= v
n
∇
n
W
m
D
+∇
m
W
n
D
+ 2ω
nm
D
= 2v
n
∇
n
W
m
D
(18.32)
Substitution of (18.31) together with (18.32) into (18.28) yields the final form
of the contravariant equation of motion for a general time-dependent coordinate
system:
dv
k
dt
+ v
m
v
n
k
mn
+ 2v
n
(∇
n
W
k
D
+ ω
k
n
) =−g
km
1
ρ
∂p
∂q
m
+
∂φ
∂q
m
+
1
ρ
q
k
·∇ ·J
+ g
km
∂
∂q
m
v
2
D
2
−
∂
∂t
W
m
D
− 2W
n
D
ω
nm
(18.33)
For the special case of a rigid system the deformation velocity vanishes, so the
above equation reduces to
dv
k
dt
+ v
m
v
n
k
mn
+ 2v
n
ω
k
n
=−g
km
1
ρ
∂p
∂q
m
+
∂φ
∂q
m
+
1
ρ
q
k
·∇ ·J
(18.34)
Summarizing, we may state that with equations (18.23) and (18.33) we have
obtained the components of the equation of motion in covariant and contravariant
representations in a very general form. We may apply these forms to any time-
dependent coordinate system. No restriction has been made regarding the velocity
v
P
. If we wish to write down the equation of motion in a particular coordinate sys-
tem, all we must do is procure information about the metric fundamental quantities
g
ij
or g
ij
and the velocity v
P
. If this information is available, we are in a position to
write down at once the components of the equation of motion either in the covariant
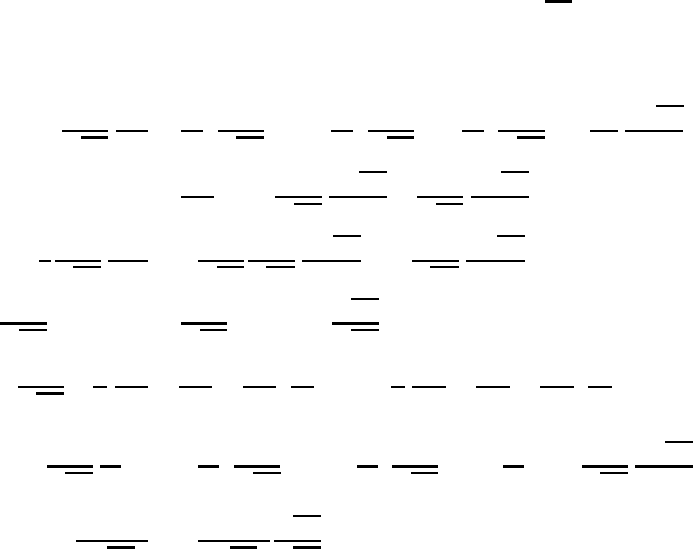
520 The equation of motion in general coordinate systems
or in the contravariant form. Thus, the laborious method of obtaining the component
representation of the equation of motion for each coordinate system separately can
be entirely avoided. Which system is simpler to use for the numerical solution
depends on the metric fundamental quantities and on the final form of the equation.
In the next chapters we will gain some practice in applying the various coordinate
systems.
18.4 The equation of motion in orthogonal coordinate systems
In this section we are going to assume that the q
i
-coordinate lines form an orthog-
onal system so that g
ij
= 0,i= j ,andg
ii
g
ii
= 1. Whenever orthogonal systems
are used it is customary and useful to introduce the physical measure numbers
since there is no difference between covariant and contravariant physical measure
numbers. Furthermore, unit vectors will be employed instead of basis vectors. We
will transform the covariant form of the equation of motion (18.23) into physical
measure numbers.
The way we proceed is to multiply (18.23) by the factor 1/
√
g
kk
. For clarity we
transform each term of (18.23) separately. All mathematical steps are summarized
in
1
√
g
kk
dv
k
dt
=
d
dt
v
k
√
g
kk
− v
k
d
dt
1
√
g
kk
=
d
dt
v
k
√
g
kk
+
v
k
g
kk
d
√
g
kk
dt
=
dv
*
k
dt
+ v
*
k
1
√
g
kk
∂
√
g
kk
∂t
+
v
*
n
√
g
kk
∂
√
g
kk
∂q
*
n
−
1
2
v
n
v
n
√
g
kk
∂g
nn
∂q
k
=−
v
n
v
n
√
g
kk
g
nn
√
g
nn
∂
√
g
nn
∂q
k
=−
v
*
n
v
*
n
√
g
nn
∂
√
g
nn
∂q
*
k
2v
n
√
g
kk
(ω
nk
+ ω
nk
D
) =
2v
n
√
g
kk
(ω
nk
+ ω
nk
D
)
√
g
nn
√
g
nn
= 2v
*
n
(ω
*
nk
+ ω
*
nk
D
)
1
√
g
kk
−
1
ρ
∂p
∂q
k
−
∂φ
∂q
k
+
∂
∂q
k
v
2
D
2
=−
1
ρ
∂p
∂q
*
k
−
∂φ
∂q
*
k
+
∂
∂q
*
k
v
2
D
2
−
1
√
g
kk
∂
∂t
W
k
D
=−
∂
∂t
W
k
D
√
g
kk
+ W
k
D
∂
∂t
1
√
g
kk
=−
∂
∂t
W
k
D
*
−
W
k
D
*
√
g
kk
∂
√
g
kk
∂t
−
2W
n
D
ω
nk
√
g
kk
=−
2W
n
D
ω
nk
√
g
kk
√
g
nn
√
g
nn
=−2W
n
D
*
ω
*
nk
(18.35)
Recall that k is not a summation index. Substituting the various terms of (18.35)
