Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


17.4 Derivation of the stability criteria in the geostrophic wind field 501
where ω refers to the natural frequency of the system. The four constants and the
trajectory are evaluated with the help of the following initial conditions:
t = 0: x = x
0
,u= u
g
(y = 0); y = y
0
= 0,v= v
0
=⇒
A = D = 0,B=
v
0
η
g
(0)
ω
=
v
0
ω
f
0
,C= v
0
(17.36)
where (17.20) and (17.35) have been utilized. In order to obtain the trajectory
we use (17.36) in (17.35) and integrate the resulting equation over time. After
introducing the moving coordinate system, as before, by means of
ξ = x − u
g
(0)t, ξ
0
= x(t = 0) = x
0
(17.37)
we find that the equation of the trajectory is given by
ξ −
ξ
0
+
v
0
η
g
(0)
2
+ y
2
f
0
η
g
(0)
=
v
2
0
η
g
(0)
2
since u
g
(y) ≈ u
g
(0) +
∂u
g
∂y
(0)y = u
g
(0) +
∂u
g
∂y
(0)
v
0
ω
sin(ωt)
(17.38)
For the trajectory of the air parcel in the moving system we distinguish three
cases:
η
g
(0)
>0 ellipse stable case
=f
0
> 0 circle stable case
<0 hyperbola unstable case
(17.39)
For the cases in which the displaced air parcels eventually return to their original
positions (circle, ellipse) we have the stable situation. In case of the hyperbola
the air parcel continues to be displaced from the original position, so we have the
unstable situation. For η
g
(0) = f
0
(17.38) reduces to (17.19). The special situation
η
g
(0) = 0 will be discussed in Problem 2.
17.4 Derivation of the stability criteria in the geostrophic wind field
Hydrostatic stability is a special stability case of atmospheric motion characteriz-
ing the vertical displacement of an air parcel. In contrast to this, inertial stability
concerns a purely horizontal displacement in case of an indifferent hydrostatic
equilibrium. Both effects taken together lead to consideration of the so-called
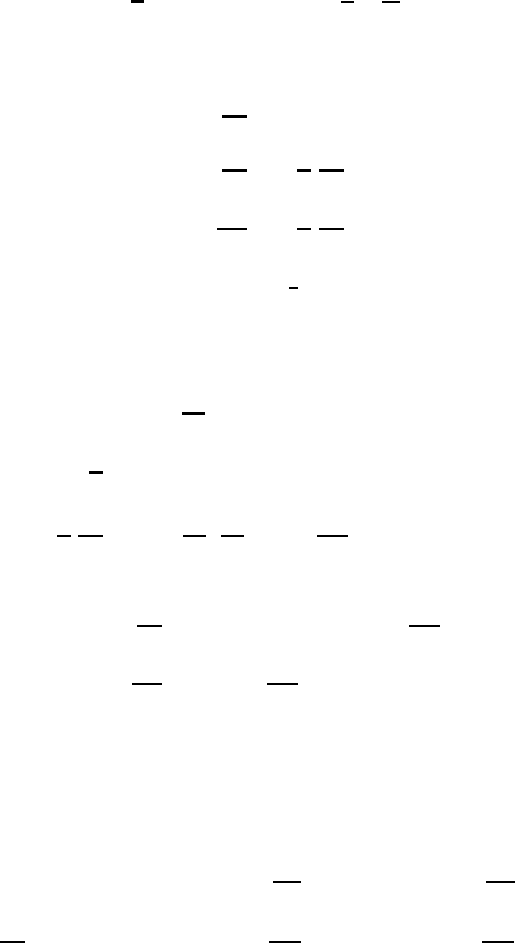
502 Inertial and dynamic stability
dynamic stability. The stability of the geostrophic wind field was first investigated
by Kleinschmidt (1941a and b) and was thoroughly discussed by Van Mieghem
(1951).
The fundamental assumption is the existence of a basic geostrophic shear wind
field,
u(y) = u
g
(y) = 0, v = w = 0(17.40)
On this basic field of motion with ∂p/∂x = 0 we superimpose an adiabatic
perturbation, which is assumed to obey the system of equations
(a)
dI
dt
= 0
(b)
dv
dt
=−
1
ρ
∂p
∂y
− f
0
u
(c)
dw
dt
=−
1
ρ
∂p
∂z
− g
(17.41)
with
I = u − f
0
(y − y
0
), I = I
g
= u
g
− f
0
(y − y
0
)(17.42)
where the overbar refers to the mean flow. It is customary to introduce the Exner
function as a variable instead of the pressure p by means of
(a) = c
p,0
p
p
0
k
0
,k
0
= R
0
/c
p,0
(b)
1
ρ
= θR
0
p
−k
0
0
p
k
0
−1
(c)
1
ρ
∂p
∂s
= c
p,0
θ
∂
∂s
p
p
0
k
0
= θ
∂
∂s
,s= x,y, z
(17.43)
Using (17.42) and (17.43c), equations (17.41b) and (17.41c) then read
dv
dt
=−f
0
I − f
2
0
(y − y
0
) − θ
∂
∂y
dw
dt
=−g − θ
∂
∂z
(17.44)
and represent the motion in the (y,z)-plane while equation (17.41a) remains
unaltered.
For ease of mathematical manipulation the two equations for the perturbed
motion in the (y,z)-plane will be symmetrized in order to represent the motion by
a vector. For this purpose we define two new functions by means of
L = f
0
(y − y
0
),
∂L
∂y
= f
0
,
∂L
∂z
= 0
H =
f
2
0
2
(y − y
0
)
2
+ g(z − z
0
),
∂H
∂y
= f
2
0
(y − y
0
),
∂H
∂z
= g
(17.45)

17.4 Derivation of the stability criteria in the geostrophic wind field 503
Using the definitions of the new functions, the equation of motion reads
dI
dt
= 0
dv
dt
=−I
∂L
∂y
−
∂H
∂y
− θ
∂
∂y
dw
dt
=−I
∂L
∂z
−
∂H
∂z
− θ
∂
∂z
(17.46)
Combination of the (y,z)-components of the perturbed motion gives
dv
v
dt
=−I ∇
v
L −∇
v
H − θ ∇
v
with v
v
= jv + kw, ∇
v
= j
∂
∂y
+ k
∂
∂z
(17.47)
The suffix v denotes the vertical (y,z)-plane. Introduction of the arbitrary displace-
ment s in the (y,z)-plane transforms (17.47) into
d
2
s
dt
2
=−I
∂L
∂s
−
∂H
∂s
− θ
∂
∂s
(17.48)
Assuming that we have parcel-dynamic conditions, not only ∂L/∂s and ∂H/∂s
but also ∂/∂s of the perturbed field are equivalent to the corresponding values
of the basic field. Therefore, due to the equilibrium conditions of the undisturbed
surroundings of the displaced particle in the (y,z)-plane, we have
0 =−
I
∂L
∂s
−
∂H
∂s
−
θ
∂
∂s
(17.49)
where I and θ refer to the basic field variables. Subtraction of (17.49) from (17.48)
eliminates ∂H/∂s, resulting in
d
2
s
dt
2
=−(I − I )
∂L
∂s
− (θ −
θ)
∂
∂s
(17.50)
We now assume that the perturbed motion takes place from y
0
= 0withinvariant
I and θ . At the original position the perturbed and the basic field quantities are
identical, so, due to the invariance of I and θ, we have at position s
I (s) =
I (0),θ(s) = θ(0) (17.51)
In contrast to this, we find for the basic field at position s
I (s) ≈ I (0) +
∂I
∂s
(0)s,
θ(s) ≈ θ (0) +
∂θ
∂s
(0)s (17.52)
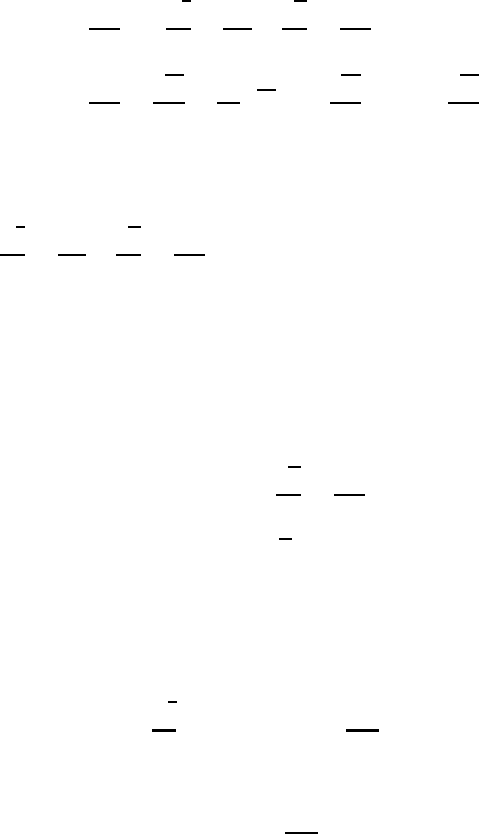
504 Inertial and dynamic stability
where we have discontinued the Taylor expansion after the linear term. All con-
sequences derived from the following equations are then valid only to within this
approximation. Using this information, equation (17.50) transforms into
d
2
s
dt
2
−
∂
I
∂s
(0)
∂L
∂s
+
∂
θ
∂s
(0)
∂
∂s
s = 0
with
∂
∂s
=
∂
∂s
=
∂
∂s
(0) +
∂
∂s
(0)s
=
∂
∂s
(0) = constant
(17.53)
describing the perturbed motion in the (y, z)-plane. This equation has the well-
known solution properties
∂
I
∂s
(0)
∂L
∂s
+
∂
θ
∂s
(0)
∂
∂s
<0 vibration solution dynamic stability
=0 transition the indifferent case
>0 exponential solution dynamic instability
(17.54)
We will briefly discuss two examples representing two important special cases.
Example 1: Static stability The displacement occurs in the vertical direction: s =
z − z
0
.Since∂L/∂z = 0, dynamic stability is obtained if
∂
θ
∂z
(0)
∂
∂z
< 0(17.55)
Since ∂/∂z < 0wemusthave∂θ/∂z(0) > 0, which is the well-known criterion
of hydrostatic stability.
Example 2: Inertial stability The displacement occurs in the horizontal direction y
along an isobaric surface, so (∂/∂y)
= 0. Now (17.54) yields dynamic stability
if
∂
I
∂y
(0)f
0
< 0or
∂u
g
∂y
(0) − f
0
f
0
< 0(17.56)
Since f
0
> 0 we have again the inertial-stability criterion (17.31):
∂u
g
∂y
(0) <f
0
(17.57)
17.5 Sectorial stability and instability
It is somewhat easier to treat the problem of sectorial stability and instability by
eliminating the Exner function in (17.54). We proceed by eliminating ∂/∂s by
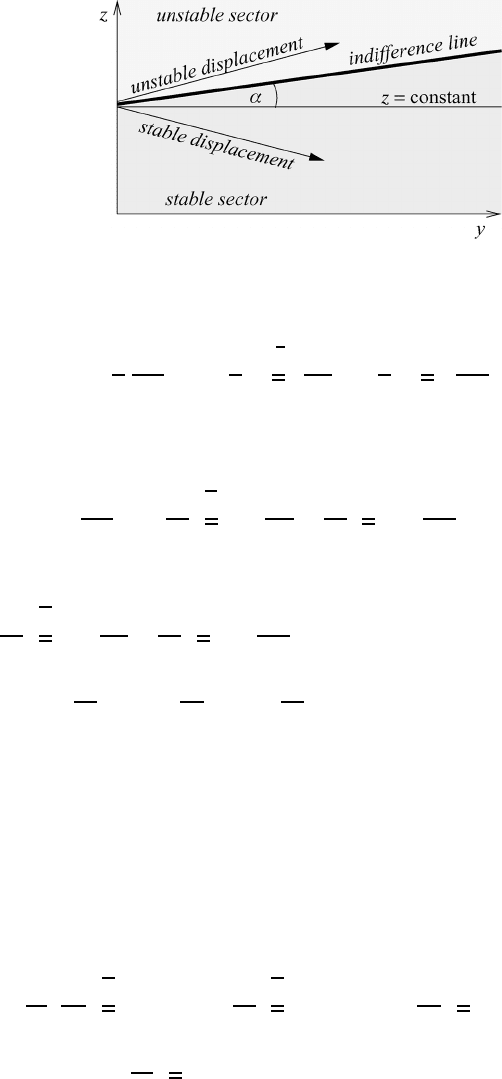
17.5 Sectorial stability and instability 505
Fig. 17.4 An indifference line separating stable and unstable sectors.
obvious steps from (17.48) and (17.49) and obtain
1
θ
d
2
s
dt
2
=−
I
θ
−
I
θ
∂L
∂s
−
1
θ
−
1
θ
∂H
∂s
(17.58)
Steps analogous to (17.51) and (17.52) with a slight additional approximation result
in the differential equation of the displacement in the form
d
2
s
dt
2
− θ
∂
∂s
I
θ
(0)
∂L
∂s
+
∂
∂s
1
θ
(0)
∂H
∂s
s = 0(17.59)
whose solution properties are given by
∂
∂s
I
θ
(0)
∂L
∂s
+
∂
∂s
1
θ
(0)
∂H
∂s
<0 dynamic stability
=0 the indifferent case
>0 dynamic instability
with
∂
∂s
= cos α
∂
∂y
+ sin α
∂
∂z
(17.60)
We have included in (17.60) a well-known transformation of the partial derivatives
relating the direction s to directions y and z by means of an angle α, which will be
defined now. It stands to reason that the regions of stability and instability in the
(y,z)-plane will be separated by a line of indifference; see Figure 17.4. We wish
to find the direction of this indifference line.
In this general display the regions of stability and instability could have been
interchanged. Application of the transformation listed in (17.60) together with
(17.45) to the condition of indifference at the point (y
0
= 0,z) yields
f
0
g
∂
∂y
I
θ
(0) + tan α
∂
∂z
I
θ
(0)
+ tan α
∂
∂y
1
θ
(0)
+ tan
2
α
∂
∂z
1
θ
(0) = 0
(17.61)

506 Inertial and dynamic stability
This relation is a quadratic equation for tan α, which defines at (y
0
= 0,z)the
inclination of the indifference line with respect to the y-axis. Therefore, there exist
two directions for the indifferent behavior of the displaced air parcel.
As the next step we find an expression for the inclination of an isentropic surface
with respect to the y-axis at y
0
= 0. This is easily done by using the differential
expression
d
1
θ
=
∂
∂z
1
θ
dz +
∂
∂y
1
θ
dy = 0(17.62)
from which it follows that
dz
dy
θ=constant
=−
∂
∂y
1
θ
∂
∂z
1
θ
= tan α
θ
= constant (17.63)
On dividing (17.61) by [∂(1/
θ)/∂z](0) we easily find
tan
2
α + tan α
−tan α
θ
+
f
0
g
∂
∂z
I
θ
(0)
∂
∂z
1
θ
(0)
+
f
0
g
∂
∂y
I
θ
(0)
∂
∂z
1
θ
(0)
= 0(17.64)
where use of equation (17.63) has been made. To finish our analysis we first return
to the equilibrium condition (17.49) which will be applied to the special directions
y and z, as is shown next:
(a) s = y:0=−
I
∂L
∂y
−
∂H
∂y
−
θ
∂
∂y
=−
If
0
− f
2
0
(y − y
0
) − θ
∂
∂y
(b) s = z:0=−
I
∂L
∂z
−
∂H
∂z
− θ
∂
∂z
=−g − θ
∂
∂z
(17.65)
On dividing both equations by θ and differentiating (17.65a) with respect to z and
(17.65b) with respect to y we obtain at y
0
= 0 the expressions
(a) 0 =−f
0
∂
∂z
I
θ
(0) −
∂
2
∂y ∂z
(0)
(b) 0 =−g
∂
∂y
1
θ
(0) −
∂
2
∂y ∂z
(0)
(17.66)
We eliminate the Exner function by subtraction and find
∂
∂z
I
θ
(0) =
g
f
0
∂
∂y
1
θ
(0) (17.67)

17.5 Sectorial stability and instability 507
By using this expression in the third term from the left in (17.64) we find with the
help of (17.63)
f
0
g
∂
∂z
I
θ
(0)
∂
∂z
1
θ
(0)
=
∂
∂y
1
θ
(0)
∂
∂z
1
θ
(0)
=−tan α
θ
(17.68)
and therefore
tan
2
α − 2tanα tan α
θ
+
f
0
g
∂
∂y
I
θ
(0)
∂
∂z
1
θ
(0)
= 0(17.69)
The solution of this quadratic equation is given by
tan α
1,2
= tan α
θ
±
tan
2
α
θ
−
f
0
g
∂
∂y
I
θ
(0)
∂
∂z
1
θ
(0)
(17.70)
The existence of two indifference lines in the (y, z)-plane requires that the
discriminant be greater than zero. If this is the case then the two indifference
lines are arranged as shown in Figure 17.5.
In order to investigate the indifference behavior, the discriminant in (17.70) will
be reformulated. This is best accomplished by introducing the potential tempera-
ture as the vertical coordinate. In (M4.51) it was shown that, for an arbitrary function
Fig. 17.5 The arrangement of two indifference lines.
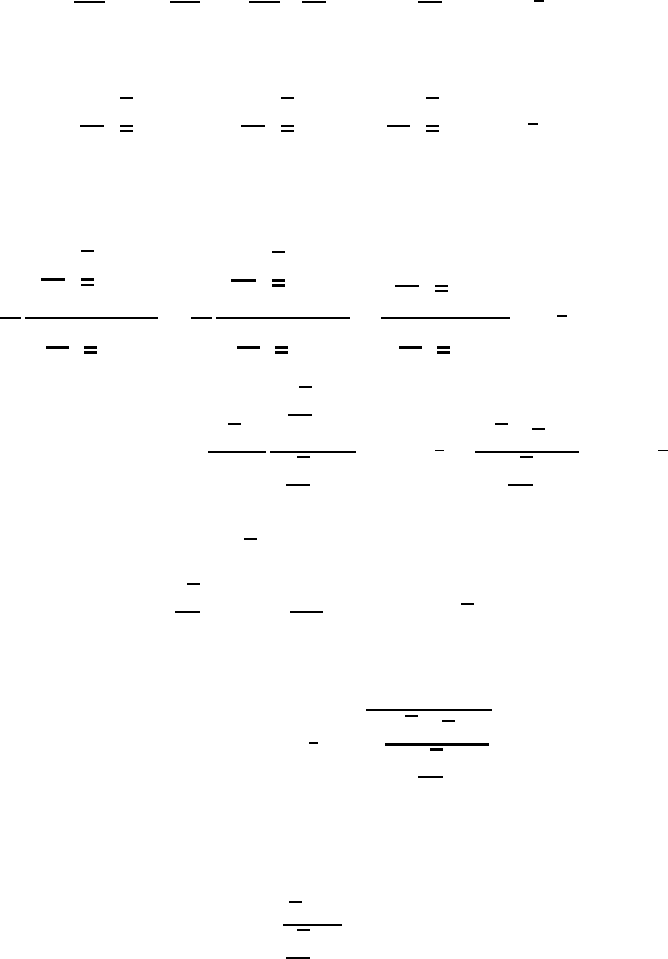
508 Inertial and dynamic stability
ψ, the following transformation relation is valid:
∂ψ
∂y
z
=
∂ψ
∂y
θ
−
∂ψ
∂z
∂z
∂y
θ
,
∂z
∂y
θ
= tan α
θ
(17.71)
Application of this formula at y
0
= 0gives
∂
∂y
I
θ
(0)
z
=
∂
∂y
I
θ
(0)
θ
−
∂
∂z
I
θ
(0) tan α
θ
(17.72)
Utilizing (17.72) together with (17.67) yields the second part of the discriminant
as
f
0
g
∂
∂y
I
θ
(0)
z
∂
∂z
1
θ
(0)
=
f
0
g
∂
∂y
I
θ
(0)
θ
∂
∂z
1
θ
(0)
−
∂
∂y
1
θ
(0)
z
∂
∂z
1
θ
(0)
tan α
θ
=−
f
0
θ(0)
g
∂
I
∂y
θ
(0)
∂θ
∂z
(0)
+ tan
2
α
θ
=
f
0
θ(0)η
θ
(0)
g
∂θ
∂z
(0)
+ tan
2
α
θ
(17.73)
In this expression the vorticity
η
θ
(0) has been introduced according to (17.42):
∂
I
∂y
θ
(0) =
∂u
g
∂y
θ
(0) − f
0
=−η
θ
(0) (17.74)
Instead of (17.70) we finally obtain
tan α
1,2
= tan α
θ
±
−
f
0
θ(0)η
θ
(0)
g
∂θ
∂z
(0)
(17.75)
which can be more easily interpreted. This equation reveals that the indifferent
behavior is possible only if the potential vorticity expression of the basic field at
y
0
= 0 is restricted by
η
θ
(0)
∂θ
∂z
(0)
< 0(17.76)
This condition is the requirement for the existence of partial or sectorial stability or
instability. Hence there always exist two displacement directions s
1
and s
2
defining

17.6 Sectorial stability for normal atmospheric conditions 509
the indifference lines separating stable and unstable regions for displacements in
the (y,z)-plane. If, in contrast to (17.76),
η
θ
(0)
∂θ
∂z
(0)
> 0(17.77)
then no indifference lines exist. Therefore, we have either total stability or total
instability. If this is the case at the point being considered, i.e. at y
0
= 0 of the basic
field, then, independently of the selected direction s of the virtual displacement in
the (y,z)-plane, we have total dynamic stability for all directions if
∂
θ
∂z
(0) > 0and
η
θ
(0) > 0(17.78)
and total dynamic instability for all directions if
∂
θ
∂z
(0) < 0and
η
θ
(0) < 0(17.79)
On the other hand, the validity of (17.76) results in the formation of four sectors
with alternating regions of stability and instability.
17.6 Sectorial stability for normal atmospheric conditions
In order to investigate the sectorial stability for normal atmospheric conditions we
assume that we have hydrostatic stability, which is characterized by
[∂
θ(0)/∂z] > 0. According to (17.76) we then must have η
θ
(0) < 0. We now
wish to find the stable and unstable sectors. Obviously stable and unstable sectors
are separated by lines of indifference. Now we consider the displacement of an
air parcel along a line
θ = constant and consider the stability equation (17.60).
In this particular situation the second term of (17.60) vanishes and we obtain the
relation
1
θ
∂
I
∂s
θ
(0)
∂L
∂s
<0 dynamic stability
=0 the indifferent case
>0 dynamic instability
(17.80)
Now we expand ∂/∂s as shown in (17.60) by using (17.45) and find
f
0
cos
2
α
θ
θ
∂
I
∂y
θ
(0)
<0 dynamic stability
=0 the indifferent case
>0 dynamic instability
(17.81)
Note that, according to (17.42),
I is independent of the vertical coordinate z.Using
(17.74) we may rewrite this formula and find the very useful expression
−
f
0
cos
2
α
θ
θ
η
θ
(0)
<0 dynamic stability
=0 the indifferent case
>0 dynamic instability
(17.82)
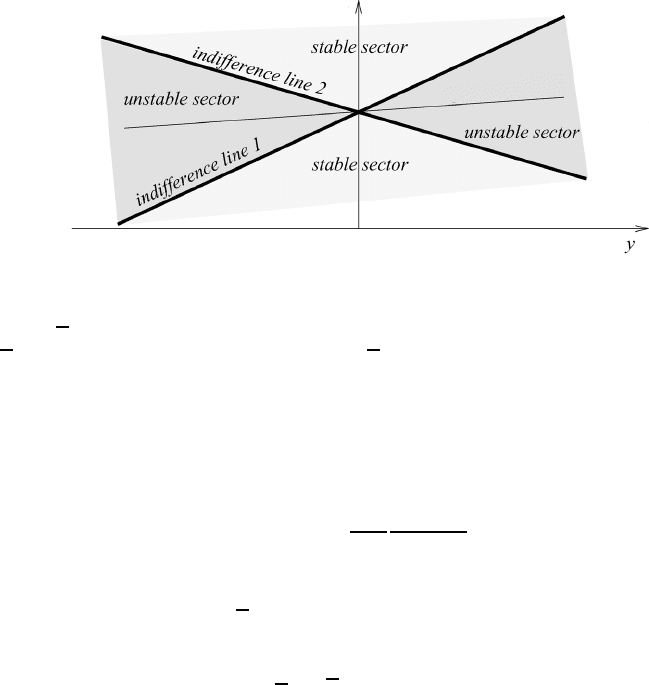
510 Inertial and dynamic stability
θ = constant = θ
᎑
z
Fig. 17.6 The arrangement of stable and unstable sectors for the normal atmosphere.
Since η
θ
(0) < 0 the lower unequality applies, so the displacement along the line
θ = constant is unstable. Thus, the line θ = constant is located in the unstable
sector as shown in Figure 17.6.
It is of some interest to determine the conditions which satisfy the requirement
η
θ
(0) < 0. We have previously given an expression relating the absolute vorticities
in the p and θ systems, see Section (10.4.5). This expression has the form
η
θ
= η
p
−
g
f
0
T
(∇
h,p
T )
2
γ
a
− γ
g
(17.83)
We recognize that the horizontal temperature gradient is mainly responsible for
satisfying the requirement
η
θ
(0) < 0. We will now estimate the limiting value for
the occurrence of sectorial stability. Assuming the validity of
η
p
= ζ
p
+ f
0
≈ f
0
(17.84)
we find for midlatitude situations, setting (17.83) equal to zero, that the limiting
value for the occurrence of sectorial stability is
|∇
h,p
T |≈2K/100 km (17.85)
Larger values of |∇
h,p
T | are common in frontal zones.
The reader interested in a more comprehensive discussion on dynamic stabil-
ity is referred to the detailed discussions presented by Van Mieghem (1951) in
the Compendium of Meteorology and in the textbook Dynamic Meteorology and
Weather Forecasting by Godske et al. (1957).
17.7 Sectorial stability and instability with permanent adaptation
In Section 17.4 we derived the equation for the perturbed motion (17.50) of an
air parcel. All results obtained so far followed from the invariance of I and the
