Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


22.3 The solution scheme using the pressure system 581
22.3.1 Initial data
At the starting time t
0
= 0 of the numerical integration we prescribe without any
restriction initial values of the prognostic variables p
s
and (v
1
,v
2
,θ)for0<
p<p
s
.
22.3.2 The diagnostic part
The hydrostatic equation and the continuity equation do not contain time deriva-
tives. Thus, they may be viewed as diagnostic relations or compatibility conditions.
With the help of the hydrostatic equation in the form
∂φ
∂p
=−
1
ρ
=−
R
0
T
p
=−
R
0
p
p
p
0
k
0
θ =−
R
0
p
k
0
0
θ
p
1−k
0
,k
0
=
R
0
c
p,0
(22.27)
we find a suitable expression for the geopotential, given by
φ(x,y, p) = φ
s
(x,y) +
R
0
p
k
0
0
p
s
p
θ
p
1−k
0
dp (22.28)
The suffix 0 refers to dry air. The continuity equation (22.20) permits the calculation
of the generalized vertical velocity, yielding
ω(x,y,p) =−m
2
0
p
0
∂v
1
∂x
+
∂v
2
∂y
dp (22.29)
In general, the integrals in (22.28) and (22.29) must be evaluated numerically.
22.3.3 The prognostic part
Let us assume that all required values of the variables φ and ω have been gener-
ated with the help of the initial data and the compatibility relations (22.28) and
(22.29). The local tendencies of v
1
,v
2
, and θ can be written down from (22.18) and
(22.25) by expanding the individual time derivative for each of these quantities.
The tendency of p
s
follows from (22.26). The complete set of prognostic equations
is summarized as
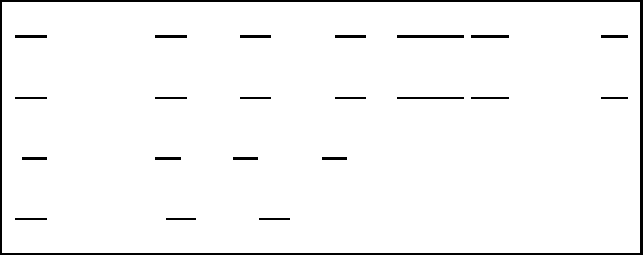
582 The stereographic system with a generalized vertical coordinate
∂v
1
∂t
=−m
2
0
v
1
∂v
1
∂x
+ v
2
∂v
1
∂y
− ω
∂v
1
∂p
−
v
2
1
+ v
2
2
2
∂m
2
0
∂x
+ fv
2
−
∂φ
∂x
∂v
2
∂t
=−m
2
0
v
1
∂v
2
∂x
+ v
2
∂v
2
∂y
− ω
∂v
2
∂p
−
v
2
1
+ v
2
2
2
∂m
2
0
∂y
− fv
1
−
∂φ
∂y
∂θ
∂t
=−m
2
0
v
1
∂θ
∂x
+ v
2
∂θ
∂y
− ω
∂θ
∂p
∂p
s
∂t
=−m
2
0
v
1,s
∂p
s
∂x
+ v
2,s
∂p
s
∂y
+ ω
s
(22.30)
The numerical integration is carried out by replacing the local time derivatives
by means of suitable finite-difference quotients. After the first time step (t,the
prognostic variables (v
1
,v
2
,θ,p
s
)areavailableatt
1
= t
0
+ (t.Theynowserve
as initial values for the next time step as well as for the new evaluation of the
diagnostic equations. This iteration must be continued until the entire prognostic
period has been covered.
The integration which we have described in principle is the integration scheme
which was used by Richardson (1922). However, he did not get any useful results
because he employed time steps that were too large. The maximum allowable time
step (t is specified by the so-called Courant–Friedrichs–Lewy criterion, which
will be explained later. When Richardson performed the numerical integrations
this criterion was still unknown.
22.4 The solution to a simplified prediction problem
In this section we are going to discuss the solution of the atmospheric system by
employing simplified boundary conditions. The method we are going to describe
has been applied successfully by Hinkelmann (1959) and his research group to
solve for the first time the atmospheric equations in their primitive (original) form.
The historical aspect by itself would not be sufficient to justify the discussion.
What is more important to us is to show that the simplifying assumptions often
cannot be restricted to a certain part of the system. Consequences resulting from
the simplifying assumptions must be carefully analyzed since they may influence
theentiresystem.
In the previous section we did not place any restriction on the lower bound-
ary surface p
s
(x,y, t). This oscillating lower boundary pressure surface generates
external gravity waves whose appearance may obscure the Rossby physics. More-
over, due to the high phase speed of the gravity waves, see Chapters 15 and 16,
the integration scheme requires very short time steps. In order to suppress these
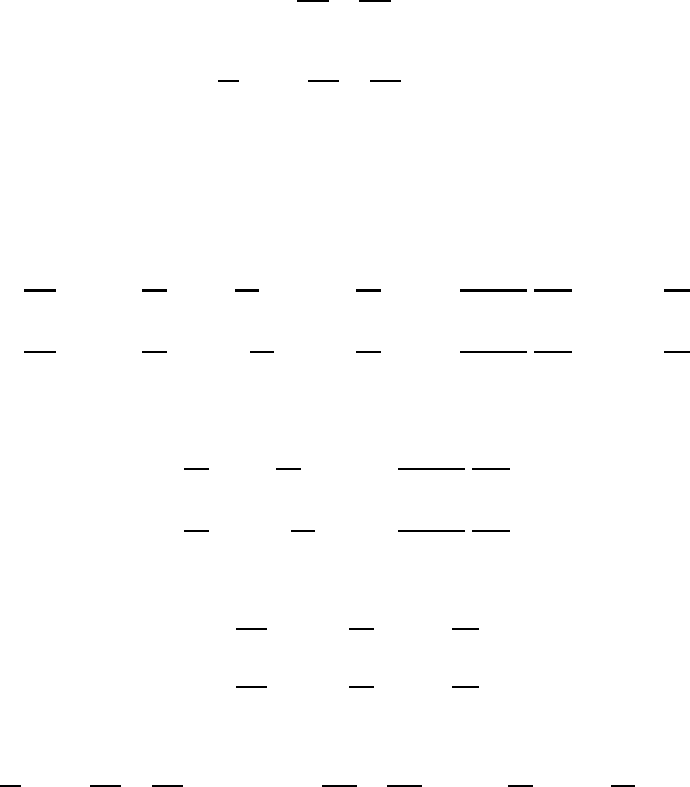
22.4 The solution to a simplified prediction problem 583
external gravity waves we assume that the lower pressure surface is fixed, say at
p
0
= 1000 hPa so that the generalized velocity ω now vanishes not only at the
upper but also at the lower boundary. An immediate consequence of this assump-
tion is that the horizontal velocities v
1
and v
2
at time t
0
= 0 cannot be prescribed
without any restrictions as before. By evaluating (22.29), which must be valid for
all times including t
0
= 0, we find the following unavoidable restriction on the
velocity components:
p
0
0
∂v
1
∂x
+
∂v
2
∂y
dp = 0(22.31)
so that
∂
∂t
p
0
0
∂v
1
∂x
+
∂v
2
∂y
dp
= 0(22.32)
Equation (22.32) provides a new boundary condition for the geopotential φ since
(22.28) is no longer valid due to the modified upper limit of the integral. In order to
enforce the condition (22.32) we must employ the equation of motion. We use the
stream-momentum formulation of the equation of motion in the p system, which
is easily obtained from (22.17) as
∂v
1
∂t
=−m
2
0
∂
∂x
v
2
1
+
∂
∂y
(v
1
v
2
)
−
∂
∂p
(v
1
ω) −
v
2
1
+ v
2
2
2
∂m
2
0
∂x
+ fv
2
−
∂φ
∂x
∂v
2
∂t
=−m
2
0
∂
∂x
(v
2
v
1
) +
∂
∂y
v
2
2
−
∂
∂p
(v
2
ω) −
v
2
1
+ v
2
2
2
∂m
2
0
∂y
− fv
1
−
∂φ
∂y
(22.33)
To simplify the notation, we introduce the following abbreviations:
F
1
=−m
2
0
∂
∂x
v
2
1
+
∂
∂y
(v
1
v
2
)
−
v
2
1
+ v
2
2
2
∂m
2
0
∂x
+ fv
2
F
2
=−m
2
0
∂
∂x
(v
2
v
1
) +
∂
∂y
v
2
2
−
v
2
1
+ v
2
2
2
∂m
2
0
∂y
− fv
1
(22.34)
Substituting (22.34) into (22.33) yields
∂v
1
∂t
= F
1
−
∂
∂p
(v
1
ω) −
∂φ
∂x
∂v
2
∂t
= F
2
−
∂
∂p
(v
2
ω) −
∂φ
∂y
(22.35)
so (22.32) can be written as
∂
∂t
p
0
0
∂v
1
∂x
+
∂v
2
∂y
dp
=
p
0
0
∂F
1
∂x
+
∂F
2
∂y
dp −
∂
∂x
(v
1
ω) +
∂
∂y
(v
2
ω)
p
0
0
−∇
2
h
p
0
0
φdp= 0
(22.36)

584 The stereographic system with a generalized vertical coordinate
The second term on the right-hand side is zero due to the vanishing of generalized
velocities ω at the lower and upper boundaries of the model.
Next we introduce the vertical mean of the geopotential,
φ =
1
p
0
p
0
0
φdp (22.37)
into (22.36) and obtain
∇
2
h
φ =
1
p
0
p
0
0
∂F
1
∂x
+
∂F
2
∂y
dp (22.38)
This Poisson-type equation is a balance equation for
φ. Let us assume that proper
boundary conditions have been stated for
φ and that (22.38) has been solved so
that φ(x,y) is a known quantity.
We will now integrate the hydrostatic equation (22.27) to find the geopotential
φ(x,y, p). Instead of (22.28) we now obtain
φ(x,y, p) = φ(x,y, p
0
) +
R
0
p
k
0
0
p
0
p
θ
p
1−k
0
dp (22.39)
where φ(x, y,p
0
) is still an unknown quantity for which we must find a suitable
expression. Integration of (22.37) by parts results in
φ(x, y) = φ(x,y,p
0
) −
1
p
0
p
0
0
p
∂φ
∂p
dp (22.40)
By elimination of φ(x,y,p
0
) between the latter two equations and also using
(22.27), we find
φ(x,y, p) =
φ(x, y) +
R
0
p
k
0
0
p
0
p
θ
p
1−k
0
dp −
p
0
0
p
k
0
θ
p
0
dp
(22.41)
which can be evaluated to give the geopotental at all required coordinates.
The prediction now follows the integration cycle of the previous section. The
tendencies of the quantities (v
1
,v
2
,θ) are taken from (22.30). The calculation of the
geopotential makes use of (22.41) thus guaranteeing that the boundary condition
(22.31) is satisfied.
22.5 The solution scheme with a normalized pressure coordinate
In this section we introduce the so-called σ system, which is defined by
ξ = p/p
s
= σ (22.42)
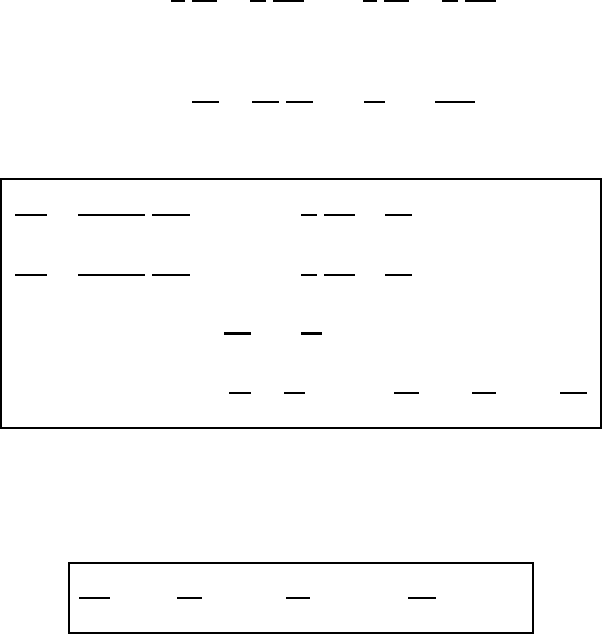
22.5 The solution scheme with a normalized pressure coordinate 585
This very useful coordinate transformation was introduced by Phillips (1957).
Since the vertical coordinate σ also decreases with height, the σ system is also
left-handed. The integration region is limited by σ = 0andσ = 1. Thus, the
mountainous orographic surface of the earth φ = φ
s
(x,y) coincides with the
surface of the constant vertical coordinate σ = 1wherep = p
s
.Atthelower
and at the upper boundary the generalized velocity ˙σ = 0. This statement results
from the application of the kinematic boundary condition requiring that the normal
component of the velocity must be zero at the boundaries. It is this simple form
of the lower boundary condition that provides the advantage of the σ system over
the p system. It should be clearly understood that ˙σ is not zero because the
derivative of a constant is zero. If this were the reason for ˙σ vanishing at the
boundaries, the generalized vertical velocity would be zero everywhere. This is, of
course, not the case.
According to (22.10) the pressure gradient and the geopotential gradient must be
evaluated along constant σ -surfaces. Therefore, the horizontal pressure gradients
may be written as
1
ρ
∂p
∂x
=
σ
ρ
∂p
s
∂x
,
1
ρ
∂p
∂y
=
σ
ρ
∂p
s
∂y
(22.43)
The hydrostatic equation is given by
∂φ
∂σ
=
∂φ
∂p
∂p
∂σ
=−
p
s
ρ
=−
R
0
T
σ
(22.44)
Therefore, the covariant equation of motion (22.10) assumes the form
dv
1
dt
+
v
2
1
+ v
2
2
2
∂m
2
0
∂x
− fv
2
=−
σ
ρ
∂p
s
∂x
−
∂φ
∂x
dv
2
dt
+
v
2
1
+ v
2
2
2
∂m
2
0
∂y
+ fv
1
=−
σ
ρ
∂p
s
∂y
−
∂φ
∂y
∂φ
∂σ
=−
p
s
ρ
with
d
dt
=
∂
∂t
+ m
2
0
v
1
∂
∂x
+ v
2
∂
∂y
+ ˙σ
∂
∂σ
(22.45)
Note that the horizontal gradients of the geopotential do not vanish since they
have to be evaluated along surfaces with σ = constant. The continuity equation
is obtained from (22.15) simply by replacing the generalized coordinate ξ by σ .
After expanding the individual derivative and rearranging terms we find
∂p
s
∂t
+ m
2
0
∂
∂x
(v
1
p
s
) +
∂
∂y
(v
2
p
s
)
+
∂
∂σ
(˙σp
s
) = 0 (22.46)

586 The stereographic system with a generalized vertical coordinate
Owing to the validity of the hydrostatic equation for all times, the atmospheric
fields φ and the unreduced surface pressure p
s
uniquely determine the atmospheric
mass field. We will now discuss the principle of the integration scheme.
22.5.1 Initial data
The geopotential of the earth’s surface φ
s
= (x,y) and the map factor m
0
(x,y)are
considered known. Moreover, the Coriolis parameter f appears in the prognostic
system. Since the latitude ϕ does not enter explicitly, we must express the sin ϕ
function by means of (20.29) so that the Coriolis parameter may be written as
f = f (x, y). The three quantities φ
s
,m
0
,andf do not depend on time. For the
initial time t
0
= 0, without any restriction, we prescribe the prognostic variables
p
s
at σ = 1and(v
1
,v
2
,θ)for0≤ σ ≤ 1.
22.5.2 The diagnostic part
By using the ideal-gas law and the potential-temperature formula, the hydrostatic
equation of the σ system can be rewritten as
∂φ
∂σ
=−
R
0
T
σ
=−R
0
p
s
p
0
k
0
σ
k
0
−1
θ (22.47)
Integration between the limits σ and 1 gives the geopotential
φ(x,y, σ) = φ
s
(x,y) + R
0
p
s
p
0
k
0
1
σ
(σ
)
k
0
−1
θdσ
(22.48)
Our next task is to find a suitable expression for the generalized vertical
velocity ˙σ . Integrating the continuity equation (22.46) between the limits σ = 0
and σ = 1gives
∂p
s
∂t
+ m
2
0
∂
∂x
1
0
v
1
p
s
dσ
+ m
2
0
∂
∂y
1
0
v
2
p
s
dσ
= 0(22.49)
since ˙σ vanishes at the boundaries of the model. We now eliminate the surface pres-
sure tendency ∂p
s
/∂t between (22.46) and (22.49) and then integrate the resulting
equation between σ = 0andσ . Recognizing that equation (22.49) is independent
of σ ,wefind
˙σ =−
m
2
0
p
s
σ
0
∂
∂x
(v
1
p
s
) +
∂
∂y
(v
2
p
s
)
dσ +
m
2
0
σ
p
s
1
0
∂
∂x
(v
1
p
s
) +
∂
∂y
(v
2
p
s
)
dσ
(22.50)
Since (v
1
,v
2
,θ,p
s
) are known at t
0
, we may proceed with the numerical integration
of (22.48) and of (22.50). Inspection of this equation shows that the condition ˙σ = 0
is satisfied at the lower and upper boundaries.
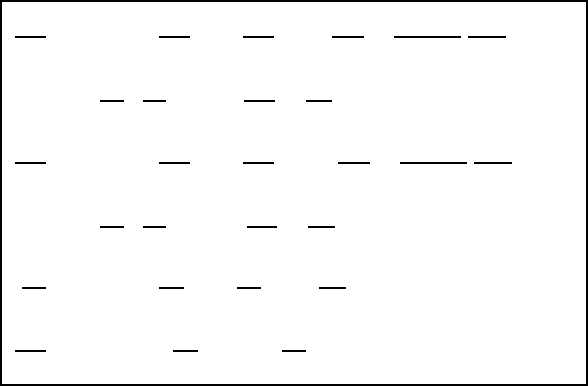
22.6 The solution scheme with potential temperature as vertical coordinate 587
22.5.3 The prognostic part
Using (22.49) and eliminating the density of the air, the prognostic set is given by
∂v
1
∂t
=−m
2
0
v
1
∂v
1
∂x
+ v
2
∂v
1
∂y
−˙σ
∂v
1
∂σ
−
v
2
1
+ v
2
2
2
∂m
2
0
∂x
+ fv
2
−
R
0
p
s
p
s
p
0
k
0
σ
k
0
θ
∂p
s
∂x
−
∂φ
∂x
∂v
2
∂t
=−m
2
0
v
1
∂v
2
∂x
+ v
2
∂v
2
∂y
− ˙σ
∂v
2
∂σ
−
v
2
1
+ v
2
2
2
∂m
2
0
∂y
− fv
1
−
R
0
p
s
p
s
p
0
k
0
σ
k
0
θ
∂p
s
∂y
−
∂φ
∂y
∂θ
∂t
=−m
2
0
v
1
∂θ
∂x
+ v
2
∂θ
∂y
−˙σ
∂θ
∂σ
∂p
s
∂t
=−m
2
0
1
0
∂
∂x
(v
1
p
s
) +
∂
∂y
(v
2
p
s
)
dσ
(22.51)
The partial derivatives may now be replaced by suitable finite-difference formulas
and the iteration of this system may be started. Knowing (v
1
,v
2
,θ,p
s
) after the first
iteration step, new values of the diagnostic quantities φ and ˙σ can be determined
by means of (22.48) and (22.50). The iterations may be carried out in the same
manner as we have described for the p system.
Finally, we wish to remark that, so far, all tendencies appeared explicitly. By this
we mean that they are not embedded in differential operators. A consequence is that
an increasing resolution of the grid results only in a linear growth of the numerical
work. This is not the case in some other numerical schemes. The integration
principle we have described in this section was used for a considerable period of
time by the Weather Services of the USA and Germany.
22.6 The solution scheme with potential temperature as vertical coordinate
By selecting the potential temperature as the generalized vertical coordinate, often
called the isentropic vertical coordinate, we require that the potential temperature
is a monotonically increasing function. This requirement reflects the observed
large-scale conditions. Thus, we may write
ξ = θ,
˙
ξ =
˙
θ (22.52)
If the atmosphere were adiabatically stratified in a certain height interval, there
could be no unique attachment of a potential temperature to height coordinates.

588 The stereographic system with a generalized vertical coordinate
Using the potential-temperature formula, we find that the components of the
pressure gradients along isentropic surfaces are given by
−
1
ρ
∂p
∂x
=−c
p,0
∂T
∂x
, −
1
ρ
∂p
∂y
=−c
p,0
∂T
∂y
(22.53)
By introducing the so-called Montgomery potential,
M = c
p,0
T + φ (22.54)
we may write for the right-hand sides of the horizontal equations of motion
−
1
ρ
∂p
∂x
−
∂φ
∂x
=−
∂M
∂x
, −
1
ρ
∂p
∂y
−
∂φ
∂x
=−
∂M
∂y
(22.55)
According to (22.9) the hydrostatic equation for the θ system is given by
−
1
ρ
∂p
∂θ
−
∂φ
∂θ
= c
p,0
T
θ
− c
p,0
∂T
∂θ
−
∂φ
∂θ
= 0(22.56)
Introduction of the Montgomery potential leads to the final form of the hydrostatic
equation:
∂M
∂θ
= c
p,0
T
θ
(22.57)
An attractive feature of the θ system is that, for dry adiabatic motion, the potential
temperature of each air parcel is conserved, so dθ/dt =
˙
θ = 0. The predictive set
(22.10) can then be written as
∂v
1
∂t
=−m
2
0
v
1
∂v
1
∂x
+ v
2
∂v
1
∂y
−
v
2
1
+ v
2
2
2
∂m
2
0
∂x
+ fv
2
−
∂M
∂x
∂v
2
∂t
=−m
2
0
v
1
∂v
2
∂x
+ v
2
∂v
2
∂y
−
v
2
1
+ v
2
2
2
∂m
2
0
∂y
− fv
1
−
∂M
∂y
∂
∂t
∂p
∂θ
=−m
2
0
∂
∂x
v
1
∂p
∂θ
+
∂
∂y
v
2
∂p
∂θ
(22.58)
The last expression is the continuity equation of the θ system.
The lower boundary condition on θ may be written as
dθ
s
dt
=
∂θ
s
∂t
+ m
2
0
v
1,s
∂θ
s
∂x
+ v
2,s
∂θ
s
∂y
= 0(22.59)
With increasing height the potential temperature increases to infinity while the
pressure and density decrease to zero. By utilizing (22.56) the upper boundary
condition may be written as
lim
θ→∞
ρ→0
∂p
∂θ
= c
p,0
lim
θ→∞
ρ→0
ρ
∂T
∂θ
−
ρT
θ
= 0(22.60)
where ∂T/∂θ is finite.

22.7 Problems 589
In order to find the pressure tendency we integrate the continuity equation, i.e.
the last equation of (22.58), between θ and θ →∞and obtain with the help of the
Leibniz rule
∂p
∂t
= m
2
0
∂
∂x
∞
θ
v
1
∂p
∂θ
dθ
+
∂
∂y
∞
θ
v
2
∂p
∂θ
dθ
(22.61)
For adiabatic flow the θ system has the decisive advantage that the vertical
velocity vanishes everywhere so that we are dealing with two-dimensional motion.
As soon as nonadiabatic effects must be taken into account this advantage is lost,
so the θ system is not used for routine numerical investigations. Therefore, we will
omit a detailed discussion of the integration cycle.
Finally, we would like to remark that other generalized vertical coordinates might
be used, such as the density of the air. The theory for this system has been worked
out, but it has not yet found many important applications.
22.7 Problems
22.1: By a direct transformation obtain the first equation of (22.11) from the first
equation of (22.10). Compare your result with equation (20.48).
22.2: Show that equations (22.20) and (22.21) follow from (22.15) and (22.16).
22.3: Balloons drifting on surfaces of constant density could be used to collect
global atmospheric data. To utilize these data, we need a predictive system using
ρ as a vertical coordinate.
(a) Introduce the Montgomery potential for the ρ system N = R
0
T + φ to find
the horizontal equation of motion in terms of the covariant velocity components.
Obtain the hydrostatic equation. State the individual derivative d/dt for this system.
(b) Find the continuity equation.
(c) Formulate the upper and lower boundary conditions for the ρ system.
(d) Find an expression for the pressure tendency ∂p/∂t.
22.4: Consider an idealized atmosphere consisting of an incompressible friction-
less fluid with a free surface z
H
. Assuming that v
h
is independent of height, find a
prognostic equation for the free surface.
22.5: Consider the equation of motion for a frictionless fluid in Cartesian coordi-
nates (m
0
= 1) in simplified form, i.e.
dv
h
dt
q
i
=−
1
ρ
∇
h,ξ
p − f k × v
h
−∇
h,ξ
φ

590 The stereographic system with a generalized vertical coordinate
where ∇
h,ξ
is the horizontal nabla operator in the arbitrary ξ system. Show that, for
the σ system, we may write the equation of motion in the form
∂
∂t
(.v
h
)
q
i
+∇
h,σ
·(.v
h
v
h
) +
∂
∂σ
(.v
h
˙σ )
=−∇
h,σ
(.φ) +
∂
∂σ
(φσ) ∇
h,σ
. − .f k × v
h
where σ = p/p
s
and . = p
s
/p
0
.
22.6: With the help of the Leibniz rule, verify equation (22.61).
22.7: Verify equation (22.46).
