Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

14.11 Nonlinear waves in the atmosphere 431

each layer are the same but the basic air currents differ, i.e. u

0,1

= u

0,2

,ρ

0,1

= ρ

0,2

the wave is always unstable because the dynamic term is always imaginary. These

waves are called shearing waves since the wave velocity depends only on the wind

shear.

Finally, we consider the stationary wave by setting the phase speed c equal to

zero. Furthermore, we assume that we are dealing with deep-water waves, L

 H .

In this special case the wavelength L

is expressed by

2π

0,1

+ ρ

0,2

− ρ

0,1

(14.146)

Using the ideal-gas law and recalling that, at the interface, the dynamic boundary

condition must hold (p

= p

= p), we ﬁnd the wavelength of the so-called billow

clouds to be

2π

0,1

+ u

0,2

− T

(14.147)

These clouds are observed to form at the boundary of an inversion. Assuming

that the clouds move with the mean velocity (u

0,1

+ u

0,2

)/2ofthelowerandthe

upper layer, the wave velocity vanishes in a coordinate system moving with the

velocity of the cloud system. Condensation and cloud formation take place when

the air is ascending while the sky is clear where the wave motion causes descent of

air. Comparison with observations shows that this simple theory overestimates the

wavelengths of the billow clouds. As early as 1931 Haurwitz improved the above

theory by permitting a variation in density of both air masses. This resulted in a

better agreement between theory and observations. If the difference in temperature

at the top of the inversion is about 4 K and the corresponding change in the wind

velocity 5.5 m s

−1

, the wavelength of the billow cloud is about 600 m. In this case

the above theory agrees reasonably well with observations.

14.11 Nonlinear waves in the atmosphere

There are other types of wave motion that cannot be handled using the methods

described so far. Instead of linear equations, nonlinear equations must be solved,

with their accompanying complexities. In this section we merely wish to make a

few comments on solitary waves, which are described by the so-called Korteweg–

de Vries equation. A quite informative mathematical introduction to this topic

is to be found, for example, in Keener (1988). Here we follow the introduction

given by Panchev (1985), who treats some aspects of meteorological applications

in connection with solitary waves.

A solitary wave is a localized perturbation propagating in a dispersive medium

without change of shape. If solitary waves collide without changing shape they

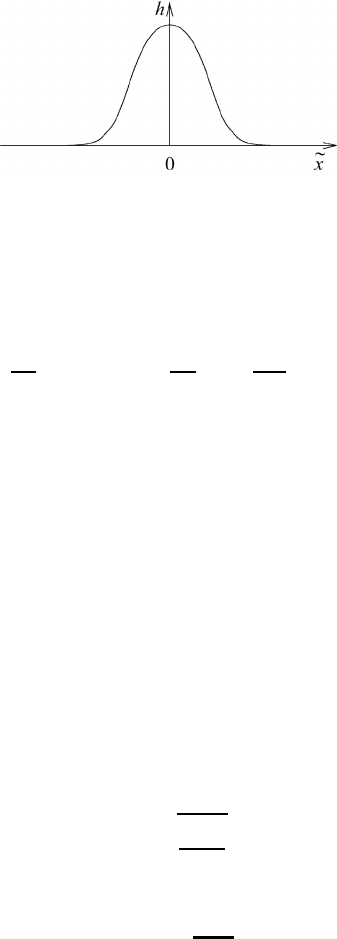
432 Wave motion in the atmosphere

Fig. 14.6 The shape of the solitary wave.

are called solitons. The Korteweg–de Vries equation, in the shallow-water

approximation, describes the evolution of long surface gravity waves with small

amplitudes. In the one-dimensional case this equation may be written as

∂h

∂t

+ (C

+ C

∂h

∂x

+ C

∂

∂x

= 0(14.148)

Here C

,andC

are constants and h(x,t) is the deviation from the free surface.

In the linear approximation (C

= 0) there exists the solution

h(x,t) = A exp[i(k

x − ωt)] with ω = C

− C

(14.149)

where A is the amplitude of the disturbance. The dispersion relation shows that the

angular frequency ω depends on the wavenumber k

only, not on the amplitude.

In the general case equation (14.148) also has a periodic solution that can be

expressed in terms of elliptic cosine functions (Jacobi’s elliptical function). It is

quite remarkable that, in addition to the periodic solution, equation (14.148) has a

particular solution that can be expressed in terms of the hyperbolic secant function

h(x,t) = A sech





(x − ct)



(14.150)

with





12C

and

c = C

The angular frequency depends not only on the wavenumber, as in the linear

case, but also on the amplitude. This is the most important property of dispersive

nonlinear waves.

Figure 14.6 shows the shape of the function h(˜x), that is the real part of h(˜x),

where ˜x = k

(x − ct). In the extremely far wings h approaches the value zero; at

14.11 Nonlinear waves in the atmosphere 433

Fig. 14.7 Interaction of two solitons.

the center of the disturbance h = A. A disturbance, i.e. the solitary wave, moves

in the positive x-direction with a speed c that is proportional to the amplitude A.

Linear equations do not behave in this way. From mathematical theory we know

that the superposition of solutions of linear systems gives another solution. Owing

to this fact, a neutral (not decaying or amplifying) linear wave can overtake another

neutral linear wave without the shape of either wave changing. In contrast to this,

the superposition of solutions of nonlinear equations does not give a new solu-

tion. Nevertheless, many solitary waves exhibit aspects of linear behavior. When

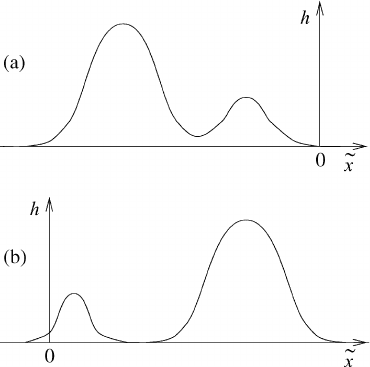
one solitary wave overtakes another, they interact nonlinearly. After separating

they retain their original shapes as shown in Figure 14.7. The soliton with the

larger amplitude overtakes a soliton of smaller amplitude as shown in part (b) of

Figure 14.7. The occurrence of nonlinearity follows from the observation that, after

the interaction, the solitons are not located at those coordinates where they would

have been found had no interaction taken place.

Finally, we brieﬂy describe a meteorological application. From a careful

analysis of the surface pressure ﬁeld, sometime in 1951 in Kansas, USA, a pressure

disturbance of 3.4 hPa was observed to propagate with a speed of about 21 m s

−1

to a distance of 800 km. Abdullah (1955) explains this phenomenon as an internal

gravitational solitary wave resulting from an impulsive motion of a quasi-stationary

cold front in the thermal inversion layer. Further observations of this type have been

presented by Christie et al. (1978).

434 Wave motion in the atmosphere

14.12 Problems

14.1: Sketch the proﬁle of the wave U = U

sin(kx − ωt + ) with  = π.

14.2: A standing or stationary wave can be described as the product U = U

(x)U

(t).

Show that the superposition of two waves of the same amplitude and the same pe-

riod moving in opposite directions can be written in this way. Assume that we are

dealing with simple sine waves and give the explicit form of U .

14.3: Let α

= constant,p

= constant, and u

= constant. Eliminate α



(14.31) and verify that pure sound waves move according to (14.37d). Assume that

δ = 1.

14.4: Let δ = 1,u

= 0, and g = 0 in the system (14.31). Introduce the transfor-

mation (14.82). Instead of α

= constant assume that the relative change in height

(1/α

) ∂α

/∂z is constant. Does this result in the phase speed of a pure sound

wave?

14.5: Show that the system of Lamb waves (14.79) satisﬁes the basic linearized

system (14.31). For simpliﬁcation set u

= 0.

14.6: Modify equation (14.142) for the case in which both ﬂuids are inﬁnitely

deep.

14.7: In shallow water the phase speed is given by (14.113) if the earth’s rotation is

ignored. Estimate the effect of the earth’s rotation. In this case c =



gH + f

if u

= 0.

14.8: Find an approximate wavelength of a lee wave forming behind a symmetric

mountain in a stable atmosphere. This wavelength is fairly well approximated by

a standing wave produced by vertical oscillations in a homogeneous current at a

height twice the height of the mountain. Assume that u

= 10 m s

−1

, the observed

lapse rate is −10 K km

−1

,andT

(3000 m) is 240 K.

14.9: Show that ω

= (g/α

) ∂α

/∂z − g

The barotropic model

Barotropic and baroclinic atmospheric processes manifest themselves in the numer-

ous facets of large-scale weather phenomena. Typical examples are the formation

and propagation of synoptic waves having wavelengths of several thousand kilo-

meters and the characteristic life cycles of high- and low-pressure systems. The

barotropic and baroclinic physics provides the physical basis of numerical weather

prediction. In this chapter we will consider various aspects of barotropic models. It

is realized that the prediction of the daily weather by means of barotropic models is

no longer practiced by the national weather services. Nevertheless, by discussing

the mathematical theory of the barotropic physics we can learn very well how phys-

ical variables are interconnected and how much care must be taken to construct even

a very simple prediction model. The ﬁrst numerical barotropic weather-prediction

model was introduced by the renowned meteorologist C. G. Rossby and by the

famous mathematician John von Neumann. Baroclinic models will be described in

some detail in later chapters.

Barotropic models are short-range-prediction models that include only the re-

versible part of atmospheric physics. The consequence is that the atmosphere is

treated as a one-component gas consisting of dry air. The irreversible physics such

as non-adiabatic heating and cloud formation is not taken into account.

15.1 The basic assumptions of the barotropic model

The name of the model is derived from the assumption that the atmosphere is in

a barotropic state throughout the prediction period. The condition of barotropy

by itself, however, is not sufﬁcient to construct a barotropic prediction model;

additional assumptions are mandatory. The model described here rests on three

basic assumptions. These are

435

436 The barotropic model

(i) the validity of the condition of barotropy for the entire prediction period:

ρ = ρ(p)or∇ρ ×∇p = 0fort ≥ t

(15.1)

(this is known as the condition of autobarotropy)

(ii) the validity of the hydrostatic equation at all times

∂p

∂z

=−gρ for t ≥ t

(15.2)

(iii) the horizontal wind is independent of height

∂v

∂z

= 0fort ≥ t

(15.3)

The assumption of hydrostatic equilibrium is also an integral part of most baro-

clinic large-scale-weather-prediction models. It can be shown that conditions (i)

and (ii) imply that the horizontal pressure-gradient force is independent of height.

This is equivalent to stating that the geostrophic wind is height-independent or that

the thermal wind vanishes. In contrast to this, the strength of the thermal wind is a

measure of atmospheric developments in baroclinic models. Moreover, the hydro-

static assumption implies the removal of the rapidly moving vertical sound waves.

This is important since the ﬁltering of the rapidly moving “noise” waves permits

a larger time step in the numerical integration of the model equations. Insofar as

condition (iii) is concerned, it may be replaced by a weaker statement. Indeed, it is

sufﬁcient to require that the horizontal wind is height-independent at the beginning

of the prediction period since (i) and (ii) automatically guarantee that the horizontal

wind remains height-independent at all later times. We will prove this statement at

the end of Section 15.2.1.

There also exists the so-called equivalent barotropic model, in which the actual

horizontal wind changes with height in a prescribed manner. We are not going to

discuss this type of model since it requires various empirical modiﬁcations that are

not entirely consistent with the remaining physics of the model.

A few remarks on the assumptions involved in the model may be helpful. As-

sumption (i) does not permit the formation of isobaric temperature gradients. All

development processes are thermally inactive. Thus we ignore the ﬁrst and second

laws of thermodynamics. Only one thermodynamic variable, either pressure or

density, needs to be controlled.

Assumption (ii), as we have demonstrated in the previous chapter, eliminates

vertically propagating sound waves. If the wavelength of the disturbance becomes

comparable to the depth of the homogeneous atmosphere, the hydrostatic assump-

tion becomes unrealistic.

15.2 The unﬁltered barotropic prediction model 437

Assumption (iii) together with assumptions (i) and (ii) reduces the model at-

mosphere to a spatially two-dimensional system. In contrast to this, all baroclinic

models are three-dimensional, thus simulating atmospheric processes more real-

istically. Hence, the barotropic model applies to one pressure level only, which

is usually taken as the 500-hPa surface. There the model physics applies best.

Owing to the special assumptions of the model the barotropic model suppresses

the synoptically relevant interactions of height-dependent velocity divergences and

temperature varations which are responsible for the transformation of potential

energy into kinetic energy on a signiﬁcant scale. Development processes such as

frontogenesis and occlusions are suppressed by the barotropic model. At most,

transformations between the kinetic energy of the mean ﬂow and the disturbances

are taking place.

Finally, it should be realized that there are numerous variants of the barotropic

model. We are going to discuss unﬁltered and ﬁltered barotropic models, in which

the gravitational surface waves are eliminated by means of diagnostic relations.

From the historical point of view it is interesting to remark that

the

ﬁrst barotropic

model using actual meteorological data was successfully applied by Charney and

Eliassen (1949). They used a ﬁltered linearized version of the model.

15.2 The unﬁltered barotropic prediction model

15.2.1 The general barotropic model

We will now consider the barotropic model without the elimination of the rapidly

moving surface gravity waves. The elimination of these fast waves is called noise

ﬁltering. Let us consider a large enough section of the atmosphere so that the

hydrostatic equation applies. For simplicity, we represent the ﬁeld of motion on

a tangential plane ﬁxed to the earth where the motion is described in terms of

Cartesian coordinates. The surface of the earth is the rigid lower boundary z

(x,y)

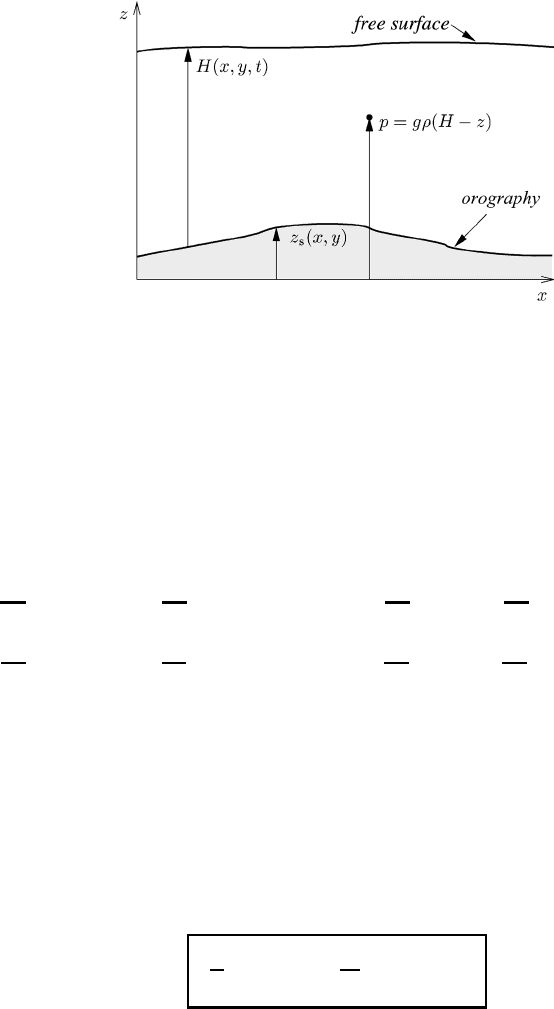
while the upper boundary is assumed to be a free surface, H (x, y,t). The pressure

at the earth’s surface will be denoted by p

(x,y, t); the hydrostatic pressure at the

free surface vanishes as depicted in Figure 15.1.

At an arbitrary reference level z the hydrostatic pressure is given by

p(x,y, z,t) = g



ρdz



(15.4a)

so that the surface pressure may be written as

(x,y, t) = p(x,y, z,t) + g



ρdz



(15.4b)

438 The barotropic model

Fig. 15.1 A vertical cross-section of the atmosphere in the (x,z)-plane.

Since the horizontal pressure gradient force is height-independent we may compute

this gradient everywhere, including at the earth’s surface. We must keep in mind,

however, that the occurrence of orography will modify the surface pressure gradient.

In order to handle this situation we apply the Leibniz rule to (15.4b). We ﬁrst

carry out the partial differentiations with respect to the horizontal coordinates.

Remembering that z

also depends on x and y, we obtain

∂

∂x

(x,y, t)] =

∂

∂x

[p(x,y, z,t)] + g



∂ρ

∂x



− gρ

∂

∂x

(x,y)]

∂

∂y

(x,y, t)] =

∂

∂y

[p(x,y, z,t)] + g



∂ρ

∂y



− gρ

∂

∂y

(x,y)]

(15.5a)

with ρ

= ρ(p(z

),t). Combining these equations leads to

∇

p(x,y, z,t) =∇

− g



∇

ρdz



+ gρ

∇

(15.5b)

On letting z approach z

the integral will vanish. Thus, in the limit z −→ z

ﬁnd



∇



z=z

∇

+∇

(15.6)

Here we have introduced the geopotential φ

(x,y) of the earth’s surface, which is

a time-independent quantity and may be computed with the help of a suitable map,

i.e. φ

(x,y) = gz

(x,y).

15.2 The unﬁltered barotropic prediction model 439

Since in the barotropic model the horizontal pressure gradient is independent of

height, we may introduce (15.6) into (2.29) to obtain the equation of motion for

frictionless ﬂow on the tangential plane as



∂v

∂t





+ v

·∇

+ f i

× v

∇

+∇

= 0

(15.7)

Recall that the vertical line attached to the local time derivative simply means

that the basis vectors are not to be differentiated with respect to time. Their time

dependency is already contained in the Coriolis term. As usual, the sum of the local

acceleration term and the advection term can be combined to give the horizontal

acceleration. To complete the prognostic system we must involve the continuity

equation

∂ρ

∂t

+∇

· (ρv

) +

∂

∂z

(ρw) = 0(15.8)

In order to apply the kinematic boundary conditions, this equation will be integrated

from the lower to the upper boundary of the atmosphere, yielding



∂ρ

∂t

dz +



∇

· (ρv

) dz + (ρw)



= 0(15.9)

Reference to equations (9.43b) and (9.43c) shows that these boundary conditions

may be written as

w(H ) =

∂H

∂t

+ v

·∇

H, w(z

) = v

·∇

(15.10)

The ﬁrst term of (15.9) will now be given a more suitable form with the help of the

Leibniz rule

∂

∂t



ρdz=



∂ρ

∂t

dz + ρ

∂H

∂t

(15.11)

with ρ

= ρ(p(H ),t). The second term in (15.9) will also be rewritten with the

help of the Leibniz rule. The differentiation with respect to the coordinate x yields

∂

∂x



ρu dz =



∂

∂x

(ρu) dz + (ρu)



∂H

∂x

− (ρu)



∂z

∂x

(15.12)

The differentiation with respect to y is accomplished by simply replacing x by the

coordinate y. Therefore, the second term of (15.12) can be written as



∇

· (ρv

) dz =∇



(ρv

) dz − (ρu)



∂H

∂x

+ (ρu)



∂z

∂x

− (ρv)



∂H

∂y

+ (ρv)



∂z

∂y

(15.13)

440 The barotropic model

Substituting (15.10), (15.11), and (15.13) into (15.9) gives

∂

∂t



ρdz− ρ

∂H

∂t

+∇



ρv

dz − ρ

·∇

+ ρ

·∇

+ ρ



∂H

∂t

+ v

·∇



− ρ

·∇

= 0

(15.14)

in which several terms cancel out. Finally we obtain

∂

∂t



ρdz+∇



ρv

dz = 0(15.15)

On multiplying both sides of (15.15) by the acceleration due to gravity g and

recalling that the horizontal velocity is height-independent, we ﬁnd in view of

(15.4a) the surface-pressure tendency equation

∂p

∂t

+∇

· (v

) = 0

(15.16)

For the model variables v

(x,y, t)andp

(x,y, t) we have with equations (15.7)

and (15.16) the required prognostic equations for the barotropic model. With the

help of the condition of barotropy ρ = ρ(p

) the barotropic model may be integrated

in principle if proper initial conditions are provided.

It is of great advantage for the numerical integration of the barotropic model

equations that the model variables are independent of height. For practical applica-

tions, however, a suitable connection between the model variables v

(x,y, t)and

(x,y, t) for the behavior of the real atmosphere must be established. For the

surface pressure this connection follows immediately. Consequently, the predicted

horizontal wind should correspond to the surface wind. However, it can hardly

be expected that the model produces a reliable replication of the observed sur-

face wind. Experience shows that the vertical average of the observed wind or the

wind at some intermediate level is a better representation of the large-scale motion

than is the surface wind. Therefore, it may be expected that the two-dimensional

barotropic model will produce more realistic pressure and wind ﬁelds at the 500-

hPa pressure level which is located near the so-called “level of nondivergence”

at which the observed divergence of the wind velocity is negligibly small. Since

the two-dimensional barotropic model is incapable of producing meteorologically

signiﬁcant amounts of divergence, best results should be expected if the model is

applied to the 500-hPa level.

Before closing this section, we will now prove the statement that the horizontal

wind remains height-independent if it is height-independent initially at time t