Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

14.8 Propagation of energy 421
and, after eliminating A
2
by means of (14.86),
F
z
=−
α
s
χk
z
A
2
3
2
ω
2
Br
− χ
2
(14.90)
As expected, the vertical energy transport
F
z
is proportional to the square of the
pressure amplitude.
The next step is to establish the relation between the flow of energy and the
group velocity. For the group velocity, relative to the basic current u
0
, we replace
ω in (14.15b) by χ = ω − u
0
k
x
.Thisgives
c
gr
= c
gr
− u
0
i
1
=∇
k
χ =
∂χ
∂k
x
i
1
+
∂χ
∂k
z
i
3
(14.91)
We will now find the relationship between the flow of energy and the group velocity
for gravity waves. From (14.54) and (14.56) we obtain
χ
2
=
k
2
x
k
2
ω
2
Br
=⇒
∂χ
∂k
x
=
χk
2
z
k
x
k
2
,
∂χ
∂k
z
=−
χk
z
k
2
(14.92)
Hence, for gravity waves we have ω
2
Br
>χ
2
. Owing to this inequality,
equation (14.90) admits a very interesting and useful interpretation. If χ>0
and the wave motion is in the upward direction (k
z
> 0), then the flow of energy
(F
z
< 0) is in the downward direction. If the wave motion is in the downward
direction (k
z
< 0), then the flow of energy is upward (F
z
> 0).
For acoustic waves the situation is different. In this case the directions of the
wave motion and the energy flux are identical. For k
z
< 0wehaveF
z
< 0andfor
k
z
> 0wefindF
z
> 0.
We are now ready to state the relationship between the flow of energy and the
group velocity. On substituting the derivative expressions listed in (14.92) into
(14.91) we find immediately
c
gr
=
χk
z
k
2
k
z
k
x
i
1
− i
3
(14.93)
On combining the components
F
x
and F
z
of the energy flux F,wefind
F =
α
s
A
2
3
2
k
x
χ
i
1
−
χk
z
ω
2
Br
− χ
2
i
3
(14.94)
After eliminating the square of the Brunt–Vaisala frequency in (14.94) with the
help of (14.92), we obtain after some slight rearrangements the equation
F =
k
2
x
α
s
A
2
3
2k
z
χ
k
z
k
x
i
1
− i
3
(14.95)

422 Wave motion in the atmosphere
Comparison of this equation with (14.93) shows that the energy flux and the group
velocity have the same direction so that (14.93) and (14.95) may be combined
to give
F =
α
s
A
2
3
2
k
x
k
z
2
k
χ
2
c
gr
(14.96)
We see that the energy flux and the group velocity are unidirectional. This is true
not only for gravity waves but also for wave motion in general.
14.9 External gravity waves
In this section the atmosphere is modeled by a one-layer, homogeneous, and
incompressible fluid. Surface waves due to gravitational effects closely approximate
ocean waves. Since these waves occur at the outer boundary of the fluid they are
called external gravity waves. For simplicity we again restrict the motion to the
(x,z)-plane so that the waves can propagate along the x-axis only. Since the fluid
is homogeneous and incompressible, we set α
= 0sothatα = α
0
= constant. In
this particular situation the first law of thermodynamics does not apply, so (14.31c)
must be ignored. Thus, the equation system (14.31) reduces to a system of three
equations, given by
(a)
∂u
∂t
+ u
0
∂u
∂x
+ α
0
∂p
∂x
= 0
(b) δ
∂w
∂t
+ u
0
∂w
∂x
+ α
0
∂p
∂z
= 0
(c)
∂u
∂x
+
∂w
∂z
= 0
(14.97)
Again we assume that the perturbed flow may be represented by harmonic waves
but now we admit that the amplitudes A
j
are height-dependent:
u
w
p
=
A
1
(z)
A
2
(z)
ρ
0
A
3
(z)
exp[ik
x
(x − ct)] (14.98)
The density ρ
0
, multiplying the amplitude A
3
, is irrelevant insofar as the solution
is concerned and has been introduced for mathematical convenience.
Substituting (14.98) into (14.97) gives
u
0
− c 01
0 ik
x
δ(u
0
− c)
d
dz
ik
x
d
dz
0
A
1
(z)
A
2
(z)
A
3
(z)
= 0(14.99)

14.9 External gravity waves 423
If ρ
0
had not been included, then the specific volume of the basic state would have
appeared explicitly. Equation (14.99) is a coupled set that can be solved most easily
by means of the operator method. As in the previous cases, we set the determinant
of the coefficient matrix equal to zero,
u
0
− c 01
0 ik
x
δ(u
0
− c)
d
dz
ik
x
d
dz
0
= 0(14.100)
and then evaluate the determinant. The resulting operator
d
2
dz
2
− k
2
x
δ
A
j
(z) = 0(14.101)
applies to all A
j
(j = 1, 2, 3). For the general case δ = 1, the eigenvalues (charac-
teristic values) are ±k
x
so that the solution is of the form
A
j
(z) = C
1
exp(k
x
z) + C
2
exp(−k
x
z)(14.102)
Now we must evaluate the integration constants C
1
and C
2
by applying proper
boundary conditions. We begin with the case A
2
. From (14.98) and (14.102) the
vertical velocity perturbation is given by
w
(z, t) =
C
1
exp(k
x
z) + C
2
exp(−k
x
z)
exp[ik
x
(x − ct)] (14.103)
By applying the kinematic boundary condition (9.43a) and canceling out the form
factor of the harmonic wave exp(ik
x
(x − ct) which cannot be zero, we obtain
w
(0) = 0 = C
1
+ C
2
=⇒ C
1
=−C
2
= A (14.104)
so
A
2
= A[exp(k
x
z) − exp(−k
x
z)] (14.105)
The amplitude A
1
is found from the last equation of (14.99), yielding
A
1
=−
1
ik
x
dA
2
dz
= iA[exp(k
x
z) + exp(−k
x
z)] (14.106)
From the first equation of (14.99) we obtain the amplitude A
3
:
A
3
=−(u
0
− c)A
1
=−iA(u
0
− c)[exp(k
x
z) + exp(−k
x
z)] (14.107)
424 Wave motion in the atmosphere
The next step is to eliminate the integration constant A. This is done by
application of the dynamic boundary condition (9.44c). For a frictionless fluid
and a free material surface, the dynamic boundary condition is given by
p(H ) = 0,
dp
dt
H
= 0(14.108a)
where H is the height of the medium, which varies with the distance x and with
time. Since H in general differs very little from the average height
H of the medium,
we may use the approximate boundary condition
p(
H ) = p
0
(H ) + p
(H ) = 0,
dp
dt
H
=
∂p
∂t
+ u
∂p
∂x
+ w
∂p
∂z
H
= 0
(14.108b)
The required perturbation pressure p
is found by linearizing the previous equation
to give
∂p
∂t
+ u
0
∂p
∂x
+ w
∂p
0
∂z
H
= 0(14.109)
If the pressure p
0
of the basic field were permitted to vary with x, an acceleration of
the flow in the x-direction would have to take place, in contrast to the assumption
that u
0
is constant. For this reason the pressure gradient of the basic field in the
x-direction must be set equal to zero, that is ∂p
0
/∂x = 0.
After substituting for p
according to (14.98), using (14.107), we find
−k
x
c(u
0
− c) + k
x
u
0
(u
0
− c) − g tanh(k
x
H ) = 0(14.110)
since the constant A cancels out. The phase speed of the surface gravity waves
propagating in the x-direction is then given by
c = u
0
±
g
k
x
tanh(k
x
H )(14.111)
Two special cases of external gravity waves forming at the free surface are of
particular interest.
14.9.1 Case I
Suppose that the lateral extent of the disturbance L
x
is very large in comparison
with the depth H of the homogeneous layer, i.e. L
x
H . In this case the argument
of the hyperbolic tangent approaches zero. From the Taylor expansion of tanh we
then find
lim
k
x
H →0
tanh(k
x
H ) = k
x
H (14.112)
14.9 External gravity waves 425
so the phase speed of the so-called shallow-water waves or long waves is given by
c = u
0
±
gH if H L
x
(14.113)
This formula, first given by Lagrange, is correct to within one percent if
H<
0.024L
x
. For the homogeneous atmosphere we may replace the argument gH by
R
0
T
0
so that the phase speed is given by
c = u
0
±
R
0
T
0
(14.114)
In the absence of the basic current u
0
the long waves propagate with the Newton
speed of sound c
N
=
√
R
0
T
0
, which is only slightly less than the Laplace speed of
sound c
L
.
14.9.2 Case II
Suppose that the depth of the fluid medium is large in comparison with the
horizontal extent of the disturbance, i.e. L
x
H . In this case the hyperbolic
tangent approaches the value 1, so the phase speed of the so-called deep-water
wave is given by
c = u
0
±
gL
x
2π
if
H L
x
(14.115)
This formula may be used with an error of about one percent if
H>0.4L
x
.Forthe
linear theory it is possible to determine the trajectories (orbits) of the fluid particles
for progressive waves; see LeM
´
ehaute (1976). For the shallow-water waves the
fluid-particle trajectories are elongated ellipses whereas for the deep-water waves
they are nearly circular.
Case I dealing with L
x
H is equivalent to the hydrostatic approximation.
To confirm this, we set δ = 0 in (14.101) and obtain the simple second-order
differential equation
d
2
A
2
dz
2
= 0(14.116)
which can be integrated to give the linear profile
A
2
(z) = D
1
z + D
2
(14.117)
so the vertical velocity perturbation is given by
w
(z) = (D
1
z + D
2
)exp[ik
x
(x − ct)] (14.118)
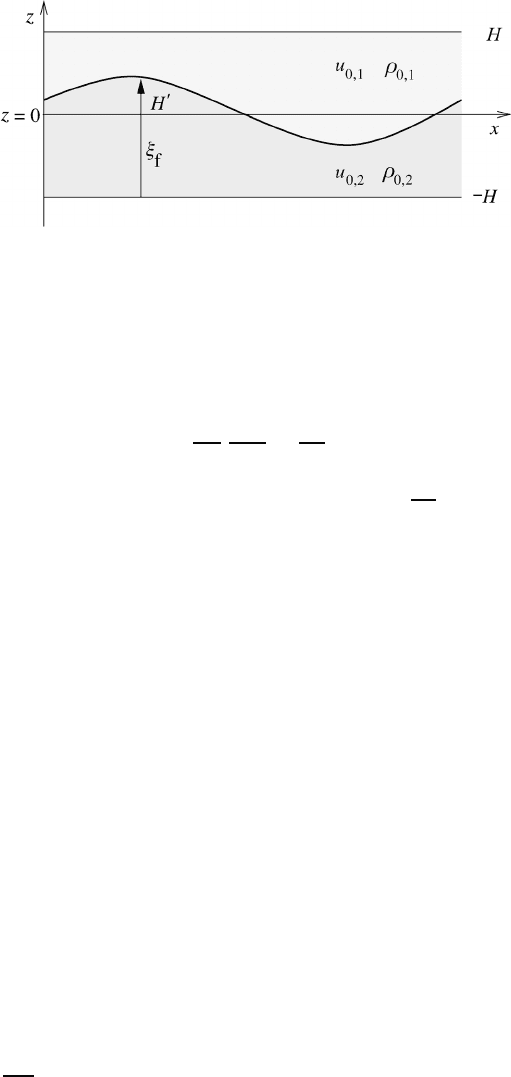
426 Wave motion in the atmosphere
Fig. 14.5 Formation of an internal gravity wave on a zeroth-order discontinuity surface
of density and velocity.
Proceeding as above, we find D
2
= 0. Putting D
1
= D, we obtain
(a) A
2
= Dz
(b) A
1
=−
1
ik
x
dA
2
dz
=
iD
k
x
(c) A
3
=−(u
0
− c)A
1
=−(u
0
− c)
iD
k
x
(14.119)
wherein (14.119b), and (14.119c) follow from (14.99). Knowing A
3
, we also know
p
from (14.98). On substituting p
into the linearized dynamic boundary condi-
tion (14.109) the remaining constant D cancels out and we obtain, as expected,
equation (14.113).
14.10 Internal gravity waves
We are going to deepen our understanding of gravity waves by discussing internal
gravity waves, which may develop on a zeroth-order discontinuity surface both
for density and for velocity. Waves of this type are known as Helmholtz waves.
The theory presented here has also been worked out for less restrictive conditions,
under which the density may vary in a simple manner; see, for example, Gossard
and Hooke (1975). The situation is depicted in Figure 14.5 stating the terminology
which is used.
Again we are dealing with the solution to equation (14.101), which must be
obtained for each of the two layers k = 1, 2:
d
2
dz
2
− k
2
x
A
j,k
(z) = 0,j= 1, 2, 3,k= 1, 2(14.120)
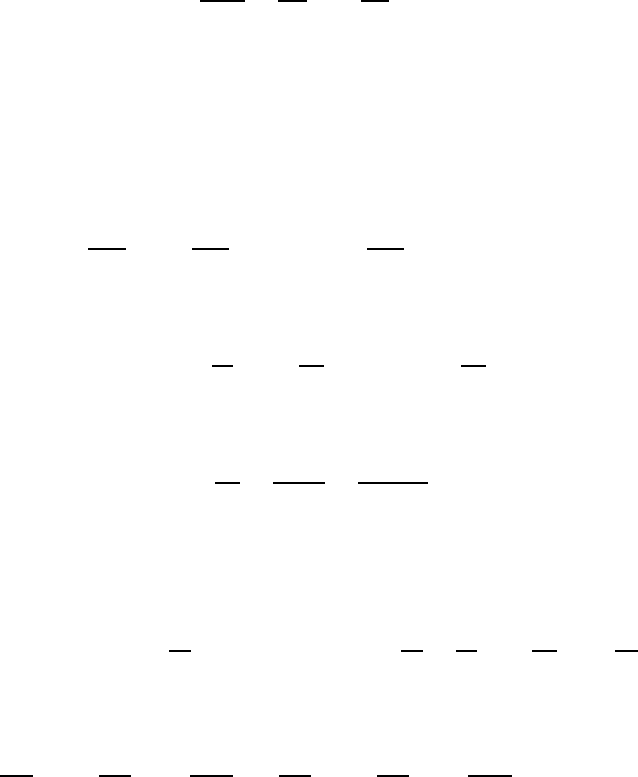
14.10 Internal gravity waves 427
The required kinematic boundary conditions for the two rigid boundaries at z = H
and z =−H are
z = H : w
1
= 0,z=−H : w
2
= 0(14.121)
while the vertical velocity at the discontinuity surface is given by equation (9.41).
Setting the generalized height ξ
f
= H + H
(x,t), see Figure 14.5, we find
w
k
=
d
k
H
dt
=
∂ξ
f
∂t
+ u
k
∂ξ
f
∂x
,k= 1, 2(14.122)
We assume that a wave will form at the boundary and be in phase with the remaining
disturbances. Hence, H
may be written as
H
= A exp[ik
x
(x − ct)] (14.123)
Linearization of (14.122) yields
w
k
=
∂H
∂t
+ u
0,k
∂H
∂x
=−(c − u
0,k
)
∂H
∂x
,k= 1, 2(14.124)
For brevity we also introduce the operator Q
k
:
Q
k
=
∂
∂t
+ u
0,k
∂
∂x
=−(c − u
0,k
)
∂
∂x
(14.125)
By forming the ratio of the perturbations of the vertical velocity for the two layers
we find
w
1
w
2
=
Q
1
H
Q
2
H
=
c − u
0,1
c − u
0,2
(14.126)
indicating that this ratio involves the phase speed and the two constant horizontal
velocities of the basic unperturbed fluid currents. This ratio will be needed shortly.
Next we apply the dynamic boundary condition at the interface:
p
1
− p
2
= 0,
d
k
dt
(p
1
− p
2
) = 0with
d
k
dt
=
∂
∂t
+ u
k
∂
∂x
+ w
k
∂
∂z
(14.127)
Application of the Bjerkness linearization rule gives
∂p
1
∂t
+ u
0,k
∂p
1
∂x
+ w
k
∂p
0,1
∂z
−
∂p
2
∂t
+ u
0,k
∂p
2
∂x
+ w
k
∂p
0,2
∂z
= 0
or Q
k
(p
1
− p
2
) − g(ρ
0,1
− ρ
0,2
)w
k
= 0
(14.128)
where the hydrostatic equation has been used to obtain the second relation.
428 Wave motion in the atmosphere
We are now ready to determine the perturbations of the vertical velocities in each
layer. The solution of (14.120) is analogous to (14.103), so the vertical perturbations
are given by
w
1
(z) = A
2,1
(z)exp[ik
x
(x − ct)]
= [C
1
exp(k
x
z) + C
2
exp(−k
x
z)] exp[ik
x
(x − ct)]
w
2
(z) = A
2,2
(z)exp[ik
x
(x − ct)]
= [D
1
exp(k
x
z) + D
2
exp(−k
x
z)] exp[ik
x
(x − ct)]
(14.129)
The constants C
1
,C
2
,D
1
,andD
2
will now be determined from the boundary
conditions. Application of the kinematic boundary condition (14.121) to the first
equation of (14.129) requires that A
2,1
(H ) = 0, from which
C
1
exp(k
x
H ) =−C
2
exp(−k
x
H ) = C/2(14.130)
follows immediately. Therefore, the amplitude A
2,1
(z)isgivenby
A
2,1
(z) =
C
2
{exp[k
x
(z − H )] − exp[−k
x
(z − H )]}=C sinh[k
x
(z − H )]
(14.131)
Expanding the hyperbolic sine function and contracting the constants gives for the
disturbance w
1
w
1
(z) = A[sinh(k
x
z) − tanh(k
x
H )cosh(k
x
z)] exp[ik
x
(x − ct)]
with A = C cosh(k
x
H ) = constant
(14.132)
Application of the kinematic boundary condition (14.121) for the lower layer
results in
D
1
exp(−k
x
H ) =−D
2
exp(k
x
H ) = D/2(14.133)
and
A
2,2
(z) =
D
2
{exp[k
x
(z + H )] − exp[−k
x
(z + H )]}=D sinh[k
x
(z + H )]
(14.134)
Hence, the perturbation velocity w
2
may be written as
w
2
(z) = B[sinh(k
x
z) + tanh(k
x
H )cosh(k
x
z)] exp[ik
x
(x − ct)]
with B = D cosh(k
x
H ) = constant
(14.135)
In order to find a relation between the integration constants A and B, we form the
ratio (14.126) and obtain
w
1
(z = 0)
w
2
(z = 0)
=−
A
B
=
c − u
0,1
c − u
0,2
=⇒ (c − u
0,2
)A + (c − u
0,1
)B = 0(14.136)
14.10 Internal gravity waves 429
For the determination of the phase speed c of the wave we need another relation
between the constants A and B. To obtain this relation we apply the linearized
dynamic boundary condition (14.128) to the layer k = 1. From (14.125) we have
Q
1
(p
1
− p
2
) =−(c − u
0,1
)
∂
∂x
(p
1
− p
2
)
=−(c − u
0,1
)
−ρ
0,1
∂
∂t
+ u
0,1
∂
∂x
u
1
+ ρ
0,2
∂
∂t
+ u
0,2
∂
∂x
u
2
=−(c − u
0,1
)
ρ
0,1
(c − u
0,1
)
∂u
1
∂x
− ρ
0,2
(c − u
0,2
)
∂u
2
∂x
(14.137)
The pressure gradient for each layer has been eliminated with the help of the
original perturbation equation (14.97a). Using the continuity equation (14.97c)
together with (14.128) in (14.137), we find
−(c − u
0,1
)
−ρ
0,1
(c − u
0,1
)
∂w
1
∂z
+ ρ
0,2
(c − u
0,2
)
∂w
2
∂z
= g(ρ
0,1
− ρ
0,2
)w
1
(14.138)
Had we used k = 2 in (14.128), then, owing to (14.126) we would have obtained
the same result.
The vertical partial derivatives of the perturbation velocities w
1
and w
2
at the
boundary z = 0 follow from (14.132) and (14.135):
∂w
1
∂z
z=0
= k
x
A exp[ik
x
(x − ct)],
∂w
2
∂z
z=0
= k
x
B exp[ik
x
(x − ct)]
(14.139)
By substituting these expressions into (14.138) we obtain the second relation
between A and B:
(c − u
0,1
)
2
ρ
0,1
k
x
+ g(ρ
0,1
− ρ
0,2
)tanh(k
x
H )
A − (c − u
0,1
)(c − u
0,2
)ρ
0,2
k
x
B = 0
(14.140)
Together with equation (14.136) we now have two homogeneous equations for the
unknowns A and B. Arranged in matrix form we may write
(c − u
0,1
)
2
ρ
0,1
k
x
+ g(ρ
0,1
− ρ
0,2
) tanh(k
x
H ) −(c − u
0,1
)(c − u
0,2
)ρ
0,2
k
x
c − u
0,2
c − u
0,1
×
A
B
= 0
(14.141)
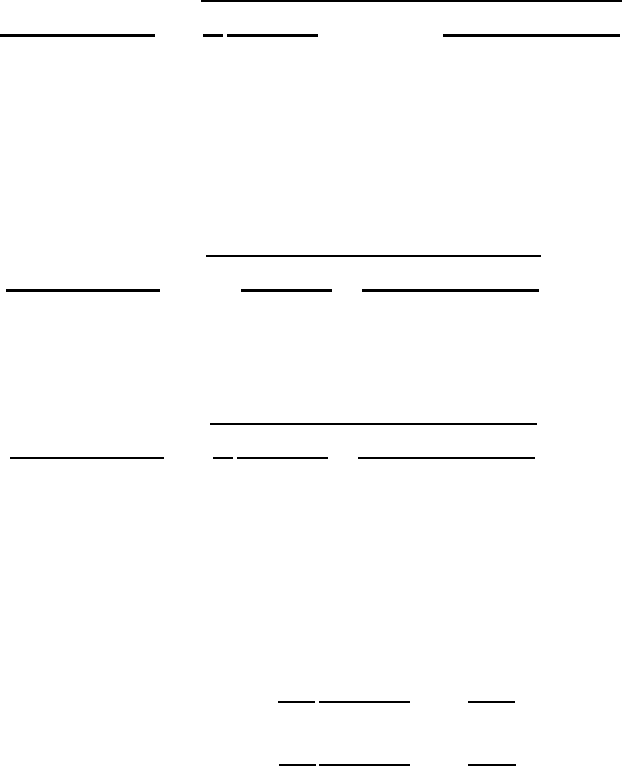
430 Wave motion in the atmosphere
Nonzero values of the integration constants A and B are possible only if the
determinant of the matrix of this expression vanishes. Evaluating the determinant
yields the two roots of the phase speed of the wave at the interface between the two
fluid layers:
c
1,2
=
ρ
0,1
u
0,1
+ ρ
0,2
u
0,2
ρ
0,1
+ ρ
0,2
±
g
k
x
ρ
0,2
− ρ
0,1
ρ
0,1
+ ρ
0,2
tanh(k
x
H ) −
ρ
0,1
ρ
0,2
(u
0,1
− u
0,2
)
2
(ρ
0,1
+ ρ
0,2
)
2
(14.142)
The first term is known as the convective term while the square root is known as the
dynamic term. Owing to the complexity of this equation we will consider special
cases that are more easily interpreted than the original equation.
First of all, it will be noticed that (14.142) reduces to the one-layer solution
(14.111) on setting ρ
0,1
= 0. For shallow-water waves, L
x
H ,wefind
c
1,2
=
ρ
0,1
u
0,1
+ ρ
0,2
u
0,2
ρ
0,1
+ ρ
0,2
±
gH
ρ
0,2
− ρ
0,1
ρ
0,1
+ ρ
0,2
−
ρ
0,1
ρ
0,2
(u
0,1
− u
0,2
)
2
(ρ
0,1
+ ρ
0,2
)
2
(14.143)
which reduces to (14.113) if ρ
0,1
= 0.
For deep-water waves, L
x
H ,wefind
c
1,2
=
ρ
0,1
u
0,1
+ ρ
0,2
u
0,2
ρ
0,1
+ ρ
0,2
±
g
k
x
ρ
0,2
− ρ
0,1
ρ
0,1
+ ρ
0,2
−
ρ
0,1
ρ
0,2
(u
0,1
− u
0,2
)
2
(ρ
0,1
+ ρ
0,2
)
2
(14.144)
which reduces to (14.115) for ρ
0,1
= 0.
Inspection of (14.142) shows that the expression under the square root might be
negative, giving a complex value for the phase speed of the wave. Whenever this
happens the wave is said to be unstable. The conditions for stable and unstable
wave motion are given by
Stable waves: (u
0,1
− u
0,2
)
2
≤
gL
x
2π
ρ
2
0,2
− ρ
2
0,1
ρ
0,1
ρ
0,2
tanh
2πH
L
x
Unstable waves: (u
0,1
− u
0,2
)
2
>
gL
x
2π
ρ
2
0,2
− ρ
2
0,1
ρ
0,1
ρ
0,2
tanh
2πH
L
x
(14.145)
Unstable Helmholtz waves are known as Kelvin–Helmholtz waves.
We conclude this section by considering three special cases that follow from
inspection of (14.142). If the velocities of the basic currents in each layer are equal
but the densities differ, that is u
0,1
= u
0,2
,ρ
0,1
= ρ
0,2
, then the wave is unstable
only if the density of the upper layer exceeds the density of the lower layer. The
result is obvious since overturning would take place immediately. If the densities in
