Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


15.3 The filtered barotropic model 451
which replaces the continuity equation (15.23). Equation (15.65) and the equation
of motion
∂v
h
∂t
q
i
h
+ v
h
·∇
h
v
h
+ f i
3
× v
h
=−∇
h
φ (15.66)
constitute the basic predictive system. The physical model described by this mathe-
matical system consists of a rotating homogeneous incompressible fluid embedded
between two plane-parallel plates. Owing to the incompressibility of the fluid,
vertical motion cannot take place, so the horizontal divergence D
h
vanishes. Thus
we are dealing with frictionless purely horizontal motion. The upper surface is
no longer a free surface where the pressure vanishes. Instead, the pressure at the
top of the fluid layer must differ from zero and be changing, for example, in the
y-direction so that a basic current in the x-direction may form. At the top of the
fluid the geopotential can be interpreted as
p/ρ plus an irrelevant constant. This
simple physical model would require that some pistons are part of the upper plate
so that the pressure may be varied horizontally.
The system (15.65) and (15.66) is unsuitable for the numerical integration.
Instead, we should use the balance equations (15.64a) and (15.64b), extending
their validity to all times t ≥ 0, i.e.
−2J (u, v) +∇
h
· (f i
3
× v
h
) =−∇
2
h
φ, t ≥ 0(15.67a)
or utilize the stream function
2J
∂ψ
∂x
,
∂ψ
∂y
+∇
h
· (f ∇
h
ψ) =∇
2
h
φ, t ≥ 0 (15.67b)
together with the equation of motion (15.66) as the prognostic system.
Nevertheless, due to computer limitations, numerical errors resulting in small
amounts of divergence may occur. To avoid this type of numerical problem it is
customary to integrate the barotropic vorticity equation
∂ζ
∂t
+ v
h
·∇
h
η = 0 with η = ζ + f (15.68)
which is repeated from (10.147), instead of the equation of motion. By introducing
the stream function (15.60) into the definition of the relative vorticity, we obtain
ζ =
∂v
∂x
−
∂u
∂y
=
∂
2
ψ
∂x
2
+
∂
2
ψ
∂y
2
=∇
2
h
ψ (15.69)
Substituting this equation into (15.68) gives the divergence-free vorticity equation
∇
2
h
∂ψ
∂t
+
∂ψ
∂x
∂
∂y
∇
2
h
ψ + f
−
∂ψ
∂y
∂
∂x
∇
2
h
ψ + f
= 0(15.70)

452 The barotropic model
which may be rewritten as
∇
2
h
∂ψ
∂t
+ J
ψ, ∇
2
h
ψ + f
= 0
(15.71)
This equation and the balance equation (15.67b) constitute the prognostic system
of the filtered model. The entire prognostic process is taken care of by the vorticity
equation (15.71) with the prediction variable ψ. Since only ψ appears, one must
solve a Poisson equation for each time step. Equation (15.67b) is used only if
information about the pressure field which is represented by the geopotential field
is desired.
Because the filtered model does not permit the appearance of noise processes
there is no exchange of potential and kinetic energy. Therefore, in a materially
closed region the total kinetic energy must be conserved. Which energetic changes
are still possible in the filtered model? Apparently only those processes which
redistribute kinetic energy between waves and vortices of differing dimensions are
permitted. Charney et al. (1950) used (15.71) to carry out successfully numerical
forecasts.
Summarizing, we may say that the unfiltered and the filtered barotropic models
are different in principle. Therefore, it is quite surprising that these two models
produce nearly the same predictions. This justifies the filtering of noise waves.
15.4 Barotropic instability
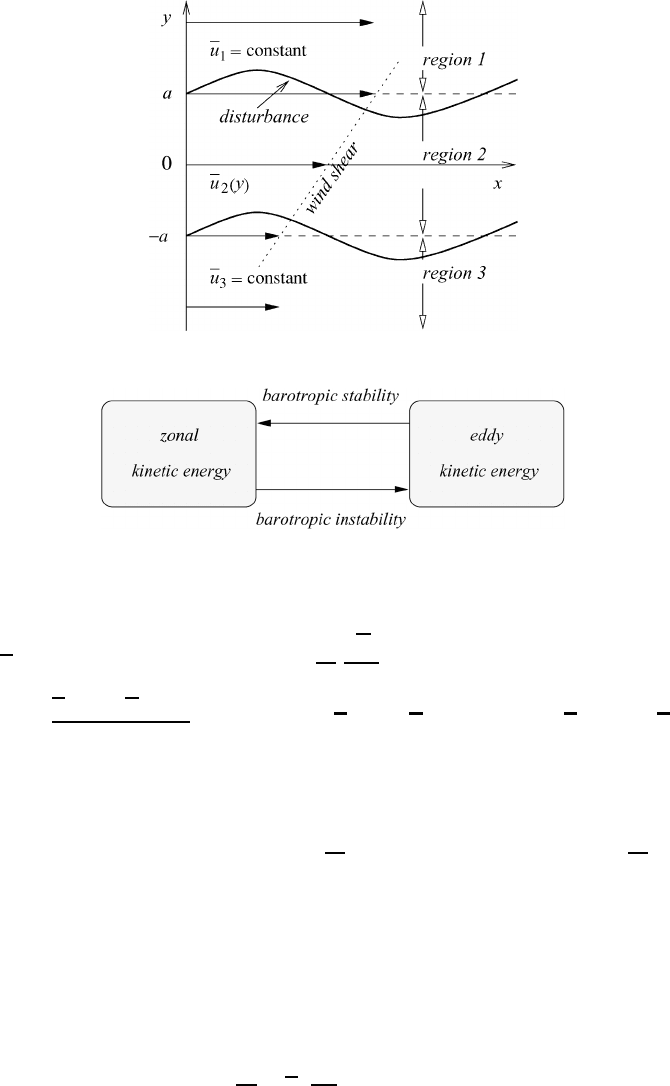
15.4.1 Shearing instability as a limiting case of barotropic instability
Again we consider the previous case in which the constant-density barotropic fluid
is embedded between two plane-parallel plates so that the horizontal divergence
D
h
= 0. We must imagine that the pressure variation is imposed at the top of the
model. We assume that the basic current is directed parallel to the positive x-axis
and that the region of flow along the y-axis extends to infinity in the positive and
negative directions as shown in Figure 15.3. Between y =−a and y = a the model
assumes that we have a linear wind shear, thus dividing the flow region into three
subregions. Since the basic current is in the x-direction, in each of the three regions
the mean geopotential
φ
j
,j= 1, 2, 3, cannot vary in the x-direction, otherwise
there would be a mean flow in the y-direction. Again the Coriolis parameter is
held constant within the entire region. It should be expected that a disturbance of
the flow field will occur in the shear region. For the three regions j = 1, 2, 3the
15.4 Barotropic instability 453
Fig. 15.3 Formation of a wave in the shearing zone.
Fig. 15.4 Barotropic stability and instability.
horizontal flow field is given by
u
j
= u
j,0
+ u
j,1
yu
j,0
=−
1
f
0
∂φ
j
∂y
= constant
j
u
1,1
= u
3,1
= 0
u
2,1
=
u
2
(a) − u
2
(−a)
2a
u
2
(a) = u
1
u
2
(−a) = u
3
(15.72)
Since the fluid is bounded by the lower and the upper plate there is no available
potential energy. The only transformation of energy which is possible is an exchange
of kinetic energy between the vortices, called kinetic energy of the eddies K
,and
the kinetic energy of the zonal current K. If the exchange is from K
to K, one
speaks of barotropic stability. Barotropic instability occurs if the flow of kinetic
energy is in the opposite direction, that is from the zonal current to the eddies. The
situation is displayed schematically in Figure 15.4.
In order to obtain an analytic solution to the problem we must linearize the
horizontal equations of motion (15.27b). For ease of notation we introduce the
operator Q
j
for the three regions:
Q
j
=
∂
∂t
+
u
j
∂
∂x
,j= 1, 2, 3(15.73a)
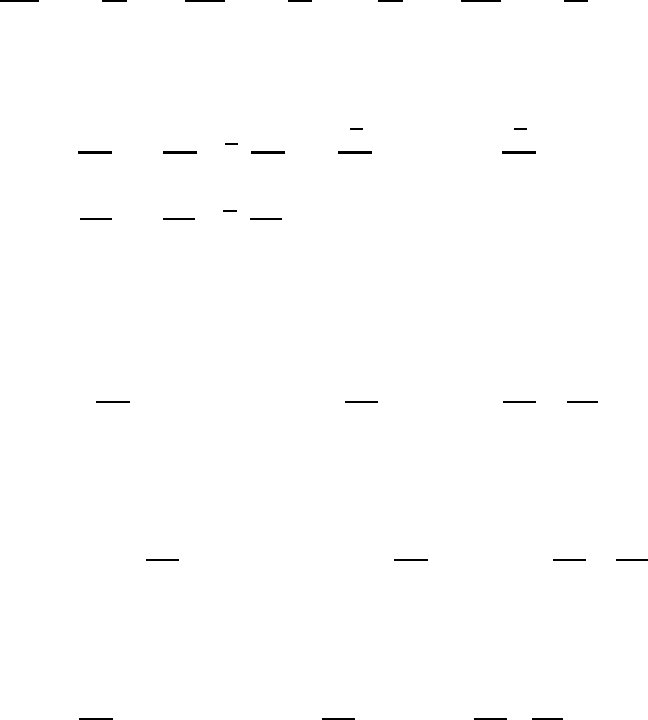
454 The barotropic model
From (15.72) we find
∂Q
1
∂y
= Q
1
∂
∂y
,
∂Q
2
∂y
= Q
2
∂
∂y
+ u
2,1
∂
∂x
,
∂Q
3
∂y
= Q
3
∂
∂y
(15.73b)
Keeping in mind that the basic current is along the x-direction, the individual
derivatives are linearized as
du
j
dt
=
∂u
j
∂t
+
u
j
∂u
j
∂x
+ v
j
∂u
j
∂y
= Q
j
u
j
+ v
j
∂u
j
∂y
dv
j
dt
=
∂v
j
∂t
+
u
j
∂v
j
∂x
= Q
j
v
j
,j= 1, 2, 3
(15.74)
For the three regions we now have to deal with the following set of equations:
Region 1
Q
1
u
1
=−
∂φ
1
∂x
+ f
0
v
1
,Q
1
v
1
=−
∂φ
1
∂y
− f
0
u
1
,
∂u
1
∂x
+
∂v
1
∂y
= 0
(15.75a)
Region 2
Q
2
u
2
+ u
2,1
v
2
=−
∂φ
2
∂x
+ f
0
v
2
,Q
2
v
2
=−
∂φ
2
∂y
− f
0
u
2
,
∂u
2
∂x
+
∂v
2
∂y
= 0
(15.75b)
Region 3
Q
3
u
3
=−
∂φ
3
∂x
+f
0
v
3
,Q
3
v
3
=−
∂φ
3
∂y
−f
0
u
3
,
∂u
3
∂x
+
∂v
3
∂y
= 0(15.75c)
In each region the condition of vanishing divergence has been added. In this set
there are six unknown variables (u
j
,v
j
,j= 1, 2, 3), requiring six conditions in
order to solve the problem. These conditions are the behaviors of the solution at
y =±∞, two kinematic boundary-surface conditions at y =±a, and two dynamic
boundary-surface conditions at y =±a.
Instead of using the equations of motion directly, it is easier to find the solution
to the problem (15.75) by employing the barotropic vorticity equation. This can be
done directly by linearizing (15.68) and keeping in mind that the mean geopotential
cannot vary in the x-direction. In each region we are going to obtain the linearized
vorticity equation by taking the partial derivative with respect to x of the second
15.4 Barotropic instability 455
equation of motion and subtracting the partial derivative with respect to y of the
first equation. For the second region this will now be demonstrated. From (15.73b)
and (15.75b) we find
Q
2
∂u
2
∂y
+ u
2,1
∂u
2
∂x
+ u
2,1
∂v
2
∂y
=−
∂
2
φ
2
∂x ∂y
+ f
0
∂v
2
∂y
Q
2
∂v
2
∂x
=−
∂
2
φ
2
∂x ∂y
− f
0
∂u
2
∂x
(15.76)
Subtraction results in
Q
2
∂v
2
∂x
−
∂u
2
∂y
− u
2,1
∂u
2
∂x
+
∂v
2
∂y
=−f
0
∂u
2
∂x
+
∂v
2
∂y
(15.77)
Since the divergence must vanish, we find
Q
2
∂v
2
∂x
−
∂u
2
∂y
= 0(15.78)
Hence, the Q
2
term is operating on the vorticity of this region. With the help
of (15.75a) and (15.75c) it may easily be verified that one obtains analogous
expressions for regions 1 and 3 so that in general we have
Q
j
∂v
j
∂x
−
∂u
j
∂y
= 0,j= 1, 2, 3(15.79)
This equation can also be written in the form dη
j
/dt = 0sothatvorticityis
conserved. The physically interesting solution in connection with the problem at
hand is to set the vorticity itself equal to zero:
∂v
j
∂x
−
∂u
j
∂y
= 0,j= 1, 2, 3(15.80)
On differentiating this equation with respect to x and the divergence condition with
respect to y, we find upon elimination of the mixed partial derivatives the Laplace
equation
∂
2
v
j
∂x
2
+
∂
2
v
j
∂y
2
= 0,j= 1, 2, 3(15.81)
which must hold in each region j. We assume the validity of a solution of the form
v
j
= V
j
(y) exp[ik
x
(x − ct)],j= 1, 2, 3(15.82)
If the phase speed c happens to be real, then the solution corresponds to a stable
wave. If c is complex then the amplitude will grow and barotropic instability will
occur. We will now state the solution conditions.
456 The barotropic model
(1) Lateral boundary conditions at infinity:
y =∞: v
1
= 0,y=−∞: v
3
= 0
(15.83)
(2) Kinematic boundary conditions at y =±a
The kinematic boundary condition (9.41) also applies to the horizontal situation.
Therefore, we may write for region 1 and 2 at y = a the conditions for the
generalized y-coordinate ξ
a
:
v
1
(a) =
∂ξ
a
∂t
+ u
1,0
∂ξ
a
∂x
,v
2
(a) =
∂ξ
a
∂t
+ u
2,0
∂ξ
a
∂x
(15.84a)
Analogously we find the kinematic boundary condition at y =−a:
v
2
(−a) =
∂ξ
−a
∂t
+ u
2,0
∂ξ
−a
∂x
,v
3
(−a) =
∂ξ
−a
∂t
+ u
3,0
∂ξ
−a
∂x
(15.84b)
Since u
1,0
=u
2,0
at y =a and u
2,0
=u
3,0
at y =−a, we find the kinematic boundary
conditions at y =±a:
v
1
(a) = v
2
(a),v
2
(−a) = v
3
(−a)
(15.85)
(3) Dynamic boundary conditions at y =±a
The dynamic boundary condition, see Section 9.5, requires that the pressure
must be continuous across the boundary in order to prevent infinitely large forces
occurring. In the present situation the pressure is represented by the geopotential.
Therefore, we may write the dynamic boundary conditions in the form
y = a:
d
dt
(φ
1
− φ
2
) = 0,y=−a:
d
dt
(φ
2
− φ
3
) = 0(15.86)
or, expanded and linearized for each side, as
dφ
j
dt
=
∂φ
j
∂t
+
u
j
∂φ
j
∂x
+ v
j
∂φ
j
∂y
,j= 1, 2, 3(15.87)
This form follows upon recalling that the averaged geopotential does not vary in
the x-direction. By taking the partial derivative with respect to x of this expression,
for each j we find
∂
∂x
dφ
j
dt
=
∂
∂x
∂
∂t
+
u
j
∂
∂x
φ
j
+
∂
∂x
v
j
∂φ
j
∂y
= Q
j
∂φ
j
∂x
+
∂
φ
j
∂y
∂v
j
∂x
(15.88)
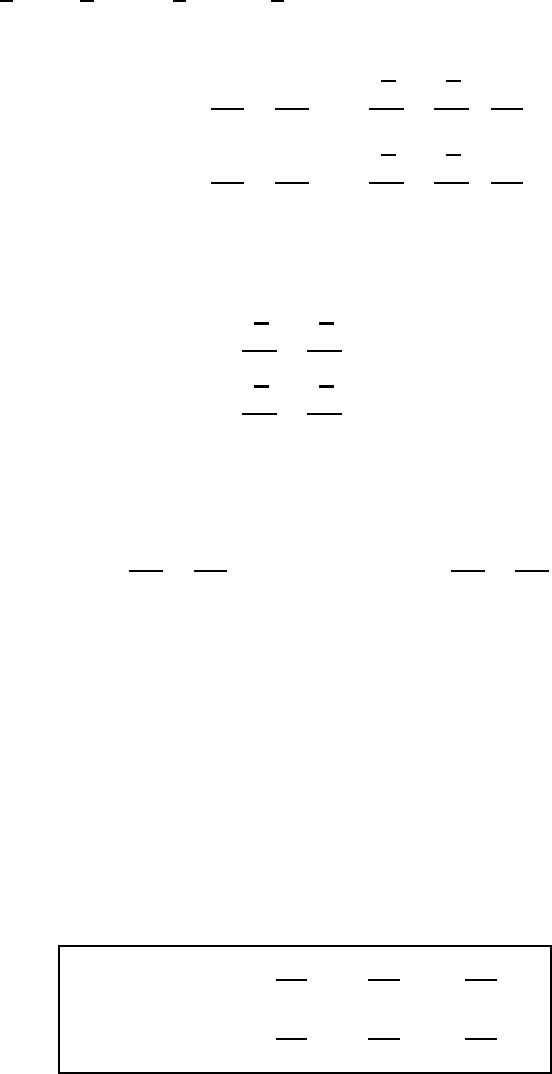
15.4 Barotropic instability 457
Inspection of Figure 15.4 shows that, at y =±a, the basic currents coincide, that
is u
1
(a) = u
2
(a)andu
2
(−a) = u
3
(−a), so that Q
1
(a) = Q
2
(a)andQ
2
(−a) =
Q
3
(−a). Thus, the partial derivative with respect to x of (15.86) is given by
y = a: Q
1
∂φ
1
∂x
−
∂φ
2
∂x
+
∂
φ
1
∂y
−
∂
φ
2
∂y
∂v
1
∂x
= 0
y =−a: Q
3
∂φ
2
∂x
−
∂φ
3
∂x
+
∂
φ
2
∂y
−
∂
φ
3
∂y
∂v
3
∂x
= 0
(15.89)
where we have used the kinematic boundary condition (15.85). Owing to the facts
that u
1,0
(a) = u
2,0
(a)andu
2,0
(−a) = u
3,0
(−a), it follows from (15.72) that
y = a:
∂
φ
1
∂y
−
∂
φ
2
∂y
=−f
0
u
1,0
+ f
0
u
2,0
= 0
y =−a:
∂φ
2
∂y
−
∂
φ
3
∂y
=−f
0
u
2,0
+ f
0
u
3,0
= 0
(15.90)
Therefore, in each equation of (15.89) the second term vanishes.
As in the case of (15.79), at y =±a we consider the differential equations
y = a:
∂φ
1
∂x
−
∂φ
2
∂x
= 0,y=−a:
∂φ
2
∂x
−
∂φ
3
∂x
= 0(15.91)
On replacing ∂φ
j
/∂x in these expressions by means of (15.75a) and (15.75b) and
utilizing the kinematic boundary conditions (15.85) we obtain
y = a: −Q
1
u
1
+ Q
2
u
2
+ u
2,1
v
2
= 0
y =−a: −Q
2
u
2
+ Q
3
u
3
− u
2,1
v
2
= 0
(15.92)
Since the Laplace equation (15.81), which needs to be solved, is expressed in the
variable v
j
, we must eliminate the variables u
j
in terms of the variables v
j
of
the filtering condition stated for each region. This task is accomplished by partial
differentiation of (15.92) with respect to x and then replacing ∂u
j
/∂x by −∂v
j
/∂y
since D
h
= 0. This results in the dynamic boundary conditions
(a) y = a: Q
1
∂v
1
∂y
− Q
2
∂v
2
∂y
+ u
2,1
∂v
2
∂x
= 0
(b) y =−a: Q
2
∂v
2
∂y
− Q
3
∂v
3
∂y
− u
2,1
∂v
2
∂x
= 0
(15.93)

458 The barotropic model
We are now ready to determine the phase velocity of the disturbance. Substitution
of (15.82) into (15.81) gives the ordinary linear differential equation
d
2
V
j
dy
2
− k
2
x
V
j
= 0,j= 1, 2, 3(15.94)
which can easily be solved by standard methods. The characteristic values of this
equation are k
x
and −k
x
, so the solution for each of the three regions can be written
down immediately as
V
j
= A
j
exp(−k
x
y) + B
j
exp(k
x
y),j= 1, 2, 3(15.95)
The constants B
1
and A
3
must vanish in order to keep the solution bounded for
y −→ ±∞. Using the trial solution (15.82) for (15.81), we obtain the perturbation
velocities
v
1
= A
1
exp(−k
x
y)exp[ik
x
(x − ct)]
v
2
= [A
2
exp(−k
x
y) + B
2
exp(k
x
y)] exp[ik
x
(x − ct)]
v
3
= B
3
exp(k
x
y)exp[ik
x
(x − ct)]
(15.96)
which still contain the unknown constants A
1
,A
2
,B
2
,B
3
. Owing to the kinematic
boundary surface conditions (15.85) we find the following relations among the
remaining constants:
y = a: v
1
= v
2
=⇒ A
1
exp(−k
x
a) = A
2
exp(−k
x
a) + B
2
exp(k
x
a)
y =−a: v
2
= v
3
=⇒ B
3
exp(−k
x
a) = A
2
exp(k
x
a) + B
2
exp(−k
x
a)
(15.97)
So far we have used the conditions at infinity and the kinematic boundary condi-
tions.
Now we are going to involve equations (15.93), which resulted from the dynamic
boundary conditions. We will show how to evaluate (15.93a). For y = a we need
to substitute the expressions
Q
1
∂v
1
∂y
y=a
= ik
2
x
(c − u
1
)A
1
exp(−k
x
a)exp[ik
x
(x − ct)]
Q
2
∂v
2
∂y
y=a
= ik
2
x
(c − u
1
)[A
2
exp(−k
x
a) − B
2
exp(k
x
a)] exp[ik
x
(x − ct)]
(15.98)
into (15.93a). The constant A
1
exp(−k
x
a) can be replaced by means of (15.97).
After some easy manipulations we obtain the upper equation of the matrix system
u
2,1
exp(−k
x
a)[2k
x
(c − u
1
) + u
2,1
]exp(k
x
a)
[2k
x
(c − u
3
) − u
2,1
] exp(k
x
a) −u
2,1
exp(−k
x
a)
A
2
B
2
= 0
(15.99)
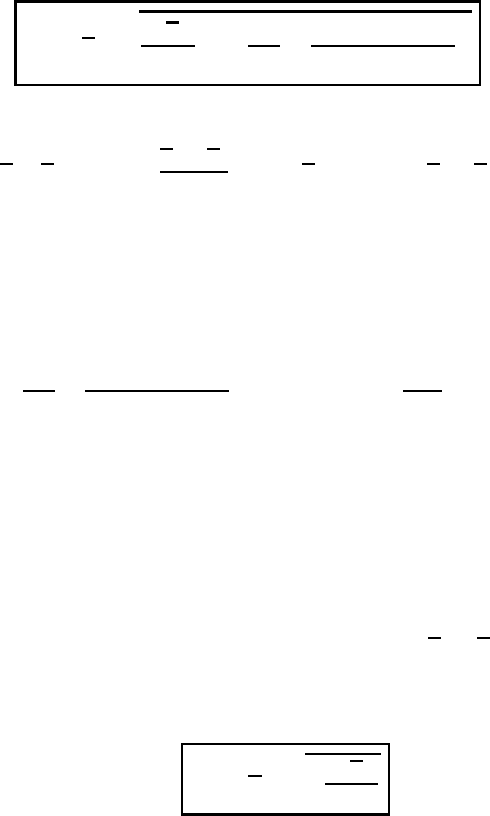
15.4 Barotropic instability 459
In complete analogy the lower equation of this system has been obtained from
(15.93b), wherein now the constant B
3
exp(−k
x
a) has been replaced with the help
of (15.97).
Nonzero values of A
2
and B
2
are possible only if the determinant of the homoge-
neous equations (15.99) vanishes. On solving the determinant of this two-by-two
matrix for the phase velocity we obtain
c
1,2
= u ±
(u)
2
4
1 −
1
ak
x
+
1 − exp(−4k
x
a)
4a
2
k
2
x
(15.100)
where the abbreviations
u = u
2
(y = 0) =
u
1
+ u
3
2
,
u = 2au
2,1
= u
1
− u
3
(15.101)
have been introduced.
Equation (15.100) will now be discussed. If the expression within the large
parentheses is less than zero then the phase velocity will be a complex number so
that barotropic instability occurs. Numerical evaluation of this expression shows
that
1 −
1
ak
x
+
1 − exp(−4k
x
a)
4a
2
k
2
x
< 0fork
x
a =
2aπ
L
x
< 0.64 (15.102)
Since 2a is the width of the shear zone, we see that the ratio of this width
to the wavelength L
x
determines whether the wave is barotropically stable or
not. Broad zones of wind shear with short wavelength of the disturbance are
barotropically stable since they do not satisfy the inequality occurring in (15.102).
Laterally small zones of wind shear with a large wavelength are barotropically
unstable.
Assume that the shear zone shrinks to zero. In this case a velocity jump occurs
at y = 0, where the basic current abruptly changes from
u
1
to u
3
. Letting a → 0,
we find upon using L’Hospital’s rule or by expanding the exponential at least to
the quadratic term that
c
1,2
= u ±
−
(u)
2
4
(15.103)
Since the phase velocity is always complex this is the unstable solution yielding the
shearing waves. It is noteworthy that the same result has been obtained for gravity
waves at discontinuities by setting u
0,1
= u
0,2
and ρ
0,1
= ρ
0,2
in (14.142).

460 The barotropic model
Fig. 15.5 A continuous velocity profile u(y).
15.4.2 Conditions for the occurrence of barotropic instability
Let us now consider a continuous velocity profile of the basic current; see
Figure 15.5. For the continuous velocity profile it is possible to derive a necessary
condition for the occurrence of barotropic instability. The basic model assumptions
are
∇
h
·v
h
= 0, u = u(y),f= f
0
+ βy, β =
∂f
∂y
= constant (15.104)
Again the barotropic fluid is embedded between two plane-parallel plates so that
no potential energy can be transformed into kinetic energy. The decisive change
in the model assumptions (15.72), apart from the velocity profile, is that now the
Coriolis parameter is permitted to change with y. The parameter β is known as the
Rossby parameter.
Starting with the vorticity equation (15.71) and linearizing the Coriolis parameter
after Rossby, we obtain
∂
∂t
∇
2
h
ψ
+ J
ψ, ∇
2
h
ψ
+ β
∂ψ
∂x
= 0(15.105)
We assume that the stream function varies according to
ψ =
ψ(y) + ψ
(x,y, t)(15.106)
so that the velocity components of the basic current can be expressed by
u =−
∂
ψ
∂y
,
v =
∂
ψ
∂x
= 0(15.107)
