Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

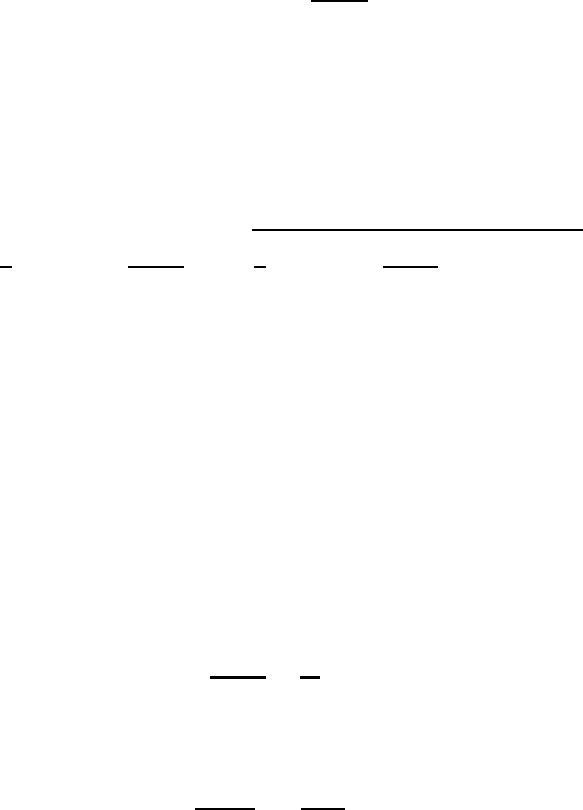
14.5 Sound waves and gravity waves 411
Thus, the partial differential equation (14.42) was transformed into a fourth-degree
algebraic equation for the circular frequency, permitting us to determine the phase
velocities of the various waves.
For δ = 1 representing the general case, equation (14.44) will be investigated
from two points of view. In case (i) the appearance of gravity waves will be
suppressed by setting g = 0; in case (ii) the gravity waves will be admitted.
(i) g = 0
This condition results in
ω
1,2
= 0,ω
3,4
=±k
κR
0
T
0
=±kc
L
(14.45)
From (14.45) it follows that only two waves exist, namely the compressional waves.
Thus, we have repeated the results shown in (14.37a) and (14.37c) for the special
case that u
0
= 0.
(ii) g = 0
Now we obtain the solution
ω
2
1,2
=
1
2
κR
0
T
0
k
2
+
κg
2
4R
0
T
0
±
1
4
κR
0
T
0
k
2
+
κg
2
4R
0
T
0
2
−g
2
(κ − 1)k
2
x
(14.46)
for sound and gravity waves combined. The positive square root results in a solution
for sound waves that are modified by gravitational effects. The negative square root
may be viewed as a solution for gravity waves that are modified by sound effects.
We will conclude this section by considering some additional special cases of
the frequency equation (14.44). These are the effect of incompressibility and the
propagation of sound waves in the horizontal and vertical directions.
14.5.1 The effect of incompressibility
In textbooks on thermodynamics it is shown that, in an incompressible fluid where
the coefficient of piezotropy γ
ρ
p
approaches zero, the Laplace speed of sound c
L
is
infinitely large:
γ
ρ
p
=
1
κR
0
T
0
=
1
c
2
L
= 0(14.47)
On setting δ = 1 in (14.44) and multiplying this equation by the piezotropy
coefficient, we find
γ
ρ
p
ω
4
− ω
2
k
2
+
g
2
4R
2
0
T
2
0
+
g
2
k
2
x
R
0
T
0
− g
2
k
2
x
γ
ρ
p
= 0(14.48)

412 Wave motion in the atmosphere
Permitting the piezotropy coefficient to approach zero to simulate incompressibility,
we find the frequency equation for an incompressible medium to be
−ω
2
R
0
T
0
k
2
+
g
2
4R
0
T
0
+ g
2
k
2
x
= 0(14.49)
Owing to the elimination of sound waves the frequency equation is now only of
second degree and contains gravity waves only. The frequency of the gravity waves
is given by
ω
1,2
=±
g
2
k
2
x
R
0
T
0
k
2
+ g
2
/(4R
0
T
0
)
(14.50)
Now we wish to investigate the effect of static stability on gravity waves. For
this purpose we replace the term κ − 1 in (14.44) by the vertical gradient of the
potential temperature θ
0
. Logarithmic differentiation of the basic-state potential-
temperature equation, assuming that we have isothermal conditions of the basic
state, and application of the hydrostatic equation results in
κ − 1 =
κR
0
T
0
gθ
0
∂θ
0
∂z
(14.51)
Substituting this expression into (14.44), setting δ = 1, and observing that the scale
height is given by H = R
0
T
0
/g,wefind
ω
4
− ω
2
κR
0
T
0
k
2
+
κg
4H
+ k
2
x
g
κR
0
T
0
θ
0
∂θ
0
∂z
= 0(14.52a)
This form of the frequency equation permits us to make a very useful approximation,
which should be valid for a great number of situations. First we form the ratio
κR
0
T
0
k
2
z
[κg/(4H )] with k
2
= k
2
x
+ k
2
z
. If the largest vertical wavelength L
z
does
not significantly exceed the scale height H , as is often the case, this ratio is roughly
150. For L
z
<Hthe ratio is even larger, so that the term κg/(4H ) in (14.52a)
may be dropped in comparison with κR
0
T
0
k
2
without a significant loss of accuracy.
This yields the simplified form
ω
4
− ω
2
κR
0
T
0
k
2
+ k
2
x
g
κR
0
T
0
θ
0
∂θ
0
∂z
= 0(14.52b)
As before, we multiply this equation by the piezotropy coefficient. Permitting this
coefficient to approach zero, we obtain the simplified frequency equation
ω
1,2
=±
k
x
k
g
θ
0
∂θ
0
∂z
,u
0
= 0(14.53)

14.5 Sound waves and gravity waves 413
for the incompressible medium. If u
0
differs from zero, analogously to (14.37c) we
must replace ω
1,2
by
χ
1,2
= ω
1,2
− u
0
k
x
=±
k
x
k
g
θ
0
∂θ
0
∂z
(14.54)
The term χ is known as the intrinsic frequency. In contrast to the circular frequency,
the intrinsic frequency is measured by an observer drifting with the basic air current.
The introduction of χ avoids the explicit appearance of the Doppler effect. The
corresponding phase velocities are then given by
c
1,2
=
ω
1,2
k
=±
k
x
k
2
g
θ
0
∂θ
0
∂z
,u
0
= 0
or c
1,2
=
ω
1,2
k
=
k
x
k
u
0
±
k
x
k
2
g
θ
0
∂θ
0
∂z
(14.55)
One final remark on the approximation used in (14.52) might be helpful. Had we
ignored the term g
2
/(4R
0
T
0
) in comparison with R
0
T
0
k
2
z
in (14.49), we would have
obtained a slightly different approximation.
Inspection of (14.54) shows that, for stable stratification, ∂θ
0
/∂z > 0, stable
oscillations occur. An amplified disturbance occurs for superadiabatic conditions
with ∂θ
0
/∂z < 0sincec
1,2
is complex.
Finally, if the depth of the disturbance is large in comparison with the horizontal
scale, that is k
2
x
k
2
z
,thenk in (14.53) may be approximated by k
x
and we obtain
the Brunt–Vaisala frequency
ω
Br
=
g
θ
0
∂θ
0
∂z
(14.56)
which is usually discussed in connection with oscillations in vertical stability of
isolated air parcels.
Next we wish to show that the system (14.32) contains two special cases
describing sound waves propagating in the horizontal or in the vertical direction.
For simplification we set the basic current u
0
= 0.

414 Wave motion in the atmosphere
14.5.2 Horizontal sound waves
In the basic system (14.32) we set g = 0andw
= 0 to eliminate gravity waves
and vertical motion. This means that the remaining sound wave can propagate only
in the x-direction so that the wave front is parallel to the (y,z)-plane. With these
simplifications (14.32) reduces to the prognostic set
∂u
∂t
+ R
0
T
0
∂q
∂x
= 0,
∂q
∂t
− κ
∂s
∂t
= 0,
∂u
∂x
+
∂s
∂t
= 0(14.57)
By combining the last two expressions we find
∂u
∂t
+ R
0
T
0
∂q
∂x
= 0,
∂u
∂x
+
1
κ
∂q
∂t
= 0(14.58)
from which we determine the perturbation velocity u
and the relative pressure
disturbance q. By employing the operator method we obtain the wave equation for
horizontally propagating sound waves:
∂
2
∂t
2
− κR
0
T
0
∂
2
∂x
2
ψ
j
= 0(14.59)
with (ψ
1
,ψ
2
) = (u
,q). The solution to (14.59), also known as D’Alembert’s
solution, can be written in the general form
ψ
j
= ψ
j
(x ± c
L
t)withc
2
L
= κR
0
T
0
(14.60)
where the disturbances propagate in the positive and negative x-directions with the
speed of sound c
L
.
14.5.3 Vertical sound waves
In the basic system (14.32) we set δ = 1,g= 0, and u
= 0 to suppress gravity
waves and the horizontal velocity. This results in the following system:
∂w
∂t
+ R
0
T
0
∂q
∂z
= 0,
∂q
∂t
− κ
∂s
∂t
= 0,
∂w
∂z
+
∂s
∂t
= 0(14.61)
Eliminating again ∂s/∂t and applying the operator method to the remaining system,
we obtain the wave equation
∂
2
∂t
2
− κR
0
T
0
∂
2
∂z
2
ψ
j
= 0(14.62)
with (ψ
1
,ψ
2
) = (w
,q). The solution is given by
ψ
j
= ψ
j
(z ± c
L
t)(14.63)
showing that the disturbances propagate in the positive and negative vertical
directions with the speed of sound.

14.5 Sound waves and gravity waves 415
14.5.4 Hydrostatic filtering
In the basic set of the linearized equation (14.32) we now set δ = 0. Thus, the
term (∂/∂t + u
0
∂/∂x)w
disappears so that a prognostic equation is replaced by a
diagnostic relation. This corresponds to hydrostatic filtering. Instead of (14.44) the
frequency equation now reads
−ω
2
R
0
T
0
k
2
z
+
g
2
4R
0
T
0
+ g
2
k
2
x
κ − 1
κ
= 0(14.64)
The comparison with the frequency equation (14.49) for an incompressible medium
reveals far-reaching agreement, demonstrating that the hydrostatic approximation
has eliminated to a large extent the effect of compressibility. This can also be seen
by solving (14.64) for ω, yielding
ω
2
= g
2
κ − 1
κ
k
2
x
R
0
T
0
k
2
z
+ g
2
/(4R
0
T
0
)
(14.65)
This expression shows that, for g = 0, not only gravity waves but also sound
waves have completely been eliminated from the system since in this case ω = 0.
Comparison of (14.64) with (14.49) shows that the hydrostatic approximation has
eliminated the quantity k
2
x
in comparison with k
2
z
, meaning that L
x
L
z
.From
Figure 14.4 we recognize that, in the present situation, the angle of inclination of the
wave front is very small, so the horizontal displacement velocity c
h
is much larger
than the phase speed c itself, whose direction is perpendicular to the wave front.
Finally, we wish to show from another point of view that hydrostatic filtering
of the system (14.32) eliminates vertically propagating sound waves. This type of
filtering is very important in numerical weather prediction. The reason for this is
that the time step of integration that can be chosen is inversely proportional to
the phase speed of the fastest waves contained in the system, which are the sound
waves. More information on this topic will be given in the chapter on numerical
procedures in weather prediction.
In order to actually show that the vertically propagating sound waves are filtered
out of the system, we eliminate gravitational effects by setting g = 0andset
u
= 0 in (14.32). Thus, the remaining wave can propagate in the positive or
negative z-direction only. With these assumptions (14.32) reduces to
R
0
T
0
∂q
∂z
= 0,
∂q
∂t
− κ
∂s
∂t
= 0,
∂w
∂z
+
∂s
∂t
= 0,u
0
= 0(14.66)
The first expression implies that the relative pressure disturbance is independent
of height. Nevertheless, q might still be a function of time. If it turns out that q is
a function of time so that ∂q/∂t = 0, then the pressure disturbance occurs at all
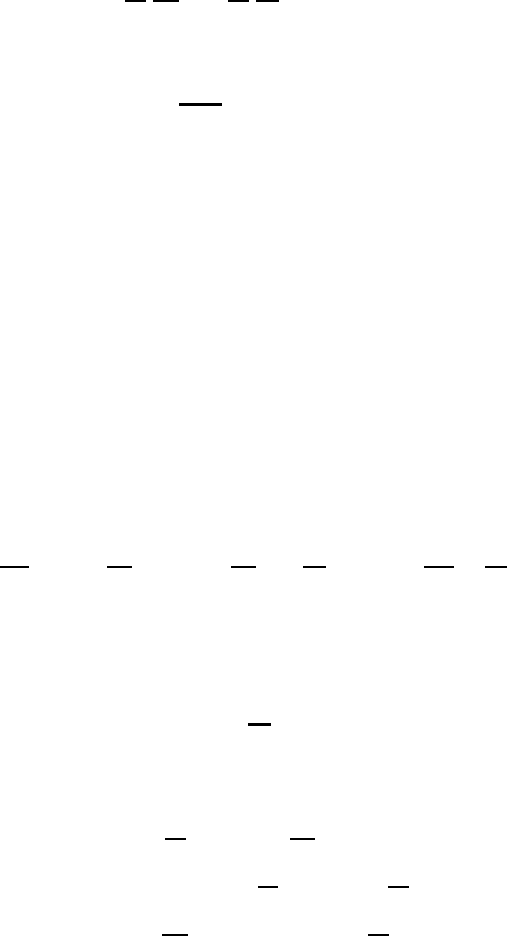
416 Wave motion in the atmosphere
heights simultaneously. This means that the vertical phase speed of the pressure
disturbance is infinitely large, thus leaving the atmosphere immediately.
To look at the problem from a slightly different point of view, we differentiate
the second expression of (14.66) with respect to z and find
∂
∂t
∂q
∂z
= κ
∂
∂t
∂s
∂z
= 0sinceq = q(z)(14.67)
From the third expression of (14.66) it now follows that
∂
2
w
∂z
2
= 0 =⇒ w
= az + b (14.68)
The kinematic boundary condition states that w
(z = 0) = 0, so b = 0. To prevent
w
becoming infinitely large with increasing z,weseta = 0sothatw
= 0.
Therefore, according to (14.66), we have ∂s/∂t = 0 and finally ∂q/∂t = 0, so
q = q(t). Now q is independent of height and time so that there exists no (z, t)-
relation for q, which would be required for a moving wave. We interpret this by
saying that vertically propagating sound waves have been filtered out of the system.
Horizontal sound waves have not been eliminated by hydrostatic filtering. They
may result from a degeneration of horizontal gravity waves, as will be shown next.
14.5.5 Degeneration of horizontal gravity waves
We conclude this section by showing that horizontally propagating gravity waves
may degenerate to sound waves. Setting w
= 0 in the system (14.32), we obtain
with u
0
= 0 the prognostic system
∂u
∂t
+ R
0
T
0
∂q
∂x
= 0,
∂q
∂t
− κ
∂s
∂t
= 0,
∂u
∂x
+
∂s
∂t
= 0(14.69)
consisting of the first equation of motion, the adiabatic equation, and the continuity
equation. Furthermore, due to the hydrostatic filtering, the second row of (14.32)
becomes a diagnostic relation:
R
0
T
0
∂
∂z
− g
q + gs = 0(14.70)
In order to apply the operator method, we form the required determinant:
∂
∂t
R
0
T
0
∂
∂x
0
0
∂
∂t
−κ
∂
∂t
∂
∂x
0
∂
∂t
= 0(14.71)

14.5 Sound waves and gravity waves 417
Expansion of this determinant results in
∂
∂t
∂
2
∂t
2
− c
2
L
∂
2
∂x
2
ψ
j
= 0(14.72)
with (ψ
1
,ψ
2
,ψ
3
) = (u
,q,s). Excluding the trivial solution in which the functions
u
,q,ands are constants, we obtain D’Alembert’s wave equation
∂
2
∂t
2
− c
2
L
∂
2
∂x
2
ψ
j
= 0
(14.73)
whose solution is given by (14.60). This equation shows that the disturbances are
displaced in the positive or the negative x-direction.
Let us now specifically discuss the pressure disturbance q = q(x ± c
L
t,z)in
a little more detail by including the compatibility equation (14.70). Integration of
the second expression of (14.69) with respect to time gives
q
κ
= s + f (x,z, t
0
)(14.74)
where f (x, z,t
0
) is an arbitrary function. Initially, at time t
0
, the relative pressure q
and the relative density s are assumed to be zero so that f is zero also. Substitution
of (14.74) into (14.70) yields
(κ − 1)g
κ
q = R
0
T
0
∂q
∂z
(14.75)
which can be integrated to give
q = Q exp
(κ − 1)gz
κR
0
T
0
= Q exp
(κ − 1)gz
c
2
L
(14.76)
with Q = q(x ± c
L
t,z = 0). Now we introduce the definition of the relative
pressure disturbance q = p
/p
0
into (14.76). We also recall that the basic state
pressure p
0
decays exponentially so that
p
0
= p
0
(z = 0) exp
−
z
H
with H =
R
0
T
0
g
=
c
2
L
κg
(14.77)
Therefore, the pressure disturbance is given by
p
= p
0
(z = 0)Q(x ± c
L
t,z = 0) exp
−
gz
c
2
L
(14.78)
This equation describes the horizontal displacement of a pressure disturbance with
a speed of displacement c
L
. The disturbance decreases with height. At a height of
10 km the disturbance has decreased by about one third of its value at the surface of
the earth. In this special case the pressure disturbance p
decreases exponentially
with height in a horizontally displaced gravity wave that is moving with the speed
of sound.
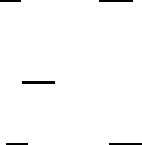
418 Wave motion in the atmosphere
14.6 Lamb waves
By direct substitution it is easily shown that for u
0
= 0 the basic system (14.31) is
satisfied by the following solution:
u
= S exp
z
H
exp
−
z
κH
exp[ik
x
(x − c
L
t)]
w
= 0
p
= P exp
−
z
κH
exp[ik
x
(x − c
L
t)]
α
= A exp
2z
H
exp
−
z
κH
exp[ik
x
(x − c
L
t)]
(14.79)
where the coefficients S, P, A are constants. This wave, known as the Lamb wave,
has no vertical velocity and propagates horizontally with the speed of sound c
L
.
Waves propagating in the horizontal direction only are known as trapped waves or
evanescent waves. As mentioned above, a wave moving with the speed of sound is
important in numerical weather prediction since it places a severe restriction on the
maximum time step. For details on Lamb waves see Haltiner and Williams (1980).
14.7 Lee waves
When air is forced to cross a mountain ridge under statically stable conditions,
individual air parcels are displaced from their equilibrium level. In this case the air
parcels begin to oscillate about their equilibrium positions. The consequence is the
formation of a wave system in the lee region of the mountain. There exists a rather
detailed theory for two-dimensional air flow crossing idealized mountains; see, for
example, Queney (1948), Queney et al. (1960), and Smith (1979). The interested
reader may consult Gossard and Hooke (1975), where this topic is treated in some
detail. More realistic simulations are possible with the help of numerical models,
which may be verified by means of satellite observations.
14.8 Propagation of energy
Wave motion is associated with the transport of physical quantities such as energy
and momentum. In this section we will briefly derive an important equation for
the transport of energy by gravity and acoustic waves. To keep the analysis simple
but still sufficiently instructive, we will restrict our discussion to frictionless wave
motion in the (x, z)-plane. Furthermore, we consider a scale of motion on which
Coriolis effects are not important. We refer to Gossard and Hooke (1975) and
Pichler (1997), where additional details may be found.
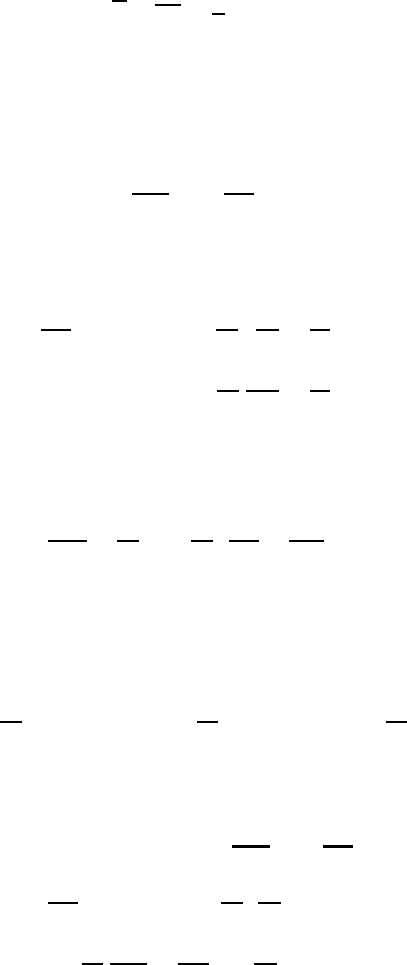
14.8 Propagation of energy 419
If p
,u
,w
are the perturbed field quantities due to wave motion, we must
average the energy flux F = i
1
F
x
+ i
3
F
z
(energy per unit area and time) over one
complete cycle τ , yielding
F = pv =
1
τ
τ
0
pv dt (14.80)
In order to assume solutions of the type (14.35), we must have a constant-coefficient
system of differential equations. To handle this particular problem, we transform
the sytem (14.31) as shown next. First we set δ = 1 and introduce the operator
d
1
/dt.Thisgives
d
1
u
dt
+ α
0
∂p
∂x
= 0(14.81a)
Next we apply the operator d/dt to (14.31b) and eliminate dα
/dt by means of
(14.31c), yielding
d
2
1
dt
2
+ ω
2
Br
w
+ α
0
d
1
dt
∂
∂z
+
g
c
2
L
p
= 0
with ω
2
Br
= g
1
α
0
∂α
0
∂z
−
g
c
2
L
(14.81b)
Here we have written the Brunt–Vaisala frequency ω
Br
as defined in (14.56) in a
more suitable form. Finally, we combine (14.31c) and (14.31d) and obtain
d
1
p
dt
−
g
α
0
w
+
c
2
L
α
0
∂u
∂x
+
∂w
∂z
= 0(14.81c)
The wave solution (14.35) cannot be applied to (14.81) since α
0
depends on
height. In order to obtain a constant-coefficient system, we transform the variables
according to
u
= U
α
0
α
s
1/2
,w
= W
α
0
α
s
1/2
,p
= P
α
0
α
s
1/2
(14.82)
where α
s
is a constant. Refer to Bretherton (1966). This transformation leads to the
system
d
1
U
dt
+ α
s
∂P
∂x
= 0
d
2
1
dt
2
+ ω
2
Br
W + α
s
d
1
dt
∂
∂z
+ E
P = 0
α
s
c
2
L
d
1
P
dt
+
∂U
∂x
+
∂
∂z
− E
W = 0
(14.83)
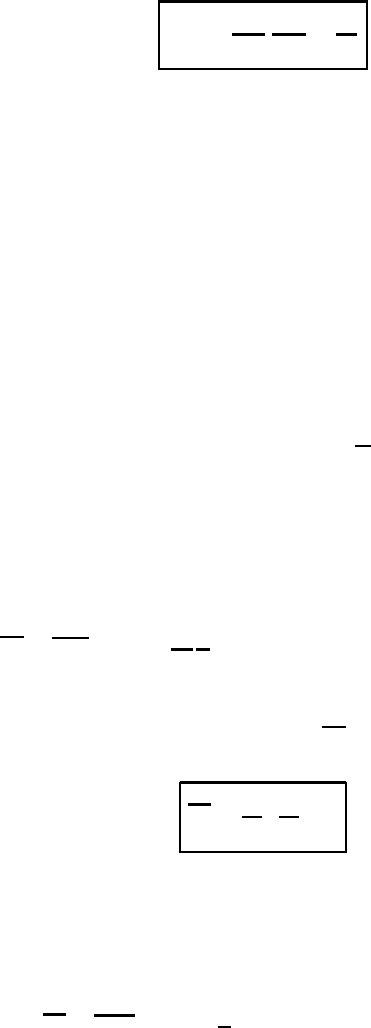
420 Wave motion in the atmosphere
Here we have introduced the so-called Eckart coefficient
E =−
1
2α
0
∂α
0
∂z
+
g
c
2
L
(14.84)
Assuming that we have a basic isothermal state, equation (14.83) is a constant-
coefficient system so that the trial solution
U
W
P
=
A
1
A
2
A
3
exp[i(k
x
x + k
z
z − ωt)] (14.85)
may be applied. The coefficients A
i
are constant amplitudes. The resulting
equations
(a) χA
1
− α
s
k
x
A
3
= 0
(b)
ω
2
Br
− χ
2
A
2
+ α
s
χ(k
z
− iE)A
3
= 0
(c) k
x
A
1
+ (k
z
+ iE)A
2
−
α
s
c
2
L
χA
3
= 0
with χ = ω − k
x
u
0
(14.86)
give the relations among the various A
i
which are needed in order to find F
x
and F
z
.
Employing (14.80), we obtain
F
x
= p
u
= A
1
A
3
α
0
α
s
1
τ
τ
0
cos
2
(k
x
x + k
z
z − ωt) dt (14.87)
since only the real part of the wave is physically meaningful. By eliminating A
1
from this equation, we find that the energy flux F
x
is proportional to the square of
the pressure amplitude:
F
x
=
α
s
2
k
x
χ
A
2
3
(14.88)
In order to find the correlation F
z
= p
w
we proceed likewise. Inspection shows
that equation (14.86b) is complex. In order to establish a relationship between p
and w
that is entirely real, we set the Eckart coefficient E equal to zero. Thus we
obtain the following relation for the energy flux in the z-direction:
F
z
= p
w
= A
2
A
3
1
τ
τ
0
cos
2
(k
x
x + k
z
z − ωt) dt (14.89)
