Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


14.2 The group velocity 401
In passing we would like to remark that the functions cos(kr −ωt) have constant
values on a sphere of radius r at a given time. As t increases the functions would
represent spherically expanding waves except for the fact that they are not solutions
of the wave equation. However, it is easy to verify that the function U (r, t ) =
(1/r)cos(kr − ωt) is a solution of the wave equation
∂
2
(Ur)
∂r
2
=
1
c
2
∂
2
(Ur)
∂t
2
(14.9)
14.2 The group velocity
In connection with the transport of energy by waves we need to discuss briefly
the concept of the group velocity. When dealing with trigonometric functions it is
often convenient to use the complex notation. Instead of (14.3) we introduce
U = U
0
exp[i(k · r − ωt)] (14.10)
It is understood that the real part is the actual physical quantity being represented.
Now let us consider two harmonic waves that have slightly different angular
frequencies ω + ω and ω − ω. The corresponding wavenumbers will, in
general, also differ. These shall be denoted by k +k and k − k. Let us assume,
in particular, that the two waves have the same amplitudes U
0
and are traveling in
the same direction, which is taken to be the z-direction. Superposition of the two
waves gives
U = U
0
exp[i(k + k)z − i(ω + ω)t] + U
0
exp[i(k − k)z − i(ω − ω)t]
(14.11a)
which can be rewritten as
U = U
0
exp[i(kz − ωt)] {exp[i(k z − ω t)] + exp[−i(k z − ω t)]}
(14.11b)
Using the Euler formula we obtain
U = 2U
0
exp[i(kz − ωt)] cos(k z − ω t)(14.11c)
This expression can be regarded as a single wave described by 2U
0
exp[i(kz−ωt)],
which has a modulation envelope cos(k z − ω t) as shown in Figure 14.3.
Generalization to three dimensions results in
U = 2U
0
exp[i(k · r − ωt)] cos(k · r − ω t)(14.11d)
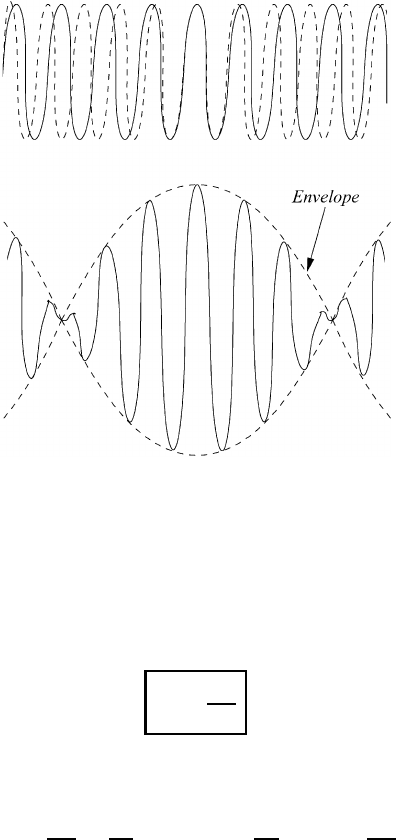
402 Wave motion in the atmosphere
Fig. 14.3 The env
elope of the combination
of two harmonic waves.
where now 2U
0
exp[i(k · r − ωt)] is the single wave and cos(k · r − ω t)the
modulation envelope. Inspection of (14.11c) shows that the modulation amplitude
does not travel with the phase velocity ω/k but at the rate c
gr
= ω/k,whichis
called the group velocity. In the limit c
gr
is given by
c
gr
=
dω
dk
(14.12)
Utilizing (14.8) we find
c
gr
=
dω
dk
=
d
dk
(kc) = c + k
dc
dk
= c − L
dc
dL
(14.13)
showing that the group velocity differs from the phase velocity only if the phase
velocity c explicitly depends on the wavelength. Rossby waves, these are large-scale
synoptic waves, to be discussed later, exhibit this behavior. The dependency of the
angular frequency on the wavenumber, that is ω = ω(k), is known as the dispersion
relation. Whenever dc/dL > 0 one speaks of normal dispersion;ifdc/dL < 0
the dispersion is called anomalous dispersion. Very informative discussions on
wave motion and group velocity can be found in many textbooks on optics and
elsewhere. We refer to Fowles (1968).

14.3 Perturbation theory 403
The generalization of the group velocity to three dimensions is carried out by
expanding the total derivative dω as
dω =
∂ω
∂k
x
dk
x
+
∂ω
∂k
y
dk
y
+
∂ω
∂k
z
dk
z
=∇
k
ω · dk
with ∇
k
ω =
∂ω
∂k
x
i
1
+
∂ω
∂k
y
i
2
+
∂ω
∂k
z
i
3
(14.14)
Defining the components of the group velocity vector c
gr
as
c
gr,x
=
∂ω
∂k
x
,c
gr,y
=
∂ω
∂k
y
,c
gr,z
=
∂ω
∂k
z
(14.15a)
we obtain
c
gr
=∇
k
ω (14.15b)
14.3 Perturbation theory
In order to isolate some simple wave forms we need to linearize the basic
atmospheric equations by means of the so-called perturbation method.Thesetof
equations to be linearized consists of the three equations representing frictionless
motion on the tangential plane,
du
dt
=
∂u
∂t
+ u
∂u
∂x
+ v
∂u
∂y
+ w
∂u
∂z
=−α
∂p
∂x
+ fv
dv
dt
=
∂v
∂t
+ u
∂v
∂x
+ v
∂v
∂y
+ w
∂v
∂z
=−α
∂p
∂y
− fu
dw
dt
=
∂w
∂t
+ u
∂w
∂x
+ v
∂w
∂y
+ w
∂w
∂z
=−α
∂p
∂z
− g
(14.16)
the continuity equation,
α
∂u
∂x
+
∂v
∂y
+
∂w
∂z
−
∂α
∂t
+ u
∂α
∂x
+ v
∂α
∂y
+ w
∂α
∂z
= 0(14.17)
and the first law of thermodynamics, which will be approximated by assuming that
we are dealing with adiabatic processes:
de + pdα = 0(14.18)
Here, α =1/ρ is the specific volume. Since we are going to investigate the behavior
of dry air only, we do not need to consider the equations for partial concentrations.

404 Wave motion in the atmosphere
Treating the air as an ideal gas, we may substitute the ideal-gas law and the
differential for the internal energy
pα = R
0
T, de = c
v,0
dT (14.19)
into (14.18) to obtain, after some slight rearrangements,
pκ
∂α
∂t
+ u
∂α
∂x
+ v
∂α
∂y
+ w
∂α
∂z
+ α
∂p
∂t
+ u
∂p
∂x
+ v
∂p
∂y
+ w
∂p
∂z
= 0
(14.20)
with R
0
= c
p,0
− c
v,0
and κ = c
p,0
/c
v,0
.
We will now summarize the perturbation method.
(i) Any variable ψ is decomposed into a part repre
senting the basic state
ψ
0
and another
part describing the disturbance ψ
, which is also called the perturbation:
ψ = ψ
0
+ ψ
(14.21)
(ii) The basic state ψ
0
is considered known and must satisfy the o
riginal system of non-
linear equations.
(iii) The total motion, i.e. the basic field plus the disturbance, must satisfy the system of
nonlinear equations.
(iv) The perturbations ψ
are assumed to be very small in comparison with the basic
state ψ
0
.
(v) Products of perturbations are ignored. This implies the linearization.
On applying (14.21) to the variables of motion and to the thermodynamic vari-
ables we find
(u, v, w, p, α, T ) = (u
0
,v
0
,w
0
,p
0
,α
0
,T
0
) + (u
,v
,w
,p
,α
,T
)(14.22)
As an example we demonstrate the perturbation procedure by linearizing a
simplified form of the advection equation:
∂u
∂t
+ u
∂u
∂x
= 0(14.23)
We split u according to (14.22) and obtain
∂
∂t
(u
0
+ u
) + (u
0
+ u
)
∂
∂x
(u
0
+ u
) = 0(14.24a)
Owing to assumption (ii) we may write
∂u
0
∂t
+ u
0
∂u
0
∂x
= 0(14.24b)

14.3 Perturbation theory 405
By subtracting (14.24b) from (14.24a) we obtain the linearized equation
∂u
∂t
+ u
∂u
0
∂x
+ u
0
∂u
∂x
= 0(14.24c)
from which, according to (v), the nonlinear term u
∂u
/∂x has been omitted. In this
very simple case the linearization procedure is very brief. For the more complex
equations of the complete atmospheric system this procedure is very tedious, so a
shortcut method would be welcome.
Such a method is the so-called Bjerkness linearization procedure, which results
directly in the linearized equations. Suppose that we wish to linearize the product
ab. This is done by varying the factor a to give
δa = a
and then multiplying a
by the basic state factor b
0
. This is followed by obtaining another product term by
multiplying the basic state a
0
by the variation δb = b
of the factor b.Inprinciple
this is the product rule of differential calculus, which may be written as
δ(ab) = (ab)
= (δa)b
0
+ a
0
δb = a
b
0
+ a
0
b
(14.25a)
Suppose that we wish to linearize the triple products abc occurring in (14.20).
This is best done by combining two factors to give d = bc and then using the rule
(14.25a):
δ(abc) = δ(ad) = (δa)d
0
+ a
0
δd = a
b
0
c
0
+ a
0
(b
c
0
+ b
0
c
)(14.25b)
Application of the Bjerkness linearization rule results in the following system of
atmospheric equations, which can be checked quickly and easily for accuracy. The
equations of atmospheric motion are given by
∂u
∂t
=−u
∂u
0
∂x
− v
∂u
0
∂y
− w
∂u
0
∂z
− u
0
∂u
∂x
− v
0
∂u
∂y
− w
0
∂u
∂z
− α
∂p
0
∂x
− α
0
∂p
∂x
+ fv
∂v
∂t
=−u
∂v
0
∂x
− v
∂v
0
∂y
− w
∂v
0
∂z
− u
0
∂v
∂x
− v
0
∂v
∂y
− w
0
∂v
∂z
− α
∂p
0
∂y
− α
0
∂p
∂y
− fu
∂w
∂t
=−u
∂w
0
∂x
− v
∂w
0
∂y
− w
∂w
0
∂z
− u
0
∂w
∂x
− v
0
∂w
∂y
− w
0
∂w
∂z
− α
∂p
0
∂z
− α
0
∂p
∂z
(14.26)
406 Wave motion in the atmosphere
The adiabatic equation is
p
κ
∂α
0
∂t
+ u
0
∂α
0
∂x
+ v
0
∂α
0
∂y
+ w
0
∂α
0
∂z
+ α
∂p
0
∂t
+ u
0
∂p
0
∂x
+ v
0
∂p
0
∂y
+ w
0
∂p
0
∂z
+ p
0
κ
∂α
∂t
+ u
∂α
0
∂x
+ v
∂α
0
∂y
+ w
∂α
0
∂z
+ u
0
∂α
∂x
+ v
0
∂α
∂y
+ w
0
∂α
∂z
+ α
0
∂p
∂t
+ u
∂p
0
∂x
+ v
∂p
0
∂y
+ w
∂p
0
∂z
+ u
0
∂p
∂x
+ v
0
∂p
∂y
+ w
0
∂p
∂z
= 0
(14.27)
which is easily identified by the appearance of the factor κ = c
p,0
/c
v,0
.The
continuity equation is given by
α
∂u
0
∂x
+
∂v
0
∂y
+
∂w
0
∂z
+ α
0
∂u
∂x
+
∂v
∂y
+
∂w
∂z
−
∂α
∂t
+ u
∂α
0
∂x
+ v
∂α
0
∂y
+ w
∂α
0
∂z
+ u
0
∂α
∂x
+ v
0
∂α
∂y
+ w
0
∂α
∂z
= 0
(14.28)
Finally the linearized ideal-gas law is given by
p
α
0
+ p
0
α
= R
0
T
(14.29)
In order to isolate certain types of wave motion we are going to use trial solutions
of the type
U = U
0
exp[i(k
x
x + k
y
y + k
z
z − ωt)] (14.30)
In order to make the system of linearized equations (14.26)–(14.29) more
manageable, it is customary to introduce some simplifications without disturbing
the basic physics contained in the original set of linearized equations. These
simplifications are the following.
(i) We restrict the propagation of plane waves to the (x,z)-plane: v = 0,∂/∂y = 0.
(ii) We assume that there is a constant basic c
urrent given by
u
0
= constant so that
v
0
= w
0
= 0 and hence v
= 0.
(iii) We assume that, in the basic state, the atmosphere is in hydrostatic balance:
α
0
∂p
0
/∂z =−g.
(iv) W
e assume that isothermal conditions pertain for the basic
field so
that
∂α
0
/∂z = g/p
0
.
(v) We assume that the rotation of the earth may be ignored by setting f = 0.
(vi) The basic thermodynamic variables are taken to be independent of x and t.
14.4 Pure sound waves 407
Application of these assumptions results in the following simplified set of
linearized equations:
(a)
∂u
∂t
+ u
0
∂u
∂x
+ α
0
∂p
∂x
= 0
(b) δ
∂w
∂t
+ u
0
∂w
∂x
+ α
0
∂p
∂z
− g
α
α
0
= 0
(c) α
0
∂p
∂t
+ u
0
∂p
∂x
− gw
+ p
0
κ
∂α
∂t
+ u
0
∂α
∂x
+ w
∂α
0
∂z
= 0
(d) α
0
∂u
∂x
+
∂w
∂z
−
∂α
∂t
+ u
0
∂α
∂x
+ w
∂α
0
∂z
= 0
(14.31)
Following Haltiner and Williams (1980), we have introduced the quantity δ into the
equation for vertical motion. If δ = 1 this equation remains unchanged; by setting
δ = 0 we ignore certain vertical-acceleration terms.
We shall now transform (14.31) by introducing the relative pressure q = p
/p
0
and the relative density s = ρ
/ρ
0
=−α
/α
0
. The latter relation may be easily
obtained by linearizing the equation ρα = 1. Using the abbreviation d
1
/dt =
∂/∂t + u
0
∂/∂x and matrix notation, we find without difficulty
d
1
dt
0 R
0
T
0
∂
∂x
0
0 δ
d
1
dt
R
0
T
0
∂
∂z
− gg
0
g(κ − 1)
R
0
T
0
d
1
dt
−κ
d
1
dt
∂
∂x
∂
∂z
−
g
R
0
T
0
0
d
1
dt
u
w
q
s
= 0(14.32)
Inspection shows that all coefficients multiplying the variables (u
,w
,q,s)orthe
differential operators are constants, so the operator method may be applied to solve
the homogeneous system of differential equations (14.32). We will demonstrate
the procedure in the following sections.
14.4 Pure sound waves
The system (14.32) contains sound waves and gravity waves, including interactions
between these two types of wave. In order to isolate pure sound waves we have

408 Wave motion in the atmosphere
to set g = 0. In the general case we set δ = 1. Nonzero values of the unknown
functions (u
,w
,q,s) of the homogeneous system can be obtained by setting the
determinant of the four-by-four matrix in (14.32) equal to zero:
d
1
dt
0 R
0
T
0
∂
∂x
0
0
d
1
dt
R
0
T
0
∂
∂z
0
00
d
1
dt
−κ
d
1
dt
∂
∂x
∂
∂z
0
d
1
dt
= 0(14.33)
The evaluation of the determinant gives the partial differential equations
∂
∂t
+ u
0
∂
∂x
2
∂
∂t
+ u
0
∂
∂x
2
− κR
0
T
0
∂
2
∂x
2
+
∂
2
∂z
2
ψ
j
(x,z, t) = 0
(14.34)
which applies to the four variables (ψ
1
,ψ
2
,ψ
3
,ψ
4
) = (u
,w
,q,s). Since we are
dealing with a constant-coefficient system we may assume the validity of wave
solutions of the type
ψ
j
= A
j
exp
i(k
x
x + k
z
z − ωt)
(14.35)
where the A
j
are constant coefficients. The system (14.31) is linear so that any
linear combination of solutions is a solution also. Therefore, it is sufficient for
our purposes to consider a single harmonic. Substituting (14.35) into (14.34) and
rearranging the result gives the fourth degree frequency equation
(k
x
u
0
− ω)
2
[−(k
x
u
0
− ω)
2
+ k
2
κR
0
T
0
] = 0 with k
2
= k
2
x
+ k
2
z
(14.36)
in agreement with Haltiner and Williams (1980), who assumed that α
0
= constant
and p
0
= constant.
We will now discuss the four roots of this equation. The quadratic first factor
results in
ω
1,2
= 2πν
1,2
= k
x
u
0
=
2π
L
x
u
0
(14.37a)
From this equation it follows that the phase speed
c
x
=
k
x
k
u
0
(14.37b)
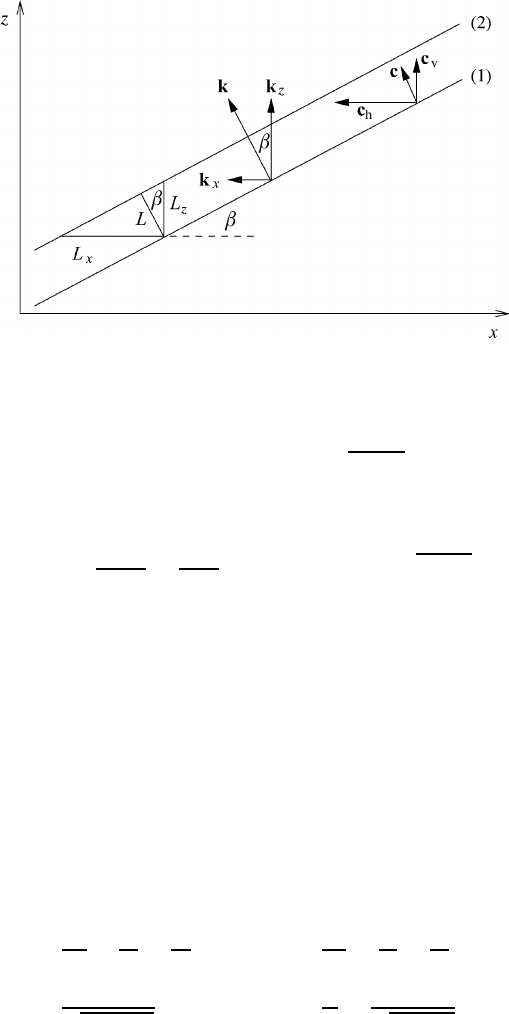
14.4 Pure sound waves 409
Fig. 14.4 Propagation of plane harmonic waves in the (x,z)-plane.
corresponds to simple advection. The third and fourth roots are given by
ω
3,4
= 2πν
3,4
= k
x
u
0
± k
κR
0
T
0
(14.37c)
The corresponding phase velocities are
c
3,4
= ν
3,4
L =
ω
3,4
L
2π
=
k
x
u
0
k
± c
L
with c
L
=
κR
0
T
0
(14.37d)
It is seen that c
3,4
consists of two parts including the basic current u
0
and the
Laplace speed of sound c
L
which is independent of direction and amounts to about
330 m s
−1
.
With the help of Figure 14.4 we are going to investigate the propagation of plane
harmonic waves in the (x,z)-plane. The wave vector k is normal to the equiphase
surfaces (phase lines k
x
x + k
z
z = constant in the (x,z)-plane). The wavelength L
is the normal distance between two of these surfaces, (1) and (2); the distances L
x
and L
z
are the distances between these two surfaces in the x-andz-directions. The
displacement of equiphase surfaces occurs with the phase speed c. The horizontal
and vertical displacement speeds are denoted by c
h
and c
v
. From the trigonometric
relations we find
sin β =
L
L
x
=
c
c
h
=
k
x
k
, cos β =
L
L
z
=
c
c
v
=
k
z
k
L =
L
x
L
z
L
2
x
+ L
2
z
,c=
ω
k
=
ω
k
2
x
+ k
2
z
(14.38)
If the phase speed c and β are given, we can calculate c
h
. From Figure 14.4 it can
be seen that the horizontal speed c
h
increases with decreasing angle β.
410 Wave motion in the atmosphere
14.5 Sound waves and gravity waves
Gravity waves arise from the differential effects of gravity on air parcels of different
densities at the same level. It might be a better terminology to call them buoyancy
waves. Let us reconsider the linearized system (14.32). For simplicity, without
changing the essential physics, we set the basic flow speed u
0
= 0sothatd
1
/dt
degenerates to the partial derivative ∂/∂t. The determinant of the four-by-four
matrix of (14.32) now reduces to
∂
∂t
0 R
0
T
0
∂
∂x
0
0 δ
∂
∂t
R
0
T
0
∂
∂z
− gg
0
g(κ − 1)
R
0
T
0
∂
∂t
−κ
∂
∂t
∂
∂x
∂
∂z
−
g
R
0
T
0
0
∂
∂t
= 0(14.39)
whose expansion is
δ
∂
4
∂t
4
− κR
0
T
0
δ
∂
4
∂x
2
∂t
2
+
∂
4
∂z
2
∂t
2
+ κg
∂
3
∂z∂t
2
− g
2
(κ − 1)
∂
2
∂x
2
ψ
j
= 0
(14.40)
Here (ψ
1
,ψ
2
,ψ
3
,ψ
4
) = (u
,w
,q,s). With the exception of one term all space
derivatives in (14.40) are of second order. This asymmetry can be removed by
substituting
ψ
j
= exp
gz
2R
0
T
0
F
j
(x,z, t)(14.41)
into (14.40) to obtain
δ
∂
4
∂t
4
− κR
0
T
0
δ
∂
4
∂x
2
∂t
2
+
∂
4
∂z
2
∂t
2
+
κg
2
4R
0
T
0
∂
2
∂t
2
− g
2
(κ − 1)
∂
2
∂x
2
F
j
= 0
(14.42)
where all space derivatives are now of second order. Substitution of the constant-
coefficient harmonic-wave solution
F
j
= A
j
exp[i(k
x
x + k
z
z − ωt)] (14.43)
into (14.42) results in the frequency equation
δω
4
− ω
2
κR
0
T
0
δk
2
x
+ k
2
z
+
κg
2
4R
0
T
0
+ g
2
(κ − 1)k
2
x
= 0(14.44)
