Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


13.9 The composite Ekman layer 381
A few critical remarks on the solution (13.122) will be helpful. As stated above,
the cross-isobar angle α = 45
◦
is too large to be in reasonable agreement with
observations, for which α generally varies from 15
◦
to 25
◦
. The reason for this
is that the exchange coefficient was assumed to be constant with height whereas
in reality it varies rapidly with height in the lower 10–20 m, as we know from
Prandtl-layer theory and from Figure 13.6. Therefore, the solution (13.122) should
not be extended to the ground but only to some height above the ground that is often
taken as the height of the anemometer level. We know from Prandtl-layer theory
that, in the surface layer, the wind shear is along the wind vector itself. Using this
as a lower boundary condition, and if z = 0 denotes the height of a well-exposed
anemometer, we obtain a more realistic solution for the Ekman spiral. The cross-
isobar angle then is not fixed at the unrealistically high value of 45
◦
but is smaller.
The solution to the problem is given, for example, in Petterssen (1956). We will not
discuss this situation, but we present another solution that is based on the piecewise
linear distribution of the exchange coefficient as shown in Figure 13.6. The price
we have to pay for the more realistic approximation of the exchange coefficient is
a more complicated analytic solution.
13.9 The composite Ekman layer
As stated above, there are many numerical solutions with which to model the
atmospheric boundary layer. We will now show that it is also possible to obtain an
analytic solution for the wind profile by subdividing the Ekman layer into different
sections, in each of which sections K varies linearly with height. This treatment
allows the exchange coefficient to vary with height in a reasonable manner. The
right-hand side of equation (13.115) is now given by
∇·(
J + R) = ρ
∂
∂z
K
∂
v
h
∂z
(13.129)
Instead of (13.118) we have to solve the system
d
K
du
dz
dz
=−fv,
d
K
dv
dz
dz
= f (u − u
g
)(13.130)
Proceeding as before, these differential equations will be combined to give a single
equation:
K
d
2
dz
2
(u + iv − u
g
) +
dK
dz
d
dz
(u + iv − u
g
) − if (u + iv − u
g
) = 0(13.131)

382 The atmospheric boundary layer
Introducing the abbreviation g =u + iv − u
g
wemayalsowrite
K
d
2
g
dz
2
+
dK
dz
dg
dz
− if g = 0(13.132)
Comparison with (13.119) shows that now an additional term appears.
In the following we will derive the solution for the case that the Ekman layer is
subdivided into three parts as shown in Figure 13.6. In the central section of the
vertical profile of the exchange coefficient the classical Ekman solution applies.
For the upper section z>h
2
and the lower section z
Pr
<z<h
1
the linear
approximations of the exchange coefficient K are given by
z
Pr
≤ z ≤ h
1
: K
1
= b
1
+ a
1
(z − z
Pr
) > 0 with a
1
=
K
max
− b
1
h
1
− z
Pr
h
2
≤ z ≤
H: K
2
= b
2
+ a
2
(
H − z) > 0witha
2
=
K
max
− b
2
H − h
2
(13.133)
where we have admitted a residual value b
2
at the top of the boundary layer.
In order to transform (13.132) into a Bessel-type differential equation for which
the solution is known, we have to introduce suitable transformation variables. Let us
first direct our attention to the lower section, transforming the exchange coefficient
K
1
as
K
1
=
b
1
+ a
1
(z − z
Pr
) = ξ>0(13.134)
The transformations
dξ
dz
=
a
1
2ξ
,
d
2
ξ
dz
2
=−
a
2
1
4ξ
3
dg
dz
=
dg
dξ
dξ
dz
,
d
2
g
dz
2
=
d
2
ξ
dz
2
dg
dξ
+
dξ
dz
2
d
2
g
dξ
2
(13.135)
follow from the differentiation rules, so (13.132) may be written as
d
2
g
dξ
2
+
1
ξ
dg
dξ
−
4if g
a
2
1
= 0(13.136)
The solution to this equation is given in various textbooks on differential equations.
We refer to Magnus and Oberhettinger (1948), where a very general form of Bessel’s
equation and its solution are given. These two equations are
d
2
u
dz
2
+ (2α − 2νβ + 1)
1
z
du
dz
+
β
2
γ
2
z
2β−2
+
α(α − 2βν)
z
2
u = 0
u = z
βν−α
Z
ν
γz
β
(13.137)

13.9 The composite Ekman layer 383
The symbol Z stands for the cylinder function. In our situation we have α = 0,β=
1,ν= 0, and γ
2
=−4if /a
2
1
, so the solution function is of zeroth order and is
given by
g
l
= Z
0
l
l
i
3/2
ξ
with l
l
=
2
√
f
a
1
(13.138)
where l
l
is a constant applying to the lower section. The complete solution can be
constructed from any pair of independent particular solutions. The form
g
l
= c
l
J
0
l
l
i
3/2
ξ
+ d
l
K
0
l
l
i
1/2
ξ
(13.139)
where J
0
is a Bessel function of the first kind and K
0
a modified Bessel function
of the second kind is suitable for our purposes. As before, the subscript l on the
integration constants c and d refers to the lower section. Since the argument of the
Bessel functions is complex, it is customary to introduce the form
g
l
= c
l
[ber
0
(l
l
ξ) + i bei
0
(l
l
ξ)] + d
l
[ker
0
(l
l
ξ) + i kei
0
(l
l
ξ)]
(13.140)
where ber
0
(x), bei
0
(x), ker
0
(x), and kei
0
(x) are the Kelvin functions referring to
the real and imaginary parts of the Bessel functions J
0
and K
0
, respectively.
1
The
function ber
0
(x) +i bei
0
(x) is finite at the origin but becomes infinite as x becomes
infinite. ker
0
(x)+i kei
0
(x) is infinite at the origin but approaches zero as x becomes
infinite. An excellent introductory discussion on Bessel functions is given in Wylie
(1966).
We now turn to the transformation and the solution of (13.132) in the upper
section. We apply the transformation
K
2
=
b
2
+ a
2
(
H − z) = η>0(13.141)
From the differentiations
dη
dz
=−
a
2
2η
,
d
2
η
dz
2
=−
a
2
2
4η
3
(13.142)
there follows the differential equation
d
2
g
dη
2
+
1
η
dg
dη
−
4if g
a
2
2
= 0(13.143)
From (13.137) with α = 0,β= 1,ν= 0, and γ
2
=−4if /a
2
2
we find the solution
g
u
= Z
0
l
u
i
3/2
η
with l
u
=
2
√
f
a
2
(13.144)
1
Many textbooks omit the suffix 0 from the functions ber
0
(x), bei
0
(x), ker
0
(x), and kei
0
(x).
384 The atmospheric boundary layer
which is a cylinder function of zeroth order. The subscript u on the constant l
u
refers to the upper section. The general solution is given by
g
u
= c
u
J
0
l
u
i
3/2
η
+ d
u
K
0
l
u
i
1/2
η
(13.145)
Analogously to (13.140) we may also write
g
u
= c
u
[ber
0
(l
u
η) + i bei
0
(l
u
η)] + d
u
[ker
0
(l
u
η) + i kei
0
(l
u
η)]
(13.146)
Now we have three solutions for the composite boundary layer. For the lower
section we have the solution (13.140). For the middle layer with a constant exchange
coefficient K
max
the solution (13.120) applies. It is restated in a convenient form as
g
m
= c
m
exp(Az)[cos(Az) + i sin(Az)] + d
m
exp(−Az)[cos(Az) − i sin(Az)]
(13.147)
with A =
√
f/(2K
max
). For the upper section we have the solution (13.146). The
g
l
,g
m
,andg
u
occurring in (13.140), (13.146), and (13.147) are complex numbers,
so
u(z) =[g(z) + u
g
],v(z) =[g(z)] (13.148)
There are six constants in the composite solution to be evaluated, so six boundary
statements must be at our disposal. These will be stated next:
(i) The log–linear wind profile (13.73) must hold within the Prandtl layer. We require
that, at the top of the Prandtl layer z
Pr
, the derivatives of the log–linear wind profile
and of the solution for the lower section coincide.
(ii) At the top of the Ekman layer the wind becomes geostrophic.
(iii) The wind components at the interfaces h
1
and h
2
are continuous.
(iv) The derivatives of the wind components are continuous at these interfaces.
The continuity of the derivatives of wind components eliminates kinks in the
wind profile. This is the same thing as requiring that the stresses are continuous at
the interfaces. The composite-boundary-layer problem has the undesirable feature
that the derivatives dK/dz are discontinuous at the interfaces.
The derivatives of the solution functions appearing in (13.140) and (13.146) are
d ber
0
(x)
dx
=
1
√
2
[ber
1
(x) + bei
1
(x)],
d bei
0
(x)
dx
=
1
√
2
[−ber
1
(x) + bei
1
(x)]
d ker
0
(x)
dx
=
1
√
2
[ker
1
(x) + kei
1
(x)],
d kei
0
(x)
dx
=
1
√
2
[−ker
1
(x) + kei
1
(x)]
(13.149)
13.9 The composite Ekman layer 385
Application of these equations to the lower and upper sections leads to
x = l
l
ξ = l
l
b
1
+ a
1
(z − z
Pr
),
dx
dz
=
l
l
a
1
2ξ
,
d
dz
=
dx
dz
d
dx
d
dz
ber
0
(x)
bei
0
(x)
ker
0
(x)
kei
0
(x)
l
=
l
l
a
1
2
√
2ξ
ber
1
(x) + bei
1
(x)
− ber
1
(x) + bei
1
(x)
ker
1
(x) + kei
1
(x)
− ker
1
(x) + kei
1
(x)
(13.150a)
and
x = l
u
η = l
u
b
2
+ a
2
(
H − z),
dx
dz
=−
l
u
a
2
2η
,
d
dz
=
dx
dz
d
dx
d
dz
ber
0
(x)
bei
0
(x)
ker
0
(x)
kei
0
(x)
u
=−
l
u
a
2
2
√
2η
ber
1
(x) + bei
1
(x)
− ber
1
(x) + bei
1
(x)
ker
1
(x) + kei
1
(x)
− ker
1
(x) + kei
1
(x)
(13.150b)
The functions ber
0
(x), bei
0
(x), ker
0
(x), kei
0
(x), ber
1
(x), bei
1
(x), kei
1
(x), and
ker
1
(x) are tabulated, for example, in the Handbook of Mathematical Functions by
Abramowitz and Segun (1968).
In order to evaluate the six integration constants it is best to introduce a compact
notation. All parts appearing in (13.140), (13.146), and (13.147) are abbreviated as
A
z
= ber
0
[l
l
ξ(z)],B
z
= bei
0
[l
l
ξ(z)],C
z
= ker
0
[l
l
ξ(z)]
D
z
= kei
0
[l
l
ξ(z)],E
z
= ber
0
[l
u
η(z)],F
z
= bei
0
[l
u
η(z)]
G
z
= ker
0
[l
u
η(z)],H
z
= kei
0
[l
u
η(z)],I
z
= exp(Az)cos(Az)
J
z
= exp(Az)sin(Az),K
z
= exp(−Az)cos(Az),L
z
=−exp(−Az)sin(Az)
(13.151)
By using this compact notation it is a simple matter to write down the six boundary
statements:
At z = z
Pr
– continuity of stresses:
u
∗
k
1
z
Pr
+
α
2L
∗
= c
l
d
dz
(A
z
+ iB
z
)
z
Pr
+ d
l
d
dz
(C
z
+ iD
z
)
z
Pr
(13.152)
At z = h
1
– continuity of velocities:
c
l
(A
z
+ iB
z
)
h
1
+ d
l
(C
z
+ iD
z
)
h
1
= c
m
(I
z
+ iJ
z
)
h
1
+ d
m
(K
z
+ iL
z
)
h
1
(13.153)

386 The atmospheric boundary layer
At z = h
2
– continuity of velocities:
u
g
+ c
u
(E
z
+ iF
z
)
h
2
+ d
u
(G
z
+ iH
z
)
h
2
= u
g
+ c
m
(I
z
+ iJ
z
)
h
2
+ d
m
(K
z
+ iL
z
)
h
2
(13.154)
At z =
H – continuity of velocities:
0 = c
u
(E
z
+ iF
z
)
H
+ d
u
(G
z
+ iH
z
)
H
(13.155)
At z = h
1
– continuity of stresses:
c
l
d
dz
(A
z
+ iB
z
)
h
1
+ d
l
d
dz
(C
z
+ iD
z
)
h
1
= c
m
d
dz
(I
z
+ iJ
z
)
h
1
+ d
m
d
dz
(K
z
+ iL
z
)
h
1
(13.156)
At z = h
2
– continuity of stresses:
c
u
d
dz
(E
z
+ iF
z
)
h
2
+ d
u
d
dz
(G
z
+ iH
z
)
h
2
= c
m
d
dz
(I
z
+ iJ
z
)
h
2
+ d
m
d
dz
(K
z
+ iL
z
)
h
2
(13.157)
These equations are sufficient to evaluate the real and imaginary parts of the
constants. Once the constants for a given distribution of the exchange coefficient
are known, we can use the various solutions to construct the wind profile.
In principle it is possible to extend the solution method by representing the
vertical profiles of the exchange coefficients by more than three linear parts. For
each additional part one obtains two more integration constants that have to be
determined by formulating additional boundary conditions analogously to those
stated above.
In order to investigate the quality of the solution for the composite Ekman layer,
numerous case studies aiming to obtain an optimal choice of the subdivision of
the exchange coefficient profile have been performed. Some examples will now
be presented. Figure 13.9 depicts the wind profiles for the classical approach
(curve 2) and three different solutions of the composite Ekman layer (curves
3–5) corresponding to an approximation of the exchange-coefficient profile by
three, four, and five linear sections. Moreover, the results are compared with a
numerical solution resulting from the O’Brien exchange coefficient (curve 1) which
is treated here as the reference case. The upper left-hand panel shows the vertical
distributions of the exchange coefficient. The vertical profiles of the horizontal
wind components are depicted in the other two panels. The geostrophic wind was
chosen as (u
g
,v
g
) = (10, 0) m s
−1
.
From all case studies the following conclusions are drawn.
(i) The composite solutions yield a distinct improvement over the
classical Ekman solu-
tion. The three-section solution is already sufficient to obtain a substantial improve-
ment. An additional refinement of the exchange-coefficient profile to four or five
sublayers has no great effect.
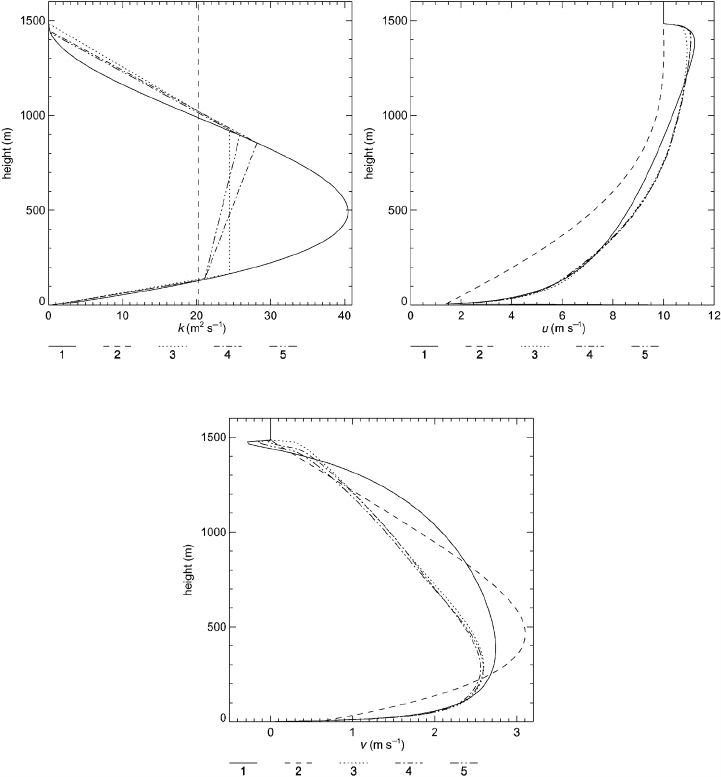
13.9 The composite Ekman layer 387
Fig. 13.9 Vertical profiles of the exchange coefficient and of the components of the
horizontal wind. Curve 1: the profile according to O’Brien (1970); curve 2: the classical
soluti
on; curves 3, 4, and 5: composite solutions with t
hree, four, and
five linear
sections.
(ii) Increasing the resolution of the composite profiles in the middle region of the boundary
layer has only a minor influence on the results.
(iii) A rough estimate of the maximum value of the exchange coefficient is sufficient to
construct the composite profiles since the results are barely affected by the particular
choice of this value.
(iv) The undershooting of the v-component at the top of the boundary layer is obtained
only if the resolution of the exchange-coefficient profile is fine enough there.
(v) The cross-isobar angle assumes reasonable values.

388 The atmospheric boundary layer
The analytic solution can also be used to check the accuracy of other approx-
imate methods for obtaining the vertical wind profile in the boundary layer. The
mathematical development of this section is based on our own unpublished lecture
notes.
13.10 Ekman pumping
We conclude this chapter by studying in a very approximate manner the interaction
of the atmospheric boundary layer with the free atmosphere; see Figure 13.1. From
Figure 13.7 we recognize that the horizontal wind vector below the geostrophic-
wind height has a component pointing from high to low pressure. This deviation is
responsible for a mass transport perpendicular to the isobars, resulting in an equal-
ization of the large-scale pressure field. It is well known from synoptic observations
that the large-scale geostrophic wind is horizontally not uniform. The task ahead is
to investigate the influence of the horizontal variation of the geostrophic wind on
the Ekman layer. As before, to keep things simple, we assume that the geostrophic
wind is directed to the east so that v
g
= 0. The geostrophic-wind component u
g
,
however, varies in the northerly direction so that u
g
= u
g
(y). Furthermore, we
assume that the exchange coefficient K and the Coriolis parameter f do not vary
in space. From the classical Ekman solution (13.122) we find the wind variation in
the northerly direction to be given by
∂u
∂y
=
∂u
g
∂y
1 − exp(−Az)cos(Az)
,
∂v
∂y
=
∂u
g
∂y
exp(−Az)sin(Az)
(13.158)
Since u does not vary in the easterly direction the continuity equation for an
incompressible fluid reduces to
∂v
∂y
+
∂w
∂z
= 0(13.159)
Height integration gives the vertical wind component at the geostrophic-wind
height:
w(z
g
) =−
z
g
0
∂u
g
∂y
exp(−Az)sin(Az) dz (13.160)
with w(z = 0) = 0. Hence, the variation of the wind component v in the northerly
direction induces a vertical wind. Assuming barotropic conditions so that the
geostrophic wind u
g
is height-independent, we can carry out the integration without

13.10 Ekman pumping 389
difficulty. The result is
w(z
g
) =−
∂u
g
∂y
1 + exp(−π )
2A
= ζ
g
√
K
with ζ
g
=−
∂u
g
∂y
,
√
K
=
1 + exp(−π )
2A
≈
K
2f
(13.161)
where use of (13.121) was made. In this equation the geostrophic vorticity ζ
g
has
been introduced. The sign of w(z
g
) is controlled by the sign of the geostrophic
vorticity. For cyclonic circulations ζ
g
> 0sothatw(z
g
) > 0; for anticyclonic cir-
culations ζ
g
< 0sothatw(z
g
) < 0. For typical large-scale systems the geostrophic
vorticity is about 10
−5
s
−1
. Assuming a value of K = 5−10 m
2
s
−1
and a midlat-
itude Coriolis parameter f = 10
−4
s
−1
, we find that the vertical velocity amounts
to a few tenths of a centimeter per second. Certainly, such small vertical veloc-
ities cannot be measured. Nevertheless, these small values of w are sufficient to
influence significantly the life times of synoptic systems.
According to (13.161) the vertical motion induced by boundary-layer friction
causes a large-scale vertical motion leading to the breakdown of high-pressure
systems while low-pressure systems are filling up. Thus the large-scale pressure
gradient becomes very small so that the geostrophic wind and the geostrophic vor-
ticity cease to exist. It takes large-scale processes to create new pressure gradients.
Let us estimate how long it takes, for example, to fill up a cyclonic system.
Instead of computing the change in pressure we may just as well compute the
change with time of the geostrophic vorticity. We start with a simplified form of
the barotropic vorticity equation (10.146):
dη
g
dt
=
d
dt
(ζ
g
+ f ) =−η
g
∇
h
·
v
h
= η
g
∂w
∂z
≈ f
∂w
∂z
(13.162)
since usually ζ
g
f . Ignoring the spatial variation of the Coriolis parameter, we
find
dζ
g
dt
= f
∂w
∂z
(13.163)
This expression will be integrated with respect to height from the top of the
boundary layer z
g
to the top of the atmosphere z
T
, yielding
z
T
z
g
dζ
g
dt
dz = f
w(z
T
) − w(z
g
)
(13.164)
Assuming that the geostrophic wind is independent of height even above z
g
,the
geostrophic vorticity is height-independent also, so (13.164) can be integrated
directly, yielding
(z
T
− z
g
)
dζ
g
dt
= f
w(z
T
) − w(z
g
)
(13.165)
390 The atmospheric boundary layer
The vertical velocity vanishes at the top of the atmosphere and z
T
− z
g
is about z
T
.
Therefore, we find
dζ
g
dt
=−
ζ
g
z
T
Kf
2
(13.166)
where we have replaced w(z
g
) with the help of (13.161). This differential equation
can be solved immediately to give
ζ
g
(t) = ζ
g
(0) exp
−
Kf
2z
2
T
t
(13.167)
showing that the vorticity is decreasing exponentially in time. The reason for this is
the existence of the ageostrophic wind component which resulted from the turbulent
viscosity of the air. This behavior of the atmosphere is called Ekman pumping.
Let us estimate the time it takes for the vorticity to decrease to 1/e of its original
value. Obviously this relaxation time t
e
can be estimated from
t
e
=
2z
2
T
Kf
(13.168)
Using z
T
= 10
4
m, K = 10 m
2
s
−1
,andf = 10
−4
s
−1
we find that t
e
amounts
to about four days. It takes about nine days for the geostrophic vorticity to decay
to 10% of its original value, which is in rough agreement with the life time of a
low-pressure system.
Finally, let us recall that no frictional effects were included in the simplified
vorticity equation (13.162). Therefore, the frictional effect observed within the
Ekman layer on low- and high-pressure systems is indirect. On retracing the steps
leading to (13.161) we find that a vertical circulation above the Ekman layer was
induced due to the divergence of the ageostrophic wind component. By means
of the divergence term on the right-hand side of the vorticity equation we finally
obtained (13.166), showing that the vorticity is decreasing with time due to the
turbulent viscosity of the air. This indirect frictional effect on the synoptic systems
is known as the spin down and t
e
is the spin-down time.
Etling (1996) continued this discussion by posing the question of whether the
residual turbulent viscosity existing in the free atmosphere is sufficient to stop the
circulation in low- and high-pressure systems. He drew the conclusion that the effect
of the turbulent viscosity in the free atmosphere plays an unimportant role in the
dynamics of synoptic systems. The 10% of the entire atmospheric mass contained
in the atmospheric boundary layer is mainly responsible for the destruction of the
atmospheric pressure systems.
