Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

13.2 Prandtl-layer theory 351
to investigate the formation and dissipation of ground fog, the Prandtl-layer theory
must be relaxed and radiative processes are then of paramount importance.
13.2.1 The modified budget equations
We are now ready to state the budget equations in their modified forms as they
apply to the Prandtl layer.
13.2.1.1 The continuity equation
Owing to stationarity and horizontal homogeneity, the continuity equation (11.35a)
reduces to
D
ρ
Dt
=
∂
∂z
(
ρw) = 0orρw = constant (13.2)
It is customary to treat ρ as a constant. Since w(z
0
) = 0 we find within the Prandtl
layer
w(z) = 0(13.3)
so that the velocity divergence vanishes:
∇·(
ρ
v) = i
3
·
∂
∂z
(
ρ
v
h
) = 0, ∇·
v = 0(13.4)
As a consequence of these equations and due to the stationarity, the averaged budget
operator and the individual time derivative also vanish:
D
Dt
(ρψ) = 0,
dψ
dt
= 0(13.5)
13.2.1.2 The continuity equation for the concentrations
The continuity equation for the concentration of water vapor (11.35b) reduces to
the divergence expression
∇·
J
1
+J
1
t
=
∂
∂z
i
3
·
J
1
+J
1
t
= 0 =⇒ i
3
·
J
1
+J
1
t
=
J
1
+J
1
t
= constant
(13.6)
From the requirement of horizontal homogeneity it follows immediately that the
sum of the vertical components of the diffusive water-vapor fluxes is constant with
height. The diffusion fluxes for dry air can be directly obtained from
J
0
+ J
0
t
=−
J
1
+ J
1
t
(13.7)
352 The atmospheric boundary layer
13.2.1.3 The equation of motion
From (11.35d), together with the various hypothetical Prandtl-layer statements, we
immediately obtain
i
3
∂p
∂z
− i
3
·
∂
∂z
(
J + R) =−i
3
ρg (13.8)
since ∇
h
φ = 0andi
3
∂φ/∂z = i
3
g. We will now define the stress vector of the
boundary layer as
T = i
3
· (J + R)(13.9)
Next, we require some information on the turbulence state of the Prandtl layer. We
assume that we have horizontal isotropy of turbulence as discussed in Section 11.8.
From (11.92) it follows that
T =
ρK
v
v
∂
v
h
∂z
(13.10)
This is a horizontally directed vector that is parallel to ∂
v
h
/∂z. Equation (13.8)
now splits into a horizontal and a vertical part:
∂p
∂z
=−
ρg,
∂T
∂z
= 0 =⇒ T = constant
(13.11)
The first equation is the hydrostatic equation for the averaged pressure and den-
sity. From the second equation it follows that the stress vector is constant with
height within the Prandtl layer. Direct application of the hypothetical Prandtl-
layer conditions to the kinetic-energy equation of mean motion (11.45) also yields
T = constant.
Since the horizontal velocity vanishes at z
0
, the stress vector must also be
parallel to the velocity vector itself. This is most easily seen by writing the vertical
derivative as a finite difference. Since T,∂
v
h
/∂z,and
v
h
all have the same direction,
it is of advantage to rotate the coordinate system about the z-axis so that one of the
horizontal axes is pointing in the direction of the three vectors. It is customary to
select the x-axis so that we may write
|
v
h
|
=u, v = 0,
|
T
|
= τ =
ρK
v
v
∂u
∂z
,
∂τ
∂z
= 0, T ·
∂
v
h
∂z
= τ
∂u
∂z
(13.12)
The vertical distribution of τ is shown in Figure 13.1.
13.2 Prandtl-layer theory 353
13.2.1.4 The budget equation of the turbulent kinetic energy
We will now direct our attention to the budget of the turbulent kinetic energy
as stated in (11.46). The budget operator vanishes according to (13.5). Owing to
horizontal homogeneity the divergence part degenerates to
∇·
k
t
− v
· J
=
∂E
∂z
with E = i
3
·
k
t
− v
· J
, k
t
= ρv
v
2
2
(13.13)
The double scalar product on the right-hand side of (11.46) may be rewritten as
∇
v··
J + R
= i
3
∂
v
h
∂z
··
J + R
= i
3
·
J + R
·
∂
v
h
∂z
= T ·
∂
v
h
∂z
(13.14)
since J and R are symmetric tensors. The power term v
·∇p appearing in (11.46)
will be replaced by (11.70) with the approximation J
θ
· A = 0. Utilizing R
0
ρ/p =
1/
T , the term multiplying the heat flux J
θ
t
in (11.70) is approximated as
∇ ln
=
∂ ln
∂z
i
3
=−
g
c
p,0
T
i
3
(13.15)
Here and in the following c
p
will be approximated by c
p,0
. With these approxima-
tions the budget of the turbulent kinetic energy can finally be written as
∂E
∂z
= T ·
∂
v
h
∂z
−
− J
θ
t
·∇ln
= τ
∂u
∂z
−
+ J
θ
t
g
c
p,0
T
(13.16)
with
= J··∇v ≥ 0
13.2.1.5 The budget equation of the internal energy
Application of the hypothetical Prandtl-layer conditions to (11.48) gives the first
version of the budget equation for the internal energy
∂
∂z
J
h
+ J
h
t
=−J
θ
t
g
c
p,0
T
+ (13.17)
Next we introduce the sensible enthalpy fluxes
J
h
s
= J
h
− J
n
h
n
,J
h
s,t
= J
h
t
− J
n
t
h
n
(13.18)
Utilizing the latter equation, the vertical component of the vector relation (11.69)
can be written as
J
h
t
= J
θ
t
+ J
t
+ J
n
t
h
n
(13.19)

354 The atmospheric boundary layer
In the absence of ice we may write for the atmospheric system J
n
t
h
n
= J
0
t
h
0
+
J
1
t
h
1
+ J
2
t
h
2
. An analogous expression holds also for J
n
h
n
. The enthalpies
h
k
depend on temperature, and, for the condensed phase, even on pressure. As we
have seen, the Prandtl-layer theory is based on numerous hypothetical conditions.
Thus we feel justified in applying the additional assumption that the
h
k
may be
treated as constants. Since the definition of any thermodynamic potential includes
an arbitrary constant that is at our disposal, we set
h
0
= 0and
h
2
= 0. Thus the
latent heat l
21
=
h
1
−
h
2
=
h
1
is a constant also and we may write
J
n
h
n
= l
21
J
1
,J
n
t
h
n
= l
21
J
1
t
(13.20)
Instead of (13.17) we obtain for the budget equation for the internal energy
∂
∂z
J
h
+ J
h
t
=
∂
∂z
J
h
s
+ J
θ
t
+ J
t
+
J
n
+ J
n
t
h
n
=−J
θ
t
g
c
p,0
T
+ (13.21)
Owing to (13.6) and (13.20) we may write
(
J
n
+ J
n
t
)
h
n
=
J
1
+ J
1
t
l
21
,
∂
∂z
J
1
+ J
1
t
l
21
= 0(13.22)
According to (13.1e) the heat flux J
θ
t
is constant with height so that (13.21) finally
reduces to
∂
∂z
J
h
s
+ J
t
=−J
θ
t
g
c
p,0
T
+
(13.23)
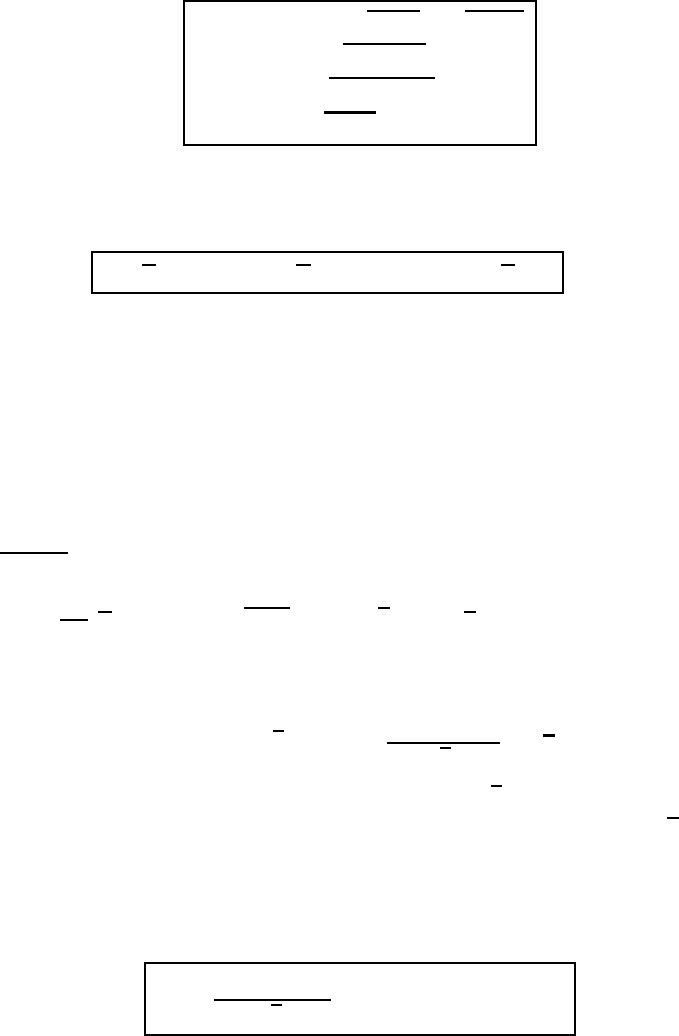
It is customary to introduce the following abbreviating symbols:
W =
J
h
s
+ J
t
Heat flux: H = J
θ
t
with
∂H
∂z
= 0
Moisture flux: Q =
J
1
+ J
1
t
with
∂Q
∂z
= 0
(13.24)
No special name is given to W . Utilizing these definitions the energy budget of the
Prandtl layer is summarized as
Kinetic energy
v
2
2
: −
∂
∂z
(τu) =−τ
∂u
∂z
Turbulent kinetic energy
k:
∂E
∂z
= τ
∂u
∂z
−
+
gH
c
p,0
T
Internal energy e:
∂W
∂z
=
−
gH
c
p,0
T
(13.25)
13.2 Prandtl-layer theory 355
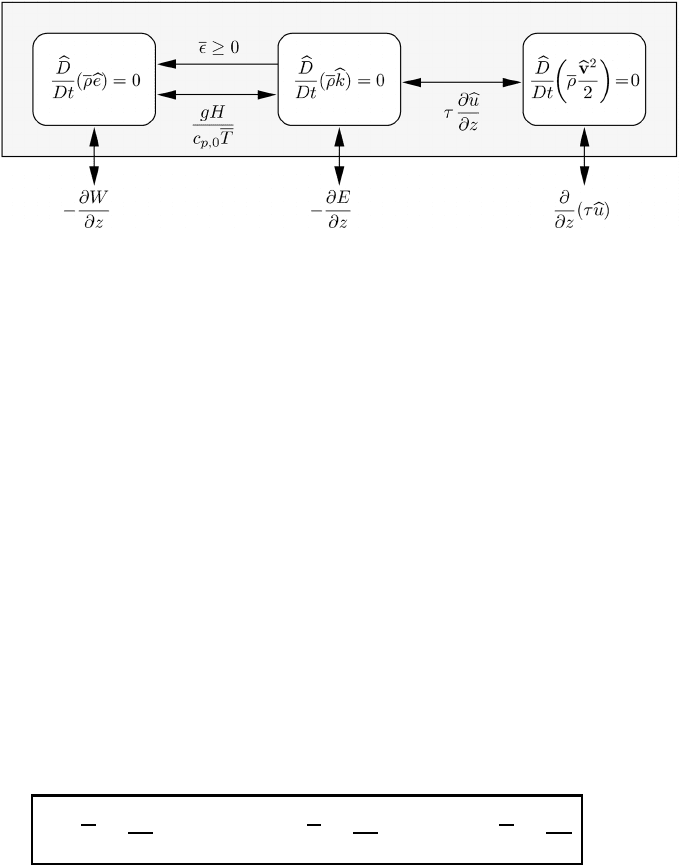
Fig. 13.2 The energy balance within the Prandtl layer.
The budget equation of the kinetic energy of mean motion follows directly from
(13.11) where we have shown that T = constant. As required, the sum of the
sources, i.e. the sum of all right-hand-side terms, equals zero. The energy budget
can be usefully displayed graphically as shown in Figure 13.2. We think of a
spatially fixed unit volume V . The three boxes within V represent changes with
time per unit volume of the mean values of the internal energy, the turbulent kinetic
energy, and the kinetic energy of the mean motion. The mean change in total energy
contained in V is given by the sum of the three boxes. The arrows piercing the outer
line marking V denote the interaction with the outside world, i.e. with neighboring
boxes. The arrows connecting the energy boxes represent energy transformations
within V . With one exception all internal transformations may go in two directions.
Only the dissipation of energy is positive definite and can go in one direction only,
from the turbulent kinetic energy to the internal energy.
Now we are going to give explicit expressions for H and Q. Scalar multiplication
of (11.88a) by i
3
gives the desired relation for H . We assume that Q may be
expressed analogously. Together with the corresponding equation (13.12) for τ ,we
obtain the phenomenological equations of the Prandtl layer as
τ = ρK
v
∂u
∂z
,H=−c
p,0
ρK
θ
∂
θ
∂z
,Q=−ρK
q
∂q
∂z
(13.26)
where we have suppressed the subscript v in the exchange coefficients since in
the Prandtl layer only vertical fluxes exist. Furthermore, we have introduced the
variable q = m
1
usually denoting the specific humidity in the system of moist air.
While H directly follows from (11.88a), the quantity Q is only an approximation,
as can be seen from (11.88c) and (11.86).
It is a well-known fact that the turbulent fluxes exceed the corresponding molec-
ular fluxes by several orders of magnitude. Therefore, it is customary to ignore
the molecular fluxes since these are always added to the corresponding turbulent
356 The atmospheric boundary layer
fluxes. Ignoring the molecular fluxes, however, is not a necessity. If the molecular
fluxes are totally ignored the turbulent fluxes are given by
T = i
3
· R =−i
3
· ρv
v
=−ρw
v
H = i
3
· J
θ
t
=
ρc
p,0
θw
W = i
3
· J
t
= ρc
p,0
w
θ
≈ 0
Q = i
3
· J
1
t
= ρw
q
(13.27)
as follows from (11.36), (11.38), and (11.65).
In boundary-layer theory it is customary to introduce the scaling variables u
∗
,
T
∗
,andq
∗
by means of the defining equations
τ = ρu
2
∗
,H=−ρc
p,0
u
∗
T
∗
,Q=−ρu
∗
q
∗
(13.28)
The quantity u
∗
has the dimension of a velocity and is therefore known as the
frictional velocity.ThevariableT
∗
has the dimension of temperature while q
∗
is
dimensionless. If these scaling variables are known then τ , H ,andQ may be
determined since the density of the Prandtl layer is considered known also.
13.2.2 The Richardson number
Let us rewrite the complete budget equation for the turbulent kinetic energy (11.46)
without using the specific Prandtl-layer conditions. Substituting from (11.70) for
v
·∇p and ignoring the term involving the pressure fluctuations, we find
D
Dt
ρ
k
+∇·(k
t
− v
· J) =∇
v··(J + R) − − J
θ
t
·∇ln
(13.29)
The right-hand side then represents the source for the turbulent kinetic energy,
which can be written in the form
Q
k
=∇
v··(J + R)
1 −
J
θ
t
·∇ln
∇
v··(J + R)
− (13.30)
Without proof we accept that the frictional term ∇
v ··(
J + R) is positive definite
so that it permanently produces kinetic energy. While the energy dissipation
≥ 0
permanently transforms
k into internal energy, see Figure 13.2, the third term on
the right-hand side of (13.29) can have either sign, thus producing or destroying
turbulent kinetic energy. We will investigate the situation more closely. The fraction
on the right-hand side of (13.30) is called the flux Richardson number:
Ri
f
=
J
θ
t
·∇ln
∇
v ··(J + R)
=
<1 production of
k
>1 destruction of
k
(13.31)
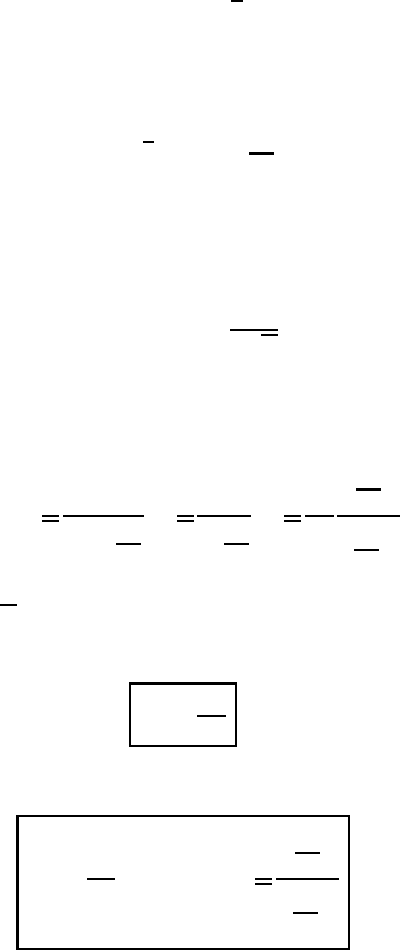
13.2 Prandtl-layer theory 357
Ignoring for the moment the contribution of in (13.30), we see that turbulent
kinetic energy is produced if Ri
f
< 1; otherwise dissipation takes place.
Let us now employ the Prandtl-layer assumptions. According to (13.12) and
(13.14) the denominator of (13.31) reduces to
∇
v··(
J + R) = τ
∂u
∂z
(13.32)
Observing that the exchange coefficient is a positive quantity, we easily recognize
with the help of (13.12) that the denominator of the flux Richardson number cannot
be negative. From (13.15) we obtain for the numerator of (13.31)
J
θ
t
·∇ln
=−
gH
c
p,0
T
(13.33)
Therefore, applying (13.26) and (13.28), the flux Richardson number may be
expressed as
Ri
f
=−
g
T
H
c
p,0
τ
∂u
∂z
=
g
T
T
∗
u
∗
∂u
∂z
=
g
T
K
θ
K
v
∂
θ
∂z
∂u
∂z
2
(13.34)
In the Prandtl layer
T may also be replaced by
θ. It is customary to introduce the
turbulent Prandtl number as the ratio of the two exchange coefficients:
Pr =
K
v
K
θ
(13.35)
so that the flux Richardson number can also be written as
Ri
f
=
Ri
Pr
with Ri =
g
T
∂
θ
∂z
∂u
∂z
2
(13.36)
The variable Ri is known as the gradient Richardson number or simply the Richard-
son number, which was introduced in the previous chapter, see equation (12.77).
Inspection of (13.34) clearly indicates that the numerator is a measure for the pro-
duction or suppression of buoyancy energy. The denominator represents the part of
the turbulence that is mechanically induced by shear forces of the basic air current.
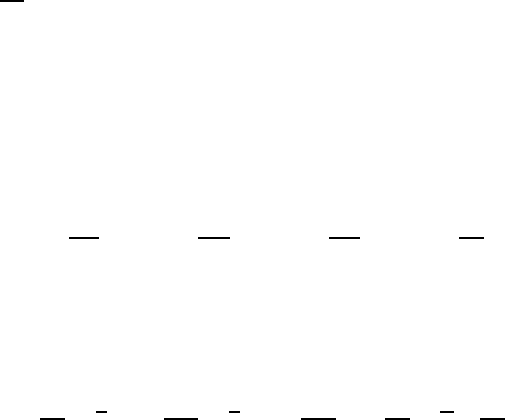
358 The atmospheric boundary layer
For statically unstable air the gradient of the potential temperature is negative, so
Ri
f
< 0. This causes an increase of turbulence. In a statically stable atmosphere the
gradient of the potential temperature is positive so that Ri
f
> 0. If ∂
θ/∂z is large
enough this results in a sizable reduction of turbulent kinetic energy. If the flux
Richardson number becomes larger than one, the first term on the right-hand side
of (13.30) changes sign. The flux Richardson number Ri
f
= 1 is considered to be
an upper limit of the so-called critical flux Richardson number Ri
f,c
. Some modern
theoretical work on the basis of detailed observations indicates that the critical flux
Richardson number should be close to 0.25. However, this value is still uncertain.
For flux Richardson numbers larger than this value the transition from turbulent to
laminar flow takes place. The flux Richardson number will be fundamental to the
discussion of stability in the next few sections.
13.3 The Monin–Obukhov similarity theory of the neutral Prandtl layer
Before deriving various relationships for the non-neutral or diabatic Prandtl layer
we will summarize some conditions and relations pertaining to neutral stratifi-
cation. The relationships for the neutral Prandtl layer will then be generalized to
accommodate arbitrary stratifications. In case that the Prandtl layer is characterized
by static neutral stratification we may write
∂
θ
∂z
= 0,T
∗
= 0,J
θ
t
= H = 0 =⇒ Ri
f
= Ri = 0(13.37)
As stated in equations (13.12) and (13.24) the stress τ , the heat flux H ,andthe
moisture flux Q do not change with height within the Prandtl layer. For reasons
of symmetry we will also assume that the quantity E as defined in (13.13) will be
constant with height so that we have
∂E
∂z
= 0,
∂H
∂z
= 0,
∂Q
∂z
= 0,
∂τ
∂z
= 0(13.38)
Using the conditions stated in (13.37) and (13.38), the budget equations for the
turbulent kinetic and internal energy (13.25) reduce to
τ
∂u
∂z
=
,
∂W
∂z
=
=⇒
∂W
∂z
= τ
∂u
∂z
=
ρu
2
∗
∂u
∂z
(13.39)
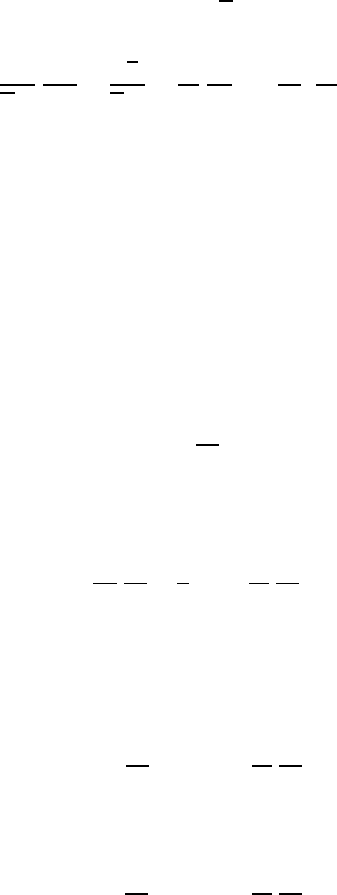
13.3 The Monin–Obukhov similarity theory of the neutral Prandtl layer 359
On multiplying this equation by the factor z/(ρu
3
∗
) we obtain
z
ρu
3
∗
∂W
∂z
=
z
ρu
3
∗
=
z
u
∗
∂u
∂z
= z
∂
∂z
u
u
∗
(13.40)
This equation will be the starting point for some of the analysis to follow.
The reader unfamiliar with the fundamental ideas of similarity theory is invited to
consult Appendix A to this chapter. There the Buckingham theorem is introduced,
where is a dimensionless number. This theory is a useful tool in many branches
of science. The Monin–Obukhov (MO) similarity hypothesis (Monin and Obukhov,
1954) consists of two essential parts.
(i) In the neutral Prandtl layer there exists a unique relation among the height z,the
frictional velocity u
∗
, and the vertical velocity gradient ∂u/∂z:
F
1
z, u
∗
,
∂u
∂z
= 0(13.41)
From dimensional analysis it can be shown that there exists a
dimensionless number
so that we have
=
z
u
∗
∂u
∂z
=
1
k
or
kz
u
∗
∂u
∂z
= 1(13.42)
The universal constant k = 0.4istheVon Karman constant. Details are given in
Appendix A, Example 1.
(ii) In analogy to (13.41) we assume that corresponding statements are true for the temper-
ature distribution:
F
2
z, T
∗
,
∂
θ
∂z
= 0,
kz
T
∗
∂
θ
∂z
= 1(13.43)
and for the moisture distribution:
F
3
z, q
∗
,
∂q
∂z
= 0,
kz
q
∗
∂q
∂z
= 1(13.44)
Equation (13.43) must be viewed as a limit statement since both T
∗
and ∂
θ/∂z are zero
in the neutral Prandtl layer. Equations (13.43) and (13.44) will not be needed at present
but will be used later.
A number of interesting and important conclusions may be drawn from the MO
similarity theory.
360 The atmospheric boundary layer
13.3.1 The functions u, ,andW
From (13.40) and (13.42) it follows immediately that
kz
ρu
3
∗
∂W
∂z
=
kz
u
∗
∂u
∂z
= kz
∂
∂z
u
u
∗
= 1(13.45)
Integration of the last equation of (13.45) gives the well-known logarithmic wind
profile:
u(z) =
u
∗
k
ln
z
z
0
, u(z = z
0
) = 0,z≥ z
0
(13.46)
At the roughness height z
0
the wind speed vanishes. There exist extensive tables in
which values of the estimated roughness height are given. For example, for short
grass z
0
is in the range 0.01–0.04 m, whereas for long grass z
0
= 0.10 m might be
an acceptable value.
Similarly we find expressions for W :
W (z) − W (z
0
) =
ρu
3
∗
k
ln
z
z
0
,z≥ z
0
(13.47)
so that the dissipation of energy
from (13.39) is given by
(z) =
ρu
3
∗
kz
,z≥ z
0
(13.48)
We need to point out that the Prandtl-layer theory does not permit the evaluation
of W (z
0
).
13.3.2 The phenomenological coefficient K
v
We are now ready to obtain an expression for the exchange coefficient K
v
for the
neutral Prandtl layer. From (13.26) and (13.28) we obtain
K
v
=
u
2
∗
∂u/∂z
,z≥ z
0
(13.49)
which is valid for the diabatic and for the neutral Prandtl layer. Utilizing (13.45)
we immediately find for the neutral Prandtl layer
K
v
= kzu
∗
,z≥ z
0
(13.50)
showing that, within the neutral Prandtl layer, the exchange coefficient increases
linearly with height. This is the assumption we have made in Section 12.6.
