Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.


12.6 A prognostic equation for the exchange coefficient 341
We have implicitly assumed that the k
−5/3
law holds for the entire range k
≥ k;
the error we make thereby is likely to be small. Now we solve (12.55) for "
M
and
obtain
"
M
= ak
k
3/2
with a =
3κ
K
2
−3/2
(12.56)
Substituting this expression into (12.53) gives
K = bk
−1
k
1/2
with b =
3
4
2
3
−1/2
κ
H
(12.57)
Now we have obtained the desired relations among
"
M
,
k,andK. Finally, the
wavenumber k will be replaced by a characteristic length l by means of
k =
2π
L
=
1
l
(12.58)
From (12.57), using the definition (12.58), it follows that
k =
K
bl
2
(12.59a)
so that (12.56) can be written as
"
M
=
a
l
K
bl
3
=
aK
3
b
3
l
4
(12.59b)
By combining (12.59b) with (12.56) and (12.57), we obtain
K = ab
k
2
"
M
(12.60)
Hence, it is seen that the exchange coefficient itself is proportional to the square of
the turbulent kinetic energy and inversely proportional to the dissipation of energy
"
M
. We are going to consider the Heisenberg exchange coefficient as a typical
exchange coefficient that is valid not only for the turbulent momentum flux but
also for the transport of other turbulent fluxes. In the next chapter we will refine
this concept.
12.6 A prognostic equation for the exchange coefficient
Before continuing our discussion, we wish to briefly elucidate the action of the
turbulent flux
v
ρψ. As an example, let us consider a simple one-dimensional
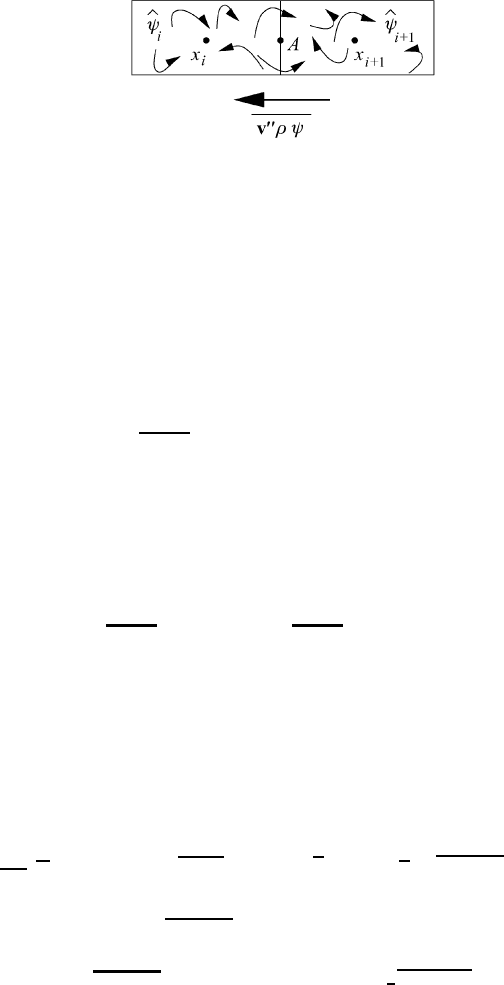
342 An excursion into spectral turbulence theory
Fig. 12.7 A schematic view of the action of a turbulent flux.
numerical grid as it may be used for the evaluation of the atmospheric equations.
The process of turbulent mixing is shown schematically in Figure 12.7. At each
central grid point x
i
the value of a physical quantity
ψ
i
represents an average for the
entire grid cell. These central values are thought to be known without discussing
how they are obtained. Within each of these cells we expect irregular turbulent
motion to take place. In order to obtain information about the turbulent flux at
point A between two grid cells x
i
and x
i+1
, we do not need (and usually cannot
obtain) information about each individual eddy or fluctuation. It is sufficient to
know the average value v
ρψ. For definiteness let us assume that the value of
ψ
increases from left to right so that
ψ
i+1
>
ψ
i
. The turbulent eddies perform a
completely disordered or stochastic motion, but each of these will be associated
with a particular value of ψ. From experience we know that, on average, a directed
transport of the quantity ψ will take place from higher toward lower ψ values. For
the turbulent flux we may therefore write
v
ρψ ∼−∇
ψ, v
ρψ =−ρK ∇
ψ (12.61)
The proportionality factor is the exchange coefficient K, which depends on the
turbulent kinetic energy of the system.
With these ideas in mind, we are ready to obtain a prognostic equation for the ex-
change coefficient K. The starting point for the derivation is the prognostic equation
(11.46) for the turbulent kinetic energy, which is repeated here for convenience:
D
Dt
(
ρ
k) +∇·(k
t
− v
· J) =∇
v··(J + R) − " − v
·∇p (12.62)
In this equation we replace
v
·∇p by a simplified form of (11.70):
v
·∇p = J
θ
t
·∇ln
, k
t
=
1
2
v
ρ(v
)
2
(12.63)
For reference the definition of the turbulent kinetic energy flux k
t
,see
equation (11.42), is included as part of this equation. By replacing the turbu-
lent kinetic energy
k in terms of the exchange coefficient K according to (12.59a)
12.6 A prognostic equation for the exchange coefficient 343
and " by (12.59b), we obtain a prognostic equation for the exchange coefficient:
D
Dt
ρ
K
bl
2
+∇·(k
t
− v
· J) =∇
v··(J + R) − J
θ
t
· ln
−
ρa
b
3
l
4
K
3
(12.64)
In the final term the air density
ρ has been inserted since we divided (12.16)
by the density. In this equation
v,
ρ,and
are considered to be known quanti-
ties. The remaining variables are still unknown and must be replaced by suitable
parameterizations.
The entire analysis of this chapter is based on the assumption that the atmosphere
is characterized by ρ = constant so that the velocity divergence is zero. In this case
the averaged molecular stress tensor
J can be written as
J = µ(∇
v +
v
∇)(12.65)
In analogy to this, assuming isotropic conditions, we may write for the Reynolds
stress tensor
R = ρK(∇
v +
v
∇)(12.66)
where K is the turbulent exchange coefficient. Since the turbulent exchange coef-
ficient K is much larger than the dynamic viscosity multiplied by the air density,
we may ignore the contribution of the mean molecular stress. Therefore, we pa-
rameterize the first term on the right-hand side of (12.64) as
∇
v··(
J + R) =∇
v··ρK(∇
v +
v
∇)(12.67)
We now consider the vectorial expression in the divergence term of equation
(12.64). Assuming that the second term may be ignored, we may write in analogy
to (12.61) the parameterized form
(k
t
− v
· J) =−ρK ∇
v
2
2
=−
ρK ∇
k =−ρK ∇
K
bl
2
(12.68)
The negative sign shows that the flow is from larger to smaller values of the
transported quantity. Finally, we need to parameterize the turbulent heat flux which
was defined by equation (11.88). For the isotropic case the exchange tensor may be
replaced by the scalar exchange coefficient. On the basis of the brief discussion we
have given above and from dimensional requirements, we find the parameterized
form
J
θ
t
=−ρ c
p
K ∇
θ (12.69)
While in (11.88) the two scalar coefficients K
θ
h
and K
θ
v
are used to parameterize J
θ
t
,
this simplified treatment admits only the exchange coefficient K. On substituting

344 An excursion into spectral turbulence theory
(12.67)–(12.69) into (12.64), the prognostic equation for the exchange coefficient
will be written as
D
Dt
ρ
K
bl
2
−∇·
ρK ∇
K
bl
2
=∇
v··
ρK(∇
v +
v
∇)
+
ρ c
p
K ∇
θ ·∇ln
−
ρa
b
3
l
4
K
3
(12.70)
Equation (12.70) is rather complex and its evaluation requires a great deal of
numerical effort. From this equation, however, we may derive an entire hierarchy of
simplifications, which were often applied when computer capabilities were insuffi-
cient. Numerical investigations of (12.70) have shown that, for many situations, the
tendency term may be neglected. For this case, after expanding the budget operator
and disregarding the local time derivative, we obtain
∇·
ρ
v
K
bl
2
−∇·
ρK ∇
K
bl
2
=∇
v··ρK(∇
v +
v
∇)
+
ρ c
p
K ∇
θ ·∇ln
−
ρa
b
3
l
4
K
3
(12.71)
This is a partial differential equation of the elliptic type representing a boundary
value problem. We select a rectangular parallelepiped as the integration domain,
for which it is customary to set K = 0 at the upper boundary z = H .Atthelower
boundary, assuming neutral conditions, we set K proportional to the frictional
velocity u
∗
, K = κz
0
u
∗
. The constant κ = 0.4 is known as the Von Karman
constant and z
0
is the roughness height. The precise definition of u
∗
and the
justification of this form of the exchange coefficient at the surface will be offered
in the following chapter.
The next simplification is to assume that we have horizontal homogeneity, so
that the gradient operator reduces to
∇
h
... = 0, ∇ ... = k
∂...
∂z
(12.72a)
By assuming additionally that w = 0 we obtain
v =
v
h
, from which it follows that
k ·
v
h
= 0, ∇
v··(∇
v +
v
∇) =
∂u
∂z
2
+
∂v
∂z
2
=
∂
v
h
∂z
2
(12.72b)
12.6 A prognostic equation for the exchange coefficient 345
For these conditions the stationary K equation is expressed by
∂
∂z
ρK
∂
∂z
K
bl
+
ρK
∂
v
h
∂z
2
+ ρc
p,0
K
∂
θ
∂z
∂ ln
∂z
−
ρ
a
b
3
l
4
K
3
= 0(12.73)
where we have made the highly satisfactory assumption that c
p
= c
p,0
. We will
now eliminate the Exner function
as shown next:
ln
=
R
0
c
p,0
ln p + constant =⇒
∂ ln
∂z
=
R
0
c
p,0
p
∂
p
∂z
=−
g
c
p,0
T
(12.74)
This results in the desired form
∂
∂z
ρK
∂
∂z
K
bl
+
ρK
∂
v
h
∂z
2
−
ρgK
T
∂
θ
∂z
−
ρ
a
b
3
l
4
K
3
= 0(12.75)
The final step in the hierarchy of approximations is to ignore the divergence term.
Solving for K
2
results in
K
2
=
b
3
l
4
a
∂
v
h
∂z
2
1 −
g
T
∂
θ
∂z
∂
v
h
∂z
−2
(12.76)
The fraction in the square bracket is known as the Richardson number Ri,
Ri =
g
T
∂
θ
∂z
∂
v
h
∂z
−2
(12.77)
Ri is a measure of the atmospheric stability. A detailed discussion follows in the
next chapter. Inserting Ri into (28.76) gives
K =
b
3
a
l
2
∂
v
∂z
√
1 − Ri = (l
)
2
∂
v
∂z
√
1 − Ri, Ri ≤ 1
(12.78)
showing that the exchange coefficient is a function of the wind shear and the
thermal stability of the atmosphere. We have also combined the product of the
constant
(b
3
/a) with the square of the characteristic length l
2
to give a new
characteristic length (l
)
2
. The quantity l
is some sort of mixing length, which will
be discussed more fully in the following chapter.
1
The resulting formula (12.78)
is often used as the definition of the exchange coefficient or Austausch coefficient
(the German word Austausch means exchange). The concept of the mixing length
will be discussed more fully in the following chapter.
1
For neutral conditions Blackadar postulated the following form of the mixing length: l
= kz/(1 +kz/λ),where
k =0.4 is the Von Karman constant and λ an asymptotic value for l
that is reached at great heights.

346 An excursion into spectral turbulence theory
12.7 Concluding remarks on closure procedures
There are several excellent books on boundary-layer theory dealing in great detail
with various closure schemes. A very illuminating account is given, for example,
by Stull (1989), where the reader can find an extensive bibliography on this subject
as well as many observational results. Here we can give only a few brief statements
on this topic.
There are local closure schemes and nonlocal closure schemes. The closure tech-
nique described in Section 12.6 is based on the turbulent-kinetic-energy equation.
This type of closure technique belongs to the group of local closure schemes. They
are called local since an unknown quantity at a point in space is parameterized
by values and gradients of known quantities at or near the same point. If nonlocal
closure techniques are used, the unknown quantity at one point in space is param-
eterized by using values of known quantities at many points. The idea behind this
concept is that larger eddies transport fluid over larger distances before the smaller
eddies have a chance to cause mixing. This is the so-called transilient turbulence
theory described in some detail by Stull (1989). There is a second nonlocal scheme
called spectral diffusivity theory. This theory has its origin in the spectral theory
which we have previously discussed.
Furthermore, it is customary to distinguish between first- and higher-order
closure schemes. To convey the idea of higher-order closure let us consider the
prognostic equation for the mean velocity
v; see equation (11.35d). This equation
includes the divergence of the Reynolds tensor which is essentially the double cor-
relation
v
v
of the velocity fluctuations. The idea behind this closure principle
is to derive a differential equation for v
v
. The mathematical steps involved
are not particularly difficult but rather lengthy so we will restrict ourselves to
a brief verbal description to demonstrate the principle. For simplicity, we assume
that the density ρ is a constant. By subtracting the equation of mean motion
from the molecular form of the Navier–Stokes equation, we obtain a differential
equation for the velocity fluctuation dv
/dt. On the right-hand side of this
equation, among other terms, there still appears the divergence of the Reynolds
tensor. Dyadic multiplication of dv
/dt first from the right and then from the
left gives two differential equations, i.e. (dv
/dt)v
= ··· and v
dv
/dt = ···.
Averaging these two equations and adding the results gives the desired
differential equation for the Reynolds tensor d(v
v
)/dt. Having derived this dif-
ferential equation does not complete the closure problem by any means since this
rather complex differential equation now contains the divergence of the unknown
triple correlation
v
v
v
. If we try to derive a differential equation for the triple
correlation, we end up with the appearence of a still higher unknown correlation
v
v
v
v
. In order to avoid the escalation of this problem, it is customary to

12.7 Concluding remarks on closure procedures 347
introduce closure assumptions. An extensive literature is available on this topic.
We refer to Mellor and Yamada (1974), who propose a second-order closure pa-
rameterization for v
v
v
.
Even second-order closure schemes are rather complicated. In order to avoid
such complications, quite early in the development of the boundary-layer theory,
the first-order closure scheme or K theory was introduced to handle the turbulence
problem. Suppose that we decompose the Reynolds tensor in a suitable manner.
Among other components we would obtain the correlation
v
w
=−K
∂
v
h
∂z
(12.79)
The first-order closure scheme simply requires that the mean value of the double
correlation is proportional to the vertical gradient of the horizontal mean veloc-
ity. The coefficient of proportionality is the exchange coefficient which must be
specified or predicted in some manner. The form of equation (12.79) explains why
the K theory is also called the gradient transport theory. Let us briefly return to
Section 12.6, where a differential equation for the turbulent exchange coefficient
was derived. This type of approach is more realistic than the first-order closure
scheme, in which the exchange coefficient is usually specified, but it is not as
refined as the second-order closure scheme. For this reason the approach presented
in Section 12.6 is called a 1.5-order closure scheme, of which many variants are
described in the literature.
Among other approaches to solving the turbulence problems, so-called
large-eddy simulation (LES) is becoming more prominent as electronic computers
become increasingly more powerful. The concept of LES is based on the idea
that some filter operation, for example averaging, is applied to the equations
of the turbulent atmosphere to separate the large and small scales of turbulent
flow. The form of the atmospheric equations modeling the flow remains
unchanged, with the turbulent-stress term replacing the molecular-viscosity term.
For this method the numerical grid is chosen fine enough to resolve the larger
eddies containing the bulk of the turbulent energy. All the information regarding
the small unresolved scales is extracted from a subgrid model. The larger
resolved eddies are sensitive to the geometry of the flow and the thermal
stratification. The much-less-sensitive unresolved small-scale eddies can be
efficiently parameterized by a relatively simple first-order closure scheme. This type
of approach has successfully been applied to a variety of turbulent-flow problems.
Comprehensive reviews have been given by Rodi (1993) and by Mason (1999),
for example.

348 An excursion into spectral turbulence theory
12.8 Problems
12.1: In order to better understand the transition from (12.18b) to (12.20), perform
simplified summations. Consider the special case that the vectors m and q are
scalars. Perform the summation (m + q)V (m)V (q)exp(m + q) with m, q =
1, 2,..., 5 and factor out the sum multiplying exp(6). Compare your result with
the sum 6V (m)V (6 − m).
12.2: Show explicitly that the transfer function W (k, k
,t) is antisymmetric.
12.3: Verify that α and β of equation (12.38a) are given by α =−
3
2
and β =
1
2
.
13
The atmospheric boundary layer
13.1 Introduction
The vertical structure of the atmospheric boundary layer is depicted in Figure 13.1.
The lowest atmospheric layer is known as the laminar sublayer and has a thickness
of only a few millimeters. It is difficult to verify the existence of this layer because
of its small vertical extent. Within the laminar sublayer all physical processes such
as the transport of momentum and heat are regulated by molecular motion. In
most boundary layer models the existence of this layer is not explicitly treated. It
stands to reason that there also exists some type of a transitional layer between
the laminar sublayer and the so-called Prandtl layer where turbulence is fully
developed.
The lower boundary of the Prandtl or surface layer is the roughness height z
0
where the mean wind is assumed to vanish. The vertical extent of the Prandtl layer
is regulated by the thermal stratification of the air and may vary from about 20 to
100 m. In this layer all turbulent fluxes are approximately constant with height. The
influence of the Coriolis force may be ignored this close to the earth’s surface, so
the turning of the wind within the Prandtl layer may be ignored. The wind speed,
however, increases very strongly in this layer, reaching a value of more than half
the wind speed at the top of the boundary layer.
Above the Prandtl layer we find the so-called Ekman layer, reaching a height
exceeding 1000 m depending on the stability of the air. Turbulent fluxes in this
layer decrease to zero at the top of the Ekman layer. Above the Ekman layer the
air flow is more or less nonturbulent. The influence of the Coriolis force in this
layer causes the turning of the wind vector. For this reason the Ekman layer is often
called the spiral layer since the nomogram of the wind vector is a spiral. The entire
region from the earth’s surface to the top of the Ekman layer is called the planetary
boundary layer.
349

350 The atmospheric boundary layer
Fig. 13.1 Subdivision of the planetary boundary layer, showing the vertical distribution
of the horizontal wind
v
h
and the stress τ within the boundary layer.
13.2 Prandtl-layer theory
It is customary to use the Cartesian coordinate system to discuss the Prandtl-layer
theory. To begin with we will summarize the hypothetical Prandtl-layer conditions:
(a)
v(z = z
0
) = 0,
v
h
(z = z
0
) = 0, w(z = z
0
) = 0
(b) Ω = 0
(c) m
2
= 0, m
3
= 0, I
2
= 0, I
3
= 0
(d) ∇·
F
R
= 0
(e) J
θ
t
= i
3
· J
θ
t
= constant
(f)
∂...
∂t
= 0, ∇
h
... = 0, ∇=i
3
∂
∂z
(13.1)
The lower boundary of this layer is the roughness height z
0
where the wind speed
vanishes, (13.1a). This condition implies a flat surface of the earth. Since the
Coriolis force is of negligible importance, we ignore this force by formally setting
the angular velocity of the earth equal to zero in the equation of motion, (13.1b).
Condensation of water vapor is not allowed to take place in the Prandtl-layer
theory, so fog does not form. This means that only dry air and water vapor are
admitted. Therefore, phase transition fluxes I
k
do not appear in the Prandtl-layer
equations, (13.1c). The divergence of the radiative flux is ignored, (13.1d). The
vertical component of the turbulent heat flux J
θ
t
does not vary with height, (13.1e).
The most essential part of the Prandtl-layer theory is the hypothesis of stationarity
and of horizontal homogeneity of all averaged variables of state, (13.1f). In order
