Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

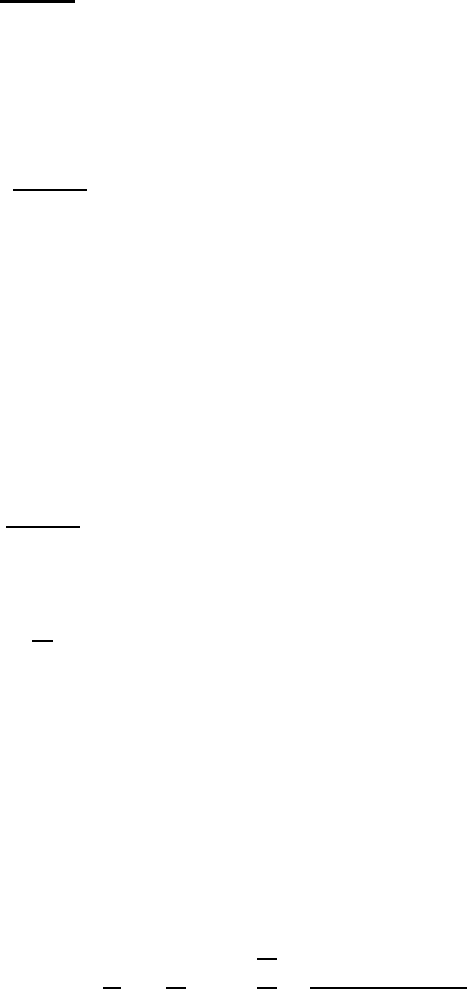
12.2 The budget equation 331
On substituting (12.10) into the equation of motion and the analogous expression
for , we obtain
∂V(n,t)
∂t
exp(in ·r) +∇·
V(m,t)V(q,t)exp(i(m + q) · r)
=−∇(n,t)exp(in · r) + ν ∇
2
V(n,t)exp(in ·r)
(12.18a)
By carrying out the differential operations involving the gradient operator and the
Laplacian, using (12.12) and (12.13), we find without difficulty the expression
∂V(n,t)
∂t
exp(in ·r) + i(m + q) · V(m,t)V(q,t)exp[i(m + q) · r]
=−i(n,t)n exp(in · r) − νn
2
V(n,t)exp(in ·r)
(12.18b)
where m, n,andq are summation vectors.
The differential equation (12.18b) must be valid for the entire range of n including
the term k. From the double sum over m and q we factor out the terms with
m + q = k or q = k − m (12.19)
The double sum over m and q now becomes a simple sum over m for each k.The
result is given by
∂V(k,t)
∂t
+ ik · V(m,t)V(k − m,t) =−i(k,t)k − νk
2
V(k,t)(12.20)
By slightly rewriting this formula we obtain
∂
∂t
+ νk
2
V(k,t) =−i(k,t)k − ik · V(m,t)V(k − m,t)(12.21)
which is the more common spectral form of the equation of motion for the complex
amplitude vector V(k,t). Summation over all m is implied. The nonlinear advection
term in the original equation of motion is the reason for the appearance of the
product of the two amplitude vectors.
12.2 The budget equation for the amplitude of the kinetic energy
First of all we generalize the expression (12.7) which is the u-component of the
kinetic energy. The average value of the total kinetic energy is then given by
1
V
V
0
v
2
2
dV
=
v
2
2
=
V(n,t) · V(−n,t)
2
= E(t)(12.22)
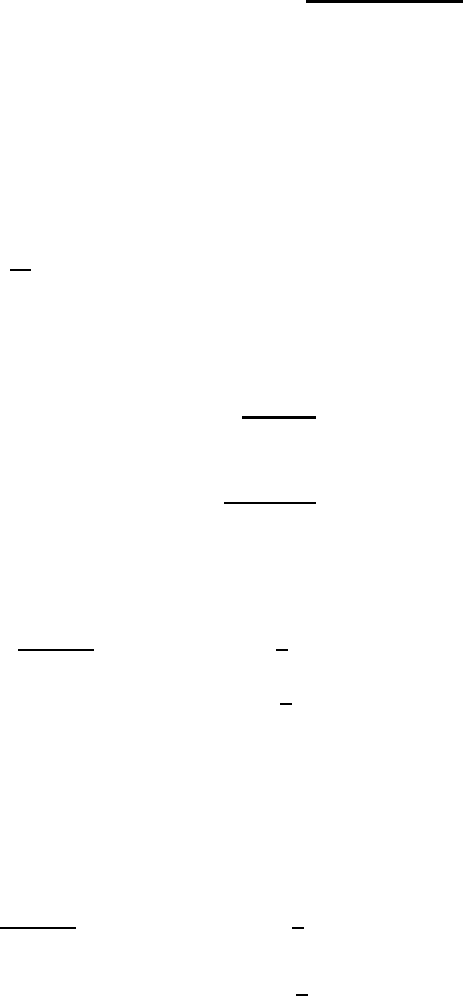
332 An excursion into spectral turbulence theory
where the summation over all amplitude vectors must be carried out. For each
individual component k we may write
E(k,t) =
V(k,t) · V(−k,t)
2
(12.23)
As before, the conjugated velocity amplitude vector is obtained by formally replac-
ing k by −k,thatis
V(k,t) = V(−k,t). Summing over all k gives the total kinetic
energy
E(t) =
∞
k=−∞
E(k,t)(12.24)
thus repeating (12.22). In order to find a prognostic equation for E(k,t), we first
replace the wavenumber vector k in (12.21) by −k to give
∂
∂t
+ νk
2
V(−k,t) =−i(−k,t)(−k) + ik · V(m,t)V(−k − m,t)(12.25)
Next we carry out two scalar multiplications by multiplying (12.21) by V(−k,t)
and (12.25) by V(k,t). By observing the orthogonality relation stated in (12.15),
the terms multiplying the function disappear. The result is shown in
V(−k,t) ·
∂V(k,t)
∂t
+ νk
2
V(−k,t) · V(k,t)
=−ik · V(m,t)V(k − m,t) · V(−k,t)
V(k,t) ·
∂V(−k,t)
∂t
+ νk
2
V(k,t) · V(−k,t)
= ik · V(m,t)V(−k − m,t) · V(k,t)
(12.26)
Adding these two equations and using the definition (12.23) gives the budget
equation for the amplitude of the kinetic energy per unit mass
∂E(k,t)
∂t
+ 2νk
2
E(k,t) =−
i
2
k · V(m,t)V(k − m,t) · V(−k,t)
+
i
2
k · V(n,t)V(−k − n,t) · V(k,t)
(12.27a)
Summation over m and n is implied. From (12.24) it follows that E(t) is a real
number. At first glance the right-hand side, however, appears to be a complex
quantity, but all imaginary terms will cancel out in the summation over m and n
from minus to plus infinity. In order to get a more concise form of (12.27a), we
substitute into the first term on the right-hand side k
= k −m and in the last term
we use −k
=−k − n. Thus, we obtain
∂E(k,t)
∂t
+ 2νk
2
E(k,t) =−
k
i
2
k · V(k − k
,t)V(k
,t) · V(−k,t)
+
k
i
2
k ·V(k
− k,t)V(−k
,t) · V(k,t)
(12.27b)

12.3 Isotropic conditions 333
where now, in contrast to (12.27a), the summation over k
has been written down
explicitly. Introducing the abbreviation
k
W (k, k
,t) =−
k
i
2
k · V(k − k
,t)V(k
,t) · V(−k,t)
+
k
i
2
k · V(k
− k,t)V(−k
,t) · V(k,t)
(12.28)
leads to the final form of the budget equation for the spectral kinetic energy:
∂E(k,t)
∂t
+ 2νk
2
E(k,t) =
k
W (k, k
,t)
(12.29)
Often the expression W (k, k
,t) is called the energy-transfer function. This function
is antisymmetric, that is W (k, k
,t) =−W (k
, k,t), as follows very easily from
inspection of (12.28). The interpretation of (12.29) is not difficult. The first term
represents the tendency of E to either increase or descrease in time. The second
term on the left-hand side describes the energy dissipation giving that part of the
kinetic energy which is transformed into internal energy. It should be recalled that
the dissipation of short waves greatly exceeds the dissipation of long waves. The
term on the right-hand side of (12.29) represents the exchange of energy of cell
k with neighboring and also with more distant cells. It will be recognized that
the antisymmetric property of the energy-transfer function is closely related to the
principle of conservation of energy. Whatever cell k gains from cell k
is a loss
for cell k
infavorofcellk. Moreover, the right-hand side of (12.29) reflects the
nonlinearity of the equation of motion.
12.3 Isotropic conditions, the transition to the continuous wavenumber space
The solution of (12.29) is very complicated because of the dependency of the trans-
fer function on the entire velocity spectrum V(k,t). Therefore, it seems necessary
to introduce simplifying assumptions. A great deal of simplification is obtained by
introducing the so-called isotropic condition so that the directional dependencies
of V and E on the wavenumber vector k are suppressed, that is
V(k,t) −→ V(k, t),E(k,t) −→ E(k, t),
|
k
|
= k (12.30)
The velocity vector and the kinetic energy now depend only on the scalar
wavenumber k andonthetimet. In order to simplify the notation the time
dependencies of all variables will henceforth be omitted, e.g. E(k, t) will simply
be written as E(k).

334 An excursion into spectral turbulence theory
Certainly, the assumption (12.30) results in the desired analytic simplification,
but much of the physical significance is lost since turbulent processes generally
depend on direction. For the isotropic case the spectral energy-budget equation
assumes the form
∂E(k)
∂t
+ 2νk
2
E(k) =
k
W (k, k
)(12.31)
We think of the discrete amplitudes E(k) of the energy spectrum as representing a
certain volume element in k-space. If we divide E(k) by a sufficiently small volume
element V
k
in this space, we obtain a continuous function ρ(k) that is known as
the spectral energy density,
ρ(k) =
E(k)
V
k
(12.32a)
The energy contained within a thin spherical shell of radius k and thickness k is
then given by
ρ(k) V
k
= 4πk
2
ρ(k) k = E(k) = "(k) k (12.32b)
with V
k
= 4πk
2
k. Here we have also introduced the energy "(k) per unit
wavenumber, given by "(k) = 4πk
2
ρ(k). On dividing (12.31) by V
k
we obtain
the budget equation for the energy density:
∂ρ(k)
∂t
+ 2νk
2
ρ(k) =
1
V
k
k
W (k, k
)
(12.33)
Multiplication of (12.33) by 4πk
2
results in a budget equation for the energy per
unit wavenumber:
∂"(k)
∂t
+ 2νk
2
"(k) =
4πk
2
V
k
k
W (k, k
)(12.34)
In order to treat the interaction of wavenumber k with all other wavenumbers k
we
replace the summation over k
by an integral over the volume dV
k
= 4π (k
)
2
dk
.
By introducing the function
T (k, k
) =
4πk
2
V
k
W (k, k
)
4π(k
)
2
V
k
(12.35)
into (12.34), we finally obtain the compact form of the budget equation for the
spectral energy per unit wavenumber:
∂"(k)
∂t
+ 2νk
2
"(k) =
∞
0
T (k, k
) dk
(12.36)
12.3 Isotropic conditions 335
It will be observed that T (k, k
) is also antisymmetric since W (k, k
) has this
property. In this prognostic equation the function T (k,k
) describes the exchange
of energy in k-space between shell k and all other shells since the integration ranges
from k
= 0tok
=∞.
Our goal is to get some information about the properties of T (k, k
). This infor-
mation could be obtained by solving the spectral equation of motion (12.25) for
each amplitude V(k) to compute T (k, k
). In order to avoid such complex numerical
calculations, various closure hypotheses have been introduced in order to obtain
T (k, k
) alone from knowledge of the energy spectrum "(k). For a detailed discus-
sion see, for example, Hinze (1959) and Rotta (1972), where an extensive literature
on isotropic turbulence can be found. In the following brief description we shall
only introduce the approach of Heisenberg, who considers the case of stationary
or at least quasi-stationary turbulence. He assumed that the spectrum "(k) can be
divided into two regions that are separated by the wavenumber k = k
∗
.
In the region of small wavenumbers (large wavelengths, region I) where k<k
∗
,
turbulence is strongly influenced by external parameters. Examples would be the
geometric characteristics of the flow domain and the type of turbulence generation.
For this region it is not possible to draw general conclusions about the energy
spectrum and the direction of the energy transport.
In the region of large wavenumbers (small wavelengths, region II) where k>k
∗
,
external influences are not important or do not exist. In this wavenumber range the
spectrum should be characterized by universal laws. In this universality region,the
energy transfer is always directed from smaller to larger wavenumbers. This means
that an energy cascade is taking place, whereby turbulent energy is directed from
smaller to larger wavenumbers, and from these to still larger wavenumbers, until
the energy is finally dissipated at the largest wavenumbers.
Heisenberg postulated that, in this energy transfer, the action of large-
wavenumber eddies upon small-wavenumber eddies is much like the appearance
of an additional viscosity. For this turbulence viscosity within the fluid, in analogy
to the frictional term 2νk
2
ρ(k), he assumed the relationship
T (k, k
) =−2κ
H
k
2
"(k)g(k
,"(k
)) (12.37)
The function g(k
,"(k
)) is thought to be a universal function. The constant of
proportionality κ
H
is known as Heisenberg’s constant, which is a pure number,
κ
H
= 0.5 ± 0.03.
The form of the universal function g follows from a dimensional analysis that is
carried out next. In the mks system the units of energy density per unit mass and
unit wavenumber are ["(k)] = m
3
s
−2
, the units of the time derivative are therefore
∂"(k)/∂t
= m
3
s
−3
. From (12.36) we find the units of T (k, k
)as
T (k, k
)
=

336 An excursion into spectral turbulence theory
Fig. 12.5 A schematic view of energy transfer in region II.
m
4
s
−3
so that the units of g follow immediately from (12.37),
g(k
,"(k
))
=
m
3
s
−1
.Sinceg depends only on k
and "(k
), we may write
g(k
,"(k
)) = (k
)
α
"(k
)
β
(12.38a)
where the exponents α and β must be determined. By comparison with the dimen-
sion of g we find
(k
)
α
"(k
)
β
= m
3
s
−1
. This leads to the values α =−
3
2
and
β =
1
2
. Utilizing these values, for g we finally get the form
g(k
) = (k
)
−3/2
"(k
)
1/2
=
"(k
)
(k
)
3
(12.38b)
Therefore, according to (12.37), the transfer function T (k, k
)isgivenby
T (k, k
) =−2κ
H
k
2
"(k)
"(k
)
(k
)
3
(12.39)
We will now briefly discuss the transfer function T (k, k
) by considering the
energy cascade shown schematically in Figure 12.5. The outflow from cell k to
cell k
>kis directly given by (12.39). Using the fact that the transfer function is
antisymmetric, i.e. T (k,k
) =−T (k
,k), the flow from cell k
to cell k>k
can be
written down directly. This results in
T (k, k
) =
−2κ
H
k
2
"(k)
"(k
)
(k
)
3
k
>k: outflow
2κ
H
(k
)
2
"(k
)
"(k)
(k)
3
k
<k:inflow
(12.40)
12.4 The Heisenberg spectrum
The task ahead is to calculate the energy spectrum for the region k>k
∗
by assuming
stationary conditions. For such conditions it will be necessary to compensate for
the steady loss of turbulence energy by dissipation by gaining an equal amount

12.4 The Heisenberg spectrum 337
of energy in order to maintain stationarity. Therefore, it will be assumed that
production of energy σ (k) takes place in the region k<k
∗
. Eventually, the energy
produced in the production region is transported to the short waves where it will
be dissipated. Instead of equation (12.36) we now write the energy budget as
∂
∂t
+ 2νk
2
"(k) =
∞
0
T (k, k
) dk
+ σ (k)(12.41)
with σ (k) = 0fork> k
∗
. This is the spectral energy-balance equation with
production, keeping in mind that no production is allowed to take place in the
universality range. In order to obtain the budget equation for an entire spectral
interval, we integrate (12.41) over a wavenumber range to the wavenumber k>k
∗
as indicated by
∂
∂t
k
0
"(k
) dk
+ 2ν
k
0
(k
)
2
"(k
) dk
=
k
0
dk
∞
0
T (k
,k
) dk
+
k
0
σ (k
) dk
(12.42)
For stationary conditions the production and dissipation of energy must be balanced:
k
0
σ (k
) dk
= 2ν
∞
0
(k
)
2
"(k
) dk
= "
M
with
k
0
σ (k
) dk
=
∞
0
σ (k
) dk
(12.43)
since σ (k
) = 0fork
>k
∗
.Here"
M
is the dissipation of energy per unit mass.
Setting the tendency term in (12.42) equal to zero and using (12.43), we may write
2ν
k
0
(k
)
2
"(k
) dk
=
k
0
dk
∞
0
T (k
,k
) dk
+ "
M
=
k
0
dk
∞
k
T (k
,k
) dk
+ "
M
since T (k
,k
) =−T (k
,k
) =⇒
k
0
dk
k
0
T (k
,k
) dk
= 0
(12.44)
On substituting the transfer function T (k, k
) according to (12.39) into this equation,
the spectral energy equation for stationary conditions can be written as
ν + κ
H
∞
k
"(k
)
(k
)
3
dk
2
k
0
(k
)
2
"(k
) dk
= "
M
(12.45a)
The integral expression within the large parentheses,
K = κ
H
∞
k
"(k
)
(k
)
3
dk
(12.45b)

338 An excursion into spectral turbulence theory
is known as the Heisenberg exchange coefficient K, which depends on " and
on the wavenumber k. We observe that, for large k (small wavelengths), the
exchange coefficient is small, tending to zero as k tends to infinity. In this case
the entire energy loss is then due to molecular dissipation. If "(k
) is zero, then
the exchange coefficient is zero as well. In order to give a quantitative treatment
of the exchange coefficient, we must have information on ". Later we will try to
express "(k) as a function of K.
We are now going to calculate the energy spectrum from equation (12.45). For
this we define the integral multiplying the bracket in (12.45) by
y(k) = 2
k
0
(k
)
2
"(k
) dk
(12.46a)
so that (12.45) can be written as
ν + κ
H
∞
k
y
(k
)
2(k
)
5
dk
=
"
M
y(k)
(12.46b)
Here y
= dy/dk = 2k
2
"(k), which follows from the differentiation of (12.46a)
with respect to the variable upper integration limit k. Differentiating (12.46b) with
respect to k and squaring the result gives
κ
2
H
2k
5
=
"
2
M
y
4
(k)
y
(12.46c)
This expression is integrated by separating the variables, yielding
κ
2
H
8k
4
+ C =
"
2
M
3y
3
(k)
(12.46d)
The constant of integration C is found from the definition of
"
M
given by (12.43):
"
M
= 2ν
∞
0
(k
)
2
"(k
) dk
= ν lim
k→∞
y(k) =⇒ y(∞) =
"
M
ν
(12.46e)
where (12.46a) has been used. Therefore, for k →∞we obtain from (12.46d)
C =
"
M
/[3y(∞)] = ν
3
/(3"
M
). Substituting this expression into (12.46d) and
solving for y gives
y(k) =
"
2/3
M
3
1/3
κ
2
H
8k
4
+
ν
3
3"
M
−1/3
(12.46f)
Differentiating this equation with respect to k with dy/dk = y
= 2k
2
"(k)and
then solving for "(k)gives
"(k) =
"
2/3
M
3
1/3
2
3
κ
2
H
8k
4
+
ν
3
3"
M
−4/3
κ
2
H
8k
7
,k>k
(12.46g)
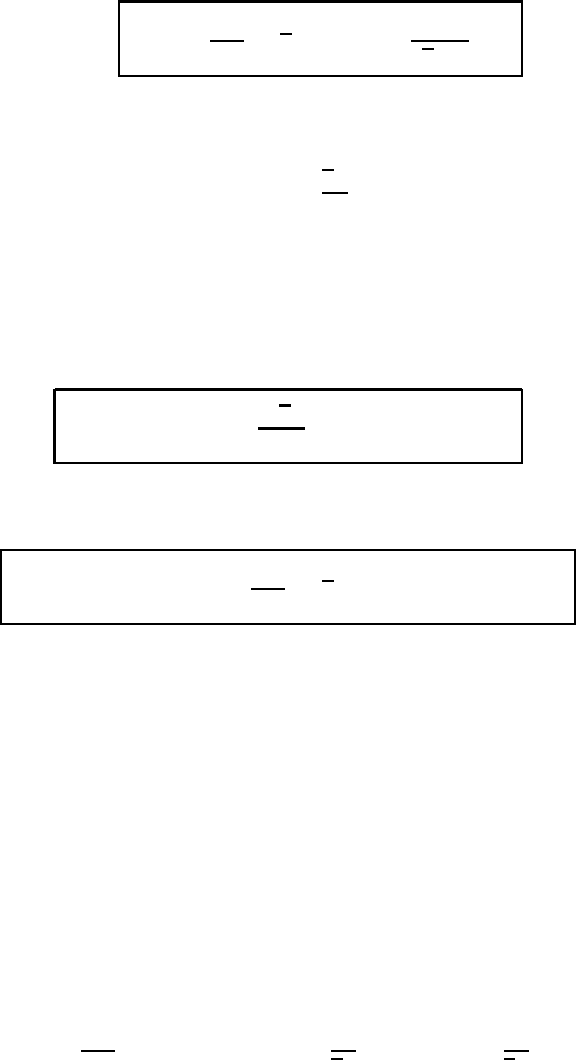
12.4 The Heisenberg spectrum 339
This can be rewritten in the form
"(k) =
8
9κ
H
2/3
"
2/3
M
k
−5/3
1 +
8ν
3
k
4
3"
M
κ
2
H
−4/3
(12.47)
First of all we observe from (12.47) that the spectrum may be separated into two
wavenumber regions by the wavenumber k
c
,givenby
k
c
=
"
M
ν
3
1/4
(12.48)
since for k>k
c
the second expression within the second set of parentheses exceeds
the number 1 by at least one order of magnitude. Ignoring the number 1 within the
parantheses, we obtain the section of the spectrum to the far right. This wing is
known as the dissipation range, where the energy spectrum decays with the minus
seventh power of k:
k>k
c
: "(k) =
κ
H
"
M
2ν
2
2
k
−7
=⇒ "(k) ∼ k
−7
(12.49)
Now we consider the region defined by k
∗
<k k
c
. By omitting now from
(12.47) the second expression within the parentheses we obtain
k
∗
<k k
c
: "(k) =
8
9κ
2
H
2/3
"
2/3
M
k
−5/3
=⇒ "(k) ∼ k
−5/3
(12.50)
Hence, it is seen that, in the long-wave spectral range, "(k) is proportional to k
−5/3
.
This phenomenon is called the k
−5/3
law. The spectral range for which the k
−5/3
law is valid is known as the transfer region or the inertial subrange since in this
region the viscosity may be neglected. The physical picture is that production
and dissipation occur in different spectral regions so that the eddies in the inertial
subrange receive their energy initially from the larger eddies and transfer their
energy to the smaller eddies. The transfer takes place at such a rate that production
is exactly balanced by dissipation. Observations show that, in the production range
(k<k
∗
), the left wing of the energy spectrum falls off to the fourth power. For the
whole spectrum the distribution of "(k) is schematically shown in Figure 12.6.
Often equation (12.47) is written in a somewhat different way by introducing the
Kolmogorov constant κ
K
, the characteristic length l
c
, and the characteristic time t
c
defined by
κ
K
=
8
9κ
H
2/3
= 1.44,l
c
=
ν
3
"
M
1/4
,t
c
=
ν
"
M
1/2
(12.51)
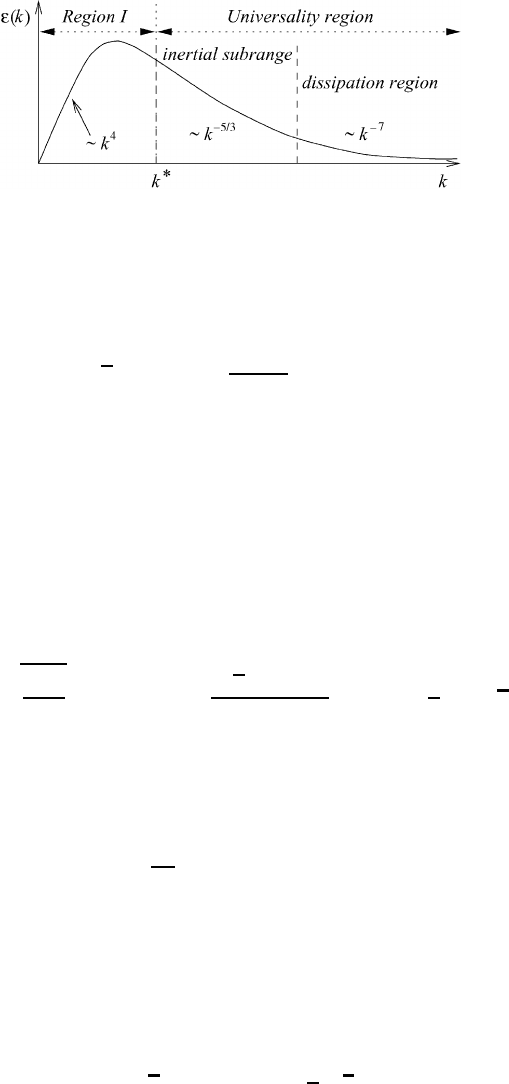
340 An excursion into spectral turbulence theory
Fig. 12.6 The Heisenberg spectrum.
with κ
H
= 0.51. The Kolmogorov constant is named after the scientist who
pioneered research into turbulence spectra. Substituting κ
K
and l
c
into (12.47),
the energy spectrum may be written as
"(k) = κ
K
"
2/3
M
k
−5/3
1 +
8(kl
c
)
4
3κ
2
H
−4/3
,k>k
∗
(12.52)
This new notation, of course, does not change the physical content of the energy
spectrum. Now the long-wave range is isolated by means of kl
c
1 and the short
-wave range by kl
c
1.
12.5 Relations for the Heisenberg exchange coefficient
The task ahead is to evaluate the integral (12.45b) defining the Heisenberg exchange
coefficient. This will be accomplished by first substituting the energy expression for
the long-wave approximation (12.50) for the stationary case into (12.45b), yielding
K = κ
H
∞
k
"(k
)
(k
)
3
dk
= κ
H
∞
k
κ
K
"
2/3
M
(k
)
−5/3
(k
)
3
1/2
dk
=
3
4
κ
1/2
K
κ
H
"
1/3
M
k
−4/3
(12.53)
We now assume that the wavenumber k separates the short-wave region from the
long-wave region. Then we can express the average kinetic energy
v
2
/2ofthe
longer waves by
v
2
2
=
k
0
"(k
) dk
(12.54a)
and the turbulent kinetic energy
k of the shorter waves by
k =
∞
k
"(k
) dk
(12.54b)
We substitute the spectral energy approximation for the inertial subrange (12.50)
into (12.54b) and obtain
k = κ
K
∞
k
"
2/3
M
(k
)
−5/3
dk
=
3
2
κ
K
"
2/3
M
k
−2/3
(12.55)
