Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

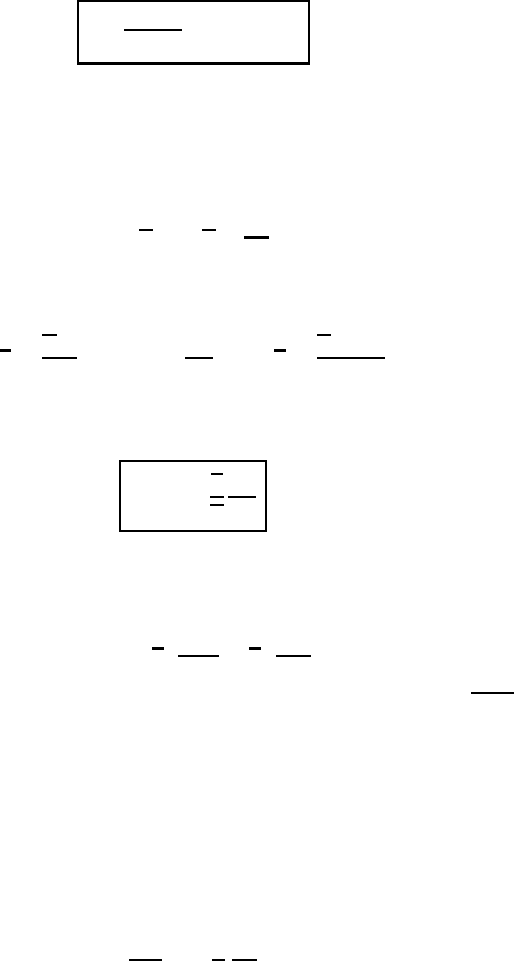
13.3 The Monin–Obukhov similarity theory of the neutral Prandtl layer 361
13.3.3 The characteristic length or the mixing length
The ratio formed by the frictional velocity and the vertical gradient of the horizontal
velocity has the dimension of a length. We use this ratio to define the mixing length
l for neutral conditions:
l =
u
∗
∂u/∂z
=⇒ l = kz
(13.51)
The last expression follows immediately from (13.45). Later we will assume that
the first expression is also valid in the diabatic Prandtl layer. The physical meaning
of the mixing length will be briefly illuminated in Appendix B of this chapter. From
(13.28) and (13.51) we find
τ =
ρu
2
∗
= ρl
2
∂u
∂z
2
(13.52)
Using the definition of the mixing length, equations (13.48) and (13.50) can be
rewritten as
=
ρu
3
∗
l
,u
∗
=
K
v
l
=⇒
=
ρ (K
v
)
3
l
4
(13.53)
showing the relation among the dissipation of energy, the exchange coefficient, and
the mixing length. Finally, we can rewrite (13.53) to obtain
(K
v
)
2
=
ρ
l
4
K
v
(13.54)
In (12.59b) we have derived the Heisenberg relation for the exchange coefficient
from spectral analysis using the conditions of isotropic turbulence. This relation
may be written as
(K
v
)
2
=
M
b
3
l
4
aK
v
=
M
(l
)
4
K
v
(13.55)
For ease of comparison we have introduced the mixing length (l
)
2
= l
2
b
3
/a into
this equation. Apart from a constant that includes the density, these two formulations
obtained in entirely different ways are identical. Therefore, equation (13.54) is also
known as Heisenberg’s relation. This leads us to assume that (13.54) is valid also
for non-neutral conditions.
Finally, we will derive another formula for the mixing length, which is attributed
to Von Karman. We proceed as follows. We differentiate (13.45) with respect to z
and recall that the frictional velocity is a constant. This yields
∂
2
u
∂z
2
=−
k
l
∂u
∂z
(13.56)
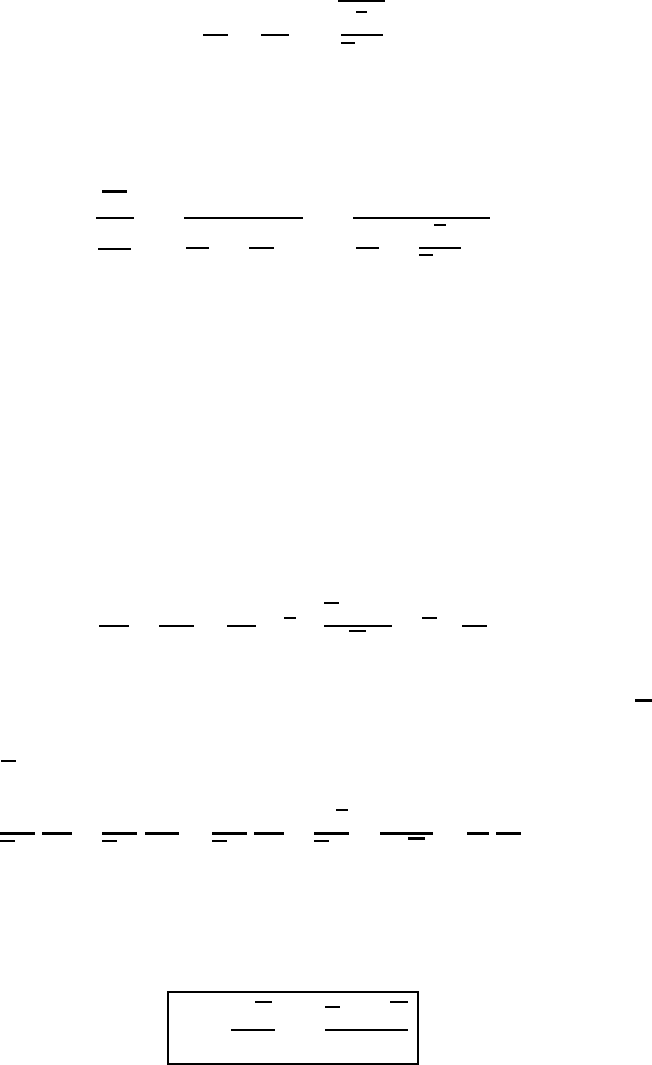
362 The atmospheric boundary layer
From (13.45), (13.50), and (13.54) we obtain
∂u
∂z
=
K
v
l
2
=
ρK
v
(13.57)
The latter two equations lead directly to the VonKarmanrelationof the mixing
length:
l =−k
∂u
∂z
∂
2
u
∂z
2
=−
k
∂
∂z
ln
∂u
∂z
=−
2k
∂
∂z
ln
ρK
v
(13.58)
We should realize that the two definitions of the mixing length (13.51) and (13.58)
are not independent of each other. If we try to extrapolate the mixing-length
formulas of the neutral Prandtl layer to the non-neutral or diabatic Prandtl layer we
must select one of these formulations.
13.4 The Monin–Obukhov similarity theory of the diabatic Prandtl layer
We will now consider the diabatic or non-neutral Prandtl layer. The starting point
of the analysis is the general Prandtl-layer energy budget. Addition of the last two
equations of (13.25) and utilizing (13.51) and (13.52) results in
∂E
∂z
+
∂W
∂z
=
∂E
∂z
+
+
ρgu
∗
T
∗
T
=
ρu
2
∗
∂u
∂z
(13.59)
where we have expressed the heat flux according to (13.28). We consider not
only the density to be independent of height but also the average temperature
T
whenever it appears in undifferentiated form. We multiply all terms of this equation
by kz/
ρu
3
∗
and find the relations
kz
ρu
3
∗
∂E
∂z
+
kz
ρu
3
∗
∂W
∂z
=
kz
ρu
3
∗
∂E
∂z
+
kz
ρu
3
∗
+
kzgT
∗
u
2
∗
T
=
kz
u
∗
∂u
∂z
(13.60)
Each term of this equation now is dimensionless, which is most easily verified by
inspecting the last term on the right-hand side. The last term on the left-hand side
can be written as z/L
∗
,whereL
∗
has the dimension of a length with
L
∗
=
u
2
∗
T
gkT
∗
=−
ρc
p,0
u
3
∗
T
gkH
(13.61)
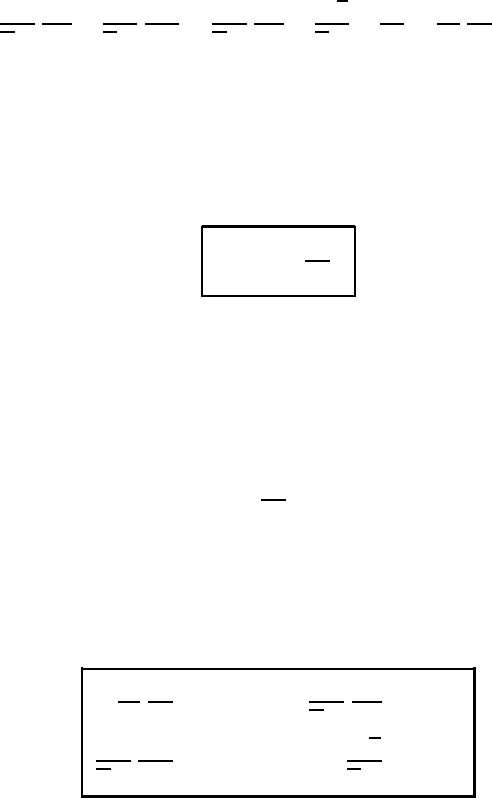
13.4 The Monin–Obukhov similarity theory of the diabatic Prandtl layer 363
This length is known as the Monin–Obukhov length and is of special significance
in the work to follow. Within the Prandtl layer L
∗
is a height-independent quantity.
Inserting L
∗
into (13.60) gives
kz
ρu
3
∗
∂E
∂z
+
kz
ρu
3
∗
∂W
∂z
=
kz
ρu
3
∗
∂E
∂z
+
kz
ρu
3
∗
+
z
L
∗
=
kz
u
∗
∂u
∂z
(13.62)
We introduce the dimensionless vertical coordinate
ξ = z/L
∗
(13.63)
Any function S depending solely on ξ and possibly on universal numbers is called
a Monin–Obukhov function:
S(ξ) = S
z
L
∗
(13.64)
The basic idea of the similarity theory of the diabatic Prandtl layer is that the
relationship (13.41) pertaining to the neutral atmosphere may be extended to the
non-neutral atmosphere by including the variable L
∗
in the wind-profile analysis. In
other words, it is assumed that there exists a unique relationship among the variables
z, u
∗
,∂u/∂z,andL
∗
. The functional relation describing this is expressed by
F
z, u
∗
,
∂u
∂z
,L
∗
= 0(13.65)
Using dimensionless analysis, we show in Appendix A, Example 2, that the last
expression of (13.62) is a MO function. Furthermore, the MO theory also assumes
that not only the last term of (13.62) but also every other term occurring in this
equation is a MO function so that we may write
kz
u
∗
∂u
∂z
= S
u
(ξ),
kz
ρu
3
∗
∂E
∂z
= S
E
(ξ)
kz
ρu
3
∗
∂W
∂z
= S
W
(ξ),
kz
ρu
3
∗
= S
(ξ)
(13.66)
By integrating the first of these equations we obtain the vertical wind profile of the
diabatic Prandtl layer. This topic will be discussed later. Using these definitions
equation (13.62) can now be rewritten in the form of two independent equations:
S
E
(ξ) + S
W
(ξ) = S
E
(ξ) + S
(ξ) + ξ = S
u
(ξ)(13.67)
In order to obtain information on the temperature profile and on the specific hu-
midity profile we additionally assume relations anlogous to (13.66):
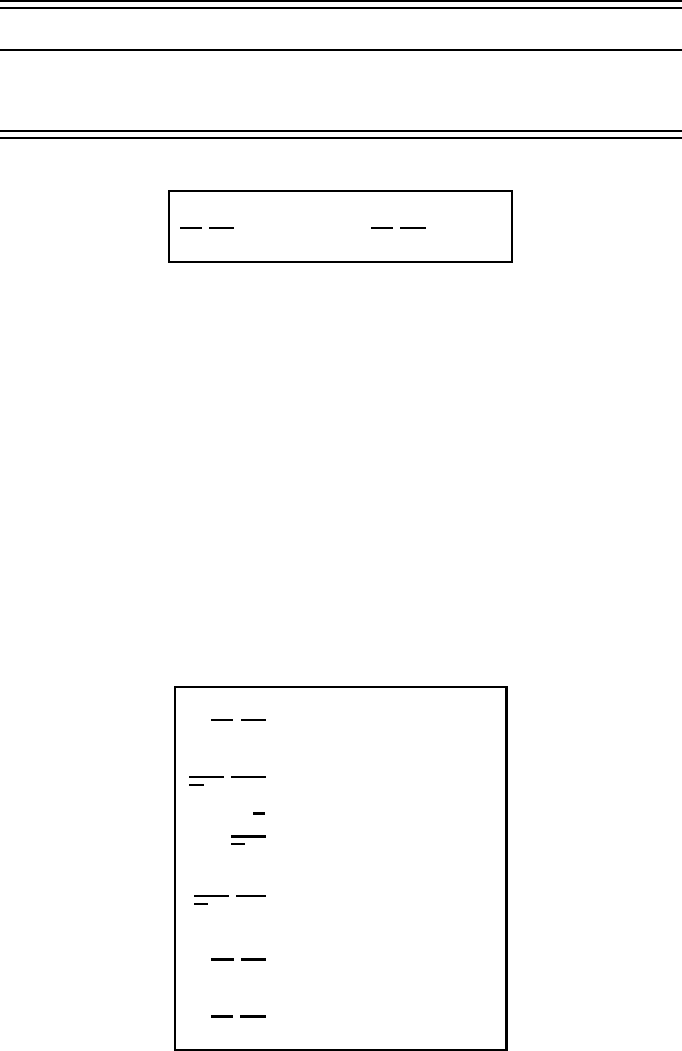
364 The atmospheric boundary layer
Table 13.1. Sign conventions for various quantities as functions of the
atmospheric stratification
Stratification ∂
θ/∂z H T
∗
,ξ,Ri
f
L
∗
Stable >0 <0 >0 >0
Neutral 0 0 0 ±∞
Unstable <0 >0 <0 <0
kz
T
∗
∂
θ
∂z
= S
T
(ξ),
kz
q
∗
∂q
∂z
= S
q
(ξ)
(13.68)
We close this section by summarizing in Table 13.1 the sign conventions for
various important quantities. It will be seen, for example, that, for stable and
unstable stratifications, the heat flux H and the MO length L
∗
have opposite signs.
For neutral conditions the heat flux is zero and L
∗
is ±∞. An important reference
is Obukhov (1971), who reviews the basic concepts of the similarity theory.
13.4.1 The determination of the Monin–Obukhov functions
We recall that there exist only two independent equations (13.67) to determine the
four MO functions S
E
(ξ),S
(ξ),S
u
(ξ), and S
W
(ξ). Therefore, it will be necessary to
make additional assumptions. Since L
∗
approaches ±∞ for neutral conditions, the
dimensionless height ξ approaches zero and the MO functions (with the exception
of S
E
(ξ)) must be equal to unity so that they reduce to the corresponding relations
of the neutral Prandtl layer. In summary, we have for ξ = 0
kz
u
∗
∂u
∂z
= 1 =⇒ S
u
(ξ = 0) = 1
kz
ρu
3
∗
∂W
∂z
= 1 =⇒ S
W
(ξ = 0) = 1
kz
ρu
3
∗
= 1 =⇒ S
(ξ = 0) = 1
kz
ρu
3
∗
∂E
∂z
= 0 =⇒ S
E
(ξ = 0) = 0
kz
T
∗
∂
θ
∂z
= 1 =⇒ S
T
(ξ = 0) = 1
kz
q
∗
∂q
∂z
= 1 =⇒ S
q
(ξ = 0) = 1
(13.69)
13.4 The Monin–Obukhov similarity theory of the diabatic Prandtl layer 365
Next we will introduce the definition of the MO length L
∗
into the flux Richardson
number (13.34). This results in
Ri
f
=
ξ
kz
u
∗
∂u
∂z
=
ξ
S
u
(ξ)
(13.70)
showing that the MO function S
u
(ξ) for the velocity may be expressed in terms of
the dimensionless number Ri
f
.
On the basis of observational data various empirical relations have been proposed
for the various MO functions. For S
u
(ξ)weuse
S
u
(ξ) = (1 − 2αRi
f
)
−1/4
≈ 1 +
α
2
Ri
f
≈ 1 +
α
2
ξ with α = 7(13.71)
which is due to Ellison (1957). Utilizing only the first two terms of the expansion
of the fourth root we obtain an expression attributed to Monin and Obukhov
(1954). This approximation will now be used to generalize the logarithmic wind
law (13.46). From (13.66) we find immediately
kz
u
∗
∂u
∂z
= S
u
(ξ) = 1 +
α
2
ξ (13.72)
Integration with respect to height gives
u =
u
∗
k
ln
z
z
0
+
α(z − z
0
)
2L
∗
(13.73)
which is known as the log–linear wind profile. Since the expansion of the MO
function S
u
(ξ) was discontinued after the linear term, we may expect reasonable
accuracy in the reproduction of the wind field only for conditions not too far
removed from neutral stratification. Figure 13.3 shows qualitatively the vertical
wind profile in the Prandtl layer for stable, neutral, and unstable stratification. For
unstable stratification with L
∗
< 0 the wind speed for a given height is less than
that for neutral conditions. For stable stratification with L
∗
> 0 the wind speed for
a given height is larger than that for neutral conditions.
13.4.2 The KEYPS and the extended KEYPS formula
There exists a semi-empirical equation for the determination of S
u
, which is known
as the KEYPS formula. This curious name is the contraction of the names of the

366 The atmospheric boundary layer
Fig. 13.3 Logarithmic and log–linear wind profiles for different stratifications.
five scientists Kondo, Ellison, Yamamoto, Panowski, and Sellers who derived this
formula independently. Since this equation is used frequently for Prandtl-layer
investigations it will be derived next. All that needs to be done is to take the fourth
power of (13.71), yielding
S
4
u
− 2αξS
3
u
= 1
(13.74)
Solutions to this equation give information on the MO function S
u
. Some remarks
on this formula may be helpful. There should be agreement between the KEYPS
formula and the more general equation (13.67). On multiplying this equation by
S
3
u
we obtain
S
4
u
− ξS
3
u
1 +
S
E
ξ
= S
S
3
u
(13.75)
Agreement with the KEYPS formula requires the validity of
S
S
3
u
= 1, 1 +
S
E
ξ
= 2α (13.76)
as follows from comparison with (13.74). Replacing both MO functions in the first
equation of (13.76) with the help of (13.66) yields
kz
ρu
3
∗
=
u
∗
kz
∂u
∂z
3
=
K
v
kzu
∗
3
(13.77)
where (13.49) has also been used to eliminate ∂u/∂z. We now compare (13.77)
with (13.54), which is considered a valid statement since it can also be derived
from spectral theory without using Prandtl-layer assumptions. We find agreement
only if the mixing length in the diabatic Prandtl layer is also given by l = kz.This
result, however, is in conflict with equation (13.51) due to (13.66). Therefore, some
criticism of the KEYPS equation or of Ellison’s formula (13.71) is justified.

13.4 The Monin–Obukhov similarity theory of the diabatic Prandtl layer 367
Finally, let us consider (13.67) showing the expected relation between S
E
(ξ)and
the other MO functions. Measurements indicate that, at least in the unstable Prandtl
layer, the MO function S
E
does not linearly depend on ξ as required by (13.76).
In the following we will attempt to eliminate the defect in the KEYPS equation.
The starting point of the analysis is (13.53). A relationship of this form was also
derived from spectral analysis (see also (13.55)) for the special case of isotropic
turbulence but independent of Prandtl-layer assumptions. Therefore, we have rea-
son to believe that (13.53) can be generalized. On combining this equation with
(13.49), which is valid for the diabatic as well as for the neutral Prandtl layer, we
obtain
ρ
=
u
6
∗
l
4
∂u
∂z
3
=⇒
kz
ρu
3
∗
l
kz
4
=
kz
u
∗
∂u
∂z
−3
(13.78)
In this equation the characteristic or mixing length l is still undetermined. In fact,
all we know about the mixing length is that l = kz in the neutral Prandtl layer. By
introducing into (13.78) the MO relations (13.66) we obtain
S
l
kz
4
=
1
S
3
u
or
l
kz
4
=
1
S
S
3
u
(13.79)
Since S
(ξ)andS
u
(ξ) depend only on the dimensionless height, we consider the
expression l/(kz) as the definition of another MO function, that is
S
l
(ξ) =
l
kz
,S
l
(ξ = 0) = 1(13.80)
We also require that S
l
(ξ = 0) = 1 since in the neutral case l/(kz) = 1. Thus,
we have introduced an additional MO function that is related to S
and S
u
.From
(13.79) we find
S
S
3
u
S
4
l
= 1(13.81)
which should also be valid in the diabatic Prandtl layer. This relation makes it
possible to eliminate S
(ξ) from the budget equation (13.67). Substitution of S
(ξ)
then gives
S
E
+ S
+ ξ = S
E
+
1
S
4
l
S
3
u
+ ξ = S
u
(13.82)
Rewriting the latter expression results in the extended KEYPS equation:
S
4
u
− ξS
3
u
1 +
S
E
ξ
=
1
S
4
l
(13.83)
368 The atmospheric boundary layer
This equation is considered to be rigorously correct within the framework of
the Prandtl-layer theory. Unless we are able to determine S
l
as a function of
the dimensionless height we have not gained anything. There exists an empirical
relation for S
l
due to Takeuchi and Yokoyama (1963), which reduces to S
l
(ξ =
0) = 1 as it should. However, in some parts of the unstable Prandtl layer problems
arise with that empirical formula. In the following we are not going to discuss this
formula, but we will try to find an analytic relation between S
l
and S
u
(ξ).
13.4.3 An analytic relation between the MO Functions S
l
and S
u
In order to find an analytic relation between S
l
and S
u
we must first derive a relation
for the mixing length that is valid also in the diabatic atmosphere. We may select
either the Prandtl relation (13.51) or the Von Karman relation (13.58). These two
equations are not independent in the neutral Prandtl layer. First we use the Prandtl
relation. Dividing (13.51) by kz and utilizing (13.66) and (13.80) gives
l
kz
=
1
kz
u
∗
∂u
∂z
=
1
S
u
=⇒ l =
kz
S
u
,S
l
=
1
S
u
(13.84)
It is more difficult but also straightforward to apply the Von Karman relation
(13.58). On rewriting the logarithm in (13.58) by means of (13.49), (13.66), and
(13.81) as
ρK
v
=
S
S
u
u
2
∗
(kz)
2
=
u
2
∗
kzS
2
l
S
u
2
(13.85)
we obtain from the Von Karman relation (13.58)
l =−
2k
∂
∂z
ln
ρK
v
=
k
∂
∂z
ln
zS
2
l
S
u
=⇒
S
l
=
l
kz
=
1
z
∂
∂z
ln
zS
2
l
S
u
=
1
ξ
d
dξ
ln
ξS
2
l
S
u
=
1
1 +
2ξ
S
l
dS
l
dξ
+
ξ
S
u
dS
u
dξ
(13.86)
since ξ = z/L
∗
and L
∗
= constant. The last equation may be rewritten as
2ξ
dS
l
dξ
+ S
l
1 +
ξ
S
u
dS
u
dξ
= 1(13.87)
This ordinary linear differential equation can be solved without difficulty by stan-
dard methods. The solution is
S
l
(ξ) =
1
2
√
ξS
u
(ξ)
ξ
0
S
u
(ξ
)
ξ
dξ
(13.88)
13.5 Application of the Prandtl-layer theory in models 369
We will now summarize how we find the various MO functions. Suppose that
the function S
u
is known. An empirical formula for S
u
will be given soon. Then S
l
can be found either from (13.84) or from (13.88). S
then follows from (13.81) and
S
E
and S
W
from (13.67). The MO functions S
T
and S
q
(13.68) cannot be found in
this manner, but must be obtained in some other way.
From numerous measurements various empirical formulas have been derived for
the MO functions. Frequently the so-called Dyer–Businger equations are used to
state S
u
for stable, neutral, and unstable stratification. These are
S
u
= 1 + 5ξξ≥ 0, stable stratification
S
u
= (1 − 15ξ)
−1/4
ξ ≤ 0, unstable stratification
(13.89)
The MO function S
T
for the transport of sensible heat is usually given in the form
S
T
= (1 + 5ξ ) ξ ≥ 0, stable stratification
S
T
= (1 − 15ξ)
−1/2
ξ ≤ 0, unstable stratification
(13.90)
Moreover, often it is assumed that S
q
= S
T
.
A search of the literature shows that not all authors use identical empirical
equations for the MO functions but mostly something similar to them. Let us
now turn to the defining equation (13.35) of the Prandtl number. Measurements
show that, for neutral conditions, this number should be close to 1.35. Sometimes
the right-hand sides of (13.90) are multiplied by the factor 1/1.35 = 0.74. This,
however, would violate the requirement S
T
(ξ = 0) = 1.
13.5 Application of the Prandtl-layer theory in numerical prognostic models
A brief outline of how the Prandtl-layer theory can be applied to numerical weather
prediction and mesoscale analysis will be given. The lowest surface of the numerical
grid within the atmosphere is selected to coincide with the roughness height z
0
,
which is assumed to be known. A neighboring surface is fixed somewhere within
the Prandtl layer, for example, at the height h. We assume that the numerical model
is capable of calculating mean values of the horizontal velocity, the temperature (or
potential temperature), the density, the pressure, and the specific humidity at these
two surfaces. These mean variables are called the external parameters whereas L
∗
is known as an internal parameter. By the methods of the previous section we are
in a position to calculate all required MO functions. Let us assume that all of these
are at our disposal when needed. On integrating the relations (13.66) and (13.68)
between the roughness height z
0
and h we find

370 The atmospheric boundary layer
u(h) =
u
∗
k
h
z
0
S
u
(ξ)
dz
z
, u(z
0
) = 0
θ(h) −
θ(z
0
) =
T
∗
k
h
z
0
S
T
(ξ)
dz
z
with ξ =
z
L
∗
(13.91)
The left-hand sides are the external parameters which are considered known. The
scaling parameters, the undifferentiated temperature, and the density are treated
as constants in the height integrations within the Prandtl layer. With (13.61) and
(13.91) we have three equations for the determination of u
∗
,T
∗
,andL
∗
.The
solution of this system is best carried out by an iterative procedure. Momentarily
let us assume that the MO functions S
u
and S
T
can be expressed as linear functions
of ξ , which is the case for the stable Prandtl layer as expressed by (13.89) and
(13.90). For the unstable case the expansion of the MO functions would have to
be discontinued after the linear term. Therefore, we may write for the two MO
functions the following two expressions:
S
u
≈ 1 + α
u
ξ, S
T
≈ 1 + α
T
ξ (13.92)
The quantities α
u
and α
T
are the expansion coefficients.
By substituting (13.92) into (13.91) we may carry out the integration. The result
is
u(h) =
u
(n)
∗
k
ln
h
z
0
+
α
u
(h − z
0
)
L
(n−1)
∗
θ(h) −
θ(z
0
) =
T
(n)
∗
k
ln
h
z
0
+
α
T
(h − z
0
)
L
(n−1)
∗
L
(n−1)
∗
=
T
gk
u
2
∗
T
∗
n−1
,L
(0)
∗
=∞
(13.93)
The first equation of (13.93) was already stated earlier in (13.73) and describes the
log–linear wind profile. Since the system (13.93) must be solved iteratively for u
∗
and T
∗
, we have added the iteration index as the superscript n. With the exception
of u
∗
and T
∗
all remaining quantities are known. The heights z
0
and h are specified.
The scaling height L
∗
is evaluated at the previous time step. To get the iteration
started, we assume that we have neutral conditions so that L
(0)
∗
=∞. Equations
(13.93) can be easily solved for u
(n)
∗
and T
(n)
∗
. Let us now assume that u
∗
,T
∗
,and
L
∗
have been found by iterating sufficiently many times that u
∗
and T
∗
no longer
change within a prescribed tolerance. This is sufficient to calculate the stress τ and
the heat flux H from equation (13.28).
If the linear expansions of the MO functions S
u
and S
T
are considered insufficient,
for unstable stratification the full expressions must be used. Equation (13.91) can
