Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

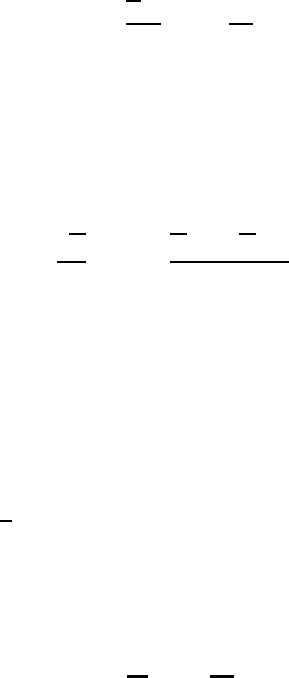
13.6 Fluxes, dissipation of energy, and exchange coefficients 371
still be solved by the same iterative procedure, but the integrals must be solved
numerically. The remaining undetermined quantities will be discussed in the next
section.
13.6 The fluxes, the dissipation of energy, and the exchange coefficients
The MO function S
W
can be computed as described in Section 13.4.3 and is
considered known. The height integration of (13.66) results in
W (h) − W (z
0
) =
ρu
3
∗
k
h
z
0
S
W
dz
z
(13.94)
The definition of this heat flux is given by (13.24). Owing to the pressure fluctuation
, W is expected to be very small and often may be neglected altogether. W (z
0
)
is unknown and cannot be determined from Prandtl-layer theory. We assume that
the turbulent part of W (z
0
) vanishes and approximate W (z
0
)bythemolecular
conduction of heat as
W (z
0
) =−l
c
∂
T
∂z
z
0
≈−l
c
T (h) − T (z
0
)
h − z
0
(13.95)
where l
c
is the heat-conduction coefficient.
The quantity E appearing in the budget equation (13.25) for the turbulent kinetic
energy cannot be calculated from the differential equation (13.66) since an integra-
tion constant for some point in the Prandtl layer is not available. The calculation of
E, however, is not at all necessary since it does not appear in the prognostic system.
It does, however, appear in the prognostic equation for the turbulent kinetic energy
k, which is a subgrid quantity; see (11.46) and (13.13).
The dissipation of energy
given in (13.66) can be determined for all heights in
the Prandtl layer since the MO function S
is considered known.
The flux of water vapor Q can be found from (13.28). q
∗
is obtained by solving
the corresponding differential equation (13.68). Integration gives
q(h) −q(z
0
) =
q
∗
k
h
z
0
S
q
dz
z
(13.96)
Since q(h)andq(z
0
) are known external parameters and the MO function S
q
= S
T
is known also, the height-constant scaling parameter q
∗
can be calculated and then
be substituted into (13.28) to find the moisture flux.
Most mesoscale models resolve the Prandtl layer by including additional grid
surfaces. The phenomenological coefficients, i.e. the exchange coefficients, may
372 The atmospheric boundary layer
Fig. 13.4 Height profiles of the exchange coefficient.
be determined easily for these grid surfaces. There exist two formulas from which
each exchange coefficient can be found. K
v
is obtained from (13.49) and (13.66);
K
θ
and K
q
follow from combining the relations listed in (13.26), (13.28), and
(13.68). In summary we have
K
v
=
u
2
∗
∂u
∂z
=
kzu
∗
S
u
(ξ)
,K
θ
=
u
∗
T
∗
∂
θ
∂z
=
kzu
∗
S
T
(ξ)
,K
q
=
u
∗
q
∗
∂q
∂z
=
kzu
∗
S
q
(ξ)
(13.97)
The vertical distribution of the exchange coefficient K
v
is shown qualitatively
in Figure 13.4. For a given height K
v
is smaller for stable than it is for neutral and
unstable stratification.
13.7 The interface condition at the earth’s surface
The starting point in the derivation is the prognostic equation (11.49) for the
enthalpy. Owing to the Prandtl-layer condition (13.5) the budget operator vanishes.
We make the addtional assumption that only isobaric processes are admitted and
that transitions between the turbulent kinetic energy and the internal energy do not
take place. In view of Figure 13.2 and equation (12.63) we may summarize the
situation by writing
D
Dt
ρ
h
= 0,
d p
dt
= 0, v
·∇p + = J
θ
t
·∇ln
+ = 0(13.98)
where H = J
θ
t
. With these assumptions equation (11.49) reduces to the following
divergence expression:
∇·
J
h
s,t
+ J
h
s
+
J
n
t
+ J
n
h
n
+ F
R
= 0(13.99)
where the sensible enthalpy fluxes defined in (11.61) have been used. According to
equation (9.6) we must replace the regular divergence by the surface divergence,

13.7 The interface condition at the earth’s surface 373
which is repeated for convenience:
∇·Ψ −→ i
3
· (Ψ
a
− Ψ
g
)(13.100)
The subscripts a and g stand for atmosphere and ground. By ignoring within
the atmosphere the mean molecular sensible enthalpy flux
J
h
s
and replacing the
turbulent sensible enthalpy flux J
h
s,t
by means of (11.69) we find
i
3
·
J
h
s,t
+ J
h
s
a
= i
3
·
J
θ
t
+ J
t
= J
θ
t
(13.101)
The turbulent Exner flux J
t
vanishes since only isobaric processes are admitted.
Assuming that fog does not form, we use the Prandtl-layer formulation (13.20)
together with (13.24) to obtain for the enthalpy term
i
3
·
J
n
t
+ J
n
h
n
a
= l
21
Q (13.102)
Turbulent and latent heat fluxes within the ground are ignored so that
i
3
·
J
h
s,t
+ J
h
s
+
J
n
t
+ J
n
h
n
g
= i
3
· J
h
s,g
=−ρ
g
c
g
K
g
i
3
·∇T
g
=−ρ
g
c
g
K
g
∂T
g
∂z
(13.103)
The terms ρ
g
and c
g
are the density and specific heat of the ground while K
g
is the
thermal diffusivity coefficient. The radiative net flux is given by
i
3
· F
R
= σT
4
S
− F
s
− F
l
(13.104)
where T
S
in the Stefan–Boltzmann law refers to the surface temperature of the
earth. F
s
is the short-wave global net flux (accounting for the albedo of the ground)
and F
l
is the long-wave downward flux. The heat balance at the earth’s surface is
then given by
σT
4
S
− F
s
− F
l
+ J
θ
t
− l
21
Q + ρ
g
c
g
K
g
∂T
g
∂z
= 0(13.105)
In this equation all energy fluxes directed from the surface into the atmosphere or
into the ground are counted as positive.
A more complete formulation of the heat balance at the earth’s surface and the
moisture balance within the soil is given by Panhans (1976), for example. All
modern investigations include the treatment of a vegetation–soil model; see for
example Deardorff (1978), Pielke (1984), Sellers et al. (1986), and Siebert et al.
374 The atmospheric boundary layer
(1992). Owing to the complexity of such models, we refrain from discussing this
subject.
We will give a simple example of a heat-transport problem to which the surface-
balance equation (13.105) can be applied. We assume nocturnal conditions and
ignore latent-heat effects. Often the wind profile in the surface layer may be ex-
pressed by the power law
u =u
1
z
z
1
m
with m =
0.3 strong stable stratification
0.14 neutral stratification
0.05 strong unstable stratification
(13.106)
where the stability exponents have been obtained from observations. z
1
is the
anemometer height at which the wind velocity is measured. We wish to find the
corresponding vertical profile of the exchange coefficient. Assuming constant val-
ues of τ and
ρ, we obtain from (13.26) and (13.106)
τ
ρ
= K
v
∂u
∂z
,
1
u
∂u
∂z
=
m
z
=⇒ K
v
= az
1−m
,a=
τz
m
1
ρ u
1
m
= constant
(13.107)
The heat equation (11.60) will be strongly simplified by assuming that we have a
dry-air atmosphere and by ignoring the molecular heat flux
J
h
s
.Furthermore,letus
disregard the transformation between the turbulent kinetic and the internal energy
so that the heat equation reduces to the simple form
ρc
p,0
T
θ
d
θ
dt
+∇·J
h
s,t
= 0(13.108)
In this simple case we assume that J
h
s,t
may be parameterized analogously to
equation (13.26). Ignoring the advection of the potential temperature
θ,wefind
with T ≈
θ
∂
θ
∂t
=
∂
∂z
az
1−m
∂
θ
∂z
(13.109)
For the soil a similar equation is valid:
∂T
g
∂t
= K
g
∂
2
T
g
∂z
2
(13.110)
These two equations have been the starting point of many investigations of the
calm nocturnal boundary layer. These two one-dimensional equations are coupled
by means of the interface condition
−ρ
g
c
g
K
g
∂T
g
∂z
=−a
ρc
p,0
z
1−m
∂
θ
∂z
+ R
N
,z= 0,t>0(13.111)

13.8 The Ekman layer – the classical approach 375
with R
N
= σT
4
S
−F
l
, a = 0.07 and m =
1
3
. In this equation vertical gradients must
be understood as limit statements. The radiative net flux at the ground is computed
with the help of some radiative-transfer model fully accounting for the presence of
absorbing and emitting gases. The reader will notice the internal inconsistency in
the system (13.111) since the derivation of (13.109) assumed that we have a dry
atmosphere that does not absorb and emit any infrared radiation. This imperfection
must be accepted if we wish to tackle the problem analytically. The solution of
this problem is not trivial by any means, but may be obtained with the help of
Laplace transforms. Omitting details, which may be found in Zdunkowski and
Kandelbinder (1997), here we just present the solution as
θ(z, t) =
θ
0
−
R
N
(n)
m/n
exp
−
z
n
2an
2
t
ρc
p,0
5
1
n
a
1/(2n)
z
1/2
∞
l=0
(−1)
l
δ
−(1+l)
t
α
W
−α,β
z
n
n
2
at
with α =
m + 2 + l(1 − m)
2n
,β=
m
2n
,n= m + 1
δ =
ρ
g
c
g
K
g
5
m
n
ρc
p,0
5
1
n
a
1/n
n
(1−m)/n
(13.112)
The potential temperature
θ
0
is the constant-height initial potential temperature.
The function W
α,β
(z) is the Whitaker function, which can be computed directly or
evaluated with the help of tables given in the Handbook of Mathematical Functions
by Abramowitz and Segun (1968). The change of the potential temperature with
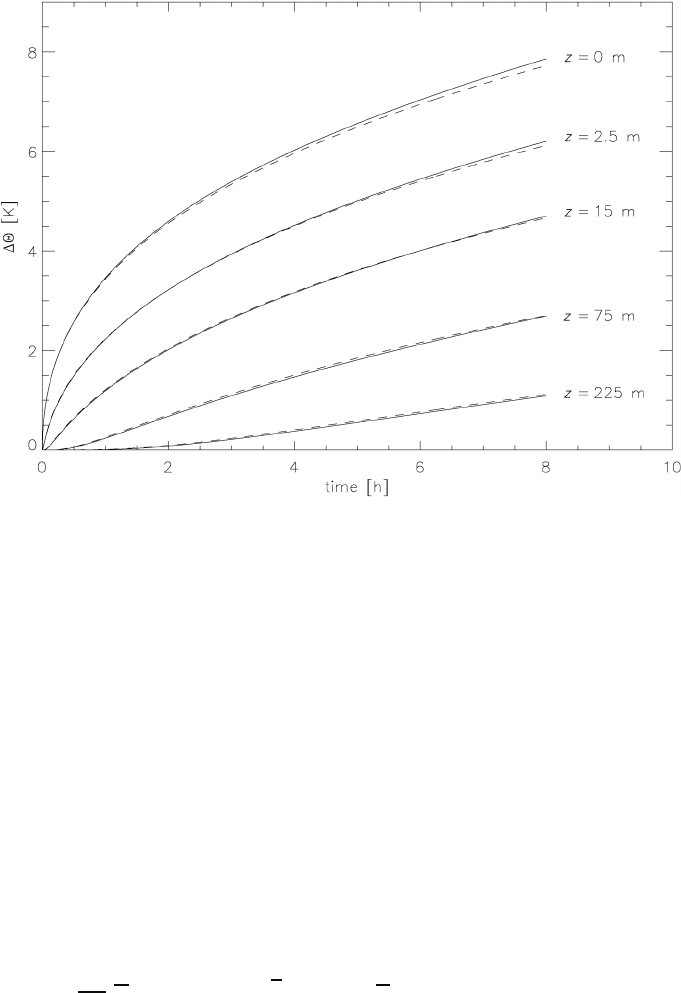
time after sunset is shown in Figure 13.5. A numerical model (discussed in the
original paper) is also used to show the influence of the radiative heating of the air,
which is very small. This justifies to some extent the dry-air assumption leading to
(13.109). Figure 13.5 shows that the cooling of the air is strongest near the earth’s
surface.
13.8 The Ekman layer – the classical approach
The major characteristics of the Ekman layer were listed in the introduction to
this chapter. Many successful numerical studies, too numerous to list here, were
performed in order to simulate the temperature and the wind fields of the entire
boundary layer. These studies were based on the use of different types of closure
assumptions to simulate the eddy exchange coefficient. Figure 13.6 shows a typical
height distribution of the exchange coefficient K after O’Brien (1970). In the lower
376 The atmospheric boundary layer
Fig. 13.5 Changes of the potential temperature with time counted from
sunset at various
heights with (dashed lines) and without (solid lines) radiative heating.
part of the boundary layer K increases more or less linearly with height until it
reaches a maximum value K
max
at h
1
.Aboveh
2
the exchange coefficient decreases
with height.
There is a region between the linear increase and the linear decrease where K
is approximately constant with height. The linear approximation of K shown in
Figure 13.6 will be used below to obtain an analytic solution of the wind field.
First we will present Taylor’s (1915) very simple analytic solution, which is based
on the assumption that the exchange coefficient is constant with height throughout
the entire boundary layer. The Taylor solution is already capable of capturing the
gross features of the wind profile in the Ekman layer.
The starting point of the analysis is the averaged equation of motion (11.35d):
D
Dt
(
ρ
v) +∇·(pE − J − R) =−ρ(∇φ + 2Ω ×
v)(13.113)
The theory considers only the mean horizontal motion, which is subjected to vari-
ous constraints in order to obtain a simple solution of the vertical wind profile. These
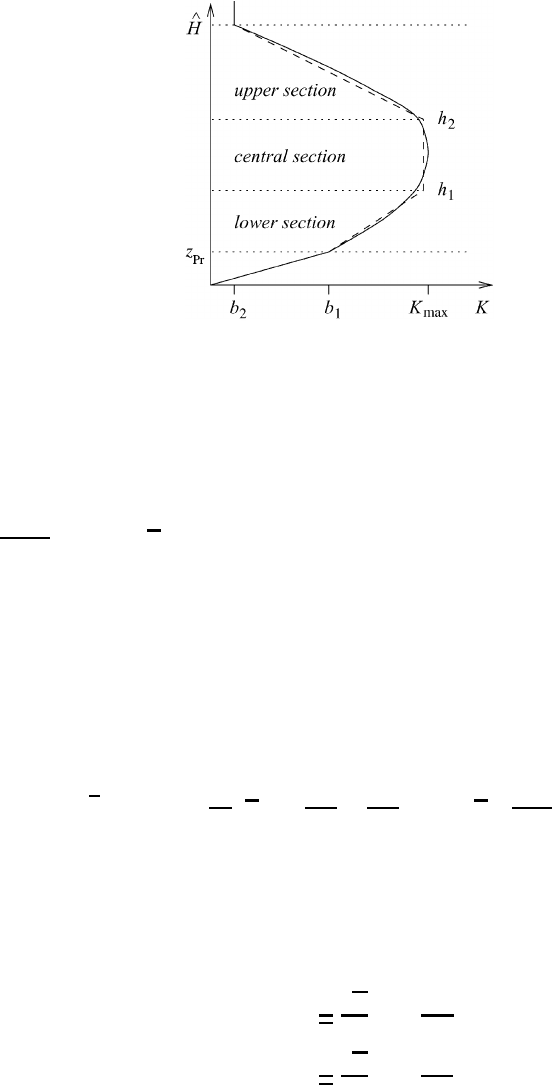
13.8 The Ekman layer – the classical approach 377
Fig. 13.6 Typical height variation of the exchange coefficient in the boundary layer (full
line) and the linear approximation (dashed line). At the top of the boundary layer a
residual
value is expected.
constraints are
d ...
dt
= 0,
ρ = constant,K
v
v
= K = constant,
v =
v
h
(z), w = 0
(13.114)
Thus the acceleration of the mean horizontal wind is zero while the density and
the exchange coefficient are independent of spatial coordinates. Moreover, it is
assumed that the geostrophic wind is independent of height and that the actual
wind becomes geostrophic as z approaches infinity. These assumptions imply that
the horizontal pressure gradient is constant with height also. Application of (11.92)
results in
∇·(
J + R) = i
3
·
∂
∂z
ρK
i
3
∂
v
h
∂z
+
∂
v
h
∂z
i
3
= ρK
∂
2
v
h
∂z
2
(13.115)
where
v
h
=ui +vj.
The equation of motion for the tangential plane (2.38) will now be modified
by including the conditions (13.114) and by adding frictional effects according to
(13.115). On replacing (u, v) by the average values (u,v)wefind
−f v =−
1
ρ
∂
p
∂x
+ K
∂
2
u
∂z
2
fu =−
1
ρ
∂
p
∂y
+ K
∂
2
v
∂z
2
(13.116)
378 The atmospheric boundary layer
As the next step we replace the components of the pressure-gradient force by the
corresponding components of the geostrophic wind:
u
g
=−
1
ρf
∂
p
∂y
,v
g
=
1
ρf
∂
p
∂x
,
since v
g
=
1
ρf
e
r
×∇
h
p
(13.117)
We choose our coordinate system in such a way that the pressure does not vary in
the x-direction so that v
g
vanishes. Substituting (13.117) into (13.116) gives the
following coupled system of second-order linear differential equations:
K
d
2
u
dz
2
=−fv, K
d
2
v
dz
2
= f (u − u
g
)(13.118)
Since z is the only independent variable, we have replaced the partial by the
total derivative. These two equations can be combined to give a single equation by
multiplying the second equation of (13.118) by
√
−1 = i and then adding the result
to the first equation. This gives the following second-order differential equation:
d
2
dz
2
(u + iv − u
g
) −
if
K
(u + iv − u
g
) = 0(13.119)
since the geostrophic wind was assumed to be height-independent. The general
solution of (13.119) is easily found by standard methods and is given by
u + iv − u
g
= C
1
exp
if
K
z
+ C
2
exp
−
if
K
z
= C
1
exp
f
2K
z
exp
i
f
2K
z
+ C
2
exp
−
f
2K
z
exp
−i
f
2K
z
(13.120)
since
√
i = (1 +i)/
√
2. Application of the boundary conditions at z = 0, u +iv =
0, and at z −→ ∞, u + iv = u
g
, gives the required integration constants C
1
= 0
and C
2
=−u
g
, and (13.120) results in
u + iv = u
g
{1 − exp(−Az)[cos(Az) − i sin(Az)]} with A =
f
2K
(13.121)
13.8 The Ekman layer – the classical approach 379
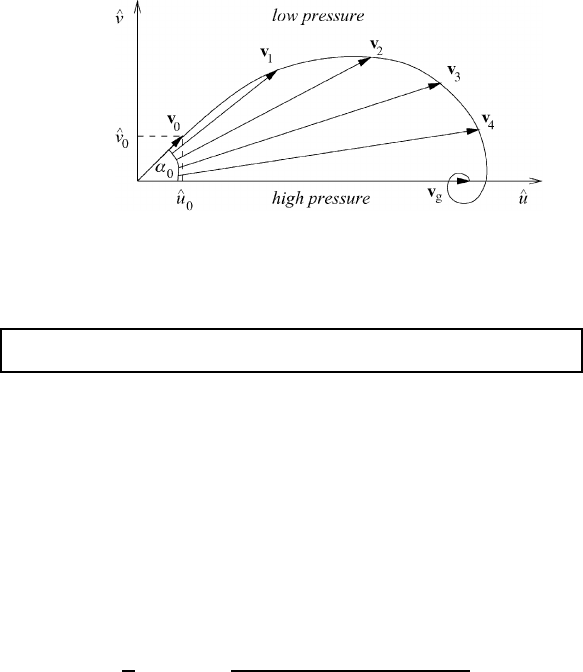
Fig. 13.7 The Ekman spiral, showing turning of the wind vector with height.
The solution may be separated by comparing the real and imaginary parts:
u = u
g
1 − exp(−Az)cos(Az)
, v = u
g
exp(−Az)sin(Az) (13.122)
Taking v as the ordinate and u as the abscissa we obtain a nomogram, which is
displayed in Figure 13.7. This nomogram is the celebrated Ekman spiral showing
that the wind vector is turning clockwise in the northern hemisphere. For various
heights the horizontal wind vector is shown, indicating that, with increasing height,
the horizontal wind approaches the geostrophic wind. The largest cross-isobar
angle α
0
is found at the earth’s surface. α
0
can be found from the ratio of the
wind-vector components. For z = 0 this gives an indeterminant form 0/0. By
using (13.122) and applying L’Hospital’s rule we find
tan α
0
= lim
z→0
v
u
= lim
z→0
u
g
exp(−Az)sin(Az)
u
g
1 − exp(−Az)cos(Az)
= 1 =⇒ α
0
= 45
◦
(13.123)
This value is too large and does not agree with observations. The height at which
the actual wind coincides for the first time with the direction of the geostrophic
wind is known as the geostrophic wind height z
g
. There the wind speed exceeds
the geostrophic wind by a few percent. The height of the planetary boundary layer
is often defined by z
g
. From the condition v(z
g
) = 0, implying that Az
g
= π,we
find the height of the boundary layer as
z
g
= π/A (13.124)
Assuming that K = 5m
2
s
−1
, which is a reasonable midlatitude value, and f =
10
−4
s
−1
we find that z
g
= 1000 m. For different values of K this height may be
twice as large or just half as large.
We will now investigate the influence of the turbulent viscosity, represented by
the eddy exchange coefficient K, on the Ekman profile more closely. Applying the

380 The atmospheric boundary layer
general definition (13.9) of the stress vector to equation (11.92), assuming that the
exchange coefficient is constant with height, we find
T = i
3
· (J + R) = ρK
∂
v
h
∂z
=⇒
1
ρ
∂T
∂z
= K
∂
2
v
h
∂z
2
(13.125)
The second equation follows immediately since the density was assumed to be
constant with height. This expression is the frictional force per unit mass due to the
eddy viscosity of the air. Equation (13.116) can be written in the following form:
−
ρK
∂
2
v
h
∂z
2
=−∇
h
p − ρf i
3
×
v
h
(13.126)
To eliminate the pressure gradient we use the definition of the geostrophic wind
(13.117). Taking the cross product i
3
× v
g
and applying the Grassmann rule, we
obtain immediately
i
3
× v
g
=
1
ρf
i
3
× (i
3
×∇
h
p) =−
1
ρf
∇
h
p (13.127)
Substitution of this expression into (13.126) yields
K
∂
2
v
h
∂z
2
= f i
3
× (
v
h
− v
g
)(13.128)
which can be easily interpreted with the help of Figure 13.8. The vectorial difference
=
v
h
=
v
h
− v
g
between the horizontal and the geostrophic wind vectors is known
as the geostrophic wind deviation. The Coriolis force is perpendicular to the actual
wind vector and the pressure gradient force is perpendicular to the geostrophic
wind vector. By adding the frictional force we obtain the balance of forces. The
frictional force is perpendicular to the geostrophic deviation. The magnitude of the
geostrophic deviation decreases with height and is zero at the top of the boundary
layer since the frictional force vanishes at the level z
g
.
Fig. 13.8 The balance of forces for unaccelerated flow in the Ekman layer.
