Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

11.8 Production of entropy in the microturbulent system 321
into (11.77) results in the entropy-production equation
T Q
s
=−µ
n
I
n
−
(J
h
+ J
h
t
) −
h
n
(J
n
+ J
n
t
)
·
∇T
T
− (
J
n
+ J
n
t
) · (∇µ
n
)
T
+ J
θ
t
·∇ln
( + ! ≥ 0
(11.79)
with
! = J··∇
v
A
+ J··∇v
. By introducing the sensible enthalpy fluxes we obtain
the final form of the entropy production:
T Q
s
=−µ
n
I
n
− (J
h
s
+ J
h
s,t
) ·∇ln T
− (
J
n
+ J
n
t
) · (∇µ
n
)
T
+ J
θ
t
·∇ln
( + ! ≥ 0
(11.80)
We assume that Curie’s principle, as explained in TH and elsewhere, also applies
to turbulent systems. This permits us to split the total entropy production into parts.
Each part belongs to a certain tensorial class (scalar, vectorial, and dyadic) and
is required to be positive definite. Thus, the scalar part of the entropy production
containing the phase-transition fluxes and the energy dissipation is given by
−µ
n
I
n
+ ! ≥ 0(11.81)
For the vectorial part we may write
−(
J
h
s
+ J
h
s,t
) ·∇ln T − (J
n
+ J
n
t
) · (∇µ
n
)
T
+ J
θ
t
·∇ln
( ≥ 0(11.82)
We will now attempt to parameterize the various fluxes. The parameterization
of the mean energy dissipation
! is best left to the statistical theory of turbulence.
Review of (11.35d) and of (11.45) shows that the equation of motion and the
equation of the kinetic energy of the mean flow contain the sum of the mean
molecular and turbulent momentum fluxes. These fluxes cannot be found with the
help (11.80) since they do not appear in this particular version of the entropy-
production equation. The treatment of these fluxes would require an entropy-
production equation in a different but equivalent form. It turns out, however, that
the determination of the dyadic fluxes would be a rather involved mathematical
process. For this reason we will treat the dyadic fluxes in an approximate manner,
which will be sufficient for our purposes.
In order to determine the fluxes we should involve the full linear Onsager theory.
However, the numerical evaluation of the resulting fluxes as part of prognostic
models would be prohibitively expensive in computer expenditure now and for
some time to come. Therefore, we will make some simplifying assumptions.

322 Turbulent systems
11.8.1 Scalar fluxes
Every scalar flux is driven only by its conjugated thermodynamic force, thus
ignoring all superpositions. The thermodynamic force for the phase-transitions
is the so-called chemical affinity a
k1
= µ
k
− µ
1
. To obtain the phase-transition
rate, the a
k1
must be multiplied by the phenomenological coefficients l
(k)
.The
phase-transition fluxes are then given by
I
0
= 0, I
1
=−I
2
− I
3
, I
2
=−l
(2)
a
21
, I
3
=−l
(3)
a
31
l
(2)
≥ 0,l
(3)
≥ 0, a
21
= (µ
2
−µ
1
), a
31
= (µ
3
−µ
1
)
(11.83)
The chemical affinities a
21
and a
31
refer to the phase transitions between liquid
water and water vapor and between ice and water vapor, respectively. The phe-
nomenological coefficients should be evaluated in terms of average values of the
state variables.
11.8.2 Vectorial fluxes
Again we assume that superpositions are excluded. First we rewrite the inequality
(11.82). This treatment is motivated by the fact that the potential temperature is
nearly conserved in many atmospheric processes so that the turbulent flux J
θ
t
is
expected to be driven by the gradient of the potential temperature. We replace J
h
s,t
according to (11.69), thus obtaining a different arrangement of fluxes and their
thermodynamic forces:
−(
J
h
s
+ J
(
t
) ·∇ln T − (J
n
+ J
n
t
) · (∇µ
n
)
T
− J
θ
t
·∇ln
θ ≥ 0(11.84)
Now the flux J
θ
t
is driven by the gradient of the potential temperature as desired.
In order to guarantee that this inequality is satisfied, each flux must be propor-
tional to the thermodynamic force driving the flux. To make sure that each mea-
sure number of the flux depends on each measure number of the thermodynamic
forces, we introduce dyadic phenomenological coefficients. The coefficient matrix
representing the dyadic coefficient, according to the linear Onsager theory, must be
symmetric. The vectorial fluxes are then given by the following set of equations:
(a) J
θ
t
=−B
θ
·∇ln
θ =−ρ c
p
K
θ
·∇
θ, B
θ
= ρ c
p
θK
θ
(b) J
h
s
+ J
(
t
=−B
T
·∇ln T =−ρ c
p
K
T
·∇T, B
T
=−ρ c
p
T K
T
(c) J
k
+ J
k
t
=−B
k
·∇(µ
k
−µ
0
)
T
,k= 1, 2, 3
(11.85)
In order to evaluate (11.85c) we use the identity
∇(µ
k
−µ
0
)
T
=
∂
∂p
(µ
k
−µ
0
) ∇p +
∂
∂m
n
(µ
k
−µ
0
) ∇m
n
(11.86)

11.8 Production of entropy in the microturbulent system 323
The various K appearing in (11.85) are known as the exchange dyadics.Itisvery
difficult to evaluate the turbulent flux J
(
t
in (11.85b), which is often considered to
be negligibly small. Since the mean molecular sensible heat flux is also of a very
small magnitude in comparison with J
θ
t
, equation (11.85b) is often totally ignored.
It should be clearly understood that the fluxes appearing in (11.85) cannot be
considered as fully parameterized since we did not show how the elements of the
matrices representing the various
B can be calculated. In fact, the determination
of these elements is very difficult and we will have to be satisfied with several
approximations.
Finally, we are going to assume that the tensor ellipsoids characterizing the state
of atmospheric turbulence are rotational ellipsoids about the z-axis. In this case
each symmetric dyadic in the x, y,z system is described by only two measure
numbers. In the general case we need nine coefficients. With the assumption of
rotational symmetry, the phenomenological equations assume a simplified form.
Since we are going to use the Cartesian system, we must also use the corresponding
unit vectors (i
1
, i
2
, i
3
).
11.8.3 The scalar phenomenological equations
The scalar phase-transition fluxes given by equation (11.83) are not affected by the
above assumption and retain their validity.
11.8.4 The vectorial phenomenological equations
The symmetric coefficient dyadics
B are represented by two measure numbers only.
Omitting any superscripts, we may write this dyadic as
B = B
h
(i
1
i
1
+ i
2
i
2
) + B
v
i
3
i
3
(11.87)
where B
h
and B
v
represent the horizontal and vertical measure numbers. With this
simplified representation of the exchange dyadic the vectorial fluxes assume the
simplified forms
(a) J
θ
t
=−ρ c
p
K
θ
h
(i
1
i
1
+ i
2
i
2
) + K
θ
v
i
3
i
3
·∇
θ
(b) J
h
s
+ J
(
t
=−ρ c
p
K
T
h
(i
1
i
1
+ i
2
i
2
) + K
T
v
i
3
i
3
·∇T
(c)
J
k
+ J
k
t
=−ρ
K
k
h
(i
1
i
1
+ i
2
i
2
) + K
k
v
i
3
i
3
·∇(µ
k
−µ
0
)
T
(11.88)
The factors K
h
and K
v
are known as exchange coefficients.
324 Turbulent systems
11.8.5 The dyadic fluxes
As has previously been stated, the sum of the fluxes
J + R cannot be dealt with in
terms of the entropy production (11.80) since they do not appear in this equation. We
will now give a form for these dyadic fluxes that is acceptable for many situations
by assuming that the molecular and turbulent fluxes can be stated in analogous
forms. For the molecular system we have
J = µ(∇v
A
+ v
A
∇) −
2
3
µ − l
11
∇·v
A
E (11.89)
In the following we will assume that the divergence term may be neglected. It
seems logical to parameterize the fluxes for the turbulent system by replacing the
velocity v
A
by the average
v
A
. In this case we may first write
∇
v
A
+
v
A
∇=
∇
h
+ i
3
∂
∂z
(
v
A,h
+ i
3
w
A
) + (
v
A,h
+ i
3
w
A
)
∇
h
+ i
3
∂
∂z
(11.90)
Assuming additionaly that w
A
= 0, we find
∇
v
A
+
v
A
∇=∇
h
v
A,h
+
v
A,h
∇
h
+ i
3
∂
v
A,h
∂z
+
∂
v
A,h
∂z
i
3
(11.91)
By using only two turbulence coefficients, K
v
h
≥ 0andK
v
v
≥ 0, we find the
approximate expression
J + R = ρK
v
h
(∇
h
v
A,h
+
v
A,h
∇
h
) + ρK
v
v
i
3
∂
v
A,h
∂z
+
∂
v
A,h
∂z
i
3
(11.92)
It should be clearly understood that the steps leading to (11.91) are not part of a
rigorous derivation. The equations obtained in this section will be used in a later
chapter when we are dealing with the physics of the atmospheric boundary layer.
11.9 Problems
11.1: Verify the validity of equations (11.7), (11.18), and (11.19).
11.2: Show that the interchange rule (11.25) applies to the microturbulent system.
11.3: Verify the validity of
−p ∇·v
A
=−p ∇·
v
A
− ∇·(pv
) + v
·∇p
11.9 Problems 325
11.4: Verify the first and the last equation of (11.42).
11.5: Perform the necessary operations to obtain equation (11.45) from (11.35d).
11.6: Show that
3
k=0
I
k
= 0
11.7: Show that
D
Dt
(
ρ
k) =−∇·k
t
+ ρv
·
dv
dt
+∇
v
2
2
with
k =
v
2
2
and k
t
= ρv
v
2
2
11.8: Inspection of equation (11.33) seems to indicate that the divergence of the
term J
e
t
= ρev
should appear in (11.48) instead of the turbulent enthalpy flux J
h
t
.
By developing the expression −p ∇·v
A
show that the appearence of the turbulent
enthalpy flux is correct.
12
An excursion into spectral turbulence theory
The phenomenological theory discussed in the previous chapter did not permit
the parameterization of the energy dissipation. In this chapter spectral turbulence
theory will be presented to the extent that we appreciate the connections among
the turbulent exchange coefficient, the energy dissipation, and the turbulent kinetic
energy. In the spectral representation we think of the longer waves as the averaged
quantities and the short waves as the turbulent fluctuations. Since the system of
atmospheric prediction equations is very complicated we will be compelled to
apply some simplifications.
12.1 Fourier representation of the continuity equation
and the equation of motion
Before we begin with the actual transformation it may be useful to briefly review
some basic concepts. For this reason let us consider the function a(x) which has
been defined on the interval L only. In order to represent the function by a Fourier
series, we extend it by assuming spatial periodicity. Using Cartesian coordinates
we obtain a plot as exemplified in Figure 12.1. The period L is taken to be large
enough that averaged quantities within L may vary, i.e. the averaging interval
x L.
Certain conditions must be imposed on a(x) in order to make the expansion
valid. The function a(x) must be a bounded periodic function that in any one
period has at most a finite number of local maxima and minima and a finite number
of points of discontinuity. If these conditions are met then the Fourier expansion of
a(x) converges to the function a(x) at all points where the function is continuous
and to the average of the right-hand and left-hand limits at each point where a(x)
is discontinuous. These are the Dirichlet conditions which are usually met in
326
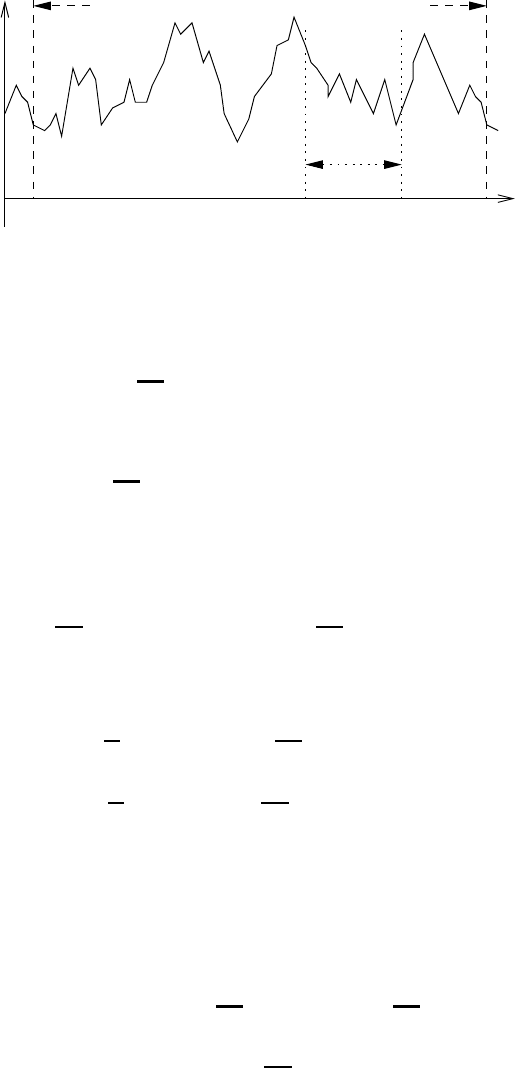
12.1 Fourier representation 327
L
x
x
a(x)
Fig. 12.1 The function a(x) and its periodic extension. L is the period and x the
averaging interval.
meteorological analysis. The Fourier expansion of a(x)isgivenby
a(x) =
∞
l=−∞
A(l)exp
i
2π
L
lx
,l= ...,−2, −1, 0, 1, 2,... (12.1)
or, using the summation convention, by
a(x) = A(n)exp
i
2π
L
nx
,n= ...,−2, −1, 0, 1, 2,... (12.2)
In order to obtain the amplitude A(k), we multiply (12.2) by the factor
exp[−i(2π/L)kx] and integrate the resulting expression over the expansion in-
terval L. This results in
L
0
a(x)exp
−i
2π
L
kx
dx = A(n)
L
0
exp
i
2π
L
(n − k)x
dx = δ
k
n
LA(n)
(12.3)
so that the amplitude and its conjugate are given by
A(k) =
1
L
L
0
a(x)exp
−i
2π
L
kx
dx,
A(k) =
1
L
L
0
a(x)exp
i
2π
L
kx
dx=A(−k)
(12.4)
A schematic representation of the first three waves is shown in Figure 12.2, together
with the corresponding amplitudes. It will be recognized that a large value of l refers
to short waves whereas a small value signifies longer waves.
We will now obtain a useful mathematical expression that will be helpful in our
work. We first multiply the functions a(x)andb(x) and their expansions, yielding
a(x)b(x) = A(n)exp
i
2π
L
nx
B(m)exp
i
2π
L
mx
= A(n)B(m)exp
i
2π
L
(n + m)x
(12.5a)
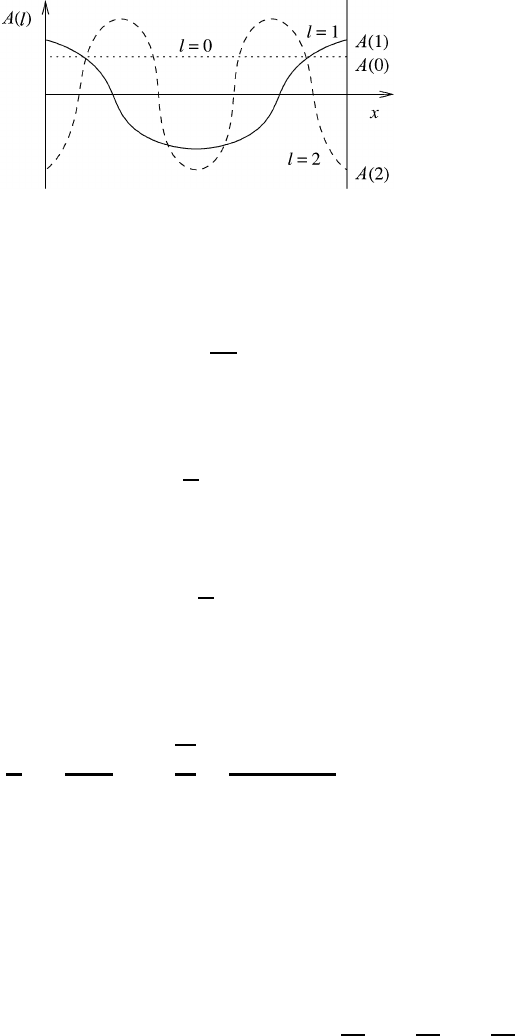
328 An excursion into spectral turbulence theory
Fig. 12.2 A schematic representation of the first three waves in the interval L and the
corresponding amplitudes.
On integrating this expression over the expansion interval we immediately find
L
0
a(x)b(x) dx = A(n)B(m)
L
0
exp
i
2π
L
(n + m)x
dx = A(n)B(m)δ
0
n+m
L
(12.5b)
From the Kronecker symbol it follows that m =−n,sothat
A(n)B(−n) =
1
L
L
0
a(x)b(x) dx (12.5c)
For the special case A = B we obtain
A(n)A(−n) =
1
L
L
0
a
2
(x) dx (12.6)
which is known as Parseval’s identity for Fourier series; summation over n is
implied. Obviously this expression is real. For example, let the function a(x)
represent the velocity component u(x). In this case we obtain
1
L
L
0
u
2
(x)
2
dx =
u
2
2
=
U(n)U(−n)
2
= E
u
(12.7)
representing the average value of the kinetic energy per unit mass.
We will now generalize the previous treatment to three dimensions and formally
admit the time dependency of the function a. Now the interval of expansion changes
to the volume of expansion as shown in Figure 12.3. In analogy to the one-
dimensional case, periodicity is now required for the volume.
The formal expansion is then given by
a(x
1
,x
2
,x
3
,t) =
∞
l
1
=−∞
∞
l
2
=−∞
∞
l
3
=−∞
A(l
1
,l
2
,l
3
,t)exp
i2π
l
1
L
1
x
1
+
l
2
L
2
x
2
+
l
3
L
3
x
3
(12.8)
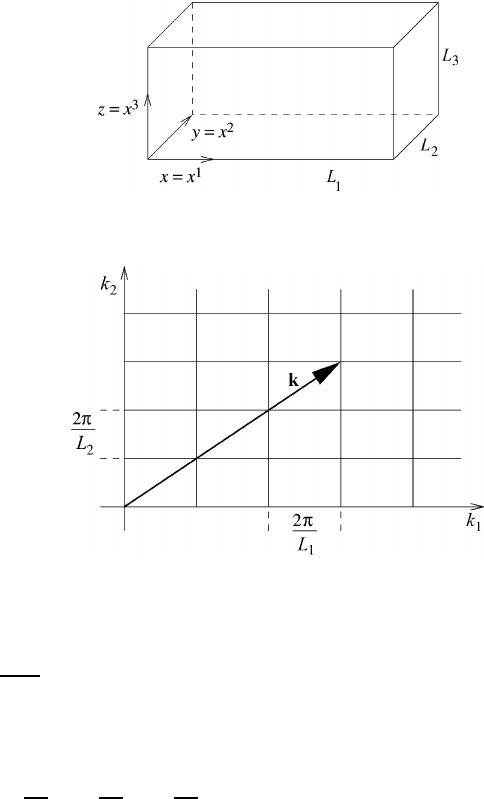
12.1 Fourier representation 329
Fig. 12.3 The expansion volume V = L
1
L
2
L
3
for the function a(x
1
,x
2
,x
3
,t).
Fig. 12.4 A schematic representation of the wavenumber vector in the plane.
We now introduce the abbreviations
k
i
=
2πl
i
L
i
, r = i
1
x
1
+ i
2
x
2
+ i
3
x
3
, k = i
1
k
1
+ i
2
k
2
+ i
3
k
3
(12.9a)
where the third equation represents the wavenumber vector. The exponent in (12.8)
can then be written as the scalar product:
2π
l
1
L
1
x
1
+
l
2
L
2
x
2
+
l
3
L
3
x
3
= k
1
x
1
+ k
2
x
2
+ k
3
x
3
= k ·r (12.9b)
To simplify the notation we formally introduce the summation wavenumber
vector k
k
=
∞
l
1
=−∞
∞
l
2
=−∞
∞
l
3
=−∞
(12.9c)
and obtain the representation
a(r,t) =
k
A(k,t) exp(ik · r) = A(n,t) exp(in · r)(12.9d)
Figure 12.4 shows a schematic representation of the wavenumber vector in the
plane.

330 An excursion into spectral turbulence theory
As stated at the beginning of this chapter, we need to simplify the physical–
mathematical system in order to make the analysis more tractable. First of all we
postulate a dry constant-density atmosphere, that is α = 1/ρ = constant, resulting
in a simplified continuity equation. Expanding the velocity vector according to
(12.9d) we may write
v(r,t) = V(n,t) exp(in · r)(12.10)
so that the continuity equation can be expressed as
∇·v = V(n,t) ·∇exp(in · r) = 0(12.11)
The gradient operator acting on the exponential part with wavenumber vector k
results in
∇ exp(ik ·r) = exp(ik ·r) ∇(ik ·r) = i exp(ik ·r) ∇r ·k = ik exp(ik ·r)(12.12)
It is now convenient to write the Laplacian of the exponential part as
∇
2
exp(ik ·r) =∇·∇exp(ik · r) =−k
2
exp(ik ·r)(12.13)
since this expression will be needed soon. Using (12.12), the continuity equation
assumes the form
V(n,t) · ni exp(in ·r) = 0(12.14)
Since this expression must hold for every wavenumber vector k, the expression
V(k,t) · k = 0, k ⊥ V(k,t)(12.15)
is also true, thus proving that the velocity amplitude V(k,t) is perpendicular to the
wavenumber vector k.
Our next task is to write the equation of motion in the spectral form. By ignoring
the Coriolis force the equation of motion may be written as
∂v
∂t
+∇·(vv) =−∇ +
1
ρ
∇·
J (12.16)
Here the abbreviation = αp +φ has been used. Previously the same symbol re-
presented the Exner function, but confusion is unlikely to arise. Since the divergence
of the velocity is zero the stress tensor
J reduces to the simplified form
J = µ(∇v + v
∇) =⇒
1
ρ
∇·
J = ν ∇
2
v,ν=
µ
ρ
(12.17)
