Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

10.4 Frictionless baroclinic ﬂow 291

␣

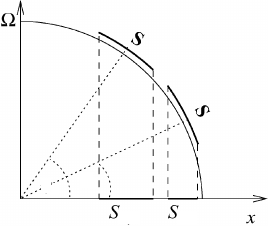
Fig. 10.4 The solenoidal effect.

In (M6.27) the validity of the following equation was shown:



∇p ×∇α · dS =



dp dα (10.118)

The right-hand side of this equation represents the number N(α, −p) of solenoids

contained within the integration surface S.InthetermN (α, −p) pressure is given

a negative sign since p decreases but α increases with height. Comparison of

(10.118) with (10.117) shows that the number of solenoids may also be expressed

in a temperature and entropy coordinate system.

In the absence of friction we may now write the Bjerkness circulation theorem

in the form

=−2$

+ N (α, −p)

(10.119)

The solenoidal term produces a direct circulation, as will be recognized from

Figure 10.4.

We will now explain the meaning of the ﬁrst term on the right-hand side of

(10.119). This term results from the Coriolis effect. If a material surface expands

in time its projection onto the equatorial plane increases. As a consequence an

existing cyclonic circulation (C>0) weakens whereas an anticyclonic circulation

(C<0) intensiﬁes. If the material surface contracts the opposite effects take place.

Let us consider a closed material curve along a latitude circle that is displaced

toward the north pole. This results in an intensiﬁcation of the westerlies, whereas

a displacement toward the equator has the opposite effect.

Next we consider the displacement of a material surface not enclosing the ro-

tational axis of the earth; see Figure 10.5. This surface is oriented nearly parallel

292 Circulation and vorticity theorems

␸

E,2

E,1

Fig. 10.5 The latitudinal effect.

to the earth’s surface. A poleward displacement increases the projection onto the

equatorial plane so that a cyclonic circulation along the enclosed surface is weak-

ened whereas an existing anticyclonic circulation is intensiﬁed. A displacement

toward the equator has the opposite effect. The change of the circulation due to

a latitudinal displacement is known as the latitudinal effect. The convergence or

divergence of the ﬂow ﬁeld resulting in an contraction or expansion of the material

surfaces is known as the divergence effect. In summary, expansion (contraction)

of the material surface and poleward (southward) motion work in the same di-

rection. The combination of displacement with contraction or expansion may also

occur.

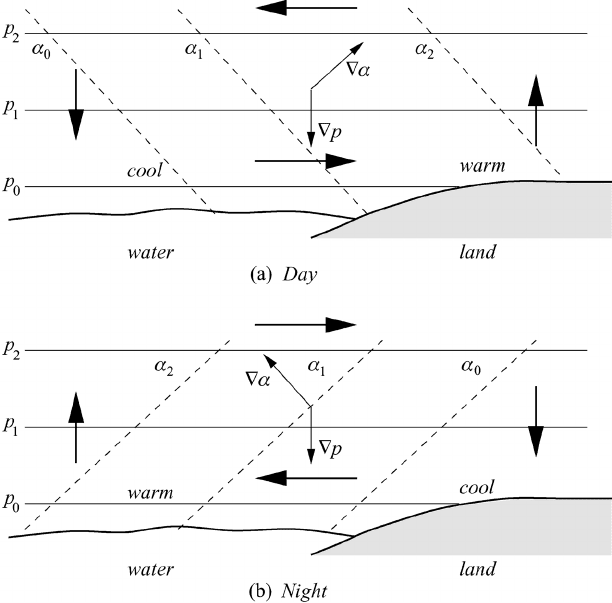
On the small spatial scales of land–sea breezes and mountain–valley winds the

rotational effect of the earth may be disregarded. The observed circulation pat-

tern is then solely due to the solenoidal effect. On this small scale the isobaric

surfaces may be considered horizontal, see Figure 10.6, in which the circulation

patterns for the land-and-sea breeze are shown for a calm and cloudless summer

situation. During the day the land is heated while the water surface remains rel-

atively cool. The isosteric surfaces then assume the orientation depicted, causing

the wind to blow from the sea toward the land. This is shown by the direction

of the solenoidal vector. During the night the opposite situation occurs. The land

surface cools off and the water remains relatively warm so that the wind blows

from the land toward the sea. This type of circulation takes place on a relatively

small scale. Even in well developed situations the scales of the motion hardly

exceed a few hundred meters in the vertical direction and about 80 km in the hori-

zontal direction if large bodies of water are involved. A similar situation develops

for mountain and valley breezes, for which the slopes are heated more rapidly

than the air during daytime and cooled more strongly than the air during the

night.

10.5 Frictionless barotropic ﬂow 293

Fig. 10.6 Representation of a land-and-sea breeze circulation.

10.5 Circulation and vorticity theorems for frictionless barotropic ﬂow

10.5.1 The barotropic Ertel–Rossby invariant

A barotropic ﬂuid is characterized by the condition N = 0. This implies that isobaric

and isosteric surfaces are parallel so that solenoids cannot form. Whenever we deal

with a barotropic ﬂuid we effectively ignore the laws of thermodynamics since the

speciﬁc volume is a function of pressure only. Therefore, we cannot proceed as

before to eliminate the pressure gradient in terms of enthalpy, temperature, and

entropy. Instead of this, we leave the equation of absolute motion in the original

form, but we replace the pressure gradient force by

α ∇p =∇





αdp



(10.120)

The proof of this formula is left as an exercise. Now the equation of motion of the

294 Circulation and vorticity theorems

absolute system reduces to

=−∇





αdp



(10.121)

By comparison of (10.121) with the baroclinic form of the equation of motion

(10.21) and retracing the steps leading to (10.24), we ﬁnd the barotropic form of

the equation of motion in Lagrangian coordinates:

∂x

∂a



∂

∂t



=−

∂

∂a





αdp



(10.122)

Inspection of the mathematical steps involved in going from (10.24) to (10.28)

reveals that, in the barotropic case, the Lagrangian function is given by

− φ

−



αdp (10.123)

so that the action integral W

now reads

∗





− φ

−



αdp



dt (10.124)

The star denotes the barotropic system. Instead of (10.43), the Weber transformation

is now given by

∗

= v

−∇W

∗

, ∇×B

∗

=∇×v

(10.125)

The transition from the baroclinic to the barotropic vortex laws may be accom-

plished by replacing B

by B

∗

In the barotropic atmosphere the baroclinic Ertel–Rossby conservation law

(10.48) of the absolute system reduces to



α(v

−∇W

∗

) ·∇×v



= 0

(10.126)

where

∗

= α(v

−∇W

∗

) ·∇×v

(10.127)

is the barotropic Ertel–Rossby invariant.Ifv

is replaced by v + v

then the

theorem refers to relative motion.

10.5 Frictionless barotropic ﬂow 295

10.5.2 Barotropic vortex theorems of Ertel, Helmholtz, and Thomson

Owing to the condition of barotropy ∇α ×∇p = 0, the right-hand side of (10.61)

vanishes. If the arbitrary ﬁeld function ψ = s and we assume that changes of state

are isentropic (ds/dt = 0), Ertel’s vortex theorem reduces to

(α ∇×v

·∇s) = 0

(10.128)

This expression is formally identical to the corresponding conservation law (10.63)

of the baroclinic system.

In order to obtain the Helmholtz vortex theorem for the absolute system in a

barotropic atmosphere we again replace B

by B

∗

. Instead of (10.98) we obtain

for frictionless motion

(∇×v

) =∇×v

·∇v

−∇·v

(∇×v

)

(10.129)

On repeating the arguments of Section 10.4.6 we see that ∇×v

remains zero if

it is zero at time t = 0. The transition to the relative system is accomplished by

replacing v

by v + v

Thomson’s barotropic circulation theorem is an integral statement of the

Helmholtz barotropic vortex theorem and can be derived in the same manner

as its baroclinic counterpart. More easily we ﬁnd it from Thomson’s baroclinic

circulation theorem if B

is replaced by B

∗

in (10.108). This yields





∗

· dr







· dr



−





∗



= 0(10.130)

The closed line integral of an exact differential is zero, so the last term vanishes. On

substituting the deﬁnition of the absolute circulation from (10.109) and applying

Stokes’ integral theorem, we ﬁnd





∇×v

· dS







· dr



= 0 (10.131)

The physical content of this equation is that the absolute circulation along the

closed material curve 6 is a constant. This theorem has a number of important

consequences, which will now be discussed in some detail.

296 Circulation and vorticity theorems

10.5.3 Vortex lines and vortex tubes

Vortex lines may be introduced analogously to streamlines, which are deﬁned by

the differential equation (3.39). Thus vortex lines are deﬁned by

dr × (∇×v

) = 0(10.132)

representing curves whose tangents are parallel to the vorticity vector ∇×v

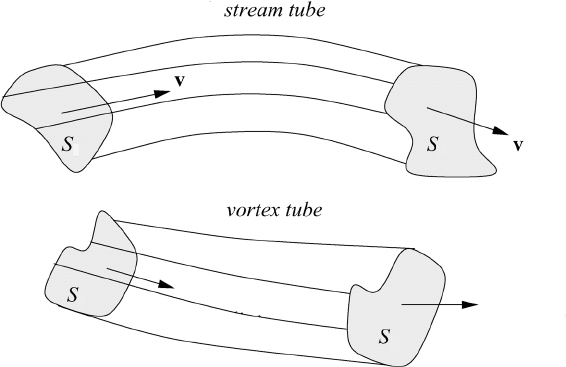
Before we introduce the idea of a vortex tube we consider the concept of a stream

tube. The deﬁnition of a streamline may be extended to a stream tube whose side

walls are composed of streamlines. For any closed contour in a ﬂow ﬁeld each

point on the contour will have a streamline passing through it. By considering

all points on the contour an inﬁnite number of streamlines is obtained, forming a

surface known as a stream tube. Figure 10.7(a) shows a section of a stream tube

deﬁned by a contour enclosing the surface S

. The corresponding contour a small

distance away encloses the surface S

. If the cross-section of the stream tube is

inﬁnitesimally small it is called a stream ﬁlament.

The deﬁnition of a vortex tube is analogous to that of a stream tube. Any point

on a closed contour in the ﬂow ﬁeld will have a vortex line passing through it,

thus forming a vortex tube. If the contour encloses the surface area S we obtain

the conﬁguration as shown in Figure 10.7(b). A vortex tube whose cross-section is

inﬁnitesimally small is known as a vortex ﬁlament.

(∇

⫻

)

(∇ ⫻ v

)

A,2

A,1

(b)

(a)

Fig. 10.7 Stream tubes and vortex tubes.

10.5 Frictionless barotropic ﬂow 297

Some very interesting properties of the ﬂow ﬁeld can be derived from the fact

that the divergence of the curl of any vector vanishes. Applying this to the vector

ﬁeld v

,wehave

∇·(∇×v

) = 0(10.133)

Since the vorticity vector is divergence-free there can be no sources and sinks of

the vorticity in the ﬂuid itself. This means that vortex lines either form closed

loops or must terminate on the boundary of the ﬂuid, which may either be a solid

surface or a free surface. Because the vorticity vector is divergence-free, we have

an analogy with the ﬂow of an incompressible ﬂuid whose continuity equation is

∇·v

= 0, showing that the velocity vector v

is divergence-free. Integration of

this expression over the closed surface of the stream tube V

or stream ﬁlament

gives



∇·v

dτ =



· dS = 0(10.134)

The surface-element vector dS is orthogonal to the side walls of the stream tube or

to v

, so the side walls cannot make a contribution to the surface integral. Therefore,

(10.134) reduces to



· dS +



· dS = 0(10.135)

Since dS, by deﬁnition, is always pointing in the direction of the outward normal,

we may deﬁne the ﬂow rate with respect to surfaces S

and S

by means of



· dS =−F



· dS = F

(10.136)

= F

(10.137)

as follows from (10.135). Divergence-free ﬂow of the velocity vector results in

equal ﬂow rates for the ﬂuid crossing S

and S

We now integrate (10.133) over the volume and obtain in complete analogy to

(10.134) the expression



∇·∇×v

dτ =



∇×v

· dS = 0(10.138)

Since ∇×v

· dS = 0 on the walls of the vortex tube, we have



∇×v

· dS +



∇×v

· dS = 0(10.139)

298 Circulation and vorticity theorems

Application of Stokes’ integral theorem gives



∇×v

· dS =



· dr =−C



∇×v

· dS =



· dr = C

(10.140)

or, from (10.139),

= C

(10.141)

This simple statement shows that the absolute circulations around the limiting

contours of surfaces S

and S

are identical. Alternately we may say that the

circulation through each cross-sectional area is the same. Comparison of (10.137)

and (10.141) shows that, in case of the stream tube, the ﬂow rates at S

and S

are

equal while the absolute circulation along the vortex tube is the same.

Equation (10.139) can also be interpreted in a different manner. If the cross-

sectional area S of the vortex tube is sufﬁciently small, we may deﬁne a meaningful

average vorticity by means of



∇×v

· dS



= ∇×v







∇×v



S (10.142)

This expression is known as the vortex strength. With reference to (10.139) and

(10.140) we ﬁnd for the ﬂow through cross-sections S

and S

the expression



∇×v



∇×v



(10.143)

stating that the vortex strength is constant along the vortex tube. From the fact

that the vorticity vector is divergence-free it follows that vortex tubes must be

closed, terminate on a solid boundary, or terminate on a free surface. Observational

evidence for closed vortex tubes is provided by smoke rings, whereas a vortex tube

at a free surface ﬂow may have one end at the free surface and the other end at the

solid boundary of the ﬂuid.

Additional information on the kinematics of vortex tubes may be obtained by

considering a closed curve 6 located entirely on the side wall of the vortex tube

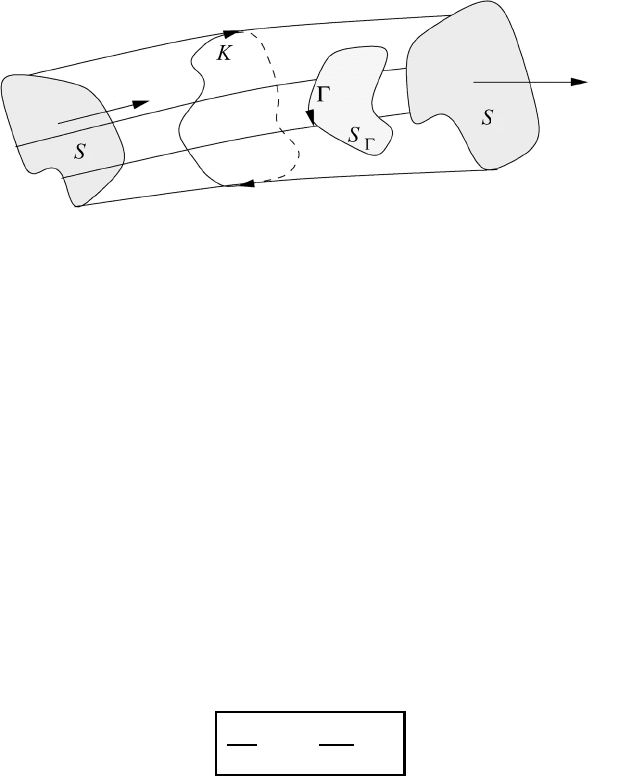
which does not enclose the axis of the vortex tube; see Figure 10.8.

Since ∇×v

is perpendicular to dS we ﬁnd for the absolute circulation



· dr =



∇×v

· dS = 0(10.144)

According to Thomson’s theorem (10.131) C

is independent of time so that 6

remains on the side walls. We may now think of the entire surface area of the vortex

10.5 Frictionless barotropic ﬂow 299

(∇ ⫻ v

)

(∇

⫻

)

Fig. 10.8 Flow contours on a vortex tube.

tube’s side wall as being composed of a number of subsections, each bounded by a

certain 6 not enclosing the axis of the vortex. On each one of these boundaries the

circulation vanishes, which means that the vortex tube always consists of the same

particles.

One more important conclusion may be drawn by considering the curve K of the

same ﬁgure enclosing the vortex tube. From (10.143) it follows that the circulation

along K equals the vortex strength of the tube. The circulation along K is constant

in time so that the vortex strength is constant in time also. From this we derive the

important statement that, in case of an ideal barotropic medium, vortices cannot be

created or destroyed. With this statement we close the train of thought beginning

with the Helmholtz vortex theorem from which we derived that ∇×v

remains

zero if it was zero to begin with. A nice and consistent treatment of ﬂow kinematics

is given in Currie (1974).

A barotropic ﬂuid is characterized by a lack of solenoids so that the solenoidal

vector vanishes. Therefore, the Bjerkness circulation theorem (10.119) reduces to

+ 2$

= 0

(10.145)

For the physical interpretation of the remaining terms we refer to Section 10.4.8.

Without any problems equation (10.145) could also have been derived from

Thomson’s theorem (10.111) for a baroclinic ﬂuid.

10.5.4 The vorticity theorem for the barotropic atmosphere

The baroclinic vorticity theorem (10.70) simpliﬁes to its barotropic counterpart on

considering the following points.

(i) The barotropic condition requires ∇α ×∇p = 0.

(ii) There is no twisting or tilting term since the vertical derivatives of the horizontal motion

vanish in the barotropic model atmosphere.

300 Circulation and vorticity theorems

Condition (ii) is satisﬁed if the following prerequisites are valid: (a) barotropy, i.e.

α = α(p), (b) the hydrostatic approximation is valid, and (c) ∂v

/∂p = 0foranyt.

Therefore, equation (10.70) reduces to the barotropic vorticity theorem

dη

=−η ∇

· v

(10.146)

We will discuss this equation in some detail when we deal with the barotropic forecast

model. One more simpliﬁcation is possible by dropping the divergence term in (10.146):

dη

= 0,η= constant

(10.147)

In this case the absolute vorticity is conserved. From this conservation theorem we can

predict changes of the relative vorticity if low- or high-pressure systems are displaced in

the northward or southward direction due to the accompanying changes of the Coriolis

parameter. Consider as an example the southward displacement of a low-pressure system in

the northern hemisphere. Since f is decreasing the relative vorticity is increasing, implying

strengthening of the sys

tem. Equation (10.147) does not, however, give any information

about the trajectory of a displaced system, so the conservation of absolute vorticity is merely

a qualitative tool.

As a ﬁnal point of this section we derive Rossby’s potential vorticity theorem in

the manner suggested by Rossby. In order to do so we need to have recourse to the

continuity equation for a barotropic ﬂuid, which will be derived in a later chapter.

It is given by

(φ − φ

) =−(φ − φ

) ∇

· v

(10.148)

where φ

is the geopotential of the earth’s surface. On eliminating the divergence

term in (10.146) by (10.148) we obtain the conservation equation



φ − φ



= 0,

φ − φ

= P

R,b

(10.149)

where P

R,b

is known as Rossby’s potential vorticity for a barotropic ﬂuid.Weshall

refrain from discussing it at this point.

Our discussion on vortex theorems is far from complete. In an early paper,

Fortak (1956) already addressed the question of the general formalism of vortex

theorems. As a ﬁnal remark in this chapter, we would like to point out that research

on the existence of conservation laws for special conditions has not ceased. Two

examples are papers by Herbert and Pichler (1994) and Egger and Sch

ar (1994),

which deserve serious study.