Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

10.2 The baroclinic Weber transformation 271

Example 2

Since the q

may be expressed as functions of the Cartesian coordinates,

we may consider these as independent ﬁeld functions of x

.Letψ be an arbitrary

ﬁeld function, s the speciﬁc entropy (˙s = 0 for isentropic processes), and P the

potential vorticity, which has not yet been discussed. P turns out to be an invariant

quantity if certain conditions are met. Substitution of these assignments into (10.8)

gives

(α ∇

ψ ·∇

s ×∇

P ) = α



∇



dψ



·∇

s ×∇

P +∇

ψ ·∇





×∇

+∇

ψ ·∇

s ×∇





(10.13)

For isentropic motion (˙s = 0), with, as will be shown later,

P = 0also,weﬁnd

(α ∇ψ ·∇s ×∇P ) = α ∇

dψ

·∇s ×∇P (10.14)

where we have omitted the reference to Cartesian coordinates. This equation has

the form of an interchange relation of operators, which we recognize by setting

d()

,δ

= α ∇s ×∇P ·∇() (10.15)

so that

ψ = δ

ψ (10.16)

10.2 The baroclinic Weber transformation

The Weber transformation is an essential tool in the derivation of circulation the-

orems and hydrodynamic invariants. We begin the somewhat lengthy but straight-

forward derivation by restating equation (3.54), which gives the transformation

between the Lagrangian and the Cartesian coordinates:

∂ψ

∂a

∂x

∂a

∂ψ

∂x

∂ψ

∂x

∂a

∂x

∂ψ

∂a

(10.17)

Next we introduce the speciﬁc entropy s of dry air into the equation of absolute

motion for frictionless ﬂow by eliminating the pressure-gradient term. Using Gibbs’

fundamental equation in the form for the enthalpy h (see TH or any other textbook

on thermodynamics)

h = Td

s + αd

p with h = e + pα (10.18)

272 Circulation and vorticity theorems

and recalling that d

ψ = dr ·∇ψ, we may immediately deduce that

∇h = T ∇s + α ∇p (10.19)

On substituting this equation into the equation of motion

=−∇φ

− α ∇p (10.20)

we obtain

=−∇(φ

+ h) + T ∇s (10.21)

In component form, using Cartesian coordinates, (10.21) reads

=−

∂

∂x

(φ

+ h) + T

∂s

∂x

,k= 1, 2, 3(10.22)

This equation may also be written in Lagrangian coordinates by simply replac-

ing d

/dt

by (∂

/∂t

)

, see Section 3.2.1, where the subscript L denotes the

Lagrangian system. Multiplying (10.22) on both sides by ∂x

/∂a

andthensum-

ming over k,wehave

∂x

∂a



∂

∂t



=−

∂x

∂a

∂

∂x

(φ

+ h) + T

∂s

∂x

∂a

(10.23)

Using (10.17) in (10.23), we obtain

∂x

∂a



∂

∂t



=−

∂

∂a

(φ

+ h) + T

∂s

∂a

(10.24)

We will now integrate this equation assuming isentropic ﬂow ( ˙s = 0). First the

left-hand side of (10.24) will be rewritten as

∂x

∂a



∂

∂t





∂

∂t



∂x

∂a

∂x

∂t



−



∂x

∂t



∂

∂a



∂x

∂t



(10.25)

The second term on the right-hand side is equal to

∂

∂a



∂x

∂t

∂x

∂t



∂

∂a





(10.26)

so that (10.24) assumes the form



∂

∂t



∂x

∂a

∂x

∂t



∂L

∂a

+ T

∂s

∂a

(10.27)

10.2 The baroclinic Weber transformation 273

with

− φ

− h (10.28)

The symbol L

is the Lagrangian function in the absolute system. This function will

be treated in great detail in later chapters. Since we assumed isentropic conditions,

we have



∂s

∂t



= 0(10.29)

so that s is constant on the ﬂuid-particle trajectory. Next we introduce the action

integral of the absolute system:



(10.30)

and similarly

β =



Tdt or

dβ

β = T (10.31)

where T is the absolute temperature. Using this notation, we carry out the time

integration of (10.27) and ﬁnd



∂x

∂a

∂x

∂t



L,t



∂x

∂a

∂x

∂t



t=0

∂W

∂a

+ β

∂s

∂a

(10.32)

since the enumeration coordinates do not change with time. It should be recognized

that the ﬁrst term on the right-hand side is invariant in time. In the Eulerian system

this invariance may be stated as



∂x

∂a

∂x

∂t



t=0

= 0(10.33)

At time t = 0, as before, we require that the Lagrangian and the Eulerian systems

coincide so that



∂x

∂a

∂x

∂t



t=0



∂x

∂t



t=0



∂x

∂t



t=0



∂x

∂t



t=0





t=0

(10.34)

Using this identity, we ﬁnally get from (10.32) the expression



∂x

∂a

∂x

∂t



L,t



∂x

∂t



t=0

∂W

∂a

+ β

∂s

∂a

(10.35)

274 Circulation and vorticity theorems

It is desirable to return to the x

system. This is accomplished by setting i = r in

(10.35), multiplying both sides by (∂a

/∂x

), and then summing over r. The result is



∂a

∂x

∂a

∂x

∂t



L,t

∂a

∂x



∂x

∂t



t=0

∂a

∂x

∂W

∂a

+ β

∂a

∂x

∂s

∂a

(10.36)

We now recall (10.17), where we put i = k and n = r for conformity of notation

with (10.36), yielding

∂ψ

∂x

∂a

∂x

∂ψ

∂a

(10.37)

Now we identify ψ = x

,ands in succession, and ﬁnd

∂x

∂a

∂x

∂a

= δ

∂W

∂x

∂a

∂x

∂W

∂a

∂s

∂x

∂a

∂x

∂s

∂a

(10.38)

Using these expressions in (10.36) we obtain



∂x

∂t



∂a

∂x



∂x

∂t



t=0

∂W

∂x

+ β

∂s

∂x

,k= 1, 2, 3(10.39)

Next we write (10.39) down for k = 1, 2, 3 and multiply each equation by the unit

vectors i, j, k, respectively. By adding the results and using the deﬁnitions

∇a

= i

∂a

∂x

+ j

∂a

∂x

+ k

∂a

∂x

and v

= iu

+ jv

+ kw

with



∂x

∂t



= u



∂x

∂t



= v



∂x

∂t



= w

(10.40)

we obtain the absolute velocity

= u

∇a

+ v

∇a

+ w

∇a

+∇W

+ β ∇s

(10.41)

This equation is the general Weber transformation. The sufﬁx 0 refers to t = 0. We

observe that

˙u

= 0, ˙v

= 0, ˙w

= 0, ˙a

= 0(10.42)

Now we deﬁne the relation

(a) B

= v

−∇W

− β ∇s =⇒

(b) ∇×B

=∇×v

−∇β ×∇s

(10.43)

With (10.43a) the Weber transformation can be written more brieﬂy as

= u

∇a

+ v

∇a

+ w

∇a

(10.44)

As stated at the beginning of this chapter, the Weber transformation serves as an

important tool in some parts of the following sections.

10.3 The baroclinic Ertel–Rossby invariant 275

10.3 The baroclinic Ertel–Rossby invariant

A ﬁrst application of the Weber transformation (10.41) in combination with Ertel’s

version of the continuity equation (10.8) will now be given. Here we replace the

coordinates q

) by the conservative ﬁeld functions ψ

,i = 1, 2, 3. In this case

the continuity equation becomes



αJ

(ψ

,ψ

)





α ∇ψ

·∇ψ

×∇ψ



= 0(10.45)

ThenextstepistotakethecurlofB

, yielding

∇×B

=∇u

×∇a

+∇v

×∇a

+∇w

×∇a

(10.46)

Scalar multiplication of this expression by αB

yields for the right-hand side

αB

·∇×B

= α(v

∇a

·∇u

×∇a

+ w

∇a

·∇u

×∇a

+ u

∇a

·∇v

×∇a

+ w

∇a

·∇v

×∇a

+ u

∇a

·∇w

×∇a

+ v

∇a

·∇w

×∇a

)

(10.47)

In view of (10.42) and (10.45) we ﬁnd that d/dt of each term is zero. Thus, for the

absolute system, we ﬁnd

(αB

·∇×B

) = 0

(10.48)

The invariant ﬁeld function

= αB

·∇×B

(10.49)

is called the baroclinic Ertel–Rossby invariant. For additional details see Ertel and

Rossby (1949). For relative motion on the rotating earth we replace v

by v + v

with v

= $ × r and obtain with (10.43b)

{α(v + v

−∇W

− β ∇s) · [∇×(v + v

) −∇β ×∇s]}=0(10.50)

where the action integral (10.28) is now given by





(v + v

)

− φ − h



dt (10.51)

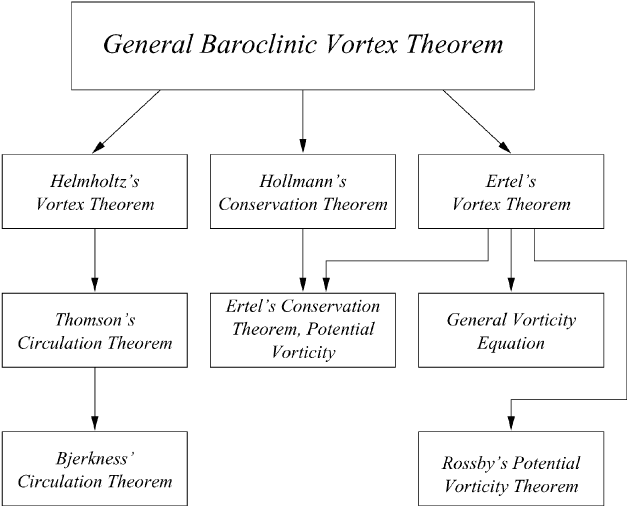
276 Circulation and vorticity theorems

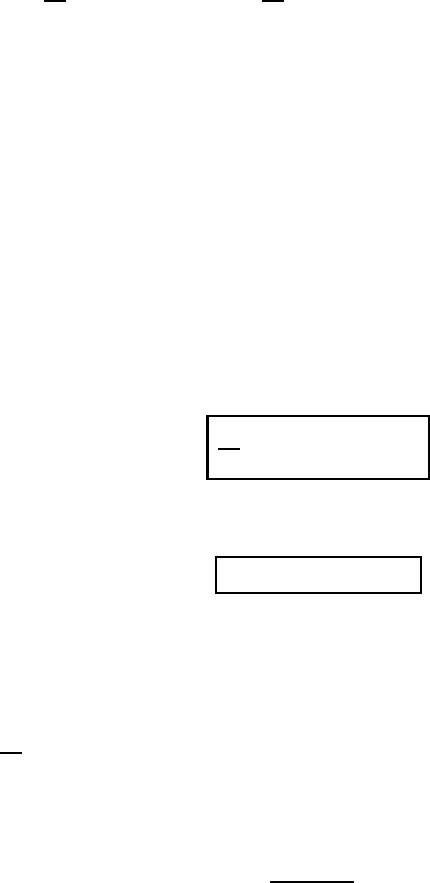
Fig. 10.1 A ﬂow chart for the derivation of vortex and circulation theorems.

10.4 Circulation and vorticity theorems for frictionless baroclinic ﬂow

In the previous section we have given a ﬁrst example of an invariant. Other invariants

will be derived in the next section, together with the equations describing the

circulation and vorticity in baroclinic media. There are various ways of obtaining

the desired results irrespective of the historic development. At the beginning of

our analysis we derive a very general baroclinic vortex law from which all other

considerations follow as shown in Figure 10.1.

10.4.1 A general baroclinic vortex theorem

The ﬁrst step in the derivation of the general baroclinic vortex theorem is taken

by performing scalar multiplication of (10.46) by α ∇ψ,whereψ is an arbitrary

scalar ﬁeld function that is not necessarily invariant. We simply obtain

α ∇×B

·∇ψ = α ∇u

×∇a

·∇ψ +α ∇v

×∇a

·∇ψ +α ∇w

×∇a

·∇ψ

= αJ(u

,ψ) + αJ (v

,ψ) + αJ (w

,ψ)

(10.52)

10.4 Frictionless baroclinic ﬂow 277

Consider, for example, the ﬁrst term on the right-hand side of this equation. Since

and a

are invariants, we ﬁnd from Ertel’s version of the continuity equation

that



αJ(u

,ψ)



= αJ(u

ψ)(10.53)

For convenience we have omitted the sufﬁx x on the Jacobian J . Corresponding

equations can be written for the second and third terms on the right-hand side of

(10.52). Therefore, taking the individual time derivative of (10.52), we ﬁnd

˙s = 0:

(α ∇×B

·∇ψ) = αJ(u

ψ) + αJ (v

ψ) + αJ (w

ψ)

= α ∇×B

·∇

(10.54)

This is the desired general vortex law for the absolute system where the arbitrary

ﬁeld function ψ is at our disposal and may be assigned to various variables. Since

the Weber transformation was obtained for the case of isentropic motion, we must

not ignore the condition ˙s = 0 as expressed in (10.54). If additionally the arbitrary

ﬁeld function ψ is invariant, i.e.

ψ = 0, then (10.54) reduces to Hollmann’s

conservation law

˙s = 0,

ψ = 0:

(α ∇×B

·∇ψ) = 0

(10.55)

The paper by Hollmann (1965) should be consulted for further details. In contrast

to (10.48), now we have a one-parametric conservation law since the arbitrary

ﬁeld function ψ is still at our disposal. The only restriction on ψ is that it must

be invariant. Transformation of (10.54) and (10.55) into the relative system of the

rotating earth gives

˙s = 0:

{α[∇×(v + v

) −∇β ×∇s] ·∇ψ}=α



∇×(v + v

) −∇β ×∇s



·∇

˙s = 0,

ψ = 0:

{α[∇×(v + v

) −∇β ×∇s] ·∇ψ}=0

(10.56)

where we have replaced B

by means of (10.43a).

278 Circulation and vorticity theorems

10.4.2 Ertel’s vortex theorem

The general baroclinic vortex theorem contains Ertel’s vortex theorem (Ertel, 1942)

as a special case. We show this by introducing (10.43b) into (10.54). This results

in the following equation:

(α ∇×v

·∇ψ) −



αJ(β, s, ψ)



= α ∇×v

·∇

ψ − αJ(β, s,

ψ)(10.57)

Since ˙s = 0 by assumption, we ﬁnd from Ertel’s form of the continuity

equation (10.8) for the second term on the left of (10.57) with

β = T (see (10.31))

the expression



αJ(β, s, ψ)



= αJ(T,s,ψ) + αJ(β, s,

ψ)(10.58)

The ﬁrst term on the right-hand side can be reformulated with the help of Gibbs’

fundamental equation for frictionless dry air in the form (10.19). Taking the curl

of this expression, we ﬁnd

∇T ×∇s =−∇α ×∇p (10.59)

Using the deﬁnition of the Jacobian J (T,s,ψ), we ﬁnd from (10.59)

J (T,s,ψ) =∇p ×∇α ·∇ψ (10.60)

so that (10.57) can ﬁnally be written as

(α ∇×v

·∇ψ) − α ∇×v

·∇

ψ = α ∇p ×∇α ·∇ψ = αJ (p, α, ψ)

(10.61)

This is Ertel’s celebrated vortex theorem from which various other theorems follow,

as shown in Figure 10.1. If this theorem is required for the system of the rotating

earth, then the velocity v

must be replaced by v + v

. The interested reader may

wish to read a paper by Ertel (1954). Moreover, Fortak (1956) has addressed the

question of general hydrodynamic vortex laws.

10.4.3 Ertel’s conservation theorem, potential vorticity

First of all we observe that the right-hand side of (10.61) vanishes not only when

the barotropic condition (∇p ×∇α = 0) applies but also if the arbitrary function

ψ depends on α and p so that ψ = ψ(α, p). The speciﬁc entropy possesses this

property, so we may write

∇s =



∂s

∂p



∇p +



∂s

∂α



∇α (10.62)

10.4 Frictionless baroclinic ﬂow 279

For isentropic state changes we ﬁnd from (10.61) the important conservation law

(α ∇×v

·∇s) = 0

(10.63)

The expression

= α ∇×v

·∇s

(10.64)

is known as the potential vorticity or Ertel’s vortex invariant. This conservation law

is valid for isentropic motion. There exists another conservation law leading to the

formulation of the potential vorticity according to Rossby (1940). This formulation

will be discussed in a later section.

It is interesting to remark that Ertel’s conservation theorem could have been

obtained directly from the general vortex theorem (10.54) by setting ψ = s.

10.4.4 The general vorticity theorem

There are various ways to derive the general vorticity theorem. A very elegant

way is based on Ertel’s vortex theorem which we will use to derive the general

vorticity equation in geographical coordinates. Owing to the rigid rotation of the

geographical coordinate system with v

= Ω × r we have

∇·v

= 0, ∇×v

= 2Ω = 2$ sin ϕ e

+ 2$ cos ϕ e

= f e

+ le

(10.65)

Now we deﬁne the relative vorticity ζ and the absolute vorticity, η by means of

ζ = e

·∇×v,η= e

·∇×v

= ζ + f

(10.66)

On setting ψ = r in Ertel’s vortex theorem (10.61) and using the deﬁnition of the

absolute vorticity, we obtain with ˙r = w and ∇r = e

dη

=∇×v

·∇w +∇p ×∇α · e

− η ∇·v

(10.67)

where use of the continuity equation has been made. We now introduce the ge-

ographical coordinates and describe the relative velocity by means of physical

280 Circulation and vorticity theorems

measure numbers (u, v, w). This requires several manipulations, which are listed

∇·v

=∇·v

h,A

+∇·(e

w) =∇

· v

∂w

∂r

∇×v

=∇×v + 2Ω

= (∇×v)

+ (∇×v)

+ le

+ f e

= (∇×v)



(∇×v)

+ l



+ ηe

∇×v

·∇w ={(∇×v)



(∇×v)

+ l



}·∇

w + η

∂w

∂r

=−

r cos ϕ

∂w

∂λ



∂v

∂r



∂w

∂ϕ



∂u

∂r

+ l



+ η

∂w

∂r

∇p ×∇α · e



∇

p + e

∂p

∂r





∇

α + e

∂α

∂r



· e

=∇

p ×∇

α · e

(10.68)

Here we have identiﬁed the horizontal part of the gradient operator by the sufﬁx

h. Substitution of these expressions into (10.67) gives the vorticity equation in

geographical coordinates:

dη

=−η



∇

· v



−

r cos ϕ

∂w

∂λ



∂v

∂r



∂w

∂ϕ



∂u

∂r

+ l



+∇

p ×∇

α · e

(10.69)

A scale analysis of the vorticity equation would show that the underlined terms may

be omitted. If this is done we obtain the simpliﬁed form of the vorticity equation

dη

=−η ∇

· v

+∇

w · e

∂v

∂r

+∇

p ×∇

α · e

(10.70)

where we have made use of

∂v

∂r

=−e

∂v

∂r

+ e

∂u

∂r

(10.71)

According to (10.70) the change of the absolute vorticity with time is due to

three effects.

(i) The divergence effect describing the horizontal divergence of the two-

dimensional ﬂow (the ﬁrst term on the right-hand side).

(ii) Production of vorticity due to the interaction of the vertical gradient of the horizontal

velocity with the horizontal gradient of the vertical velocity. This tipping-term effect