Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

9.6 The zeroth-order discontinuity surface 261
h
h h
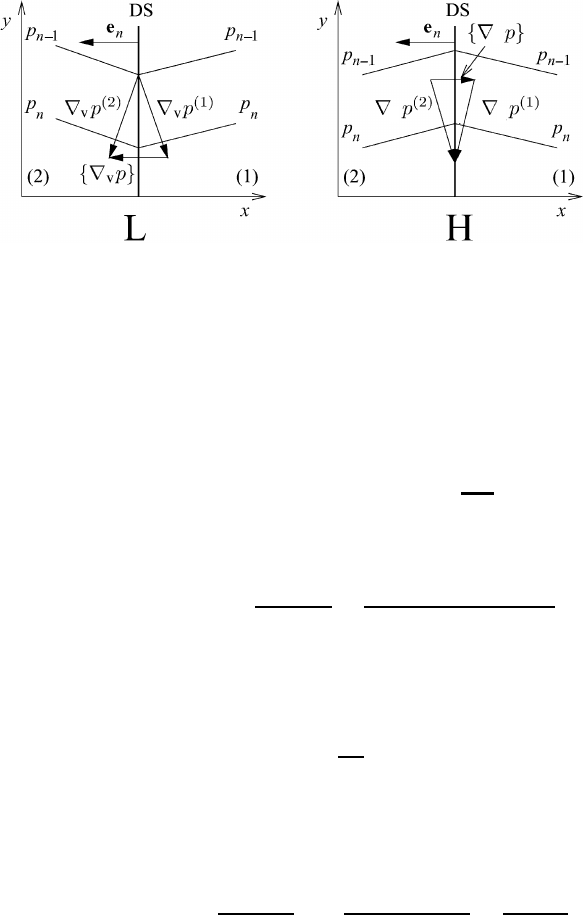
Fig. 9.12 Allowed (left) and forbidden (right) pressure-gradient jumps.
For simplicity we have omitted the vertical bar on the individual time derivative
of v
h
expressing that the basis vectors are not to be differentiated with respect to
time. This equation may be easily obtained by combining the horizontal equation
of motion (2.29) with the hydrostatic approximation (2.27). From (9.55) we obtain
for the jump of the pressure gradient
{
∇p
}
=−gk
{
ρ
}
+ f
{
ρv
}
i − f
{
ρu
}
j −
ρ
dv
h
dt
(9.56)
The inclination of the DS according to (9.51a) or (9.52) can then be expressed by
tan α = i ·∇
v
z
DS
=
i ·
{
∇
v
p
}
g
{
ρ
}
=
−{ρdu/dt}+f
{
ρv
}
g
{
ρ
}
since i ·
{
∇p
}
= i ·
{
∇
v
p
}
(9.57a)
Owing to the special orientation of the coordinate system (∂/∂y = 0) we also
obtain
j ·
{
∇p
}
= j ·
{
∇
v
p
}
=−
ρ
dv
dt
− f
{
ρu
}
= 0(9.57b)
Now we assume that the acceleration is zero so that du/dt and dv/dt vanish.
Since we also ignore viscosity effects, the flow is geostrophic. Therefore, we may
write
(a) tan α = i ·∇
v
z
DS
=
i ·
{
∇
v
p
}
g
{
ρ
}
=−
f i · k ×{ρv
g
}
g
{
ρ
}
=
f {ρv
g
}
g
{
ρ
}
(b) j ·
{
∇
v
p
}
=−f j · k ×{ρv
g
}=−f { ρu
g
}=0 =⇒ i ·{ρv
g
}=0
(9.58)
Equation (9.58b) leads to the conclusion that
ρv
g
lies along the surface of
discontinuity. Moreover, it follows that the geostrophic momentum perpendicular
to the trace of the DS is equal on both sides of the boundary surface. A slope of the
DS of 1:50 is considered steep whereas 1:300 is regarded as shallow.

262 Boundary surfaces and boundary conditions
For purely horizontal geostrophic motion we find from (9.28) and (9.58b)
c
h
= u
(1)
g
= u
(2)
g
= u
g
{ρu
g
}=
{
ρ
}
u
g
=
{
ρ
}
c
h
= 0
{ρ} = 0 =⇒ c
h
= 0butv
(i)
g
= 0
(9.59)
Since the density jump across the DS is assumed to differ from zero, we find that,
for the geostrophic case, the displacement along the x-axis c
x
= c
h
must vanish.
However, in case of accelerated horizontal flow, we find from (9.57b) together with
(9.28) the following relation:
−f
{
ρ
}
c
h
−
ρ
dv
dt
= 0(9.60)
or
c
h
= c
x
=−
{
ρdv/dt
}
f
{
ρ
}
(9.61)
Therefore, for purely horizontal flow a displacement of the front in the x-direction
is possible only if the flow is accelerated in the y-direction.
For the geostrophic flow the wind direction must be parallel to the isobars. Since
the pressure-gradient jump is cyclonic, the horizontal wind shear along the DS must
be cyclonic also. According to the kinematic boundary condition, the velocity jump
is located along the DS. From Figure 9.13 it can be seen that {v
g
} is directed along
the negative y-axis. The direction of {v
g
} can also be found from the condition
tan α>0. This will be shown shortly. For reference see also Figure 9.8.
Fig. 9.13 Cyclonic (allowed) and anticyclonic (forbidden) wind shear in geostrophic flow
at a discontinuity surface.
9.6 The zeroth-order discontinuity surface 263
Let us briefly return to equation (9.58a) and consider three special cases. (i) If
{
ρ
}
= 0thenα = 90
◦
and no boundary surface exists. (ii) If
ρv
g
= 0but
{
ρ
}
= 0, then α = 0 and the boundary surface is horizontal. (iii) If v
(1)
g
= v
(2)
g
= v
g
is assumed then the inclination of the boundary surface DS equals the inclination
of an isobaric surface. From (9.58a) it follows that
tan α = i ·∇
v
z
DS
=
fv
g
g
=
1
ρg
∂p
∂x
= tan α
p
(9.62)
Let us rewrite (9.58a) with the help of the ideal-gas law and express the density
in terms of the virtual temperature. Since the pressure at the boundary surface is
continuous, we obtain immediately
∇
v
z
DS
=−
f k ×
ρv
g
g
{
ρ
}
=
f k ×
T
(1)
v
v
(2)
g
− T
(2)
v
v
(1)
g
g
T
(2)
v
− T
(1)
v
(9.63)
Expressing the geostrophic wind and the virtual temperature in the two different
air masses separated by the DS in terms of their mean values
v
g
=
u
(1)
g
+ u
(2)
g
2
i +
v
(1)
g
+ v
(2)
g
2
j,
T
v
=
T
(1)
v
+ T
(2)
v
2
(9.64)
and jumps, we find
v
(2)
g
= v
g
+
v
g
2
, v
(1)
g
= v
g
−
v
g
2
T
(2)
v
= T
v
+
{
T
v
}
2
,T
(1)
v
= T
v
−
{
T
v
}
2
(9.65)
On substituting (9.65) into (9.63) we obtain
∇
v
z
DS
=
f
g
k ×
v
g
T
v
{
T
v
}
− v
g
(9.66)
As follows from comparison with (9.62), the second term on the right-hand side
represents the inclination of an isobaric surface whose average midlatitude incli-
nation is approximately ±10
−4
. For average atmospheric conditions the first term
in (9.66) is approximately 30 times larger than the second term. If we ignore the
second term we obtain with acceptable accuracy for the inclination of the boundary
surface
tan α = i ·∇
v
z
DS
≈
f
T
v
g
{
T
v
}
i · k ×
v
g
> 0(9.67)

264 Boundary surfaces and boundary conditions
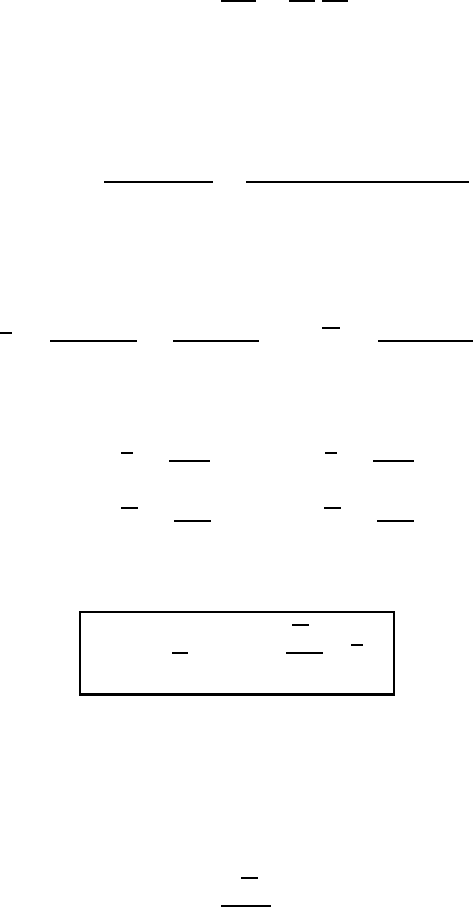
Fig. 9.14 The positions of the warm and the cold air relative to the jump of the geostrophic
wind.
This expression admits an important interpretation. According to the kinematic
boundary-surface condition the jump
v
g
must lie in the DS and can be interpreted
as a horizontal as well as a vertical jump. Since the warm air overlies the wedge
of cold air, the temperature jump
{
T
v
}
must be positive. A consequence of the
condition tan α>0isthat
v
g
must have the direction shown in Figure 9.14.
Thus, looking in the direction of
v
g
, the warm air must always be situated to
the right of the jump
v
g
, as shown in the figure. This result is in agreement with
Figure 9.13.
The behavior of
v
g
with respect to the positions of the warm and the cold air
corresponds exactly to the behavior of the thermal wind v
T
in the continuous field.
The thermal wind is defined as the variation of the geostrophic wind with height. For
convenience, we will consider geostrophic motion on an isobaric surface. Thus we
have to transform the equation for the geostrophic wind from the (x, y,z)-system
to the (x, y,p)-system. This is easily accomplished with the help of (M4.51) by
setting there q
3
= z, ξ = p,andψ = p. Utilizing the hydrostatic equation together
with φ = gz, we obtain ∇
h,z
p = ρ ∇
h,p
φ so that the equation for the geostrophic
windinthep system is given by
v
g
=
1
f
k ×∇
h,p
φ (9.68)
On differentiating this equation with respect to pressure we obtain the differential
form of the thermal wind in the p system:
∂v
g
∂p
=
1
f
k ×∇
h,p
∂φ
∂p
=−
1
f
k ×∇
h,p
1
ρ
=−
R
0
fp
k ×∇
h,p
T
v
(9.69)
A slight rearrangement of this formula gives
v
T
= v
g
=
∂v
g
∂φ
φ =
∂v
g
∂p
∂p
∂φ
φ =
φ
fT
v
k ×∇
h,p
T
v
(9.70)

9.7 An example of a first-order discontinuity surface 265
Fig. 9.15 The positions of the warm and cold air relative to the thermal wind, subscripts
l and u refer to lower and upper layers.
showing that the warm air is always located to the right of the thermal wind; see
Figure 9.15.
It can be recognized from Figure 9.15 that clockwise turning of the geostrophic
wind with height (veering) is associated with warm-air advection whereas anti-
clockwise turning (backing) with height causes cold-air advection. The rule is
reversed in the southern hemisphere.
At the conclusion of this section we wish to point out that mathematical expres-
sions for obtaining general equations for the slope of discontinuity surfaces for
accelerated frictionless flow have been worked out. These expressions are not very
important for our work and will be omitted.
9.7 An example of a first-order discontinuity surface
An important example of a first-order discontinuity surface is the tropopause,
where the temperature is continuous while the vertical temperature gradient is
discontinuous; see Figure 9.16. We will only briefly consider this subject and
calculate the midlatitude slope of the tropopause. More detailed information is
given, for example, by Lowell (1951); see also Haltiner and Martin (1957).
Let us consider two points along the tropopause. The temperature variation along
the tropopause is approximately given by
d
g
T
(i)
=
∂T
∂x
(i)
dx +
∂T
∂z
(i)
dz, i = 1, 2(9.71)
with d
g
T
(1)
= d
g
T
(2)
. Since the geometric variation is the same on both sides of
the DS, we find upon subtraction
∂T
∂x
dx +
∂T
∂z
dz = 0(9.72)
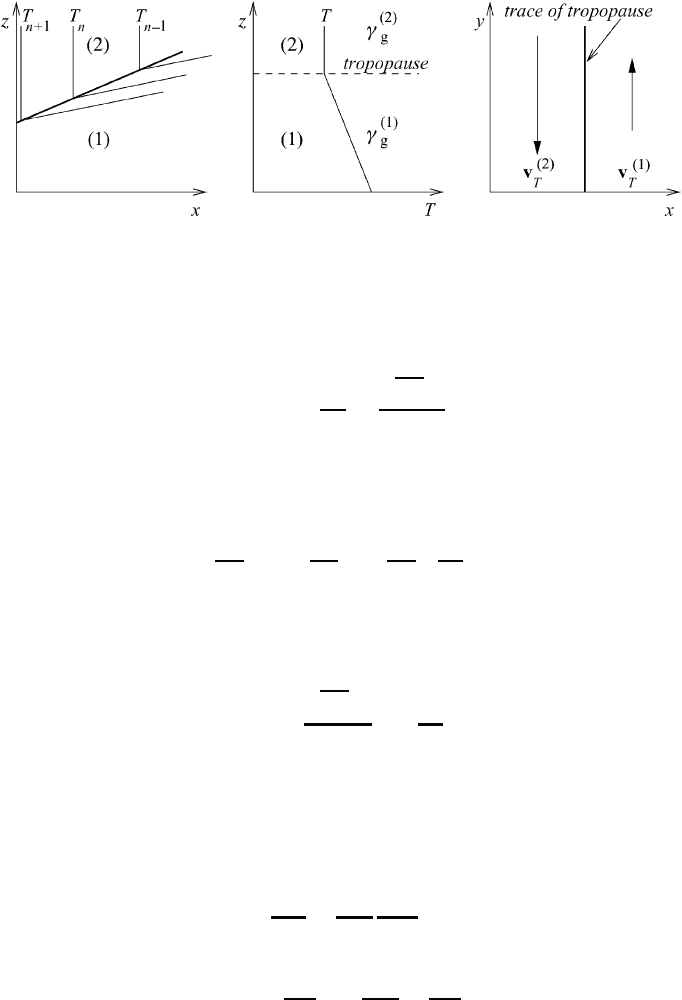
266 Boundary surfaces and boundary conditions
Fig. 9.16 The temperature distribution and the geostrophic wind shear at the tropopause.
The x-axis is pointing toward the equator.
The slope of the tropopause is then given by
tan α
T
=
dz
dx
=
∂T
∂x
z
γ
g
(9.73)
where
γ
g
represents the jump of the lapse rate. We now transform from the
z-system to the pressure system by using the transformation rule
∂T
∂x
z
=
∂T
∂x
p
−
∂T
∂z
∂z
∂x
p
(9.74)
This expression is obtained from (M4.51) by setting there q
1
= x, q
3
= z,and
ζ = p. Thus we find
tan α
T
=
∂T
∂x
p
γ
g
+
∂z
∂x
p
(9.75)
where the second term represents the slope of the pressure surface in the x-direction.
Using the definition of the geostrophic wind in the pressure system (9.68) and
rewriting the thermal-wind equation (9.69) with the help of the hydrostatic equation,
we find with T ≈ T
v
tan α
T
=
fv
g
g
+
T
v
f
g
{
v
T
}
γ
g
with
{
v
T
}
=
∂v
g
∂z
=
g
fT
v
∂T
v
∂x
p
(9.76)
Here v
T
is the differential form of the thermal wind. From the temperature distri-
bution in the vicinity of the tropopause we find the direction of the geostrophic
9.8 Problems 267
wind shear along the trace of the tropopause. Assuming that v
(1)
T
= 4ms
−1
km
−1
,
v
(2)
T
=−6ms
−1
km
−1
, v
g
= 30 m s
−1
, T = 240 K at the tropopause, and
γ
g
= 6Kkm
−1
, we find from (9.76) tan α
T
= 43 m (10 km)
−1
. This means that,
in the midlatitudes, the tropopause rises by about 43 m if we move a distance of
10 km toward the equator.
It should be observed that there exists no entirely satisfactory theory for the
formation and the existence of the tropoause, which is not a continuous band rising
from about 9 km at the North pole to 18 km at the equator. The tropopause is often
fractured in the region of strong jet streams, permitting the exchange of air between
the troposphere and the stratosphere.
9.8 Problems
9.1: Let ξ = p. With the help of the proper transformation equations and the
kinematic boundary-surface condition, find an expression for the generalized ver-
tical velocity ω
s
= ˙p
s
for the earth’s surface. This expression should involve the
geopotential.
9.2: With the help of (9.63), find an expression for the slope of the discontinuity
surface.
9.3: Sketch three figures of the type shown in Figure 9.13. Show the distribution
of the isobars, the direction and roughly the magnitude of the geostrophic wind,
and the jump of v
g
for the following three situations:
(a) cold high, warm high,
(b) cold high, warm low,
(c) warm low, warm high.
Place the pressure systems on the appropriate side of the discontinuity surface.
Check your figures by applying the conditions that tan α>0and
v
g
is cyclonic.
10
Circulation and vorticity theorems
In this chapter a number of very important circulation and vorticity theorems
will be introduced. Instead of following the historical development, they will be
deduced from a general baroclinic vortex law in order to demonstrate the close
relationships among the various theorems. This particular way of presentation is
chosen in order to better appreciate the great beauty of the underlying theory.
Of course, the vorticity equation in Cartesian coordinates, for example, could be
easily derived from the horizontal equations of motion by differentiating these with
respect to the horizontal coordinates and subtracting the resulting formulas from
each other. This operational process is easily understood and carried out, but the
reader probably fails to appreciate the fairly general character of the entire theory.
A basic tool needed in the following derivations is Ertel’s form of the continuity
equation, which will be presented in the next section. Another important tool in
our work is the Weber transformation, which will be discussed in Section 10.2.
10.1 Ertel’s form of the continuity equation
The derivation rests on the general formulation of the continuity equation. Using
(M3.56) and (M4.36), equation (1.50) can be written in the following form:
d
dt
ρ
√
g
q
+ ρ
√
g
q
∂ ˙q
n
∂q
n
= 0
with
√
g
q
=
√
g
x
∂(x
1
,x
2
,x
3
)
∂(q
1
,q
2
,q
3
)
=
1
J
x
(q
1
,q
2
,q
3
)
(10.1)
This equation involves a transformation from the Cartesian to the general coor-
dinates as discussed in Section M4.1.3. Replacing the density ρ by the specific
268
10.1 Ertel’s form of the continuity equation 269
volume α and carrying out the differentiation gives
d
dt
αJ
x
(q
1
,q
2
,q
3
)
= αJ
x
(q
1
,q
2
,q
3
)
∂ ˙q
n
∂q
n
(10.2)
In
√
g
q
the partial derivatives with respect to q
k
will now be replaced by using the
proper transformation rules (M4.24):
∂
∂x
i
=
∂q
n
∂x
i
∂
∂q
n
or
∂
∂x
1
∂
∂x
2
∂
∂x
3
=
∂q
j
∂x
i
∂
∂q
1
∂
∂q
2
∂
∂q
3
(10.3)
By inversion of (10.3) we find the expression
∂
∂q
1
∂
∂q
2
∂
∂q
3
=
∂x
j
∂q
i
∂
∂x
1
∂
∂x
2
∂
∂x
3
=
M
·j
i·
J
x
(q
1
,q
2
,q
3
)
∂
∂x
1
∂
∂x
2
∂
∂x
3
(10.4)
where J
x
(q
1
,q
2
,q
3
) = Det(∂q
j
/∂x
i
)andM
·j
i·
are the adjoints of the matrix
(∂q
j
/∂x
i
). It should be kept in mind that the value of a determinant is not changed
by transposition of rows and columns. The reader may easily convince himself that
M
·1
1·
M
·2
1·
M
·3
1·
M
·1
2·
M
·2
2·
M
·3
2·
M
·1
3·
M
·2
3·
M
·3
3·
∂
∂x
1
∂
∂x
2
∂
∂x
3
=
J
x
,q
2
,q
3
J
x
q
1
,,q
3
J
x
q
1
,q
2
,
(10.5)
where, for example,
J
x
( ,q
2
,q
3
) =
∂
∂x
1
∂
∂x
2
∂
∂x
3
∂q
2
∂x
1
∂q
2
∂x
2
∂q
2
∂x
3
∂q
3
∂x
1
∂q
3
∂x
2
∂q
3
∂x
3
(10.6)
270 Circulation and vorticity theorems
By application of (10.4) and using (10.5), we find directly
∂ ˙q
1
∂q
1
∂ ˙q
2
∂q
2
∂ ˙q
3
∂q
3
=
1
J
x
(q
1
,q
2
,q
3
)
J
x
( ˙q
1
,q
2
,q
3
)
J
x
(q
1
, ˙q
2
,q
3
)
J
x
(q
1
,q
2
, ˙q
3
)
(10.7)
Substitution of this expression into (10.2) gives
d
dt
αJ
x
(q
1
,q
2
,q
3
)
= α
J
x
( ˙q
1
,q
2
,q
3
) + J
x
(q
1
, ˙q
2
,q
3
) + J
x
(q
1
,q
2
, ˙q
3
)
(10.8)
where all spatial derivatives are taken with respect to the Cartesian coordinates. This
version of the continuity equation is due to Ertel (1960), and is of great advantage
whenever conservative quantities, i.e. invariant field functions, are involved. These
are always characterized by the conservation equation
dψ
i
dt
=
˙
ψ
i
= 0(10.9)
Two brief examples will demonstrate this.
Example 1 Suppose that the q
k
are the Lagrangian enumeration coordinates a
k
which are characterized by ˙a
k
= 0. Then it is easily seen that the right-hand side
of (10.8) vanishes so that
d
dt
αJ
x
(a
1
,a
2
,a
3
)
=
d
dt
α ∇
x
a
1
·∇
x
a
2
×∇
x
a
3
= 0(10.10)
Thus [α ∇
x
a
1
·∇
x
a
2
×∇
x
a
3
] is an invariant. From (10.1) follows immediately the
continuity equation in Lagrangian enumeration coordinates which was discussed
previously:
d
dt
α
√
g
a
=
∂
∂t
α
√
g
a
a
i
= 0or
d
dt
ρ
√
g
a
=
∂
∂t
ρ
√
g
a
a
i
= 0(10.11)
with (d/dt)(···) = (∂/∂t)(···)
a
i since ˙a
k
= 0. Integration yields
ρ
√
g
a
= constant =
ρ
√
g
a
t=t
0
(10.12)
