Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

8.6 Differential invariants 241

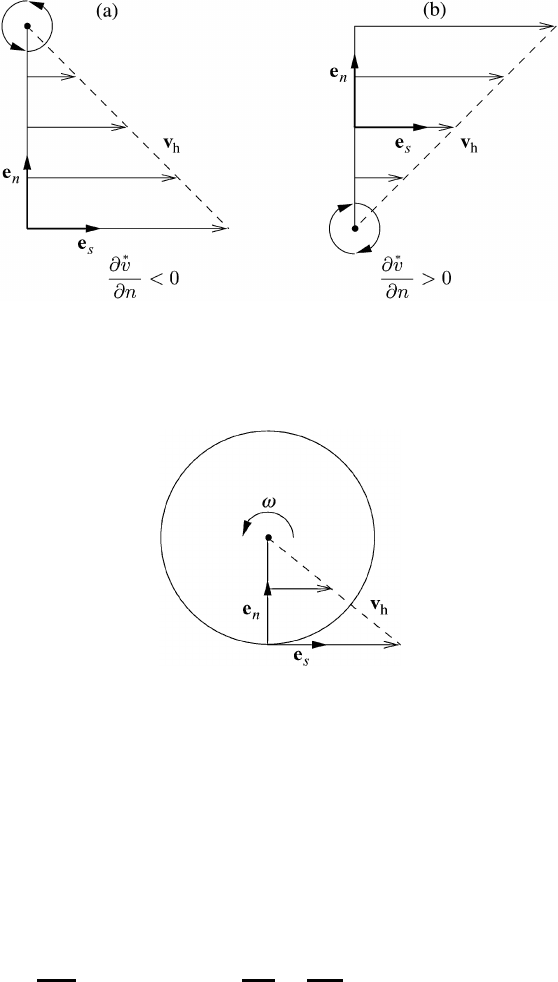
Fig. 8.8 The sign convention for the shear vorticity in northern-hemispheric ﬂow:

(a) cyclonic wind shear, and (b) anticyclonic wind shear.

Fig. 8.9 The vorticity of rigid rotation of a disk.

whereas for anticyclonic ﬂow R

< 0; see Figure 8.2. The physical meaning and

the sign convention for the shear vorticity are shown in Figure 8.8.

Finally, we give a very brief example relating to the vorticity of rigid rotation of

a circular disk with v

= ωR

; see Figure 8.9. The simple calculation is outlined

in equation (8.35), which does not require any additional comment:

ωR

= ω, ζ

=−

∂v

∂n

∂v

∂R

= ω =⇒ ζ = 2ω (8.35)

In large-scale atmospheric motion the order of magnitude of the vorticity

≈10

−4

–10

−5

−1

242 Natural coordinates

8.6.3 The Jacobian operator and the Laplacian

Since we are not going to use these operators, we will not derive them; but we

will state them for reference. They can be derived from the general formulas which

were given previously. Checking the validity of the formulas

J (u, v) =

∂u

∂x

∂v

∂y

−

∂u

∂y

∂v

∂x

= D

+ ζ

∇

ψ =

∂

∂s

∂

∂n

∂ψ

∂s

−

∂ψ

∂n

(8.36)

will be left for the exercises.

8.7 The equation of motion for frictionless horizontal ﬂow

After having taken some interesting but necessary detours, we are now ready to

ﬁnd the equation of motion for frictionless horizontal ﬂow in the natural coordinate

system. We proceed by transforming each term of the equation of motion (2.38) in

the Cartesian system

=−

∇p −∇φ − f e

× v

= e

+ e

(8.37)

The last equation follows from (8.26). The individual derivative of the ﬁrst term on

the right-hand side can be expanded with the help of (8.11) to give



∂v

∂t



n,s,z

+ v

∂v

∂s



∂v

∂t



n,s,z

∂

∂s





n,z,t

(8.38)

The local derivative is explicitly given by (8.28).

The gradient of an arbitrary ﬁeld function ψ is speciﬁed by (8.10) and can be

directly applied to the pressure term and to the geopotential. Assuming that the

geopotential is approximated by φ = gz,weﬁnd

∇φ = ge

(8.39)

The Coriolis term can be written as

−f e

× v

=−f e

× v

=−e

(8.40)

8.8 The gradient wind relation 243

Using these transformations, we ﬁnd the desired equation of motion in the natural

coordinate system:

+ e

=−

∇p − ge

− e

(8.41)

The s-component of this equation yields a prognostic equation for the magnitude

of the velocity:



∂v

∂t



n,s,z

∂

∂s





n,z,t

=−



∂p

∂s



n,z,t

(8.42)

The n-component of (8.41) results in a diagnostic relation involving the balance of

the centripetal force, the pressure gradient force, and the Coriolis force:

=−

∂p

∂n

− fv

(8.43)

while the vertical component of (8.41) is the hydrostatic equation

0 =−

∂p

∂z

− g (8.44)

8.8 The gradient wind relation

If the ﬂow is solely governed by (8.43), we obtain the gradient wind relations. With

the abbreviation v

= v

> 0 equation (8.43) changes into

+ fv

∂p

∂n

= 0(8.45)

Note that ∂p/∂n < 0. First of all, we observe that, if R

−→ ∞, then we obtain

the geostrophic ﬂow, which has already been discussed in an earlier chapter:

=−

ρf

∂p

∂n

> 0,R

−→ ∞ (8.46)

Solving the quadratic equation (8.43) results in the gradient wind equations for

curved cyclonic or anticyclonic ﬂow:

cyclonic ﬂow: v

=−



−

∂p

∂n

> 0

anticyclonic ﬂow: v

=−

−



−

∂p

∂n

< 0

(8.47)

244 Natural coordinates

Note that v

is always positive in the natural coordinate system. The type of ﬂow is

determined by the sign convention which we introduced previously. To prevent the

wind speed from assuming complex values, we must assure that the argument of

the root does not become negative for R

< 0. Therefore, the wind speed around

the high-pressure system is limited to the maximum value

(max) =−

< 0(8.48)

If the pressure gradient force approximately balances the centripetal force then we

obtain the so-called cyclostrophic wind given by

cycl



−

∂p

∂n

> 0(8.49)

This type of ﬂow is important near the centers of tropical cyclones at low latitudes,

where the centripetal force may outweigh the Coriolis force by as much as 25 to

1 as remarked by Byers (1959), so that the term fv

in (8.45) may be neglected.

Similar discussions on gradient ﬂow may be found in various textbooks, e.g. Hess

(1959).

8.9 Problems

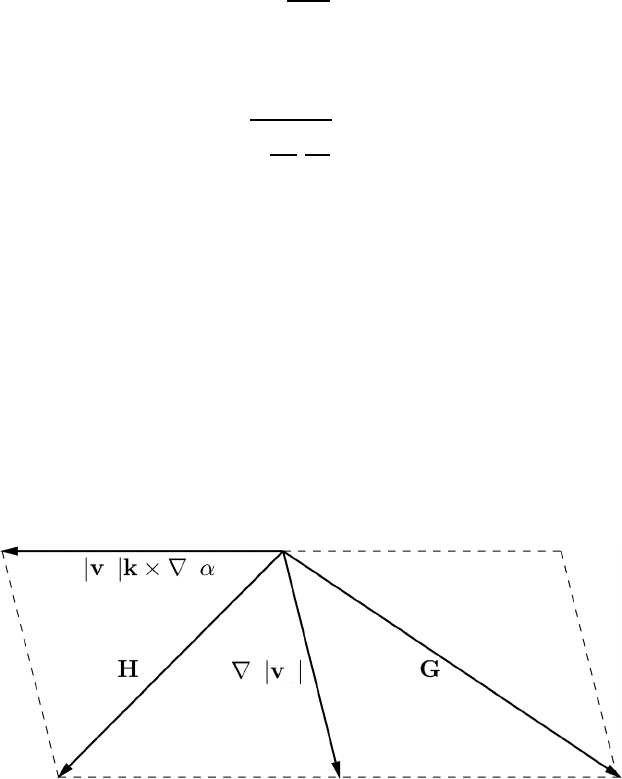
8.1: Let α represent the angle between the x-axis and the horizontal wind vector

. Curves along which α = constant and

= constant are called isogons and

isotachs, respectively. Consider the auxiliary vectors G and H shown in the ﬁgure.

Use natural coordinates to show that

(a) the divergence is given by D = G · e

(b) the vorticity is given by ζ =−G · e

+ ζ

= G

8.9 Problems 245

(d) Let A = ∂u/∂x − ∂v/∂y and B = ∂u/∂y + ∂v/∂x. Show that

A = H · [(cos(2α) e

− sin(2α) e

)]

B = H · [(sin(2α) e

+ cos(2α) e

)]

= H · H = A

+ B

= def

(e) Show that

G = De

− ζ e

H = [A cos(2α) + B sin(2α)]e

+ [−A sin(2α) + B cos(2α)]e

(f) Use the answer to part (e) to demonstrate that the horizontal wind vector v

can

be expressed in terms of the kinematic ﬁelds.

Hint: Consider the arbitrary vector A = A

+ A

. Show that e

= (A

A ×

k + A

A)/(A

+ A

). Replace A by G to show that

+ ζ

[D(∇

−

k ×∇

α) + ζ (k ×∇

∇

α)]

8.2: Suppose that v

·∇

= 0. Show that this statement is equivalent to

D∇

=−

ζ ∇

Hint: Find two expressions for v

·∇

. Obtain one of them with the help of

Lamb’s development, which is also valid for the two-dimensional case.

8.3: Verify equation (8.36).

Boundary surfaces and boundary conditions

9.1 Introduction

The continuity equation and the equation of motion are applicable only to ﬂuid

regions in which the physical variables change in a continuous fashion. Only in

these regions is it possible to form the required derivatives of the variables as they

appear in the various terms of the prognostic and diagnostic equations. However,

there exist external boundary surfaces at which the ﬂuid is constrained by a wall or

bounded by a vacuum, where the ﬁeld functions or their nth derivative experience

discontinuous changes. Such surfaces are called discontinuity surfaces (DSs). At

external as well as internal boundary surfaces the continuity equation and the

equation of motion must be replaced by the so-called kinematic and dynamic

boundary-surface conditions.

It is customary to classify the DS according to its order. A boundary surface is

said to be of nth order if the lowest discontinuous derivative of the ﬁeld function

being considered is of nth order. Let the symbol

{

}

represent the jump experienced

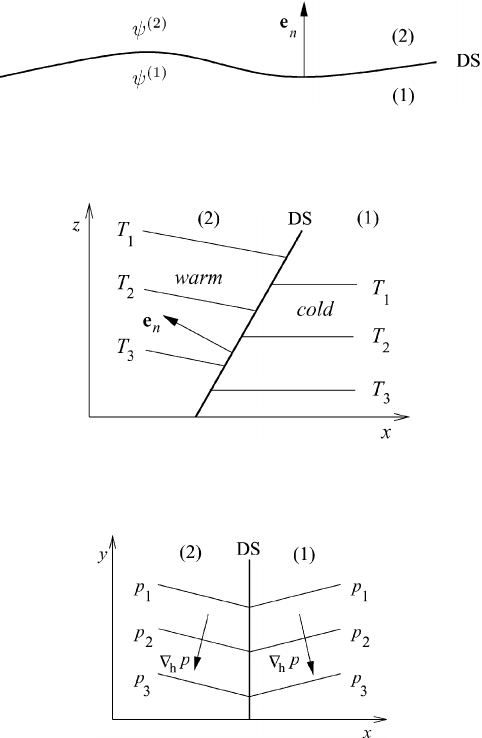
by the ﬁeld function ψ at the DS as shown in Figure 9.1, so that

(2)

− ψ

(1)

{

}

(9.1)

A boundary surface of nth-order discontinuity is then deﬁned by

{

}

= 0,



∂ψ

∂s



= 0,



∂

∂s



= 0, ···,



∂

∂s



= 0(9.2)

Actual discontinuities do not form in the atmosphere but there are narrow zones

of transition between two air masses, which, in large-scale motion, may be viewed

as discontinuities. Consider, for example, an idealized warm front or a cold front

that is a DS of order zero in terms of temperature, density, and wind, that is

{

}

= 0,

{

}

= 0,

{

}

= 0; see Figure 9.2.

246

9.2 Differential operations at discontinuity surfaces 247

Fig. 9.1 A jump of the ﬁeld function at a discontinuity surface.

Fig. 9.2 A discontinuity surface DS of order zero.

Fig. 9.3 A ﬁrst-order DS relative to pressure.

A discontinuity surface of order one is deﬁned by the condition that the ﬁrst

spatial derivative experiences a jump. The tropopause, for example, is a ﬁrst-order

DS relative to temperature, that is

{

}

= 0and

{

∂T/∂z

}

= 0. Frontal surfaces are

DSs of ﬁrst order relative to pressure with

{

}

= 0and

{

∇

}

= 0; see Figure 9.3.

Before we proceed with our discussion, it is imperative to deﬁne various differential

operators applicable to the DS.

9.2 Differential operations at discontinuity surfaces

We consider an arbitrary extensive ﬁeld function ψ, which is assumed to be dis-

continuous at the DS so that we are dealing with a zeroth-order DS. Utilizing the

248 Boundary surfaces and boundary conditions

Fig. 9.4 The deﬁnition of the surface gradient.

general integral theorem (M6.30), in a region where ψ changes in a continuous

fashion, the gradient of ψ may be written as

∇ψ = lim

τ →0

τ



ψdS (9.3)

where τ is an inﬁnitesimally small volume with surface S. In order to account for

the discontinuity of the ﬁeld function at the DS, we introduce the surface gradient

in analogy to (9.3) by means of

 ψ = lim

S→0

S



ψdS (9.4)

where the surface integral is taken over the upper and lower surfaces of the small

cylindrical volume of inﬁnitesimal thickness h; see Figure 9.4.

The contributions by the sides h → 0 of the pillbox to the surface integral are

considered negligible. Integration of (9.4) results in

 ψ = e

(ψ

(2)

− ψ

(1)

) = e

{

}

(9.5)

It should be noted that the superscripts (1) and (2) simply mean that the function ψ

is taken directly at the corresponding sides of the DS. The operator  ψ at the DS

replaces Hamilton’s nabla operator, which is valid only in the continuous region of

the ﬂuid. Therefore, (9.5) is often called the surface Hamilton operator.

For the arbitrary vector Ψ we formally deﬁne the surface divergence for the

zeroth-order DS by

·Ψ = e

{

}

(9.6)

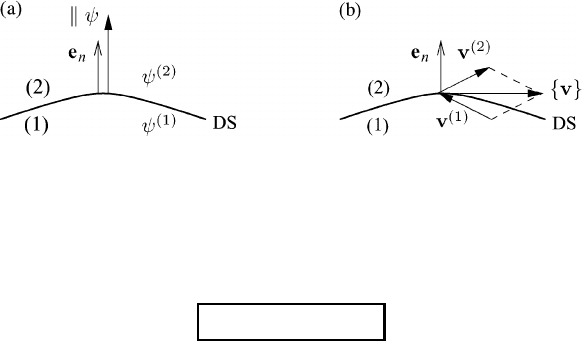
9.2 Differential operations at discontinuity surfaces 249

Fig. 9.5 Surface Hamilton operators for (a) the scalar ﬁeld function ψ and (b) the vectorial

ﬁeld function v.

The surface rotation may be written as

×Ψ = e

{

}

(9.7)

Some brief examples will clarify the concept. Figure 9.5(a) shows the gradient

of the scalar ﬁeld function ψ.Ifψ represents the velocity vector v then the surface

gradient, the divergence, and the rotation are deﬁned by

 v = e

{

}

, ·v = e

{

}

, ×v = e

{

}

(9.8)

We will now consider the following situations.

(i) v is source-free on the DS

Then we have

·v = e

{

}

= 0(9.9)

Since by assumption

{

}

= 0, we must conclude that e

is perpendicular to

{

}

meaning that the velocity jump is located in the plane tangential to the DS; see

Figure 9.5(b). We may also write

· v

(1)

= e

· v

(2)

(9.10)

showing that the normal components of the velocity vector v are continuous on the

DS.

(ii) v is irrotational on the DS

Then we have

×v = e

{

}

= 0(9.11)

From this it follows that

{

}

is parallel or antiparallel to e

, that is perpendicular to

the DS. By writing (9.11) in the form

× v

(1)

= e

× v

(2)

(9.12)

250 Boundary surfaces and boundary conditions

Fig. 9.6 Relevant quantities for the proof of (9.14).

we ﬁnd that the tangential components of the velocity vector are continuous on the

DS.

(iii) ·v = 0and ×v = 0.

The conditions ·v = 0and×v = 0 cannot be satisﬁed simultaneously

on a zeroth-order DS since this would require

{

}

= 0, which contradicts our

assumption.

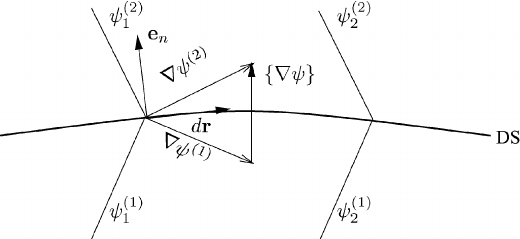
This section will be concluded by proving that, on a ﬁrst-order DS, as deﬁned

{

}

= 0,

{

∇ψ

}

= 0(9.13)

the surface rotation of the gradient must vanish:

×∇ψ = e

{

∇ψ

}

= 0(9.14)

For the proof consider Figure 9.6, where the relevant quantities are shown. The

geometric change d

ψ on both sides of the DS can be represented with the help of

the displacement vector dr which is located along the DS. The gradients of the

ﬁeld function on both sides of the DS are also shown in Figure 9.6, as is the jump

of the gradient

{

∇ψ

}

. The geometric changes are given by

(i)

= dr ·∇ψ

(i)

,i= 1, 2(9.15)

Since the ﬁeld function ψ is continuous on the DS, the geometric changes are the

same on both sides, so we obtain





= dr ·

{

∇ψ

}

= 0ore

{

∇ψ

}

= 0,

{

∇ψ

}

= 0(9.16)

Therefore, the jump

{

∇ψ

}

is orthogonal to the DS as shown in Figure 9.6. This

completes the proof.