Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

7.1 Atmospheric flow fields 221
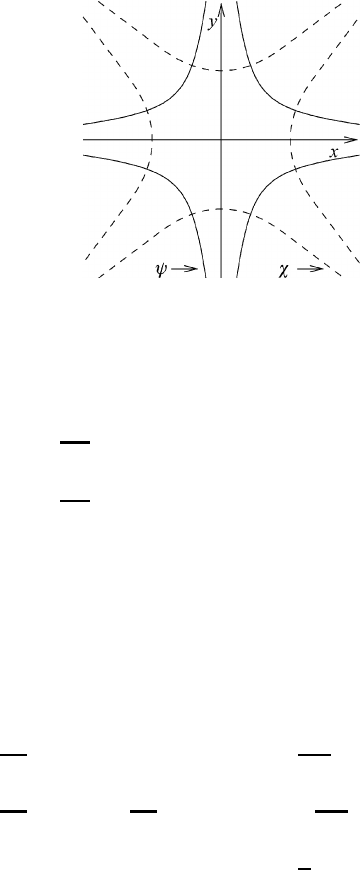
Fig. 7.2 Representative lines of the stream function ψ and lines of constant velocity
potential χ .
Application of the Cauchy–Riemann equations and integration immediately results
in
∂ψ
∂y
=−λx =⇒ ψ =−λxy + f (x)
∂ψ
∂x
=−λy =⇒ ψ =−λyx + f (y)
ψ =−λxy + C
1
(7.13)
Since we are dealing with partial differential equations, integration yields the
functions f (x)andf (y) instead of integration constants. However, comparison of
the first two equations of (7.13) shows that f (x) = f (y) so that both functions
must be equal to a constant. Analogously to ψ, the velocity potential χ is obtained
by using the remaining pair of Cauchy–Riemann equations:
∂χ
∂x
= λx =⇒ χ =
λx
2
2
+ f (y)
∂χ
∂y
=−λy =
df
dy
=⇒ f (y) =−
λy
2
2
+ C
2
χ =
λ
2
(x
2
− y
2
) + C
2
(7.14)
We will now show that, in this situation, the isolines of the stream function and
the velocity potential are orthogonal since the scalar product of the gradients of
∇
h
ψ and ∇
h
χ is zero,
∇
h
ψ ·∇
h
χ =∇
h
ψ · k ×∇
h
ψ = 0(7.15)
A sketch of the flow field is given in Figure 7.2.

222 Kinematics of two-dimensional flow
ψ
∗
= constant
υ
Fig. 7.3 The horiz
ontal streamline
ψ
∗
= constant
.
From the definitions stated in (4.9) one obtains
ζ = 0,D= 0,def=
A
2
+ B
2
= 2λ (7.16)
This verifies the statement that we are dealing with a purely deformational flow
field.
7.2 Two-dimensional streamlines and normals
7.2.1 Two-dimensional streamlines
For the horizontal flow the equation of streamlines (3.39) reduces to
v
h
× dr
s
= 0 =⇒
dy
dx
=
v(x,y, t
0
)
u(x,y, t
0
)
or − udy + vdx = 0(7.17)
where dr
s
is a line element along the streamline. From analysis we know that (7.17)
is an exact differential equation if there exists a function ψ
∗
(x,y) such that
dψ
∗
=
∂ψ
∗
∂y
dy +
∂ψ
∗
∂x
dx =−udy + vdx = 0 =⇒ ψ
∗
(x,y) = constant
(7.18)
See Figure 7.3. The condition of exactness, also known as the integrability
condition,isgivenby
∂
2
ψ
∗
∂x ∂y
=
∂
2
ψ
∗
∂y ∂x
=⇒
∂u
∂x
+
∂v
∂y
=∇
h
· v
h
= 0(7.19)
showing that the divergence of the flow field is zero.
From (7.18) we have
u =−
∂ψ
∗
∂y
,v=
∂ψ
∗
∂x
or v
h
= k ×∇
h
ψ
∗
(7.20)
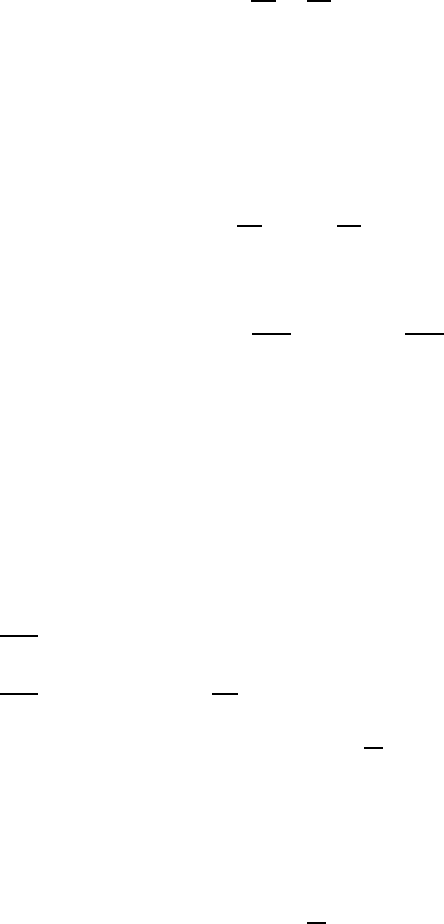
7.2 Two-dimensional streamlines and normals 223
Since the divergence D = 0, the streamline is identical to the stream function, see
(6.11), which is defined by
v
h,ROT
= k ×∇
h
ψ (7.21)
If the divergence differs from zero, the integrability condition (7.19) is not satisfied,
that is
∂u
∂x
+
∂v
∂y
= 0(7.22)
Now the streamlines and lines of the constant stream functions are no longer
identical. In order to find ψ
∗
, we multiply (7.17) by a suitable integrating factor
µ(x,y), causing this equation to become exact,
−uµ dy + vµ dx = 0(7.23)
In this case the integrability condition is given by
−
∂
∂x
(uµ) =
∂
∂y
(vµ)(7.24)
It may be very difficult to find such an integrating factor. If it has been found, we
have to solve
uµ =−
∂ψ
∗
∂y
,vµ=
∂ψ
∗
∂x
(7.25)
to find the streamline ψ
∗
, which is no longer identical to the stream function ψ.
We will now consider a very simple example satisfying condition (7.19) so that
D = 0. If the velocity components are given by
u = U = constant > 0,v=−kA sin(kx)(7.26)
then the equation of the streamline reads
−Udy− kA sin(kx) dx = 0(7.27)
Application of (7.18) results in
(a)
∂ψ
∗
∂y
=−U =⇒ ψ
∗
=−Uy + f (x)
(b)
∂ψ
∗
∂x
=−kA sin(kx) =
df
dx
=⇒ f (x) = A cos(kx) + constant
(c) ψ
∗
= A cos(kx) − Uy + ψ
∗
0
=⇒ y =
1
U
ψ
∗
0
− ψ
∗
+ A cos(kx)
(7.28)
where the integration constant has been denoted by ψ
∗
0
. The solution is a flow field
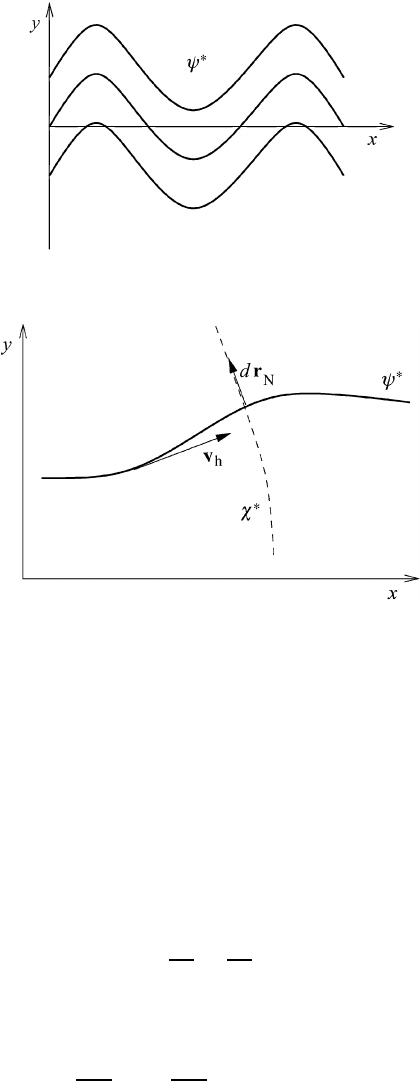
representing a stationary Rossby wave; see Figure 7.4.
If the wave is displaced with the phase velocity c in the eastward direction then
the last equation of (7.28) must be modified to read
y = constant +
A
U
cos[k(x − ct)] (7.29)
224 Kinematics of two-dimensional flow
Fig. 7.4 Streamlines representing the stationary flow field.
Fig. 7.5 Normals χ
∗
to the streamlines ψ
∗
.
7.2.2 Construction of normals
At every point of the horizontal flow field at t = constant streamlines ψ
∗
and
normals χ
∗
form an orthogonal system. Since the instantaneous velocity vector is
tangential to the streamlines, the differential equation of the normals must be given
by
v
h
· dr
N
= 0orudx+ vdy = 0(7.30)
where dr
N
is a line element along the normal; see Figure 7.5.
Equation (7.30) is a total differential of the normal χ
∗
if the integrability condition
∂v
∂x
=
∂u
∂y
(7.31)
is satisfied or if the vorticity ζ is zero. In this case we may write
dχ
∗
=
∂χ
∗
∂x
dx +
∂χ
∗
∂y
dy = udx + vdy = 0(7.32)

7.3 Streamlines in a drifting coordinate system 225
Fig. 7.6 The drifting coordinate system.
from which it follows that
u =
∂χ
∗
∂x
,v=
∂χ
∗
∂y
or v
h
=∇
h
χ
∗
(7.33)
From this equation we may find analytic expressions for the normals in the same
way as that in which we have found stream functions. A comparison with (7.9)
shows that χ
∗
is identical with the velocity potential. If the integrability condition
(7.31) is not satisfied we may introduce an integrating factor and proceed analo-
gously to finding streamlines; see equations (7.22)–(7.25). In this case the normal
χ
∗
will not coincide with the velocity potential χ .
7.3 Streamlines in a drifting coordinate system
We consider a horizontal pressure disturbance φ, which is displaced with phase
velocity c in the eastward direction. The air particles themselves move with the
horizontal velocities v
h
and v
h
with respect to the stationary (x, y)- and the moving
(x
,y
)-coordinate system, see Figure 7.6.
On replacing in the addition theorem of the velocities (M4.32) the velocity v
P
of the moving system by c and the relative velocity v by v
h
,wefind
v
h
= v
h
+ c (7.34)
Application of Euler’s development gives for the resting system the local change
with time of the field function
∂φ
∂t
x,y
=
dφ
dt
− v
h
·∇
h
φ (7.35)
In the moving (x
,y
) system we find
∂φ
∂t
x
,y
=
dφ
dt
− v
h
·∇
h
φ (7.36)

226 Kinematics of two-dimensional flow
Since the individual change with time dφ/dt is independent of the coordinate
system, it may be eliminated by subtracting (7.35) from (7.36), yielding
∂φ
∂t
x,y
=
∂φ
∂t
x
y
− c ·∇
h
φ (7.37)
This relation expresses the local change with time of the function φ in both systems,
which involves, as should be expected, the displacement velocity c.Thelocal
change with time (∂φ/∂t)
x
,y
in the moving system represents the development
of the pressure system. In case of stationarity in the moving system, there is no
development and (∂φ/∂t)
x
,y
= 0.
Next we consider a system of streamlines moving with the phase velocity c in
the direction of the positive x-axis. We assume that the velocity components are
given by
u = U = constant,v=−kA sin[k(x − ct)] (7.38)
Substitution of (7.38) into the streamline equation (7.17), integrating for fixed time
t = t
0
, gives the streamline representation
y =
A
U
cos[k(x − ct
0
)] + constant (7.39)
The question of the shape of the streamlines in the moving system now arises.
The coordinate relation between the two systems is taken from Figure 7.6 but now
we assume that the y-andthey
-axis coincide, or
x
= x − ct, y
= y (7.40)
From this it follows immediately that
u
=
dx
dt
=
dx
dt
− c = U − c, v
=
dy
dt
= v =−kA sin(kx
)
(7.41)
Inspection of (7.41) shows that the velocity field (u
,v
)inthe(x
,y
)systemis
time-independent or stationary. The differential equation of the streamline in the
moving system is then given by
dy
dx
=
v
u
=
v
U − c
=
−kA sin(kx
)
U − c
(7.42)
Integration of (7.42) gives the equation of the streamline of the moving system:
y
=
A
U − c
cos[k(x − ct)] + constant (7.43)
7.3 Streamlines in a drifting coordinate system 227
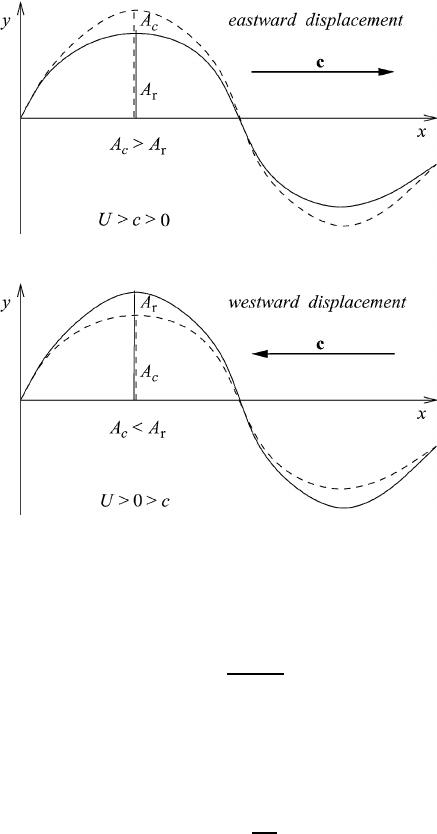
Fig. 7.7 Eastward and westward displacement of the streamline system.
From (7.39) and (7.43) we find the relationship between the amplitudes of the
system at rest (A
r
= A/U) and the moving system [A
c
= A/(U − c)],
A
c
= A
r
U
U − c
(7.44)
Since the wavelength is the same for the streamlines of both systems, we may
arrange the streamlines as shown in Figure 7.7.
On solving (7.44) for the phase velocity c we, find
c = U
1 −
A
r
A
c
(7.45)
In case of an eastward displacement of the streamline system we have A
c
>A
r
,
and A
c
<A
r
for the displacement in the opposite direction.
We conclude this section by giving an example pertaining to the moving co-
ordinate system. We shall assume that the potential temperature is a conservative
quantity during the motion so that
˙
$ = 0. Furthermore, we shall assume stationar-
ity in the moving system. Therefore, the development term (∂$/∂t)
x
,y
= 0 and,
analogously to (7.36), we find
v
h
·∇
h
θ = 0(7.46)
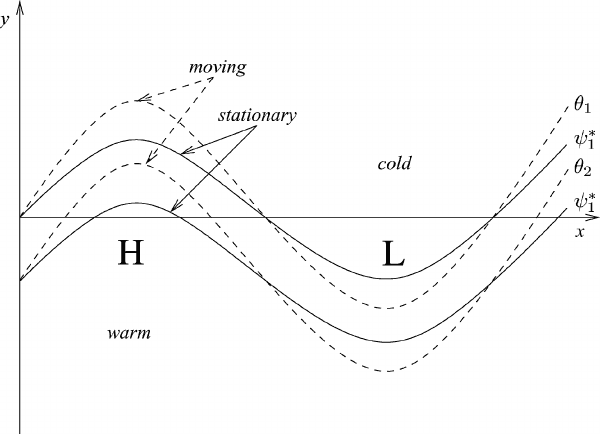
228 Kinematics of two-dimensional flow
Fig. 7.8 Interpretation of relative streamlines, ψ
∗
2
>ψ
∗
1
.
This means that lines of constant potential temperature are arranged parallel to the
horizontal velocity v
h
that is parallel to the streamlines (ψ
∗
)
of the moving system.
In the system at rest, assuming geostrophic conditions, the streamlines ψ
∗
= φ /f
correspond to lines of constant geopotential on an isobaric surface p = constant.
In the tropospheric westward drift most frequently U>c>0. According to (7.44)
the amplitudes of the streamlines in the moving system exceed the amplitudes in
thesystematrestsothatA
c
>A
r
, as shown in Figure 7.8.
By relabeling the relative streamlines (ψ
∗
)
as lines of constant potential tem-
perature we find that moving troughs are colder than moving ridges.
7.4 Problems
7.1: Consider two-dimensional potential flow in a polar coordinate system.
(a) Find the components v
r
and v
t
where r and t refer to the radial and the tangential
direction.
(b) Find the continuity equation for incompressible flow in the polar coordinate
system.
7.2: The circulation is defined by
C =
L
v · dr
7.4 Problems 229
where L is the length of an arbitrary arc. Find the circulation in terms of potential
flow.
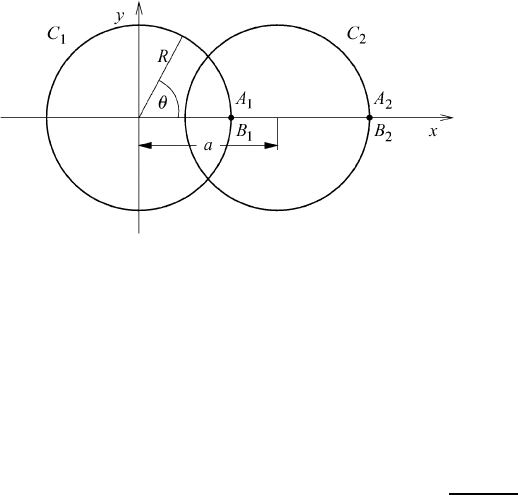
7.3: Suppose that the potential flow is expressed by χ = θ,whereθ is the angle
shown in the figure.
(a) Calculate the circulation along the circle C
1
.
(b) Calculate the circulation along the circle C
2
defined by (x −a)
2
+y
2
= R
2
,a>
R.
7.4: The velocity potential is assum
ed to be given by
χ = ax + by,wherea and
b are real numbers.
(a) Find the total velocity of the flow field.
(b) Find the stream function of the flow field.
7.5: Assuming that the velocity potential is in the form χ = ln
x
2
+ y
2
,show
that the stream function is given by ψ =−arctan(x/y) if we ignore an arbitrary
constant.

8
Natural coordinates
8.1 Introduction
In this chapter we consider horizontal and frictionless flow in a Cartesian coordinate
system on a plane tangential to the earth’s surface as explained in Section 2.5. For
convenience we repeat the equations required for the horizontal wind field:
du
dt
= fv−
1
ρ
∂p
∂x
,
dv
dt
=−fu−
1
ρ
∂p
∂y
(8.1)
The Cartesian system will then be transformed into the natural coordinate system.
The orientation of this system is described by the unit vector e
s
defining the direction
of the horizontal wind vector v
h
=
|
v
h
|
e
s
and the orthogonal unit vector e
n
in the
direction of lines normal to the streamline (normals). To complete the coordinate
system we define the unit vector e
z
in the direction normal to the tangent plane.
Figure 8.1 refers to a section of the horizontal flow field and shows the trajectory
T of a particle at the positions P
T
(t
0
)andP
T
(t
1
)attimest
0
and t
1
. At these locations
the horizontal velocity is given by v
h
(t
0
)andv
h
(t
1
). As described in Section 3.4, the
velocity vector is jointly tangential to the streamline and to the trajectory. While
the trajectory defines a sequence of particle positions, both streamlines and their
normals refer to fixed time. The infinitesimal arclengths s
T
, s and n of the
trajectory T , the streamline S, and the normal N together with the contingency
angle α between e
s
and the x-axis define the corresponding radii of curvature as
given by
R
T
=
ds
T
dα
,R
s
=
∂s
∂α
t
,R
n
=
∂n
∂α
t
(8.2)
Inspection of Figure 8.1 also shows that dR
s
=−dn and dR
n
= ds as n and s
shrink to zero. Since the flow is assumed to be horizontal, the natural coordinate
system is particularly simple and the contingency angles play the dominating
role. Since the coordinate lines s = constant and n = constant are defined only
230
