Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

4.1 The velocity dyadic 191
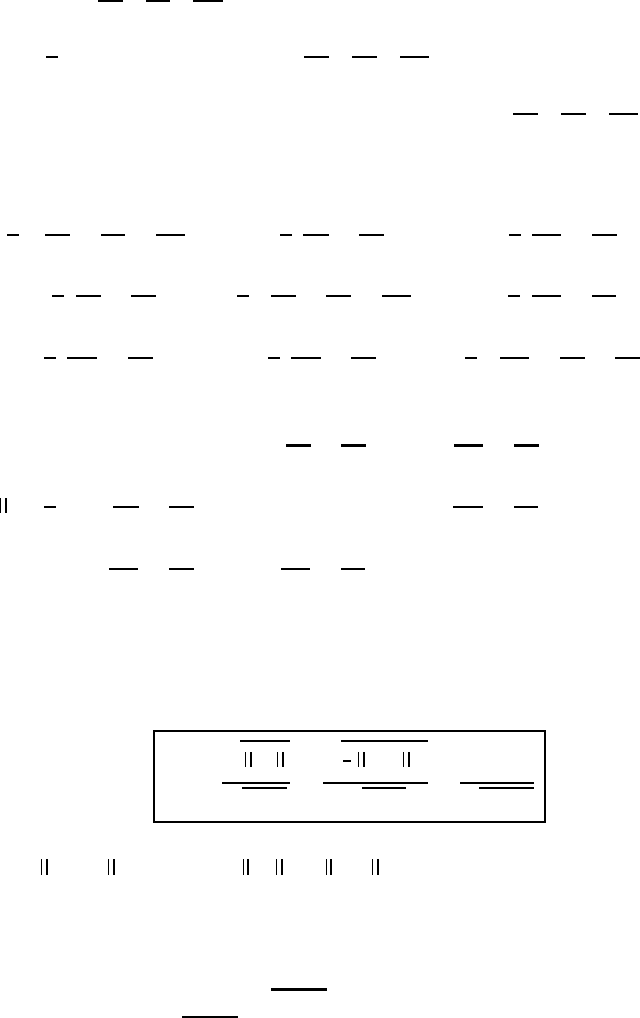
D
i
=
1
3
∂u
∂x
+
∂v
∂y
+
∂w
∂z
ii +0 +0
+0 +
∂u
∂x
+
∂v
∂y
+
∂w
∂z
jj +0
+0 +0 +
∂u
∂x
+
∂v
∂y
+
∂w
∂z
kk
D
ai
=
1
3
2
∂u
∂x
−
∂v
∂y
−
∂w
∂z
ii +
1
2
∂v
∂x
+
∂u
∂y
ij +
1
2
∂w
∂x
+
∂u
∂z
ik
+
1
2
∂v
∂x
+
∂u
∂y
ji +
1
3
2
∂v
∂y
−
∂u
∂x
−
∂w
∂z
jj +
1
2
∂w
∂y
+
∂v
∂z
jk
+
1
2
∂w
∂x
+
∂u
∂z
ki +
1
2
∂w
∂y
+
∂v
∂z
kj +
1
3
2
∂w
∂z
−
∂u
∂x
−
∂v
∂y
kk
=
1
2
0 +
∂v
∂x
−
∂u
∂y
ij +
∂w
∂x
−
∂u
∂z
ik
−
∂v
∂x
−
∂u
∂y
ji +0 +
∂w
∂y
−
∂v
∂z
jk
−
∂w
∂x
−
∂u
∂z
ki −
∂w
∂y
−
∂v
∂z
kj +0
(4.5)
For ease of reference we have explicitly stated all parts.
Before we reduce the previous formulas to the two-dimensional case, we wish
to introduce an important definition known as the kinematic vorticity, ζ
kin
,
ζ
kin
=
··
D··
D
=
1
2
×
·
×
√
D··D
=
|
∇×v
|
√
2D··D
(4.6)
with
=−
, D =
D and ··
=
×
·
×
/2 = (∇×v)
2
/2. ζ
kin
is a measure
of the rigidity of the motion since it involves the deformation dyadic D. Obviously
we may define three limiting cases, given by
ζ
kin
=
0
|
∇×v
|
= 0 vortex-free deformation flow
1
|
∇×v
|
=
√
2D··D rotation equals deformation
∞
√
2D··D = 0 vortex flow without deformation
(4.7)
which characterize the flow field.
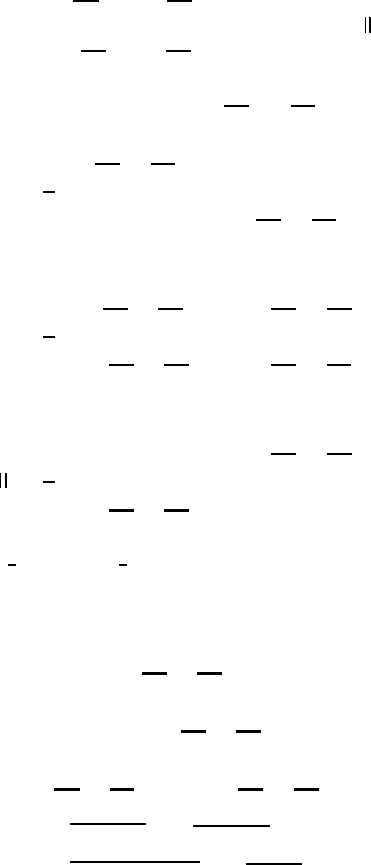
192 Atmospheric flow fields
4.1.2 The two-dimensional velocity dyadic
Inspection of equation (4.5) shows that the horizontal velocity dyadic simplifies to
∇
h
v
h
=
∂u
∂x
ii +
∂v
∂x
ij
+
∂u
∂y
ji +
∂v
∂y
jj
=
D
i
+ D
ai
+
with v
h
= ui + vj, ∇
h
= i
∂
∂x
+ j
∂
∂y
D
i
=
1
2
∂u
∂x
+
∂v
∂y
ii +0
+0 +
∂u
∂x
+
∂v
∂y
jj
D
ai
=
1
2
∂u
∂x
−
∂v
∂y
ii +
∂u
∂y
+
∂v
∂x
ij
+
∂u
∂y
+
∂v
∂x
ji −
∂u
∂x
−
∂v
∂y
jj
=
1
2
0 +
∂v
∂x
−
∂u
∂y
ij
−
∂v
∂x
−
∂u
∂y
ji +0
(4.8)
Note that the factor
1
2
instead of
1
3
appears in the deformation dyadic D
i
since the
first scalar of the two-dimensional unit dyadic is 2. Various combinations of partial
derivatives appear, which will be abbreviated as
(a) D =∇
h
· v
h
=
∂u
∂x
+
∂v
∂y
(b) ζ = k ·∇
h
× v
h
=
∂v
∂x
−
∂u
∂y
=⇒ ∇
h
× v
h
= kζ
(c) A =
∂u
∂x
−
∂v
∂y
,B=
∂u
∂y
+
∂v
∂x
(d) def =
A
2
+ B
2
=
2D
ai
··D
ai
(e) Def =
A
2
+ B
2
+ D
2
=
√
2D··D
(4.9)
The symbols D and ζ denote the two-dimensional divergences of the horizontal
velocity field and the vorticity, respectively. The quantities A and B of (4.9c) are
known as the principal parts of the deformation field. Some geometric interpreta-
tions will be given at the end of this chapter. It should be noted that the quantities
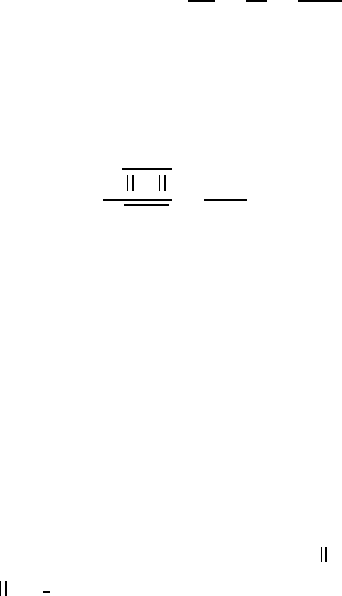
4.2 The deformation of the continuum 193
D, ζ, etc. were introduced without reference to the rotating earth. If the rotation
of the earth needs to be accounted for, we would have to allow for certain modifi-
cations. For example, the vorticity ζ would have to be replaced by ζ + f . Details
will be given in a later chapter.
Recall that any dyadic is an extensive quantity that is independent of a particular
coordinate system. If the general multiplication in dyadic products is replaced by the
vectorial or the scalar multiplication new quantities are produced, which are again
independent of the coordinate system. Such quantities are known as invariants. D
and ζ are invariants whereas A and B are not. Furthermore, the velocity deformation
fields def and Def , given in (4.9d) and (4.9e), are also invariants because of the
double scalar products involved in these terms. The various invariants of the local
two-dimensional velocity dyadic are listed next:
First scalar: (∇
h
v
h
)
I
=∇
h
· v
h
= D
Vector: (∇
h
v
h
)
×
=∇
h
× v
h
= kζ
Second scalar: (∇
h
v
h
)
II
= J (u, v) =
D
2
4
+
ζ
2
4
−
def
2
4
Third scalar: (∇
h
v
h
)
III
= J (u, v)
(4.10)
Note that, in the two-dimensional case, the second and the third scalar are identical.
In analogy to the three-dimensional case (4.6) we define the two-dimensional
kinematic vorticity
ζ
kin
=
√
··
√
D··D
=
ζ
Def
(4.11)
Thus, ζ
kin
is the ratio of two invariants. We shall not discuss this concept in more
detail.
4.2 The deformation of the continuum
4.2.1 The representation of the wind field
We consider the structure of the wind field at a fixed time in the infinitesimal
surroundings of a point P as shown in Figure 4.1. In the immediate neighborhood
at point P
we may write
v(P
) = v(P ) + δr ·∇v(P )
= v(P ) + δr · D
i
+ δr · D
ai
+ δr ·
with δr · =
1
2
(∇×v) × δr = Ω × δr
(4.12)
where we have discontinued the Taylor expansion after the linear term. In (4.12)
we have introduced the local velocity dyadic ∇v which is considered a constant
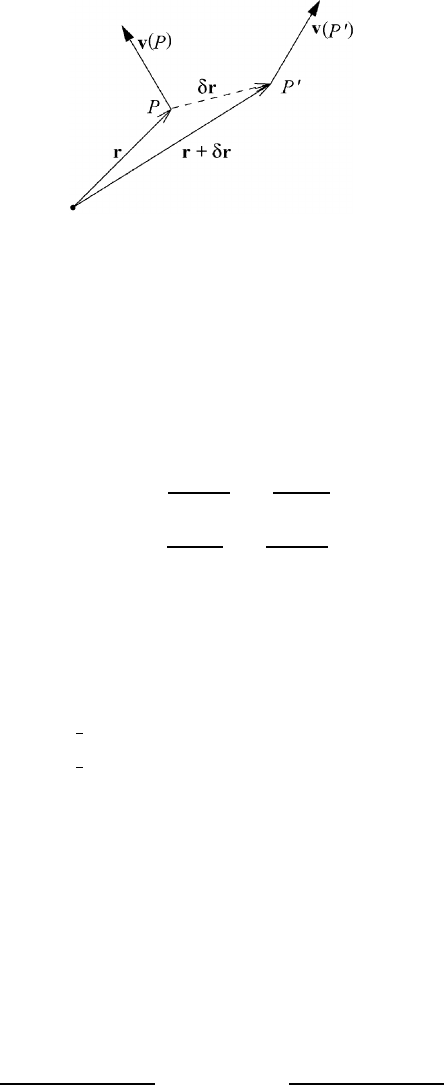
194 Atmospheric flow fields
Fig. 4.1 A representation of the wind field.
quantity in the immediate neighborhood of P .Thevelocityv(P
) consists of two
parts. v(P ) represents the joint translation of the two points while
δr ·∇v(P )isthe
velocity of point P
relative to P . The vector Ω represents the angular velocity of
a rigid rotation of P
about an axis through P .
By carrying out the scalar multiplication in (4.12) and using the definitions (4.9),
we immediately find the component form of the two-dimensional wind field:
u = u
0
+
A + D
2
x +
B − ζ
2
y
v = v
0
+
B + ζ
2
x +
D − A
2
y
(4.13)
where the suffix 0 represents the velocity components at point P . Moreover, we
have replaced
δx and δy by x and y.
We have previously stated that A
2
+ B
2
is an invariant. By axis rotation this
allows us to take A>0andB = 0sothat∂u/∂y =−∂v/∂x. Thus (4.13) reduces
to
u = u
0
+
1
2
(Ax + Dx − ζy) = u
0
+ u
1
+ u
2
+ u
3
v = v
0
+
1
2
(−Ay + Dy + ζx) = v
0
+ v
1
+ v
2
+ v
3
(4.14)
The various velocity components appearing in this equation denote the following
types of linear flow field near the point P :(u
0
,v
0
): translation, (u
1
,v
1
): defor-
mation, (u
2
,v
2
): divergence, (u
3
,v
3
): rotation. These flow types are taken from
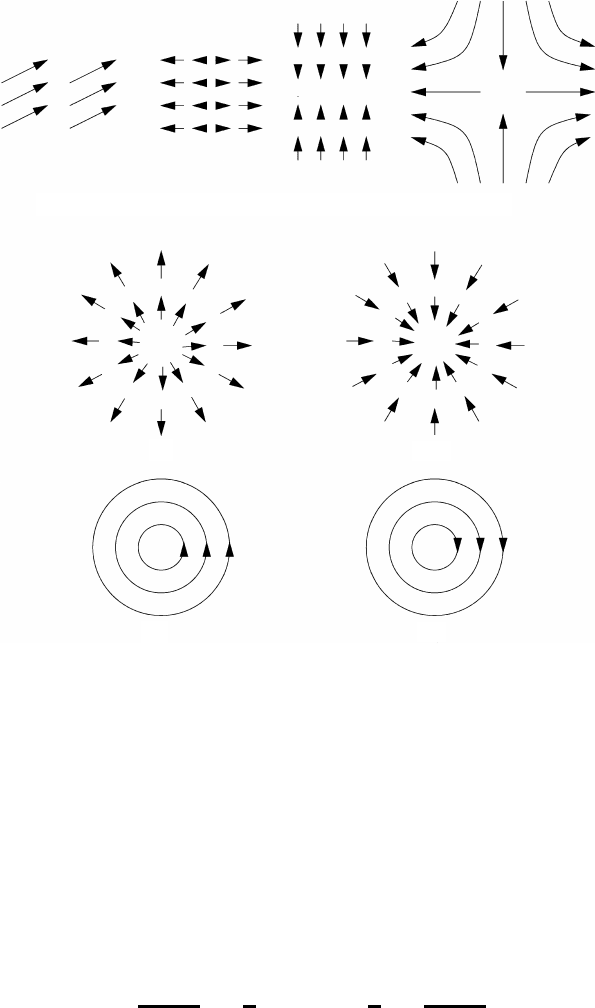
Petterssen (1956) or Panchev (1985) and are depicted in Figure 4.2.
The x-andy-components of the deformation field are known as dilatation and
contraction, respectively. We will now determine the coordinates (x
c
,y
c
)ofthe
so-called kinematic center, which is a point where the velocity vanishes. By setting
u = v = 0 in (4.14) and then solving for the coordinates x = x
c
and y = y
c
of the
system we find
x
c
=−2
u
0
(D − A) + v
0
ζ
D
2
− A
2
+ ζ
2
,y
c
=−2
v
0
(D + A) − u
0
ζ
D
2
− A
2
+ ζ
2
(4.15)
4.2 The deformation of the continuum 195
(a) (b) (c) (d)
(e)
(f )
(h)
(g)
Fig. 4.2 Component motions of the linear flow field: (a) uniform translation, (b) and (c)
deformation, (d) total deformation, (e) divergence, (f ) convergence, (g) positive rotation–
idealized northern-hemispheric low-pressure system, and (h) negative rotation–idealized
northern-hemispheric high-pressure system.
The condition for the existence of a kinematic center may therefore be written as
D
2
− A
2
+ ζ
2
= 0(4.16)
On translating the origin of the coordinate system to the kinematic center,
equation (4.14) reduces to
u =
D + A
2
x −
ζ
2
y, v =
ζ
2
x +
D − A
2
y (4.17)
The question of whether there are straight streamlines through the center arises quite
naturally. If the streamlines are to be straight, then the equation of the streamline
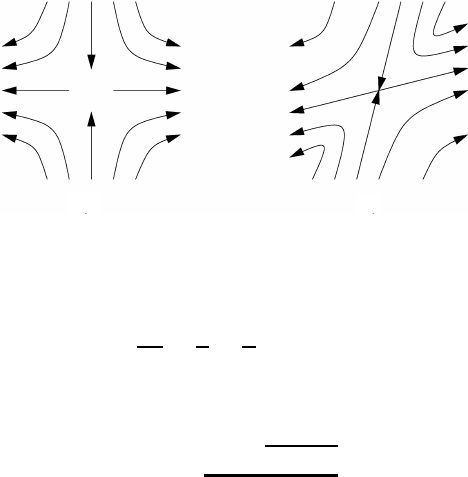
196 Atmospheric flow fields
(a) (b)
Fig. 4.3 Hyperbolic streamline patterns describing deformation: (a) pure deformation, and
(b) with added rotation.
can be written as
dy
dx
=
v
u
=
y
x
= tan ϑ (4.18)
where ϑ is the angle between the x-axis and the streamline.
On substituting from (4.17) we obtain
tan ϑ =
A ±
A
2
− ζ
2
ζ
(4.19)
First of all we note that the angle is independent of the divergence D. Analyzing
equation (4.19) leads to the following conclusions.
(i) If A = ζ = 0 we have pure divergence. In this unrealistic case an infinite number of
straight streamlines will pass through the center, see Figures 4.2(e) and 4.2(f ).
(ii) If A>ζthen the deformative component exceeds the rotational part. In this case
there are two roots so that two streamlines pass through the center dividing the plane
into four sectors. In each sector the streamlines are of the hyperbolic type, as shown
in Figure 4.3, where two idealized cases are presented.
(iii) If A
2
<ζ
2
then there are no real solutions for β. Consequently, there will be no straight
streamlines passing through the center. Typical situations for this case are shown in
Figure 4.4.
4.2.2 Flow patterns and stability
We conclude this section by looking at the flow pattern from the modern point of
view involving elementary stability theory. For more details see also Section M7.2.
We proceed by writing equation (4.17) in the form
˙x = ax + by = X(x,y), ˙y = cx + dy = Y (x, y)(4.20)
The parameters a, b,c,andd can be identified by comparison with (4.17). Be-
ginning at an arbitrary initial point, the solution x(t),y(t) of (4.20) traces out a
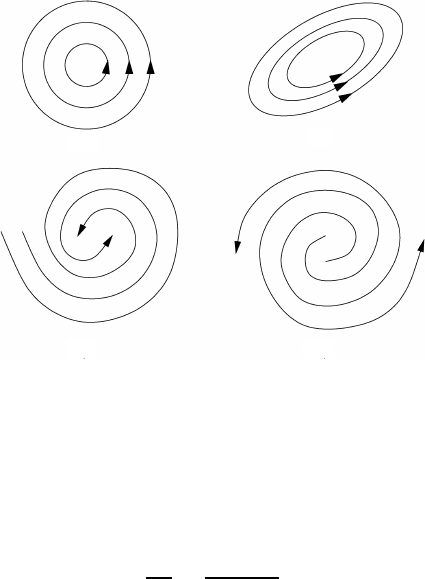
4.2 The deformation of the continuum 197
(a)
(d)
(c)
(b)
Fig. 4.4 Flow pat
terns without straight streamlines: (a) pure rotation, (b) rotation and
deformation, (c) convergence superimposed on (b), and (d) divergence superimposed on
(b); (a) and (b) are also called centers whereas (c) and (d) are known as spirals.
directed curve in the (x,y)-plane which is known as the phase path. From (4.20)
we may easily form the streamline equation, which can always be solved:
dy
dx
=
cx + dy
ax + by
(4.21)
Let us consider the fixed point (x
∗
,y
∗
) satisfying the relations
X(x
∗
,y
∗
) = 0,Y(x
∗
,y
∗
) = 0(4.22)
This point determines the qualitative behavior of the solution. It is convenient to
write (4.20) in matrix form:
˙
x = F x, x =
x
y
,F=
ab
cd
(4.23)
According to (M7.11), the general solution to (4.20) is given by
x(t) = C
1
x
1
exp(λ
1
t) + C
2
x
2
exp(λ
2
t)(4.24)
where the λ
i
are the eigenvalues or the characteristic values of the matrix F and
the x
i
are the corresponding eigenvectors. The eigenvalues are found from the
characteristic equation
a − λb
cd− λ
= 0(4.25)

198 Atmospheric flow fields
The expanded form can be written as
λ
2
− τλ+ $ = 0
with τ = trace(F ) = a + d = λ
1
+ λ
2
$ =
|
F
|
= ad − bc = λ
1
λ
2
λ
1,2
=
τ ±
√
τ
2
− 4$
2
(4.26)
Let us consider one more example. For the matrix
F =
11
4 −2
(4.27a)
we find the eigenvalues and eigenvectors
λ
1
= 2, x
1
=
x
1
y
1
=
1
1
λ
2
=−3, x
2
=
x
2
y
2
=
1
−4
(4.27b)
so that the formal solution (4.24) is given by
x = C
1
1
1
exp(2t) + C
2
1
−4
exp(−3t)(4.28)
The eigenvectors may also be multiplied by a constant factor, which could be ab-
sorbed by the integration constants. The eigensolution corresponding to λ
1
grows
exponentially while the second eigensolution decays, meaning that the origin is a
saddle point. The stable manifold is the line spanned by the eigenvector multiply-
ing exp(−3t) while the unstable manifold is the line spanned by the eigenvector
multiplying exp(2t). To get a better impression of the flow field we have included
additional trajectories by continuity, as is qualitatively shown in Figure 4.5. The
similarity to Figure 4.3(b) is apparent.
The fixed points may be classified according to the simple scheme shown in
Figure M7.13. Since $ =−6 the solution is a saddle point.
Fig. 4.5 Trajectories of the example given by equation (4.28).
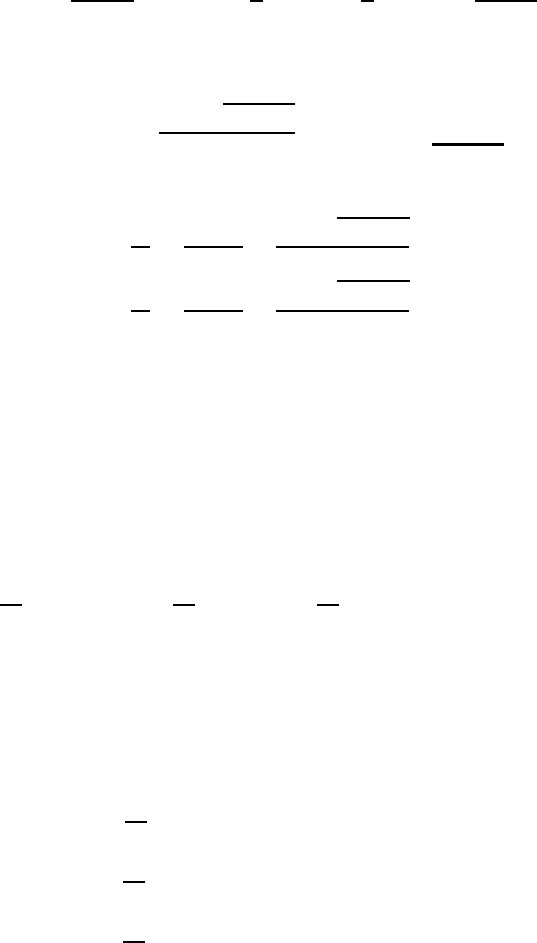
4.3 Individual changes with time of geometric fluid configurations 199
It may be recognized that the information content of equation (4.19) and the
information expressed by the two-dimensional eigenvectors are equivalent. To
show this, we identify the parameters a, b,c,andd by comparison of (4.17) and
(4.20). The result is
a =
D + A
2
,b=−
ζ
2
,c=
ζ
2
,d=
D − A
2
(4.29)
With this identification we easily find the eigenvalues and the eigenvectors of the
flow system (4.17) as
λ
1,2
=
D ±
A
2
− ζ
2
2
, x
1,2
=
1
λ
1,2
− a
b
(4.30)
On taking the ratio of the components of the eigenvectors we again obtain (4.19),
y
1
x
1
=
λ
1
− a
b
=
A −
A
2
− ζ
2
ζ
= tan ϑ
1
y
2
x
2
=
λ
2
− a
b
=
A +
A
2
− ζ
2
ζ
= tan ϑ
2
(4.31)
We should not have expected anything else since the two ways of characterizing
the flow are equivalent.
4.3 Individual changes with time of geometric fluid configurations
We will now derive expressions for time changes of fluid elements (moving lines,
surfaces, volumes). Let us consider a small line element
δr. Replacing in (M6.47)
the vector A by the unit dyadic
E we find immediately
d
dt
L(t)
dr · E
=
d
dt
L(t)
dr
=
d
dt
(δr) =
L(t)
dr · (∇v · E)
=
L(t)
dr ·∇v = δr ·∇v with
L(t)
dr = δr
(4.32)
Similarly we proceed in case of a surface and a volume. The corresponding ex-
pressions are obtained by replacing A in (M6.53) by
E and by setting ψ = 1in
(M6.57). The results are collected in
(a)
d
dt
(
δr) = δr ·∇v,
L(t)
dr = δr
(b)
d
dt
(
δS) = δS ∇·v −∇v·δS,
$S(t)
dS = δS
(c)
d
dt
(
δτ ) = δτ ∇·v,
$V (t)
dτ = δτ
(4.33)
200 Atmospheric flow fields
Here the terms ∇v and ∇·v have been treated as constants. We should keep in
mind that these expressions are only approximate. However, for most practical
purposes they are sufficiently accurate. If the initial configurations of δr, δS,and
δτ are known, then the deformations of the fluid elements can be calculated by
means of time integration.
In the next section we discuss various geometric properties resulting from the
application of the local dyadic. Using as an example the liquid or material line
element in the flow field, we find from (4.33a) and (4.5)
d
dt
(
δr) = δr ·∇v = δr ·D −
1
2
δr ·E ×(∇×v) = δr ·D
i
+δr ·D
ai
+
1
2
(∇×v) ×
δr
(4.34)
where
δr = δr e and e is a unit vector in the direction of δr. Several special cases
that can easily be comprehended arise.
4.3.1 The relative change of the material line element
The following manipulation of the relative change
δr is obvious:
1
δr
d
dt
(
δr) =
1
(δr)
2
d
dt
(
δr)
2
2
=
1
(δr)
2
d
dt
(
δr)
2
2
=
1
(δr)
2
δr ·
d
dt
(
δr)
(4.35)
On substituting from (4.33a) we obtain immediately for the relative change
1
δr
d
dt
(
δr) =
1
(δr)
2
(δr ·∇v · δr) = e ·∇v · e (4.36)
or
1
δr
d
dt
(
δr) = e · D · e since e ·
(∇×v)
2
× e = 0(4.37)
Therefore, the relative change with time of the material line element depends only
on the symmetric part of the local dyadic, which is equivalent to the deformation
dyadic. This means that the antisymmetric part of the local velocity dyadic does
not contribute to the relative change.
4.3.2 The directional change of the material line element
If we wish to determine the directional change of the line element we must also
consider the change with time of the unit vector, or
d
dt
(
δr) = δr
de
dt
+ e
d
dt
(
δr)(4.38)
