Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology

Подождите немного. Документ загружается.

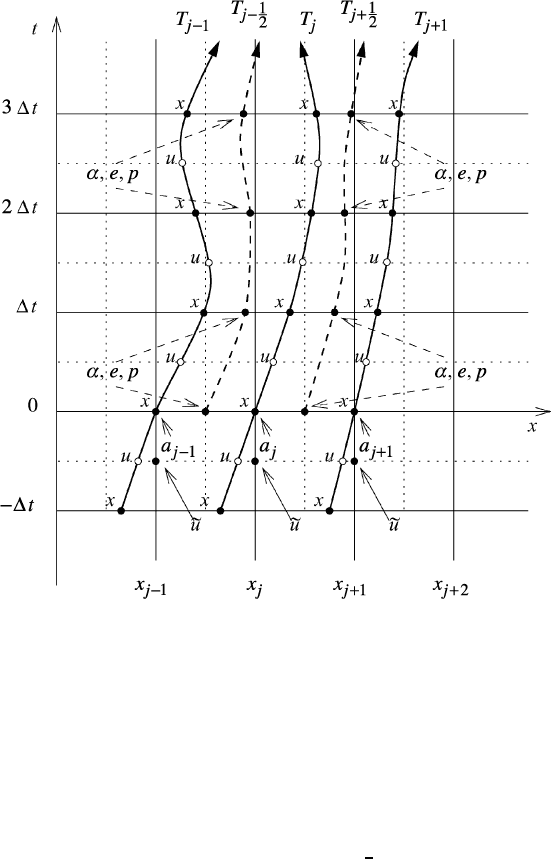
3.3 An example of the use of Lagrangian coordinates 181

Fig. 3.6 Schematic results for the state variables u, α, e, p,andx(a,t). T

and T

j±1

are the

calculated trajectories of particles a

j±1

while T

j±1/2

are the interpolated trajectories

of particles a

j±1/2

3.3.4.2 The interpolated velocity u

−1/2

on the trajectory

By means of a straight-line interpolation in the backward direction the trajectory

point T

at time −t/2 is approximated as

x

−1/2

= x(a

, −t/2) = x

−



x

− x



(3.34)

Now the required starting value u

−1/2

can be found from interpolation so that

−1/2

= u(x

−1/2

, −t/2) (3.35)

Now the so-far-missing values of the velocity u are known and the procedure

(3.32a)–(3.32f) can be used to ﬁnd the solution, provided that the boundary condi-

tions are known.

182 The material and the local description of ﬂow

Table 3.1. Arrangements of variables for Euler and Lagrange schemes

Scheme Independent variables Dependent variables Examples

= a

,t) v(x

,t)

Euler x

,t a

= a

,t)

[v(x

,t)]

= a

,t)

= x

,t) v(a

,t)

Lagrange a

,t x

= x

,t)

∂

∂t

[v(a

,t)]

= x

,t)

Typical boundary conditions at j = J may be speciﬁed as follows:

rigid wall: u

n±1/2

= 0foralln,

free surface: p

J +1/2

=−p

J −1/2

for all n.

The latter boundary condition has the effect that the interpolated value of p vanishes

at j = J .

3.3.5 The numerical stability condition

The numerical solution of the present problem requires that the Courant–Friedrichs–

Lewy stability criterion be obeyed. The Cartesian form of this criterion is given

t

x

≤ 1(3.36)

Using (3.28) we ﬁnd

t ≤

αa

(3.37)

where the isentropic velocity of sound c is determined by (3.21).

3.4 The local description of Euler

The description of ﬂuid motion according to Euler requires knowledge of the

velocity ﬁeld at ﬁxed points within the ﬂuid. If measurements of the velocity are

carried out simultaneously at many points then we obtain a spatial picture of the

ﬂow.

The descriptions of the ﬂuid according to the methods of Lagrange and Eu-

ler require different variables. The reciprocal arrangement of the dependent and

independent variables is listed in Table 3.1.

3.4 The local description of Euler 183

Fig. 3.7 A two-dimensional ﬂow ﬁeld and representative streamlines, t = t

Figure 3.7, as an example of the Eulerian method, shows a two-dimensional

velocity vector ﬁeld for a ﬁxed time t = t

. This snapshot of the ﬂow ﬁeld will

be used to introduce the important concept of the streamline. A vector line that

is tangential everywhere to the instantaneous wind vector is called a streamline.

The direction of the wind vector is ﬁxed by the unit tangential vector t which is

tangential to the streamline as well as to the trajectory, as stated by the following

equation:

t =



∂r

∂s





∂r

∂σ



Euler Lagrange

(3.38)

It should be noted that different arclengths are used for the Euler (streamline) and

the Lagrange (trajectory) representations.

By deﬁnition, for ﬁxed t = t

, the velocity vector is tangential to every increment

r → 0 of the streamline, so that

dr × v = 0withdr = i

, v = i

u + i

v + i

w (3.39)

From this condition the component forms can be written down immediately,

(a)

w(x

)

v(x

)

(b)

w(x

)

u(x

)

(c)

v(x

)

u(x

)

(3.40)

184 The material and the local description of ﬂow

Only two of these are independent since, for example, division of (3.40b) by

(3.40a) gives (3.40c). The integration of two of these differential equations gives

the parameter represention of the streamline,

) = C

,i= 1, 2,j= 1, 2, 3(3.41)

A simple example will clarify the idea for the case of a horizontal streamline.

We have

= A cos[k(x − ct

)] (3.42)

where k is the wavenumber and c the phase velocity. Integration of (3.42) results

y −

sin[k(x − ct

)] = C (3.43)

Another example will be given shortly.

In contrast to the streamline which refers to the ﬁxed time t = t

, the trajectory,

according to Euler, exhibits an explicit time dependency. The differential equations

specifying the velocity vector v of the trajectory are given by

= v

,t),v

= u, v

= v, v

= w (3.44)

The solution is formally given by

= x

,t)(3.45)

where the integration constants x

are the initial coordinates of the particle of

concern at time t = t

In general, the streamlines and trajectories are different; only for the steady state

do they coincide. The following simple example will demonstrate this. Consider

the motion of a ﬂuid in a vertical plane with

u =

= x + t, w =

=−z + t (3.46)

where we have used the more familiar coordinates (x,z) instead of (x

). Now

ﬁnd

(a) the family of streamlines

and the particular streamline passing through the point

P (x,z) = (−1, −1) at t = t

= 0, and

(b) the trajectory of the particle passing through the same point at t = t

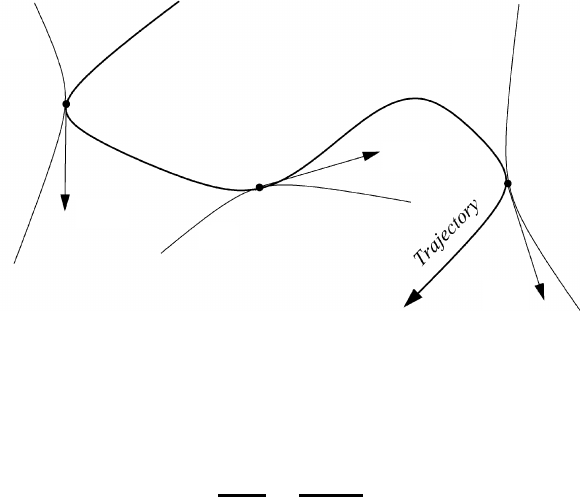
3.4 The local description of Euler 185

s(t

)

v(t

)

s(t

)

v(t

)

s(t

)

v(t

)

Fig. 3.8 The envelope of a system of successive streamlines.

Solution:

(i) The ﬂow is two-dimensional and nonstationary since u and w contain t ex-

plicitly. From (3.46) we obtain

x + t

−z + t

(3.47)

The integration is carried out for t = t

= constant, giving

ln(x + t) =−ln(−z + t) + ln C =⇒ (x + t)(−z + t) = C (3.48)

which is a family of hyperbolas. For t = t

at (x,z) = (−1, −1) we have C =−1

so that the particular streamline passing through the given point is given by

xz = 1(3.49)

(ii) First of all we note that the differential equations are decoupled. The solution

is easily carried out by standard methods, with the result

x = C

exp t − t − 1,z= C

exp(−t) + t − 1(3.50)

from which it follows that C

= C

= 0. Elimination of t gives

x + z =−2(3.51)

which is the equation of a straight line, showing that the trajectory and the stream-

lines do not coincide.

Finally, Figure 3.8 shows that the trajectory of a particle is the envelope of a

system of successive streamlines.

Occasionally, the concept of a streak line, which is a line connecting all the

particles that have passed a given geometric point, is used. A plume of smoke from

a chimney may be viewed as a streak line.

186 The material and the local description of ﬂow

3.5 Transformation from the Eulerian to the Lagrangian system

We consider an arbitrary ﬁeld function ψ in the Cartesian Eulerian x

system and

the Lagrangian a

system, i.e.

Euler: ψ = ψ(x

,t)

Lagrange: ψ = ψ(a

,t)

(3.52)

The gradient operator in these systems is given by

Euler: ∇ψ = i

∂ψ

∂x

Lagrange: ∇ψ = a

∂ψ

∂a

(3.53)

The transformation rules of the partial derivatives as derived in (M4.24) may be

written as

∂ψ

∂a

=∇

ψ =

∂x

∂a

∂ψ

∂x

∂a

∇

∂ψ

∂x

=∇

ψ =

∂a

∂x

∂ψ

∂a

∂x

∇

(3.54)

It may be helpful to rewrite the transformation relations by using matrix notation.



represents the transpose of the transformation matrix T

= (∂x

/∂a

), where

i labels the row and j the column, we may write instead of (3.54)







∂

∂a

∂

∂a

∂

∂a









∂x

∂a









∂

∂x

∂

∂x

∂

∂x















∂

∂x

∂

∂x

∂

∂x







(3.55)

The inverse relation of (3.55), denoted by the overbar, is given by







∂

∂x

∂

∂x

∂

∂x









∂a

∂x









∂

∂a

∂

∂a

∂

∂a















∂

∂a

∂

∂a

∂

∂a







(3.56)

Since (3.55) and (3.56) are inverse relations, we must have















∂x

∂a



∂a

∂x





∂x

∂a

∂x















∂x

∂a



∂a

∂x





∂x

∂a

∂x







(3.57)

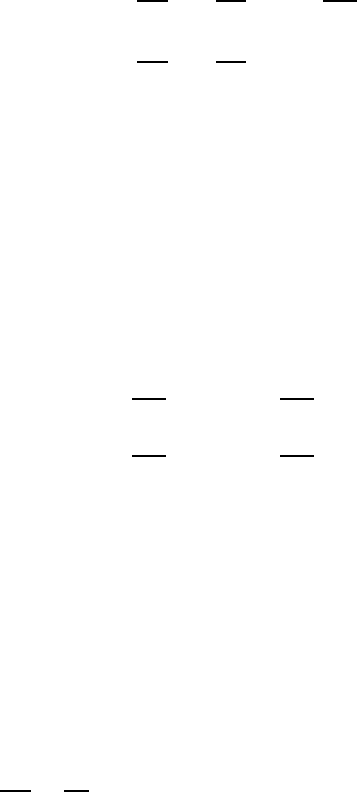
3.6 Problems 187

For completeness we state the individual time derivatives in both systems:

Euler:

dψ



∂ψ

∂t



+ ˙x

∂ψ

∂x

Lagrange:

dψ



∂ψ

∂t



since ˙a

= 0

(3.58)

The individual or material derivative represents the total change of ψ as viewed by

an observer following the ﬂuid particle. The ﬁrst expression of (3.58) is sometimes

called the Lagrangian derivative as expressed in terms of the Eulerian coordinates.

The local derivative (∂ψ/∂t)

i is occasionally called the Eulerian derivative ex-

pressing the change of ψ at any point ﬁxed in space. The term ˙x

∂ψ/∂x

has the

meaning that, in time-independent ﬂows, the ﬂuid properties of ψ depend on the

spatial coordinates only. For further details see, for example, Currie (1974).

We conclude this section by restating the transformation relations for the basis

vectors. These are given by the rules derived in (M4.8) as

∂x

∂a

, i

∂a

∂x

∂a

∂x

, i

∂x

∂a

= i

= x

(3.59)

since in the orthogonal Cartesian system there is no difference between covariant

and contravariant basis vectors and measure numbers.

The equation of relative motion expressed in terms of the Lagrangian enumera-

tion coordinates will be presented later when the necessary background is available.

3.6 Problems

3.1: Starting with the continuity equation in the general coordinate-free form

Dρ

dρ

+ ρ ∇·v

= 0withv

= v + v

prove the validity of equation (3.13).

3.2: Consider a two-dimensional ﬂow ﬁeld described by

u = x(1 + 2t),v= y

(a) Find the equation of the streamline passing through the point (x,y) = (1, 1)

at time t = 0.

(b) Find the equation of the trajectory.

188 The material and the local description of ﬂow

3.3: A particular two-dimensional ﬂow is deﬁned by the velocity components

u = A + Bt, v = C. A, B,andC are constants.

(a) Show that the streamlines are straight lines.

(b) Show that the trajectories are parabolas.

Atmospheric ﬂow ﬁelds

4.1 The velocity dyadic

In this chapter we will recognize that the velocity dyadic is of great importance in the

kinematics of atmospheric motion. First of all we will discuss some general proper-

ties in three dimensions. This will be followed by two-dimensional considerations

since the large-scale atmospheric motion may be considered quasi-horizontal. We

will restrict the discussion to Cartesian coordinates.

4.1.1 The three-dimensional velocity dyadic

As is well known from tensor analysis (see Chapter M2), any dyadic may be written

as the sum of the symmetric and antisymmetric parts

∇v =

+ V

∇v + v



∇

∇v − v



∇

with

= D =

∇v + v



∇

deformation dyadic

=  =

∇v − v



∇

rotation dyadic

(4.1)

The deﬁnitions are general and may be applied to any vector A. Therefore, at this

point it is not necessary to specify whether v refers to relative or absolute motion.

The reason why the symmetric and antisymmetric parts are given the designations

deformation dyadic and rotation dyadic will become obvious shortly. As has already

189

190 Atmospheric ﬂow ﬁelds

been practiced in Section M2.4.1, we will decompose the symmetric deformation

dyadic and ﬁnd

D = D

+ D

with D

∇v + v



∇

−

∇·v

(4.2)

where the sufﬁces ai and i stand for anisotropic and isotropic. Splitting the defor-

mation dyadic is mainly for mathematical convenience since certain operations to

be applied to this dyadic cause some parts to vanish.

The reason why the antisymmetric part of the local velocity dyadic is associated

with the rotational part of the ﬂow ﬁeld can best be demonstrated by recalling the

vector identity (M2.98), which is restated here for a special case

E × (B × C) = E · (CB − BC)(4.3)

On replacing the unspeciﬁed vectors B and C by the gradient operator and the

velocity v, respectively, we obtain

E × (∇×v) =−E ·



∇v − v



∇



=−E ·  =−

(4.4)

thus justifying the name rotation dyadic. Using the above deﬁnitions, the velocity

dyadic can now be written as

∇v =







∂u

∂x

ii +

∂v

∂x

ij +

∂w

∂x

∂u

∂y

ji +

∂v

∂y

jj +

∂w

∂y

∂u

∂z

ki +

∂v

∂z

kj +

∂w

∂z







∇·v

E +



∇v + v



∇

−

∇·v



−

E × (∇×v) = D

+ D

+ 