Zdunkowski W., Bott A. Dynamics of the atmosphere: A course in theoretical meteorology
Подождите немного. Документ загружается.

5.4 The frictional stress tensor and the deformation dyadic 211
On splitting D into its isotropic and anisotropic parts and reverting to the general
form (4.2), we find
J = 2µD
ai
+
2µ
3
− λ
∇·v
A
E (5.17)
We assume that λ and µ do not explicitly depend on the spatial coordinates, i.e.
∇µ = 0, ∇λ = 0(5.18)
However, µ exhibits some dependency on the temperature. Values of µ can be
found in various handbooks. The coefficient (2µ/3 − λ) is known as the co-
efficient of volume viscosity since it multiplies the divergence term in (5.17)
describing the relative changes in volume. In atmospheric systems this coeffi-
cient may be neglected. This statement can be motivated with the help of statistical
thermodynamics. There it is shown that this coefficient is zero for monatomic
molecules so that, to an acceptable approximation, we may write
J = 2µD
ai
(5.19)
We conclude this chapter with a simple example. Consider the symmetric stress
tensor
J defined by (5.19):
J = µ
∇v
A
+ v
A
∇
2
−
2
3
µ ∇·v
A
E (5.20)
We recognize that
J is known at a certain point P if ∇v
A
is known there. Assuming
that the absolute velocity v
A
is given by
v
A
= u(z)i + v(x)j + w(y)k (5.21)
we find ∇·v
A
= 0sothat
J = µ
∂u
∂z
(ki + ik) +
∂v
∂x
(ij + ji) +
∂w
∂y
(jk + kj)
(5.22)
For the viscous surface force p
2
(v
A
) defined by (5.2), we find for different
orientations of the surface unit normal
n = i : p
2
(v
A
) = i · J = µ
∂u
∂z
k +
∂v
∂x
j
n = j : p
2
(v
A
) = j · J = µ
∂v
∂x
i +
∂w
∂y
k
n = k : p
2
(v
A
) = k · J = µ
∂u
∂z
i +
∂w
∂y
j
(5.23)
For n = i the surface force at P has the orientation shown in Figure 5.2.
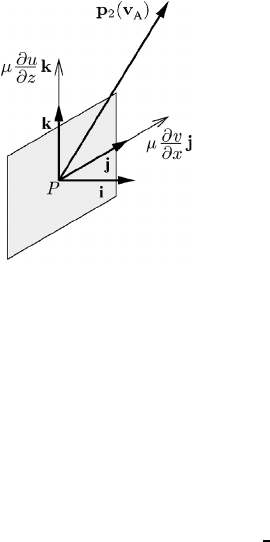
212 The Navier–Stokes stress tensor
Fig. 5.2 The viscous force for n = i. p
2
(v
A
) at point P results from the addition of the
two vectors in the j-andk-directions.
5.5 Problems
5.1: Assuming the validity of (5.19) and µ = constant, find an expression for the
term ∇·
J.
5.2: Show that
v
A
·∇·J =∇·(v
A
· J) −∇v
A
··J
with (a) v
A
· J = µ[∇v
2
A
+ (∇×v
A
) × v
A
−
2
3
(∇·v
A
)v
A
]
(b) ∇v
A
··J = 2µD
ai
··D
ai
= ρ
The quantity is the Rayleigh dissipation function, which is a source term for the
internal energy and a sink term for the kinetic energy.
5.3: Assume that we have incompressible two-dimensional and steady flow on an
inclined plane of infinite extent. The x-axis lies in the plane and the z-direction is
perpendicular to it. Thus, we have v = 0,w = 0,∂/∂y = 0,∂/∂t = 0.
(a) Find an expression for the profile of the velocity u in the x-direction using the boundary
conditions u(z = 0) = 0and(∂u/∂z)
z=H
= 0. Ignore Coriolis effects. Hint: Return to
equation (1.60) with v
D
= 0.
(b) What is the orientation of the isobars?
(c) Find the amount of fluid q per unit time and uni
twidth
flowing between z = 0and
z = H .
(d) Find the energy dissipation ρ within the channel.
5.4: Assume that we have incompressible two-dimensional and steady flow
between two parallel plates. The lower plate is at rest. Ignore Coriolis effects.
(a) Suppose that the upper plate at z = H is moving with the velocity u(z = H )inthe
x-direction. Starting with equation (1.60), show that a linear velocity profile will form.
This flow is known as the Couette flow. The lower boundary condition is u(z = 0) = 0.
5.5 Problems 213
(b) In contrast to part (a), assume now that both plates are at rest, but a
pressure gradient −(1/ρ)(∂p/∂x) is admitted. This is known as Poiseuille flow.The
boundary conditions are u(z = 0) = 0,u(z = H ) = 0.
5.5: Assume that the flow field is proportional to the position vector, that is v
A
=
Cr. The constant of proportionality C carries the units per second. Find the stress
tensor J, the force due to viscous stress p
2
(v
A
), and the tensor ellipsoid.
6
The Helmholtz theorem
6.1 The three-dimensional Helmholtz theorem
If within a region of interest the divergence ∇·v and the rotation ∇×v of the
velocity vector v are given and if these vanish sufficiently fast on approaching
infinity, then v is uniquely specified. More generally we may state:
Every vector field v whose divergence and rotation possess potentials
can be written as the sum of a divergence-free vector field plus another
vector field that is irrotational.
We will now proceed with the proof by assuming that the vector v can be written
as the sum of two vectors such that the rotational part is divergence-free and the
divergent part is irrotational, or
v = v
ROT
+ v
DIV
with ∇·v
ROT
= 0, ∇×v
ROT
= 0
∇·v
DIV
= 0, ∇×v
DIV
= 0
(6.1)
From the rules of vector analysis we recognize that (6.1) is satisfied if
v
ROT
=∇×A, v
DIV
=−∇χ (6.2)
where A and χ are known as the vector potential and the scalar potential of v,
respectively. The minus sign in the second equation is conventional. Often the
scalar velocity potential is simply called the velocity potential.
The potentials A and χ are unknown quantities. For (6.2) to hold it is also
necessary that the divergence of the vector potential vanishes. The proof will be
given later. As a consequence of (6.2) we may write
v =∇×A −∇χ (6.3)
214

6.1 The three-dimensional Helmholtz theorem 215
To show that it is possible to split the vector v in this manner we take the divergence
and then the curl of (6.3) and find
∇
2
χ =−∇·v, ∇
2
A =−∇×v (6.4)
wherewehavemadeuseoftheassumption∇·A = 0. According to (M6.82) the
formal solutions of these two Poisson equations are given by
χ(r) =
1
4π
V
∇·v
|
r − r
|
dτ
, A(r) =
1
4π
V
∇×v
|
r − r
|
dτ
(6.5)
where we have replaced the unspecified function f (r
). With the help of (6.5),
provided that the divergence and the curl of the vector v are known, we may
calculate A and χ and then the vector v itself. The proof will be complete if we
can show that the divergence of the vector potential ∇·A vanishes.
It is immediately obvious that
∇
1
↓
r − r
=−∇
1
r −
↓
r
(6.6)
so that
∇·A(r) =−
1
4π
V
∇×v
·∇
1
r −
↓
r
dτ
(6.7)
Applying the vector rule B ·∇C =∇·(BC) −(∇·B)C, setting in (6.7) B =∇×v
and C = 1/
r −
↓
r
,weobtain
∇·A(r) =−
1
4π
V
∇·
∇×v
|
r − r
|
dτ
+
1
4π
V
1
|
r − r
|
∇·∇×v
dτ
=−
1
4π
S
∞
∇×v
|
r − r
|
· dS = 0
(6.8)
since ∇·∇×v
vanishes. As the last step we have applied the divergence theorem.
We have introduced a sufficiently large surface S
∞
since it was assumed that ∇×v
vanishes on approaching infinity.
From these results we conclude that, for irrotational stationary potential flow
∇×v = 0, the velocity is given by
v =−∇χ =⇒ ∇ · v =−∇
2
χ (6.9)
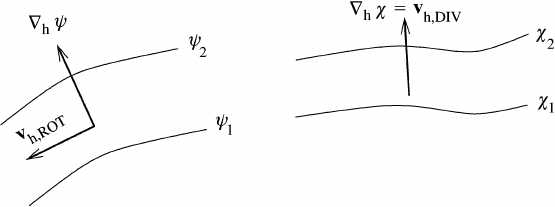
216 The Helmholtz theorem
Fig. 6.1 The stream function ψ and velocity potential χ.
As we have seen, if the divergence of the flow field is known, the velocity potential
can be calculated with the help of (6.5) if the region of integration is infinitely
large. In this case the boundary is undefined. In practical meteorology, in general,
the region has a finite boundary and equation (6.9) must be treated as an elliptic
boundary-value problem by specifying the velocity potential (the Dirichlet prob-
lem) or its normal gradient (the Neumann problem) on the boundary. The solution
is usually found by numerical methods. It is also possible in the case of a finite
boundary to proceed analytically. This leads to the introduction of Green’s function,
which often is difficult or even impossible to obtain since it depends on the shape
of the boundary. We will not broaden this topic since potential flow does not occur
in large-scale dynamics.
6.2 The two-dimensional Helmholtz theorem
The three-dimensional Helmholtz theorem has its two-dimensional counterpart.
Since the large-scale motion can often be approximated as two-dimensional flow
it is useful to consider the consequences of Helmholtz’s theorem. Instead of (6.1)
we now have
v
h
= v
h,ROT
+ v
h,DIV
∇
h
· v
h,ROT
= 0, k ·∇
h
× v
h,ROT
= 0
∇
h
· v
h,DIV
= 0, k ·∇
h
× v
h,DIV
= 0
(6.10)
From the rules of vector analysis we immediately recognize that
∇
h
· v
h,ROT
= 0ifv
h,ROT
= k ×∇
h
ψ
k ·∇
h
× v
h,DIV
= 0ifv
h,DIV
=∇
h
χ
(6.11)
This leads to the definition of the stream function ψ and the two-dimensional
velocity potential χ; see Figure 6.1.
The stream function should not be confused with the streamline, which can be
constructed for any type of flow, whereas the stream function results from the first
6.3 Problems 217
condition of (6.11). Using the relations (6.11) involving the stream function and
the velocity potential we may rewrite (6.10) as
v
h
= k ×∇
h
ψ +∇
h
χ (6.12a)
or in components
u =−
∂ψ
∂y
+
∂χ
∂x
,v=
∂ψ
∂x
+
∂χ
∂y
(6.12b)
Taking the vertical component of the curl and the divergence of v
h
, observing that
the curl of the gradient of the velocity potential vanishes, we obtain
k ·∇
h
× v
h
=∇
2
h
ψ = ζ =
∂v
∂x
−
∂u
∂y
∇
h
· v
h
=∇
2
h
χ = D =
∂u
∂x
+
∂v
∂y
(6.13)
By providing proper boundary conditions the Poisson equations for ψ and χ can
be solved. Moreover, solutions analogous to (6.5) can be written down. By suitable
differentiation of ζ and D in (6.13) with respect to x and y and adding (subtracting)
the resulting equations, we immediately find two additional Poisson equations for
the horizontal velocity components u and v:
∇
2
h
u =−
∂ζ
∂y
+
∂D
∂x
, ∇
2
h
v =
∂ζ
∂x
+
∂D
∂y
(6.14)
Equations (6.12)–(6.14) show the inter-relations among the horizontal velocity
components u, v, the stream function ψ, the velocity potential χ, the vorticity
ζ , and the divergence D. Finally, we would like to remark that it is possible to
generalize the stream-function method to three dimensions; see Sievers (1995).
6.3 Problems
6.1: Consider the three-dimensional velocity field defined by
v =−∇×Ψ +∇φ
Apply the condition ∇·Ψ = 0.
(a) Find the relations of (∇v)
I
, (∇v)
×
,and(∇v)
.
(b) Express the vortex equation
d
dt
∇×v =−(∇×v)(∇·v) + (∇×v) ·∇v −∇
1
ρ
×∇p
in terms of Ψ and φ.

7
Kinematics of two-dimensional flow
7.1 Atmospheric flow fields
In the previous chapter we have shown that the horizontal wind vector may be
decomposed into one part v
h,ROT
, which is divergence-free, and a second part
v
h,DIV
, which is irrotational. On the basis of this decomposition we will briefly
discuss various combinations of the flow field associated either with ∇
h
· v
h
= 0
and k ·∇
h
×v
h
= 0 or with the case in which the signs = and = are interchanged.
First of all, we consider the more general situation:
(i) ∇
h
· v
h
= 0andk ·∇
h
× v
h
= 0
In an atmospheric flow field whose characteristic length varies from roughly 50
to 2000 km, both parts, v
h,ROT
and v
h,DIV
, must be accounted for. In order to gain
qualitative insight into the structure of the fields of the stream function ψ and the
velocity potential χ, we assume a normal mode solution of the form
ψ
χ
∝ exp[i(k
x
+ k
y
+ ωt)] with k
x,y
=
2π
L
x,y
,ω= c
k
2
x
+ k
2
y
(7.1)
The quantity c is the phase velocity of the wave and k
x
and k
y
are the wavenumbers
corresponding to wavelengths L
x
and L
y
as shown in Figure 7.1.
We substitute (7.1) into the Poisson equations (6.13). Because of
∇
2
h
ψ
χ
∝−
k
2
x
+ k
2
y
ψ
χ
(7.2)
we obtain the qualitative statement
−
k
2
x
+ k
2
y
ψ
χ
∝
ζ
D
(7.3)
showing that the field of the stream function is characterized by the vorticity field
whereas the field of the velocity potential has the structure of the divergence field.
218

7.1 Atmospheric flow fields 219
Fig. 7.1 Propagation of a plane wave.
(ii) ∇
h
· v
h
= 0andk ·∇
h
× v
h
= 0
Now we will discuss some special situations. If the horizontal flow field is free
from divergence, Poisson’s equation for χ reduces to
∇
2
h
χ = 0(7.4)
which is Laplace’s equation for the velocity potential. A function with continuous
second derivatives satisfying Laplace’s equation is known as a harmonic function.
We may easily prove that a harmonic function within the region being considered
is zero if it is zero on its boundary. On multiplying (7.4) by χ and integrating over
the surface of interest, we find
S
χ∇
2
h
χdS
=
S
∇
h
· (χ∇
h
χ) dS
−
S
(∇
h
χ)
2
dS
= 0(7.5)
Application of Gauss’ two-dimensional integration theorem (M6.34) to the first
term on the right-hand side of (7.5) shows that this term is zero if we assume that
χ = 0 on the boundary of the region, or
S
∇
h
· (χ ∇
h
χ) dS
=
L
χ ∇
h
χ · ds
⊥
= 0(7.6)
where ds
⊥
takes the places of dr
N
. The second term of (7.5) is positive definite
so that ∇
h
χ = 0orχ = constant within the entire region of integration. Since
χ is zero on the boundary, the constant must be zero also. Therefore, the general
statement (6.12) reduces to
v
h
= k ×∇
h
ψ or u =−
∂ψ
∂y
,v=
∂ψ
∂x
(7.7)

220 Kinematics of two-dimensional flow
so that the velocity may be described solely in terms of the stream function ψ.For
large-scale atmospheric flow fields exceeding a characteristic length scale of about
2000 km, the divergent part of the velocity may often be disregarded. The flow
then follows the lines representing the constant stream function.
(iii) ∇
h
· v
h
= 0andk ·∇
h
× v
h
= 0
In the case that the rotation vanishes, we find from (6.13) the Laplace equation
∇
2
h
ψ = 0(7.8)
Repeating the argument of case (ii), we may conclude that ψ = 0. This is the
situation of purely potential flow as expressed by
v
h
=∇
h
χ, ∇
2
h
χ = D (7.9)
This type of flow is applicable to small-scale atmospheric motion such as mountain-
valley winds and land–sea breezes whose characteristic length scale is usually less
than 50 km. The essential difference from large-scale motion is that the Coriolis
effect is of minor importance. In the absence of centripetal forces the motion follows
the negative pressure gradient from high to low pressure but along the positive
gradient of the velocity potential. In the so-called fine structure of the pressure field
a minimum value of p is associated with a maximum of χ and vice versa.
(iv) ∇
h
· v
h
= 0andk ·∇
h
× v
h
= 0
In this case it is possible to equate the horizontal velocities according to (7.7) and
(7.9) to give
∇
h
χ = k ×∇
h
ψ (7.10)
or, in component form,
u =
∂χ
∂x
=−
∂ψ
∂y
,v=
∂χ
∂y
=
∂ψ
∂x
(7.11)
These are the famous Cauchy–Riemann equations from complex-variable theory,
which are rarely satisfied for atmospheric conditions. Nevertheless, these conditions
provide a perfect example of purely deformational flow.
As an exercise we will obtain the distributions of the stream function and the
velocity potential for the simple flow field described by
u = λx, v =−λy (7.12)
